矿用通风机叶片线激光测量数据优化方法研究

2024-04-19李学哲王彦昕花忠旭田文宇

计量学报 2024年3期

李学哲, 申瑶, 曹艾, 王彦昕, 花忠旭, 田文宇

(华北科技学院应急装备学院河北省矿山设备安全监测重点实验室，河北三河 065201)

1 引言

矿用通风机是煤矿生产的重要机电装备,叶片是其关键机械零件,叶片的几何形状和尺寸对通风机性能和安全稳定具有重要作用[1]。因此,矿用通风机叶片精确、高效测量显得尤为重要。

近年来,激光测量技术因为其非接触、高效率等特点成为叶片测量研究的热点。王帆等搭建了基于激光位移传感器的航空叶片型面快速测量平台,实现了叶片的高效自动化测量[2];刘博文等提出基于多个线激光传感器的叶片轮廓快速测量方法,测量精度达到30 μm量级[3];宋俊芳等利用激光干涉仪对叶片型面坐标测量机的几何误差进行标定,并建立误差综合补偿模型,有效提高系统的坐标测量精度[4];孙彬等提出一个倾角误差补偿的量化数学模型,有效补偿了物面倾斜对测量结果的影响[5];李昱坤等对线激光传感器的静态性能进行研究分析,总结了传感器稳定性、重复性和线性度的定性规律[6]。目前的研究主要针对航空发动机叶片,相关研究成果促进了航空叶片激光测量技术的进步,同时也为矿用通风机叶片激光测量提供了借鉴和参考[7]。

然而,矿用通风机叶片测量有其内在独特性,航空叶片测量方法并不完全适用。矿用通风机叶片工作条件恶劣,在实际测量中极易受到粉尘、油污等多种因素影响,激光测量数据往往存在误差和噪声,因此对激光测量数据进行优化处理,提高测量精度和效率,成为当前矿用通风机叶片线激光测量研究的重点。

本文从原始测量数据滤波和测量模型精准构建两个方面,研究一种基于数据优化的矿用通风机叶片线激光测量精度提升方法。考虑到煤矿井下环境恶劣、干扰严重等问题,采用卡尔曼滤波算法对原始数据进行降噪处理,基于最小二乘准则优选出适合通风机叶片几何特征的精确测量模型,从而为矿用通风机叶片线激光精密测量提供一种有效的技术解决方案。

2 矿用通风机叶片线激光测量系统

为了检测矿用通风机叶片的几何状态,精确评估叶片的变形程度,本文研究一种基于线激光技术的非接触式叶片几何测量系统。如图1所示,系统由三角测量支架、四自由度姿态调整机构、2D激光传感器、测试分析计算机、被测叶片等组成。其中,三角测量支架负责2D激光传感器与被测叶片之间位置关系初步调整,确保传感器能够采集到清晰完整的叶型轮廓曲线;四自由度姿态调整机构,通过高低、前后、俯仰、偏摆等4个自由度的灵活调整,实现测量剖面和测量姿态的优化选择,本研究中,测量剖面设置在叶尖以下5 mm处,传感器工作距离调整为100 mm;2D激光传感器负责测量剖面的高精度坐标采集,利用线激光投射于被测叶片检验剖面,一次采样可以获得二维坐标信息,具有非接触、高效率等技术特点;测试分析计算机上运行专用的测量分析软件,负责测量数据采集、数据预处理、测量模型提取、参数计算等。

图1 矿用通风机叶片线激光测量系统Fig.1 2D laser measurement system of the mining ventilator blades

2D激光传感器是测量的核心,选用如图2所示的LS-100CN激光传感器设计,该传感器基于线激光测量原理工作,内置图像处理算法,实现轮廓自动补偿,具有非接触、高精度、高效率、稳定可靠、宽动态范围等技术特点[8],其详细技术参数见表1。

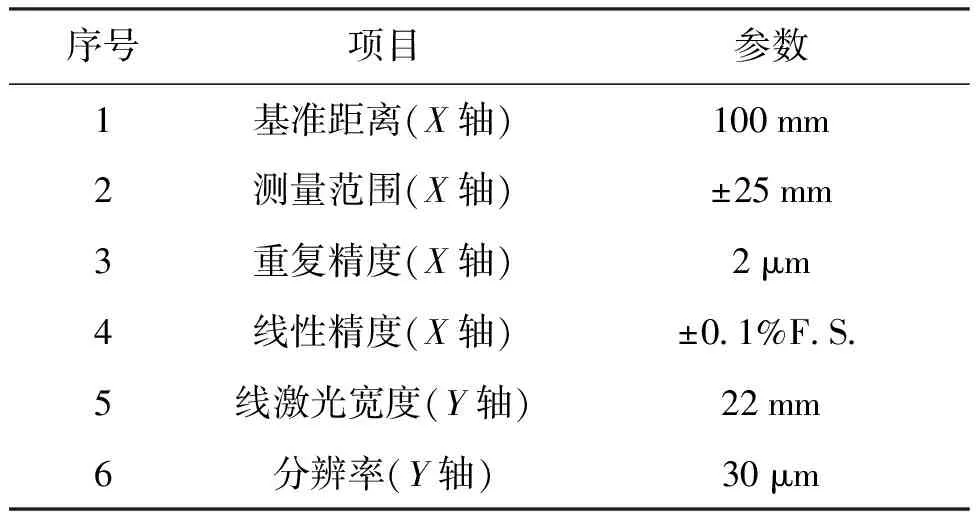
表1 LS-100CN激光传感器技术参数Tab.1 Technical parameters of LS-100CN laser sensor

图2 LS-100CN激光传感器Fig.2 LS-100CN laser sensor

系统采用2D激光传感器采集被测叶片表面的二维坐标数据信息,利用卡尔曼滤波算法对采集数据进行预处理,最后提取测量模型、参数计算,实现通风机叶片几何检测与评估。提高原始坐标数据和测量模型的精度,是测量的关键问题。

3 原始测量数据精度提升方法

3.1 线激光测量的误差分析

煤炭行业相关标准规定,矿用通风机叶片几何测量的仪器精度要小于50 μm[9]。如图3所示,影响线激光测量的误差因素很多,仪器自身的制造质量和精度、测量原理和方法误差、环境因素的变化、目标对象的表面光学性质、数据处理算法等对测量结果有较大影响。随着技术的发展和研究的深入,线激光测量的精度不断提高,目前市场上已经可以采购到精度水平达到10 μm量级的成熟商用产品,其误差在矿用通风机叶片测量允许的范围内,应该说,在使用方法得当的情况下,线激光测量技术完全可以满足通风机叶片测量的精度需求。

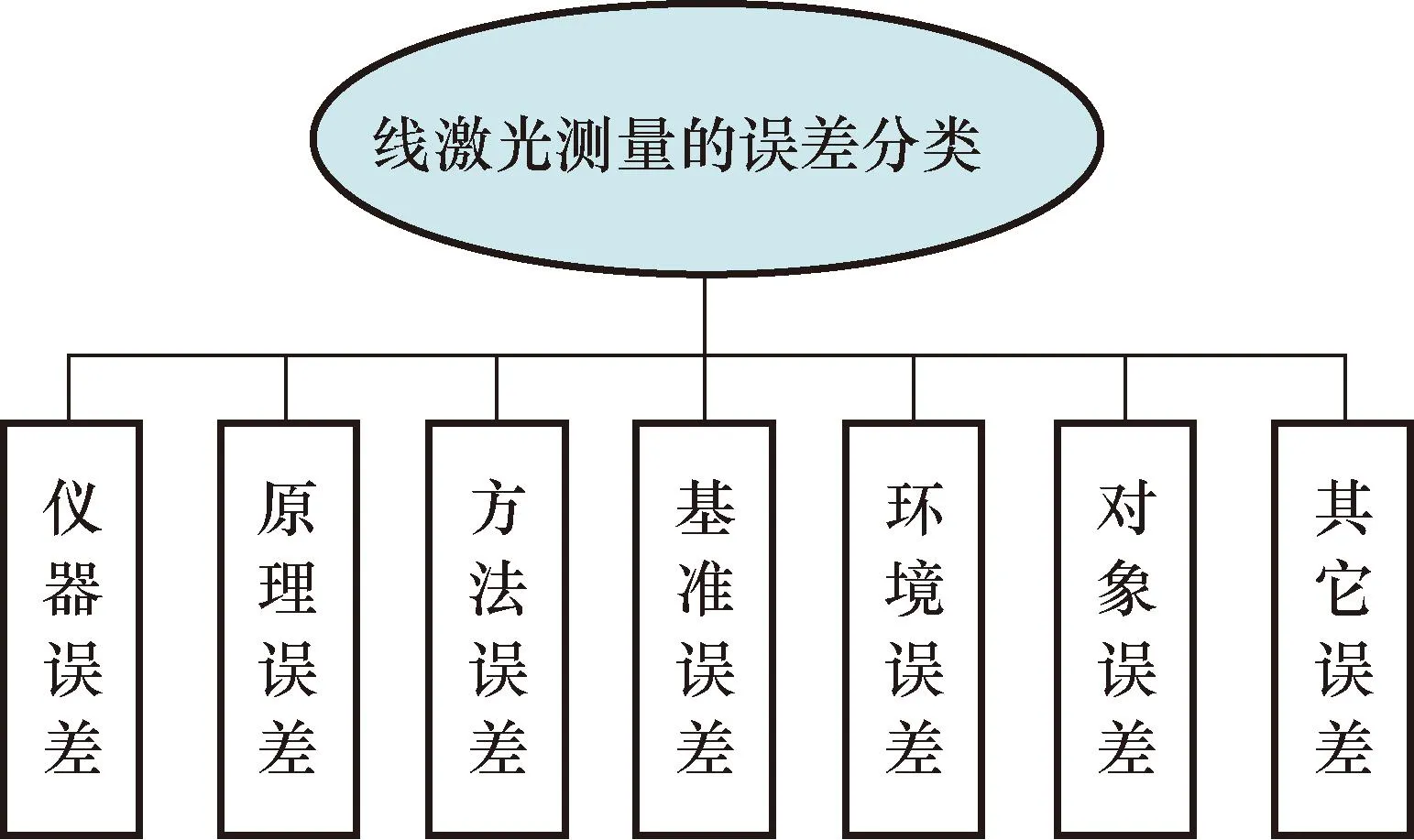
图3 线激光测量的误差分类Fig.3 Error classification of line laser measurement

但是测量数据在传输过程中,随机干扰是不可避免的,而且被测目标表面的斑痕、污渍等也会带来测量结果的波动,由于这些客观因素的影响,原始测量数据必须进行预处理,消除干扰因素,才可以应用于叶片几何分析[10]。本文采用卡尔曼滤波方法,解决这一问题,进一步提高坐标数据的测量精度。

3.2 基于Kalman滤波的数据优选方法

Kalman滤波是一种用于系统状态动态估计的数学方法,它能够处理包含噪声和不确定性的测量数据,是最佳估计领域的重要成果。Kalman滤波采用易于计算求解的递推形式,数据不必大量存储,可以逐一实时处理,特别适合于传感器测量数据实时处理与参数最优估计[11]。

如图4所示,Kalman滤波算法包括两个基本过程:预测和更新。预测阶段,利用线性系统模型和高斯噪声模型,根据上一时刻的系统状态最优估计值来预测当前时刻的状态,得到当前时刻的系统状态预测估计值和系统方差预测估计值;更新阶段,根据系统方差预测估计值和测量方差,融合求解卡尔曼滤波增益系数,结合当前时刻测量值改进预测阶段的系统状态预测估计值,更新得到当前时刻系统状态最优估计值[12]。

图4 Kalman滤波算法原理Fig.4 Principle of Kalman filtering algorithm

设系统状态方程(1)和观测方程(2)数学定义如下:

xk+1=Axk+Buk+rk

(1)

yk+1=Hxk+1+sk+1

(2)

式中:xk表示k时刻的系统状态向量;uk表示k时刻对系统的控制量;A和B分别表示从k时刻到k+1时刻的系统状态转移矩阵和系统控制矩阵;yk表示k时刻的观测向量;H表示系统预测输出转移矩阵;rk和sk表示状态和测量的噪声。

则Kalman滤波预测模型为:

(3)

(4)

Kalman滤波更新模型为:

(5)

(6)

(7)

式(5)用于卡尔曼滤波增益计算;式(6)用于对当前时刻系统状态量进行更新估计;式(7)用于更新计算当前时刻协方差最优估计值;R是测量噪声方差。

基于数学模型(1)～(7),设计Kalman滤波程序,利用该程序实时处理传感器原始数据,有效滤除信号中的噪声干扰,提高坐标测量的精度。

4 基于最小二乘准则的测量模型优化方法

基于离散数据提取测量模型的方法很多,其中高次多项式拟合法、B样条拟合法、贝塞尔拟合法最为常用。本文采用3种方法处理测量数据,分别拟合求解3个测量模型,并基于最小二乘准则评价各模型的精度,从而优选出适合通风机叶片几何特征的测量模型,为后续通风机叶片几何评价奠定基础。测量模型优化流程如图5所示。

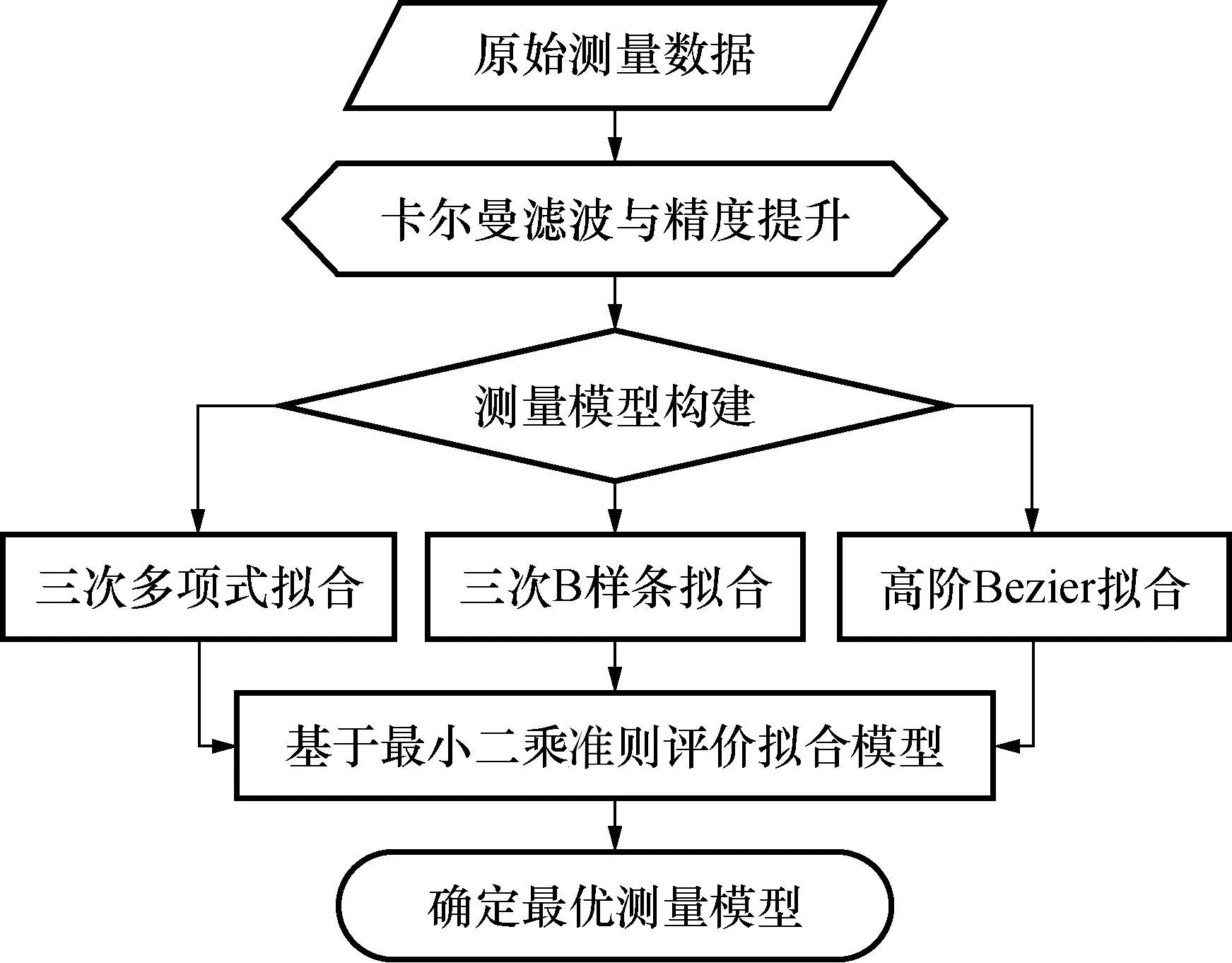
图5 基于最小二乘准则的测量模型优化流程图Fig.5 Flow chart of measurement model optimization based on least squares principle

4.1 三次多项式拟合法

考虑到通风机叶片的制造精度,一般可采用三次多项式函数拟合求解其测量模型。根据泰勒定理[13],三次多项式拟合曲线为:

y=f(x)=k3x3+k2x2+k1x+k0

(8)

设离散测量数据为(xi,yi),其中i=1,2,…,700,根据最小二乘法原理,如式(9)所示,拟合目标为偏差平方和达到最小:

(9)

将测量坐标代入式(8),得到方程组的增广矩阵,进而通过消元获得三次多项式函数的模型系数k0～k3。三次多项式拟合算法流程如图6所示。

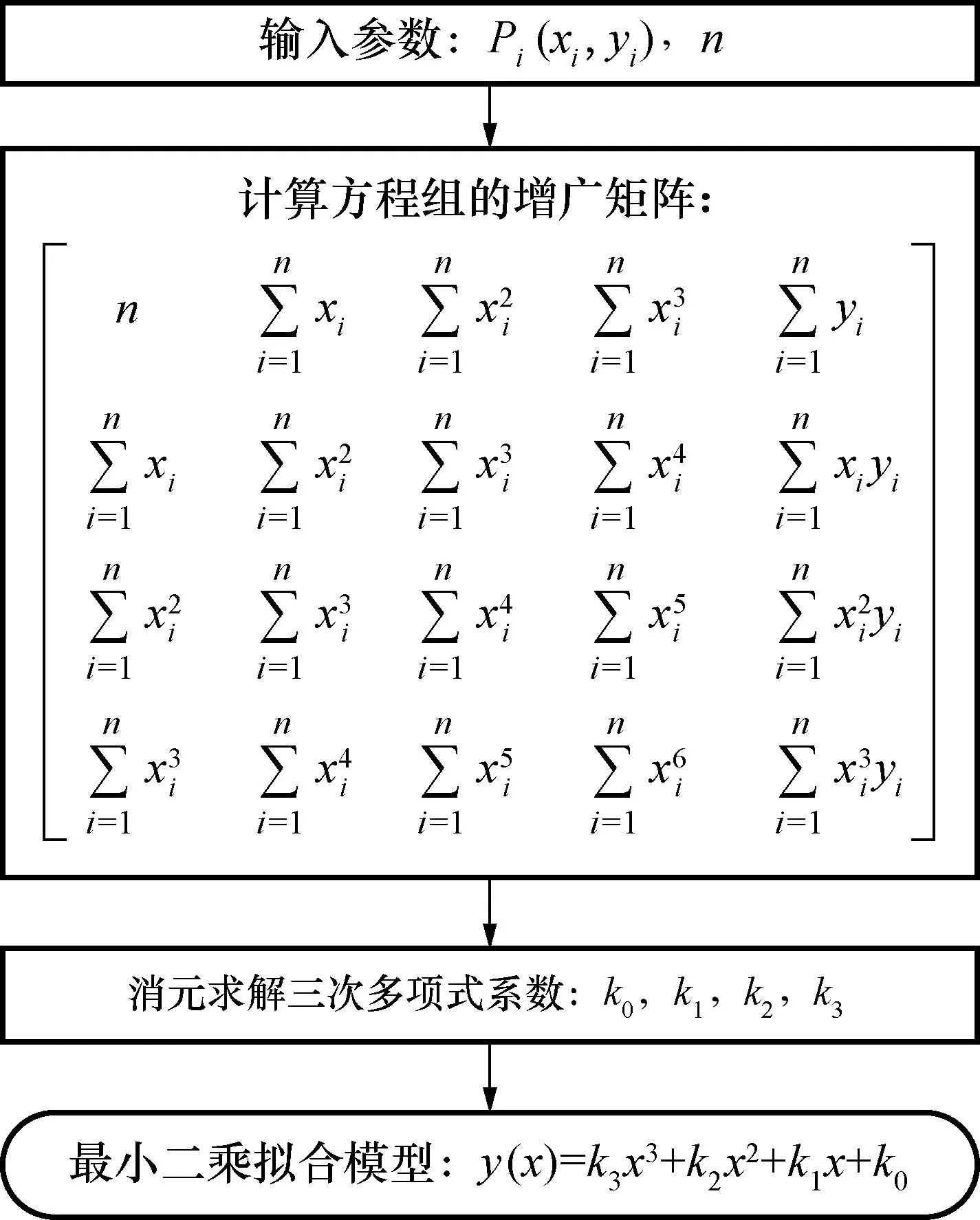
图6 三次多项式最小二乘拟合算法流程图Fig.6 Flow chart of least squares fitting algorithm for the cubic polynomial

4.2 三次B样条曲线拟合法

B样条曲线具有较好的局部性和连续性,本研究选用三次B样条模型对测量数据进行处理分析。三次B样条曲线方程表达式[14]如下所示:

(10)

(11)

(12)

式(10)中:Pi(i=0,1,2,3)为B样条曲线的控制点;节点矢量记为U=[u0,u1,ui];Ni,p(u)为第i个三次B样条基函数,该递推公式也称为Cox-de Boor递归公式,具体见式(11)、式(12)。

为了方便计算,三次B样条曲线方程也可采用矩阵表达式:

(13)

4.3 高阶贝塞尔曲线拟合法

贝塞尔曲线是基于伯恩斯坦多项式的样条曲线,m阶贝塞尔曲线由m+1个控制点控制[15]。m阶贝塞尔曲线数学表达式如式(14)所示:

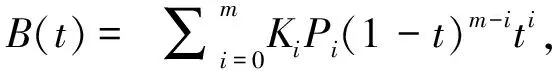
(14)

4.4 基于最小二乘准则的测量模型评定方法

最小二乘法是一种通过实验数据按照残差平方和最小准则匹配对应的解析函数的数据分析方法[16]。本文将最小二乘准则应用于拟合模型评价,采用离散测量点与拟合模型对应点的残差均方根F作为评价因子,如果F越小,表明该测量模型显著水平较高,该模型更适合通风机叶片测量模型的提取。评价因子F的数学定义:

(15)

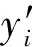
5 实验与分析

5.1 线激光测量与卡尔曼滤波实验

如图7所示,利用本文研究的线激光测量系统对某型矿用通风机目标叶片进行轮廓坐标数据采集,部分实验数据如表2所示,其中,XM、YM为采集的叶型原始测量坐标,XF、YF为卡尔曼滤波后得到的叶型最佳估计坐标。

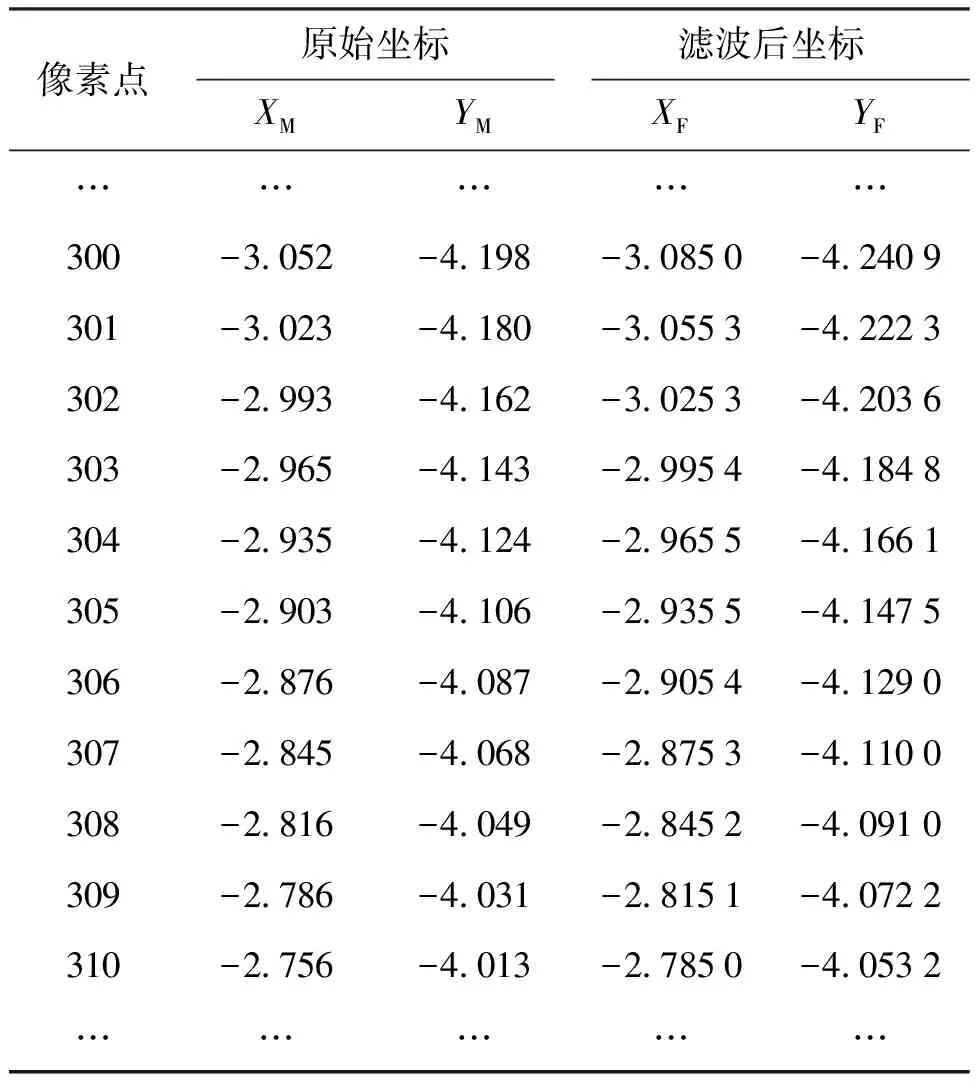
表2 目标叶片线激光测量数据

图7 矿用通风机叶片线激光测量实验图Fig.7 Experimental diagram of 2D laser measurement for the mining ventilator blades

图8为滤波前后的数据对比图.实验结果表明:卡尔曼滤波算法有效抑制了噪声干扰,滤波后数据波动减小,曲线更加平滑,为后续测量模型提取和参数计算提供了精准数据。

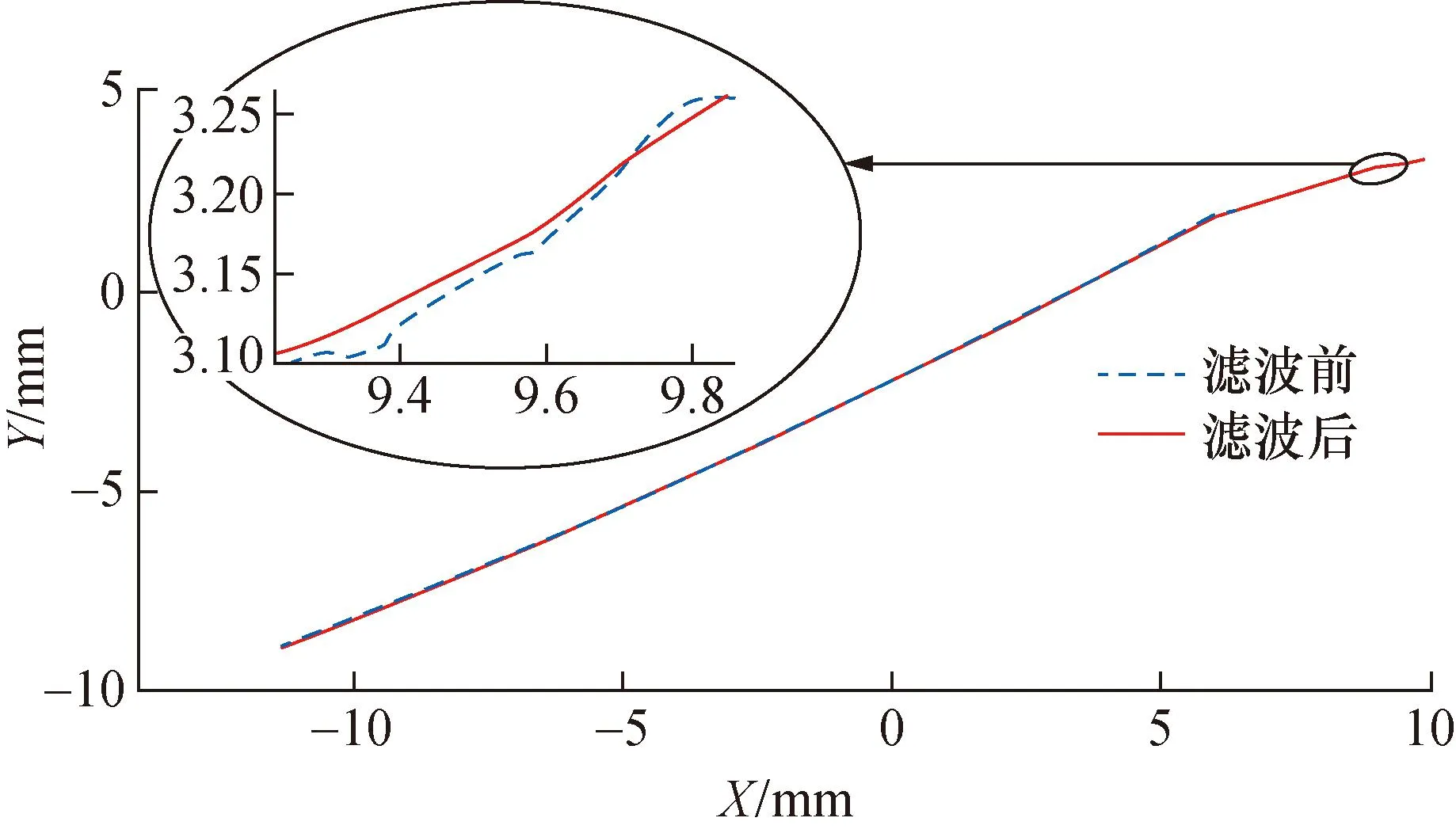
图8 滤波前后数据对比图Fig.8 Comparison of data before and after filtering

5.2 测量模型优化实验

基于滤波后离散的坐标数据,分别采用三次多项式、三次B样条和高阶贝塞尔函数构建叶片测量模型,得到如表3所示的实验数据,测量模型曲线如图9所示。表3中,X0、Y0为卡尔曼滤波后的叶片测量数据,Y1为利用三次多项模型(式(16))离散得到的纵坐标,Y3为利用高阶贝塞尔模型(式(17))离散得到的纵坐标,式(16)、(17)由前文研究的拟合算法求解。Y2为利用三次B样条模型离散得到的纵坐标。

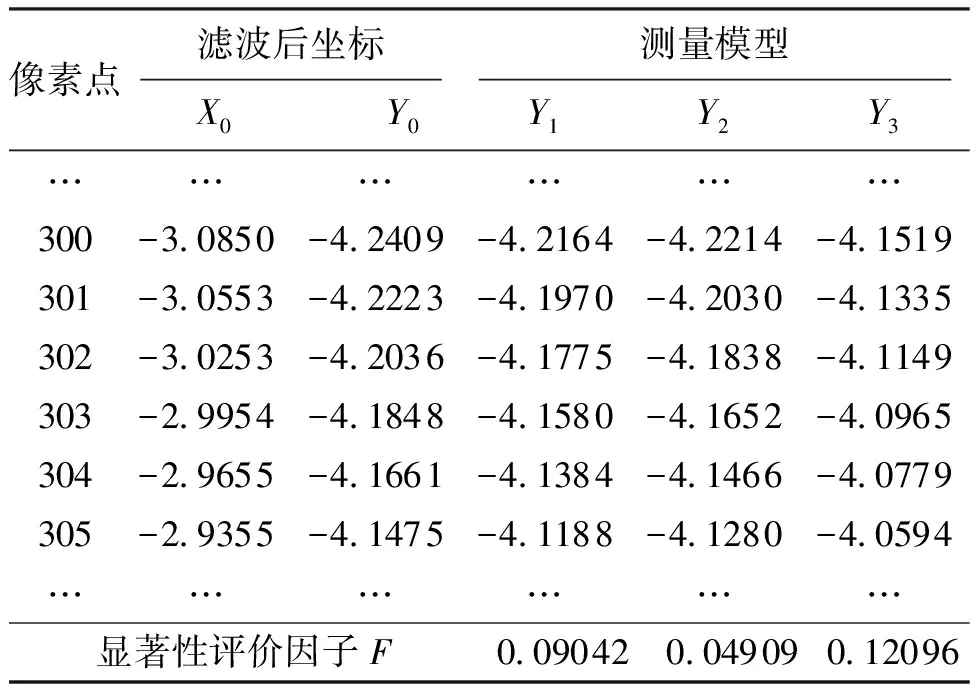
表3 叶片测量模型实验数据Tab.3 Model data of blade measurement mm

图9 叶片测量模型曲线Fig.9 Model curves of blade measurement

表3中,三次B样条模型的系数如表4所示。显著性评价因子F根据式(15)计算。计算结果表明三次B样条模型的评价因子最小,是最优的通风机叶片测量模型。

表4 三次B样条模型系数Tab.4 Coefficients of cubic B-spline model

Y1=-0.000 761X3-0.001 572X2

+0.664 6X-2.173

(16)

Y3=-1.004×10-10X7+2.616×10-10X6

-7.303×10-7X5-2.66×10-5X4

-4.806×10-4X3+8.018×10-4X2

+0.6341X-2.215

(17)

针对通风机叶片的几何特征,由图9可以得到如下结论:1) 由于采用分段拟合和控制点优化技术,三次B样条模型与测量数据的吻合度最高,是矿用通风机叶片的最优测量模型;2) 由于样本数量很大,三次多项式模型的精度优于贝塞尔模型,但低于三次B样条模型;3) 贝塞尔模型与测量数据的偏差最大,精度最低,不适合构建矿用通风机叶片测量模型。