基于曲面拟合的光学偏折系统显示屏标定方法

郭创为, 管钰晴, 沈瑶琼, 徐瑞书, 朱言瑧,刘丽琴, 张玉杰, 雷李华, 傅云霞

(1.上海市计量测试技术研究院，上海 201203； 2.上海市在线检测与控制技术重点实验室，上海 201203)

1 引 言

光学自由曲面能够针对性地矫正光学系统中的各类像差,是近年来光学系统设计领域的重要发展方向[1]。透射波前是衡量光学透镜是否符合设计和使用要求的重要指标,目前已有的自由曲面面形和波前测量方法往往不能同时兼顾测量精度、测量动态范围、使用成本以及适用性等多方面的需求[2～4]。透射式光学偏折术具有结构简单、检测精度高、动态检测范围大等优点,能很好地满足检测自由曲面透射波前面临的诸多限制条件[5,6]。

光学偏折系统中的标定误差是影响其最终波前测量精度的主要因素。系统标定和各部分组件的标定过程,均会引入一定的系统误差[7～9],透射式光学偏折系统的系统误差主要分为透镜的定位误差、CCD相机和显示屏的标定误差、整个系统的几何定位误差。高精度的系统结构标定、CCD相机和显示屏的内外参数标定,是高精度波前测量的关键。

当前针对透射式光学偏折系统的标定研究主要围绕相机的内外参数以及各组件定位误差展开[10]。Petz M等[11]受反射式条纹偏折术标定方法的启发,提出移动屏幕实现光线传播方向的追迹,将显示屏幕置于高精密位移台上,通过移动位移台改变屏幕位置,实现对系统参数的标定;Liu Y等[12]利用该标定模型,提出通过定位算法进行屏幕位置标定,该方法可以不受位移台精度影响,但由于显示器和相机都存在Gamma效应,所以标定精度不高。2007年,刘元坤等[6]提出了一种相位物体波前测量方法,通过移动显示屏,找到CCD相机上单个成像单元对应在两个不同位置显示屏中的发光像素点,这两个发光像素点发出的光线入射角不同,但出射光线重合,通过这种对发光像素点的位置标定,可计算出待测元件该点处的波前斜率,由波前斜率通过积分重建可反推波前,实现对波前的重构。2017年,姜丽丽[13]通过改进文献[6]中提出的方法,采用物方反投影误差对屏幕标定误差进行评价,对球面镜进行测量,结果显示波前像差测量精度(PV值)达到100 nm。

在透射式光学偏折系统的标定方法研究领域,缺乏对于显示屏面形标定误差的相关研究。由于显示屏表面形状形变受外力作用影响大,变形的显示屏会在透射式光学偏折系统中引入较大误差。

故本文针对显示屏幕面形对波前检测的影响展开具体研究。本文提出使用曲面拟合方法替代传统光学偏折系统中的平面标定方法。通过对屏幕进行曲面拟合,实现光学偏折系统中显示屏幕面形的高精度标定。通过仿真实验和波前测量实验,对传统平面拟合方式和所提曲面拟合方式的测量精度进行对比。结果显示:所提曲面拟合方式的测量精度明显优于传统平面拟合方式的测量精度,验证了曲面拟合显示屏面形标定方法的可行性。

2 透射式光学偏折术原理

透射式光学偏折术波前测量原理如图1所示,系统由LCD显示屏幕、具有针孔模型的CCD相机以及待测透镜组成[14]。LCD显示屏幕显示周期性正弦条纹,使用CCD相机拍摄不加待测透镜时的正常条纹图。加入待测透镜,光线经过透镜时会发生偏折而后进入CCD相机中,CCD采集到经过调制的形变条纹图[15,16]。通过使用相移法,投影同一周期不同时刻的多幅条纹图可完整记录相位信息。图1中,SK为不加待测透镜时的光线,SH为加入待测透镜后发生偏折的光线,通过进行高精度的标定工作和相位解算技术,可以确定CCD成像阵列上某一成像单元在待测透镜加入系统前后,该成像点对应在显示屏幕上的初始位置K和偏移位置H,以及对应的空间偏移量。

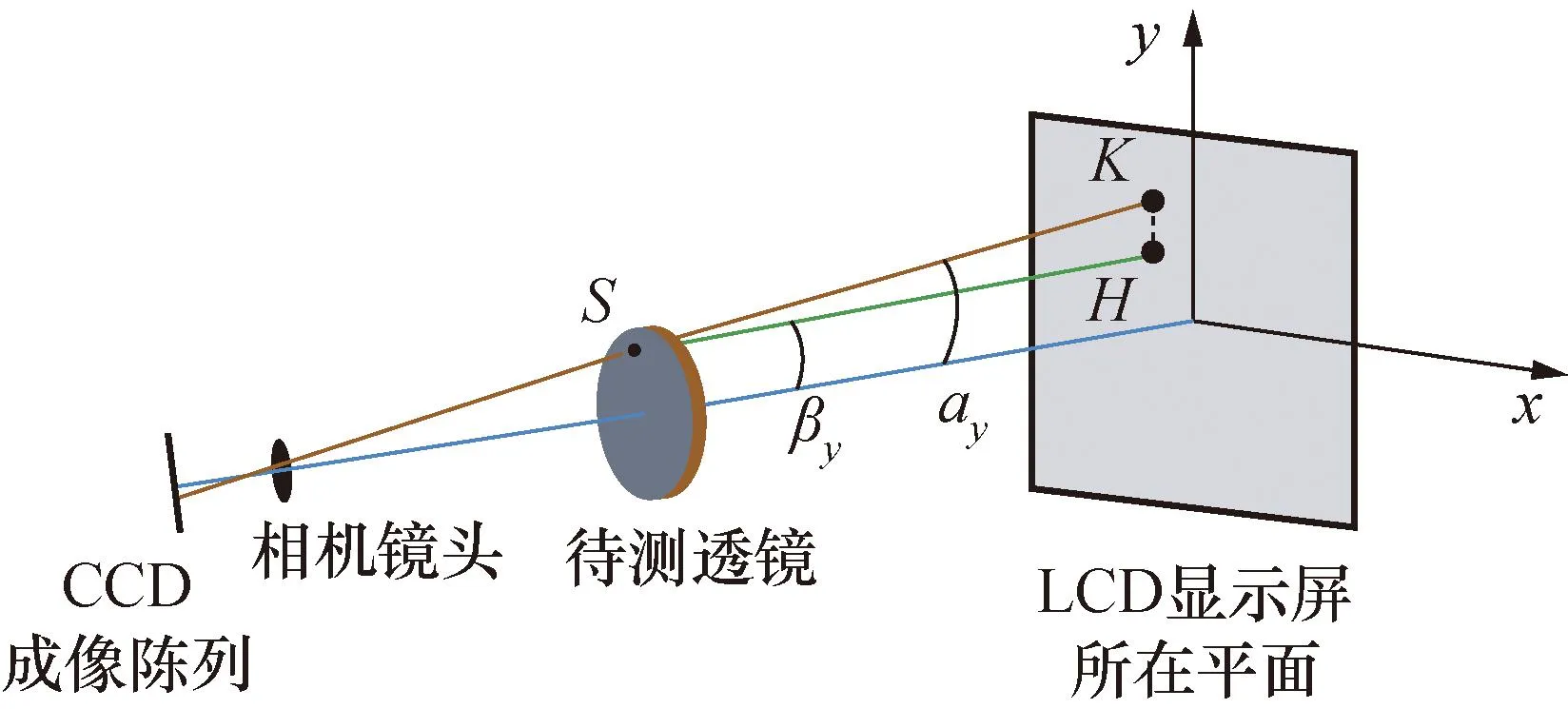
图1 透射式光学偏折术波前测量原理Fig.1 Wavefront measurement principle of transmission optical deflection technique

同理,也可求出显示屏上某一点加入透镜前后在CCD成像阵列上的像点[17]。对光线SK、SH分别在x、y轴作投影,在x方向的夹角分别为αx、βx,在y方向的夹角为αy、βy,由此可计算光线在x、y方向的偏折角度,分别为αx-βx,αy-βy,光线在x、y方向的偏折角度的正切值就是所求的波前斜率:

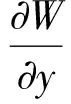
(1)

通过式(1)可以求解出各个点在x、y方向的波前斜率,再通过积分重建,可由波前斜率重建出待测透镜的波前信息。

3 屏幕面形标定

透射式光学偏折系统中,相机成像模型有4个基础坐标系,如图2所示,分别是世界坐标系(XW,YW,ZW)、像素坐标系(u,v)、图像坐标系(X,Y,Z)、相机坐标系(XC,YC,ZC)。以相机坐标系作为世界坐标系,可简化系统标定过程。

图2 相机成像模型各坐标系关系图Fig.2 Diagram of the relationship between coordinate systems of the camera imaging model

3.1 平面屏幕模型标定

屏幕的形状标定主要目的是使屏幕中的像素位置能够通过世界坐标系表示。本文采用四步相移法[18]获取图像相位,四步相移法采集同一正弦条纹4幅间隔时长为周期的图像,通过对4幅图像进行反正切计算得到包裹相位分布情况[19]。相位数据分布在每个像素点上,这就要求显示平面中每个发光像素点都能被相机识别到准确位置,确保四步相移投影过程中,CCD相机不会错误采集部分像素点的相位值。通过四步相移可解算出显示屏幕各发光像素点的二维坐标,相位φx、φy与像素点坐标关系:

(2)

式中Tx、Ty分别是显示屏投影的横向和竖向条纹的单个周期宽度。

假设屏幕不受外力影响,是一个理想平面,屏幕物理坐标系可用式(3)表示:

Ax+By+Cz+D=0

(3)

对式(3)中参数A、B、C、D设置初始值。使用针孔相机模型进行光线追迹,显示屏各像素点被CCD相机采集。在采集到的图像中,间隔一定距离选取数个像素点进行显示屏面形标定,这些像素点在相机坐标系中的坐标表示为(x1,y1,z1),相机中心点坐标表示为(x1(u0,v0),y1(u0,v0),z1(u0,v0))。通过像素点在成像阵列和在显示屏上的位置关系,可将显示屏上的像素点用相机坐标系表示。利用相位值和投影条纹表达式,通过设置的条纹参数值,可确定像素点在显示屏幕平面对应的坐标(x2,y2,z2)。像素点到相机中心和显示屏幕中心的距离可表示为式(4)[20],设定Dc(u,v)表示像素点到相机中心的距离,Ds(u,v)表示像素点到屏幕中心的距离,η1、η2、η3分别表述相机坐标系中x、y、z方向上像素点与中心点的距离的平方,ρ1、ρ2、ρ3分别表示图像坐标系中x、y、z方向上选取像素点与中心点的距离的平方,ε表示所有像素点Dc(u,v)与Ds(u,v)的范数距离的集合。计算Dc(u,v)、Ds(u,v)并使ε达到最小,可得方程参数A、B、C、D。

(4)

(5)

(6)

(7)

设C为1,根据式(4)～式(7)可以解得A=-0.338 41,B=-0.001 57,D=15.648。显示屏所在平面如图3所示。

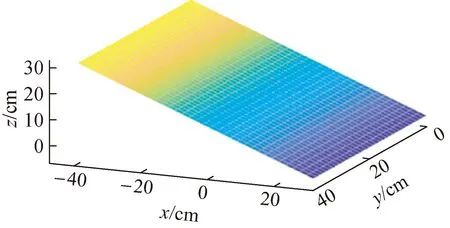
图3 显示屏所在平面Fig.3 Plane where the display screen is located

3.2 曲面屏幕拟合模型标定

由于显示屏幕的加工误差,以及屏幕出厂封装产生的压力,导致显示屏并不是一个相对理想的平面。其表面发生的弯曲会影响显示屏各个像素点的实际位置,使得屏幕上各像素点向世界坐标系转换时出现较大误差。故不能将屏幕当作理想平面看待,需要对屏幕引入曲面概念,采集点云图对其进行曲面拟合,得到其真实面形。

可通过三坐标测量机,对屏幕表面进行离散点取样。三坐标测量机的探针移动到被测点上,系统会自动显示并记录被测点的坐标值,而后通过将记录的各个离散点的坐标信息进行数据拟合得到其面形。

采用测量精度优于1 μm三坐标测量机对显示屏进行标定,对显示屏表面均匀采样,记录各采样点的三维坐标。

图4给出了拟合得到的曲面与标准平面之间的面形误差。

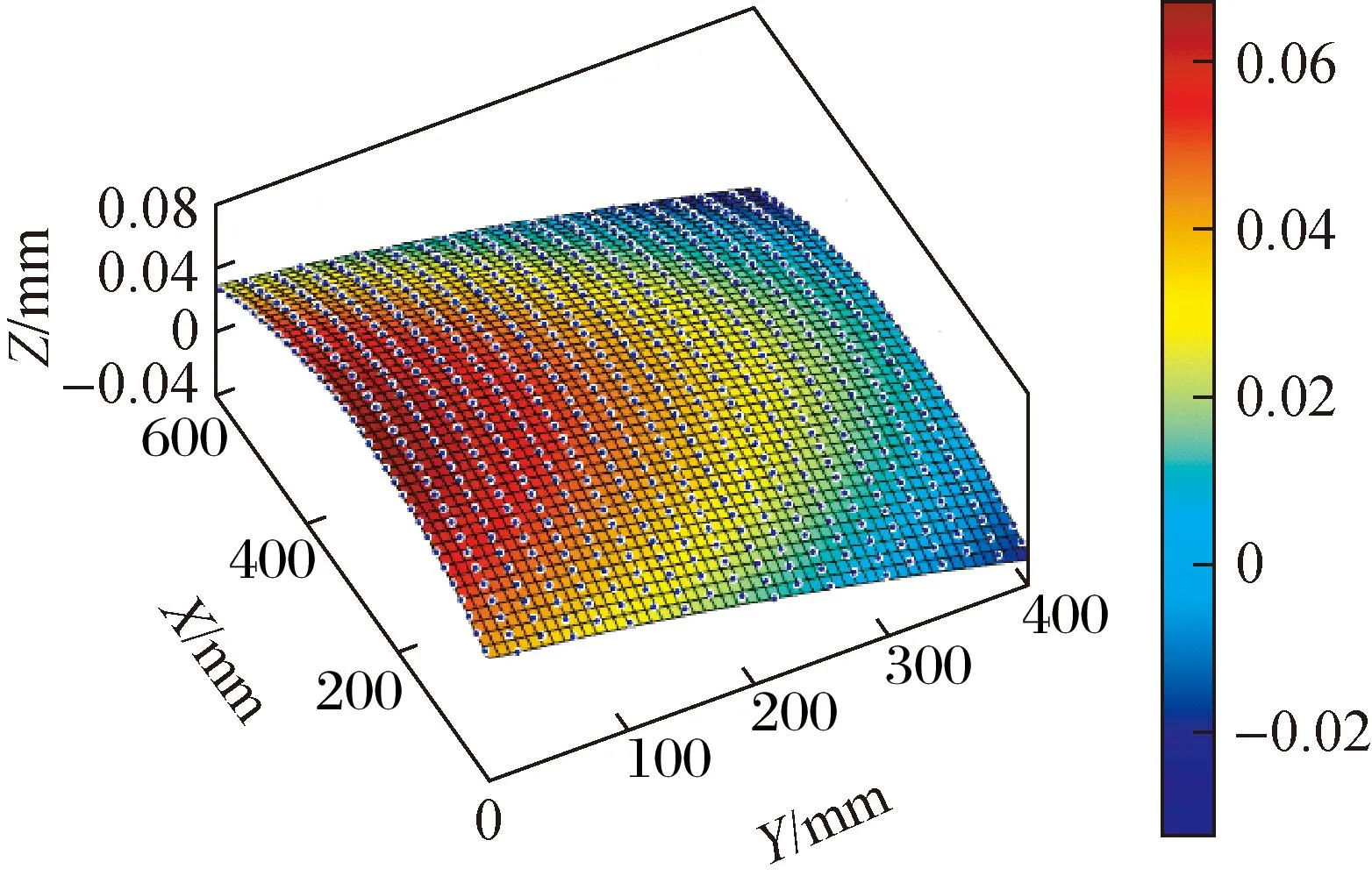
图4 显示屏曲面拟合误差结果Fig.4 Display screen surface fitting error results

面型误差拟合表达公式为

f=p00+p10x+p01y+p20x2+p11xy+

p02y2+p30x3+p21x2y+p12xy2+p03y3

(8)

表型拟合表达式中各参数数值见表1。

表1 面型拟合表达式中各参数数值Tab.1 The numerical values of each parameter in the surface fitting expression

4 显示屏面形拟合误差实验

4.1 显示屏面形拟合模型仿真

为了验证基于曲面拟合的透射式光学偏折系统显示屏标定方法的可行性,建立仿真模型,如图5所示。使用平面模型的显示屏幕和曲面模型的显示屏幕建立仿真实验系统,针对两种模型进行波前检测仿真实验,对曲率半径为80 mm,口径为30 mm的球面镜的透射波前进行仿真检测,待测透镜几何中心与像面之间的距离为110 mm。

图5 透射式光学偏折波前检测系统Fig.5 Transmission type optical deflection wavefront detection system

由已知球面透镜参数,在Zemax中生成透镜模型,得出透镜设计理想透射波前如图6所示,理想透射波前RMS=22.160 2 μm,PV=75.989 3 μm。图7为曲面和平面模型仿真波前图,从图7(a)可以看出曲面屏幕模型所测得波前与待测理想波前分布情况大致相同,图7(a)和图6中波前RMS值仅相差0.036 6 μm;对比图7(b)与图6,可以观察到所测透镜波前的左下部区域有明显变形,RMS差值达到0.437 2 μm。

图6 待测理想波前Fig.6 Ideal wavefront to be measured

图7 模型仿真波前Fig.7 Model simulation wavefront

为了更准确地观察不同面形屏幕模型测得波前的差异,分别计算两种模型仿真波前与理想波前的波前像差,见图8。曲面屏幕模型中波前像差RMS值仅为0.059 6 μm,平面屏幕模型波前像差RMS值则高达0.837 5 μm。对比图8(a)和图8(b),平面屏幕模型波前像差是曲面屏幕模型的14倍,且观察图8(b)波前像差分布情况可知,平面屏幕模型所测波前误差主要原因是显示屏幕所在平面水平方向存在弧度。

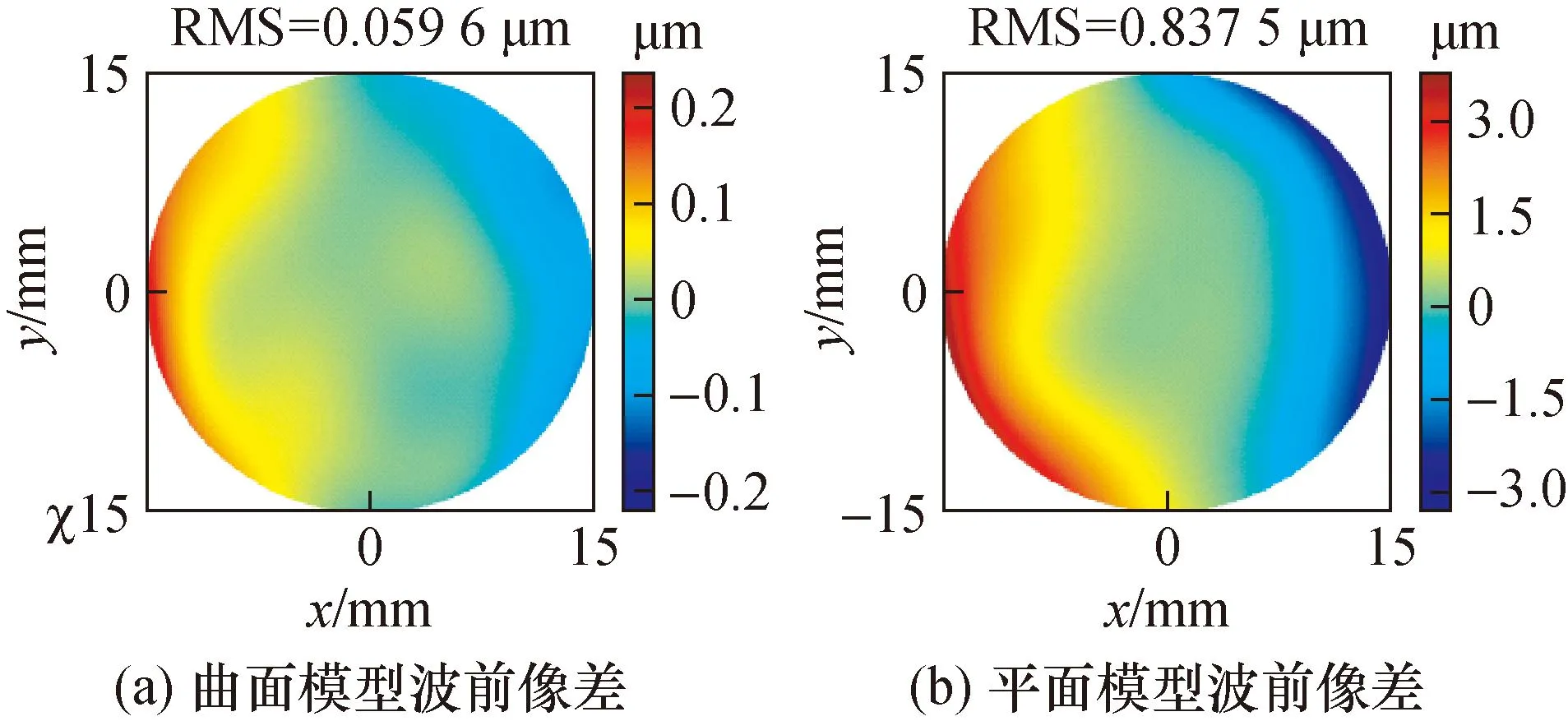
图8 不同模型测得的波前像差Fig.8 Wavefront aberrations measured by different models

针对图8中平面模型存在的较大残差值,导致此现象的直接原因是显示屏幕面形与平面模型与较大差异。分析其主要原因应为显示平面内部各位置元件几何属性不同,导致显示屏幕装配过程中内部各区域受力不均。部分区域由于内部压力过大,致使显示屏幕水平方向出现弧度,进而导致屏幕中像素点位置发生偏移。在实际系统搭建过程中应对显示屏幕面形进行曲面拟合,在整体系统中使用曲面显示屏模型代替传统的平面屏幕模型。

4.2 波前测量实验

本文搭建的透射式光学偏折术的波前检测系统由显示屏幕、CCD相机、待测透镜部分3部分组成,如图9所示,右侧为被测显示屏。本检测系统采用Basler ace2 a2A1920型CCD相机,水平/垂直像素个数为1 920×1 200,相机感光芯片尺寸6.6 mm×4.1 mm,水平/垂直像素尺寸3.45 μm×3.45 μm,最大帧速率160帧/s,相机镜头焦距 12 mm。显示屏幕为AOC公司21.5寸LED显示屏,像素分布为1 920×1 080,像素尺寸0.15 mm×0.15 mm。

图9 透射式波前测量系统Fig.9 Transmission type wavefront measurement system

本文搭建的透射式光学偏折系统对曲率半径为80 mm,口径为30 mm的球面镜的透射波前进行检测,待测透镜几何中心与像面之间的距离为97.386 mm,检测结果如图10所示。图10(a)为曲面屏幕模型波前检测结果,其RMS=22.233 7 μm;图10(b)为平面屏幕模型波前检测结果,其RMS=23.417 3 μm。

图10 球面透镜波前检测结果Fig.10 Wavefront detection results of spherical lens

去除透射波前中理想波前部分,得到透射波前像差,见图11。

图11 球面透镜波前像差图Fig.11 Spherical lens wavefront aberration diagram

曲面屏幕波前像差检测结果见图11(a),测得波前像差RMS=0.137 1 μm;平面屏幕波前像差检测结果见图11(b),测得波前像差RMS=1.432 6 μm,2种检测结果误差相差10倍。

5 结 论

本文提出使用曲面拟合方法替代传统光学偏折系统中的平面标定方法,使用三坐标测量机对屏幕表面进行均匀采点,对采样点进行曲面拟合实现光学偏折系统中显示屏幕面形的高精度标定。分别建立显示屏曲面拟合仿真模型和显示屏平面仿真模型,使用两种模型仿真测量球面镜波前。平面拟合仿真结果波前像差RMS值是曲面拟合仿真结果的14倍,证明理论上提出的显示屏曲面拟合方法的测量精度优于传统平面拟合效果。搭建了透射式光学偏折系统对球面镜进行透射波前测量。测量结果显示,采用曲面拟合标定的系统测得波前像差RMS=0.137 1 μm,平面拟合标定的系统测得波前像差RMS=1.432 6 μm。采用曲面拟合标定的系统测量效果明显优于平面标定的系统,证明了曲面拟合显示屏面形标定方法的可行性。

显示屏幕面形拟合不当会对系统造成较大误差,实际检测系统搭建和标定时应考虑显示屏幕因内部压力导致的面形弯曲,应采用曲面拟合的方式对显示屏幕面形进行拟合。