用于引力波探测的星间激光干涉测量模拟系统

穆衡霖, 李 岩

(清华大学 精密仪器系，北京 100084)

1 引 言

引力波在探索宇宙[1]的起源和演化中发挥着重要作用。受振动和重力梯度的影响,地面引力波干涉仪的敏感频段在10 Hz以上,而0.1 mHz～1 Hz频段蕴含着更丰富的宇宙信息的引力波则被淹没在噪声中。这些波段的引力波只能通过激光干涉空间天线(laser interferometer space antenna, LISA)、天琴(Tianqin)或者太极(Taiji)等臂长在106km量级的星间激光引力波干涉仪(inter-satellite laser interferometer, ISLI)进行探测[2～6]。

现有的ISLI均采用应答式干涉仪,这与传统的外差干涉仪有着显著的不同。探测引力波首先是在卫星1上发射W量级功率的稳频激光(主激光)传播106km后抵达卫星2,发散角使得接收的光功率仅在100 pW量级;而后,通过光学锁相环(optical phase-locked loop, OPLL)将卫星2上从激光的相位(频率)锁定到远处的主激光相位(频率)上;最后,卫星2上的激光再返回卫星1,两路光发生外差干涉,通过相位表分析相位变化,进而得到位移信号。

锁相环技术已经相当成熟,在弱光条件下,部分光学锁相环甚至能够达到散粒噪声极限[7～14]。然而,目前主流的光学锁相环都是模拟的,一旦失锁后难以自动锁定,在集成化和自动化上均不占据优势。相反,数字光学锁相环在兼容性、自动化和集成化等方面上具有显著优势,更适合应用在ISLI中,见文献[14]。

综合以上考量,本实验搭建了一套精度较高的星间激光干涉模拟系统,使用数字外差锁相环,成功将从激光器的相位紧密锁定到了主激光器(已稳频)的相位上。使用高精度相位表测量外差信号的相位,结果显示应答式干涉仪在长位移和短位移条件下均无粗大误差,而环境扰动和光路装调误差是主要噪声(误差)来源。实验中,主激光器的功率被衰减到100 pW量级,与ISLI中的弱光在同一数量级,证明了装置在外太空条件下的可行性。通过调整数字锁相环的参数改变主从激光的频率差,赋予了整个装置更大的灵活性。数字式锁相环与后续的数字信号处理电路相兼容,结合文献[13]中提出的自动锁定程序,可在一定程度上提高装置的自动化程度。

2 实验原理

图1是星间激光干涉测量模拟系统的结构图。主、从激光器均为Nd:YAG晶体的非平面环形腔激光器。整个实验系统的光学部分由稳频的主激光器(master laser),自由运转的从激光器(slave laser),声光移频器(acousto-optic modulator, AOM),光纤和光电探测器(detector)组成。而电学部分则包含相位表(phasemeter),PI控制系统(temperature control and PZT control),高电压放大器和射频驱动源(radio frequency, RF)等。装置的实物图如图2所示,主激光器上方的银白色仪器是执行锁相环和相位测量功能的关键电学仪器Moku: Pro,在实验中,整个装置被放置在亚克力罩子里。

图1 星间激光干涉测量模拟系统的示意图Fig.1 Structure diagram of inter-satellite laser interferometry simulation system

图2 主激光器(左)和从激光器(右)的照片Fig.2 Photos of the master laser (left) and slave laser (right)

光从主激光器出射,首先经过光隔离器和半波片后,进入偏振分光棱镜PBS,其s光(99%)反射而p光(1%)透射。p光用于稳频,而s光则作为测量光进入声光移频系统。

用于测量的s光首先经过普通分光棱镜BS后分为均等的两路,而后经过声光移频器AOM1和AOM2移频,两个移频器的移频量分别为f1=80 MHz和f2=82 MHz,用光阑滤去除+1级次之外的其他衍射级次,恰当使用光纤以减少反射镜,提高光路装配的灵活性(光纤以虚线表示)。

来自AOM1的光和从激光器经过AOM3的光合光,并被探测器Detector3感知。调节从激光器的温度,使得主、从激光的频率差在5～25 MHz内。随后,通过光学锁相环,将从激光器的频率锁定到主激光器经AOM1移频后的频率上。

与主激光器相似,从激光器出射的激光也经过光隔离器和半波片后,进入偏振分光棱镜PBS,其中s光(约1%)反射而p光透射。s光与来自主激光器经AOM1移频后的光合光并与用光学锁相环的搭建,而p光则传播至主激光器后,与主激光器经AOM2移频后的光合光,产生外差干涉信号。外差信号被探测器Detector2感知,经相位表后,分析得出其相位变化。在实际应用中,锁相环位置处产生误差信号的器件是相位表的一个通道, 而分析Detector2探测到的外差信号的是同一块相位表的另一个通道。此外,为了将光衰减到星间引力波干涉仪的功率水平,需要使用多个衰减片。图1中未对此做出明确描绘。

2.1 锁相环的搭建

探测器将主、从激光的外差信号转化为电信号,原始的交流外差电信号表达式为

(1)

(2)

式中:uACM(t)和uACS(t)分别表示主卫星和从卫星处的外差信号;RF=5 kΩ为光电探测器的反馈电阻;而R(λ0)=0.6 A/W是探测器的响应度;PM2和PS2分别表示主、从卫星上的本地强光功率;而PM1和PS1则表示弱光功率;fh=νM-νS是外差频率;φhm(t)=φm2(t)-φs1(t)和φhs(t)=φm1(t)-φs2(t)分别表示主、从卫星位置处的环外相位信息,忽略其他一切噪声和回路延迟时,两者是相等的。

原始的模拟电信号经前置低噪声放大器后,进入模数转换器并被数字化,随即输入相位表。相位表依赖于其内部的子锁相环工作,其详细工作原理见参考文献[15]。相位表给出输入外差信号和标准余弦信号(产生于数控振荡器)的相位差,并输出与此相位差成正比的电压信号(比例系数kI),再经过数字滤波器F(s)后,进入比例-积分反馈电路。控制器电路分为快伺服回路(控制压电陶瓷)和慢伺服回路(控制温度),压电陶瓷和温度的响应函数分别为P(s)和T(s),而控制器的传递函数则分别为CP(s)和CP(s)·CT(s)。经快慢两个回路后,最终从激光的频率与主激光的频率相差严格的fh,也就是从激光相位紧密锁定到主激光相位上。光学锁相环的传递函数如图3所示。

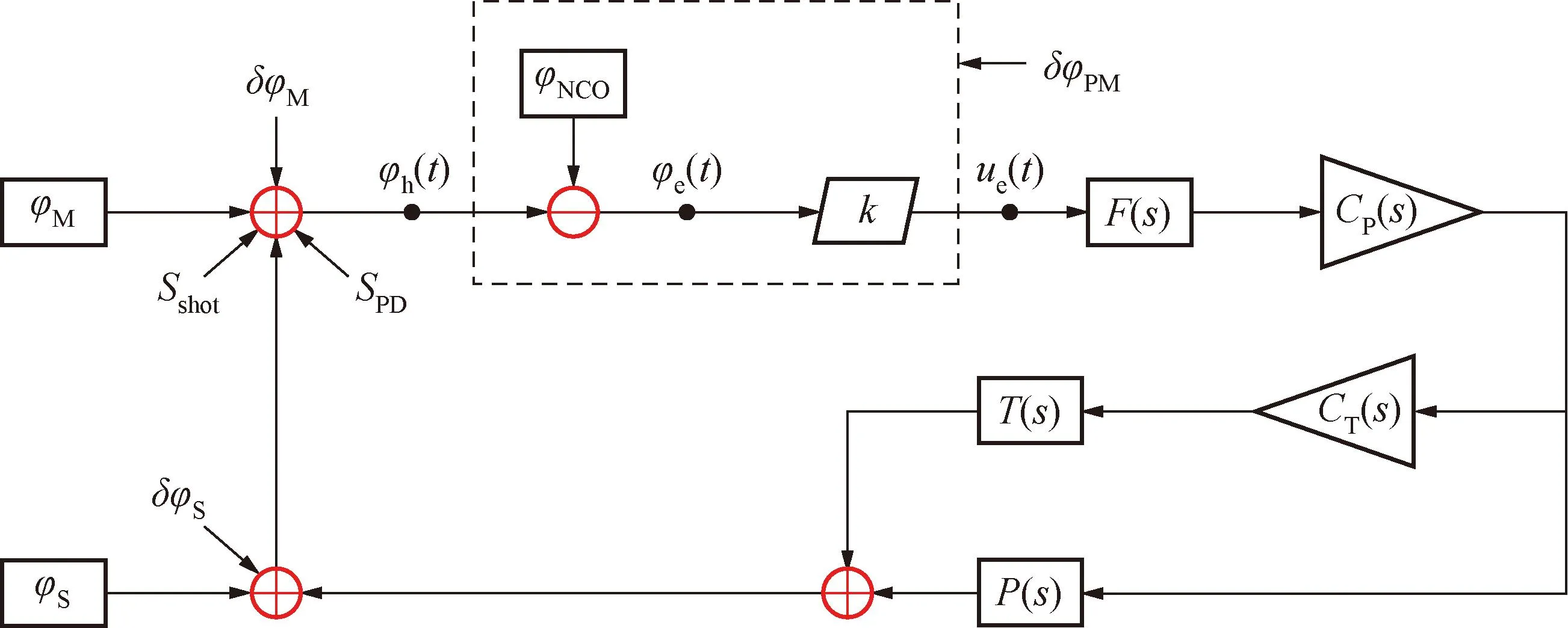
图3 光学锁相环的传递函数图Fig.3 Block diagram and the main noise sources of the OPLL

图3中,Sshot是散粒噪声,δφM是主激光相位噪声,δφS是从激光相位噪声,δφPM是相位表的相位噪声,SPD是探测器噪声。

经多次优化,数字式光学锁相环的传递函数分别为

(3)

(4)

(5)

而两个执行器件温度和压电陶瓷的传递函数则分别为

(6)

(7)

经分析,系统不存在s域右半平面的极点,因此整个系统具有稳定性。此外,尽管从公式(4)和公式(5)上看CP和CT在零频率处的响应是无穷大,但受限于仪器本身,这种响应必然是有限度的,这使得整个装置具有足够的相位裕度。

2.2 位移测量原理

当锁定完成时,如果主、从卫星发生相对运动(即位移台运动)时,设相对位移为ρ(t),根据多普勒效应,主卫星处探测器得到的外差信号相位将发生变化,进而可求得位移信号。理论上,忽略一切光程噪声,在Detector2处外差信号的相位为

(8)

式中:p(t)是主激光器的相位噪声;τrt是光的来回传播时间。

将解调频率选择为fh,则公式(8)中的第一项可被消去,那么理论上造成相位变化的就是位移和激光频率噪声。

激光频率噪声而引入的长度噪声为

(9)

式中:Sfrequency(f)是主激光的频率噪声;Sx(f)是长度噪声。

地面模拟装置体积较小(单次光程不足 30 cm),因此所带来的光传播时间极小,公式(9)即可近似为

(10)

当使用超稳激光器时,激光的频率噪声将不再是本实验中的主要噪声来源,这一点会在第3节中详细叙述。

根据公式(8)～公式(10),考虑到本实验中“主卫星”固定,那么“从卫星”的位移信号与主激光器相位信号的换算关系为

(11)

公式(11)与正常的外差干涉长度测量系统的结果是完全一致的,因此可以认为,从卫星或者说从激光器起到了“反射镜”的作用。

3 误差(噪声)测量

3.1 基本测试

在正式实验进行之前,首先测量主激光器的频率噪声。将主激光器与中国计量科学院(NIM)的超稳光频标激光器合光后,使用频率计测量拍频信号的频率,门时间设定为0.1 s,对信号做谱密度计算后,主激光器的频率噪声结果如图4所示。

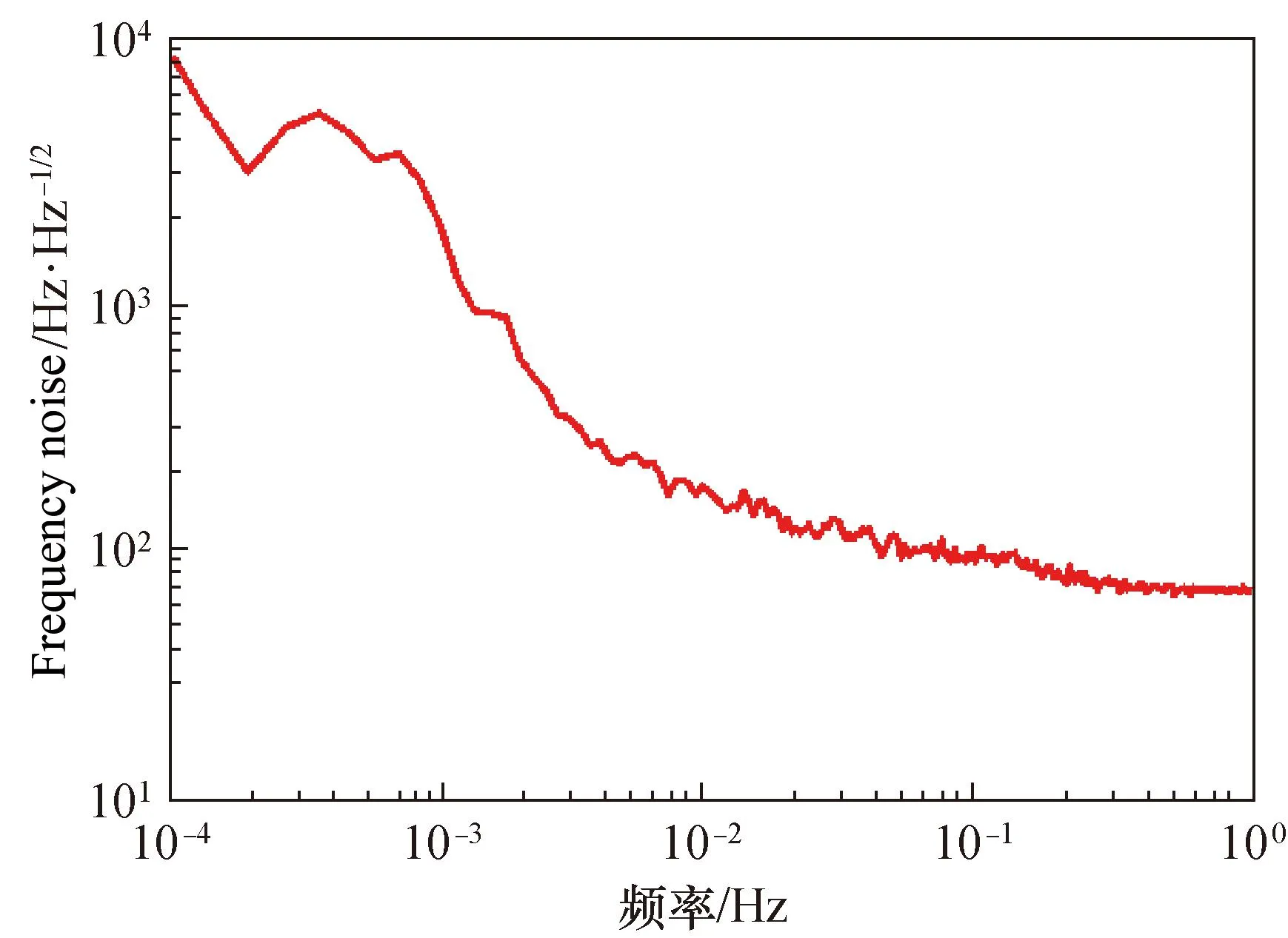
图4 主激光器的频率噪声Fig.4 The frequency noise of the master laser

根据图4,主激光器的频率噪声在10 mHz以下频段出现显著抬升,具有较为典型的1/f线型,根据参考文献[16],自由运转的非平面环形腔激光器的频率噪声可以建模为

(12)

稳频过程将激光的频率噪声压缩了约4个数量级。

相位表是产生误差信号的器件,其鉴相噪声基底决定了系统的相位噪声基底。将标准铷钟的信号分成2路,分别接入相位表的两个输入接口内(相位表可同时测量两路信号),理论上讲,两路信号完全相同,这时相位表输出两路信号的差值就可作为相位表的噪声基底。经测量,差值相位信号的振幅谱密度函数(amplitude spectral density, ASD)如图5所示。

图5 相位表的噪声基底(幅度谱密度)Fig.5 Noise floor of the phasemeter

3.2 零漂测试

首先,固定所有光学元件,读取detector3上外差信号的零漂。在这里,弱光功率在100 pW量级,而强光功率约0.5 mW。测量约6 h的零漂数据并对时域信号做谱密度分析,得到长时间零漂测试结果如图6所示。

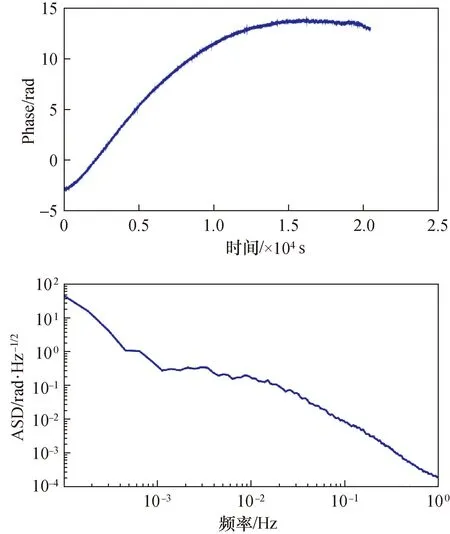
图6 长时间零漂测试Fig.6 Zero drift during a very long time

在图6中可以看到,随着时间的推移,零漂出现显著变化,总共漂移了约17 rad。考虑到实验时间约为11:00～17:00,可以认为这种变化主要来自于环境温度和气压带来的折射率变化,未来将装置置于真空中,能有效抑制零漂。

从长时间零漂的结果看,整个频谱图具有典型的1/f线型。在较高频段(0.03～1 Hz),零漂的谱密度低于0.06 rad/Hz1/2,换算到长度小于10 nm/Hz1/2,可以认为具有较低的噪声水平。但是,在更低的频段,例如0.1 mHz附近,谱密度超过40 rad/Hz1/2,因环境缓慢变化带来的低频段的漂移十分显著。因此,本装置的有效频段主要位于高频段,也就是0.03～1 Hz,尤其是0.1～1 Hz。

从频段上看,ISLI重点关注0.1 mHz～1 Hz频段,本实验中的锁定时间能超过2×104s,且直到采集数据结束时仍无失锁迹象,因此具有探测该频段的基本能力。可根据此地面模拟干涉仪的一系列表现来研究诸如“太极”计划(敏感频段恰好也为0.1 mHz～1 Hz)等天基引力波干涉仪的噪声,见文献[6]。

同时,根据公式(10),激光频率噪声带来的鉴相噪声为

Sφ(f)=πτrtSfrequency(f)

(13)

因此,即便是在频率噪声最大的低频段,激光的频率噪声对零漂的影响也不足2×10-4rad/Hz1/2,显然不是零漂的关键影响因素。然而,在实际的星间激光干涉中,对于百万公里量级的不等臂长,激光频率噪声的影响将是显著的,见文献[16]。

3.3 长位移测试

为测试干涉仪的表现,在锁定完成后,驱动位移台,观察相位表示数。在这里,弱光信号被设定为200 pW以下,强光信号则根据情况而调整。在较长时间内,令位移台以固定速度0.25 mm/s做往复运动(调转方向的时间已考虑在内),单次运动的行程为100 mm,其结果如图7所示。

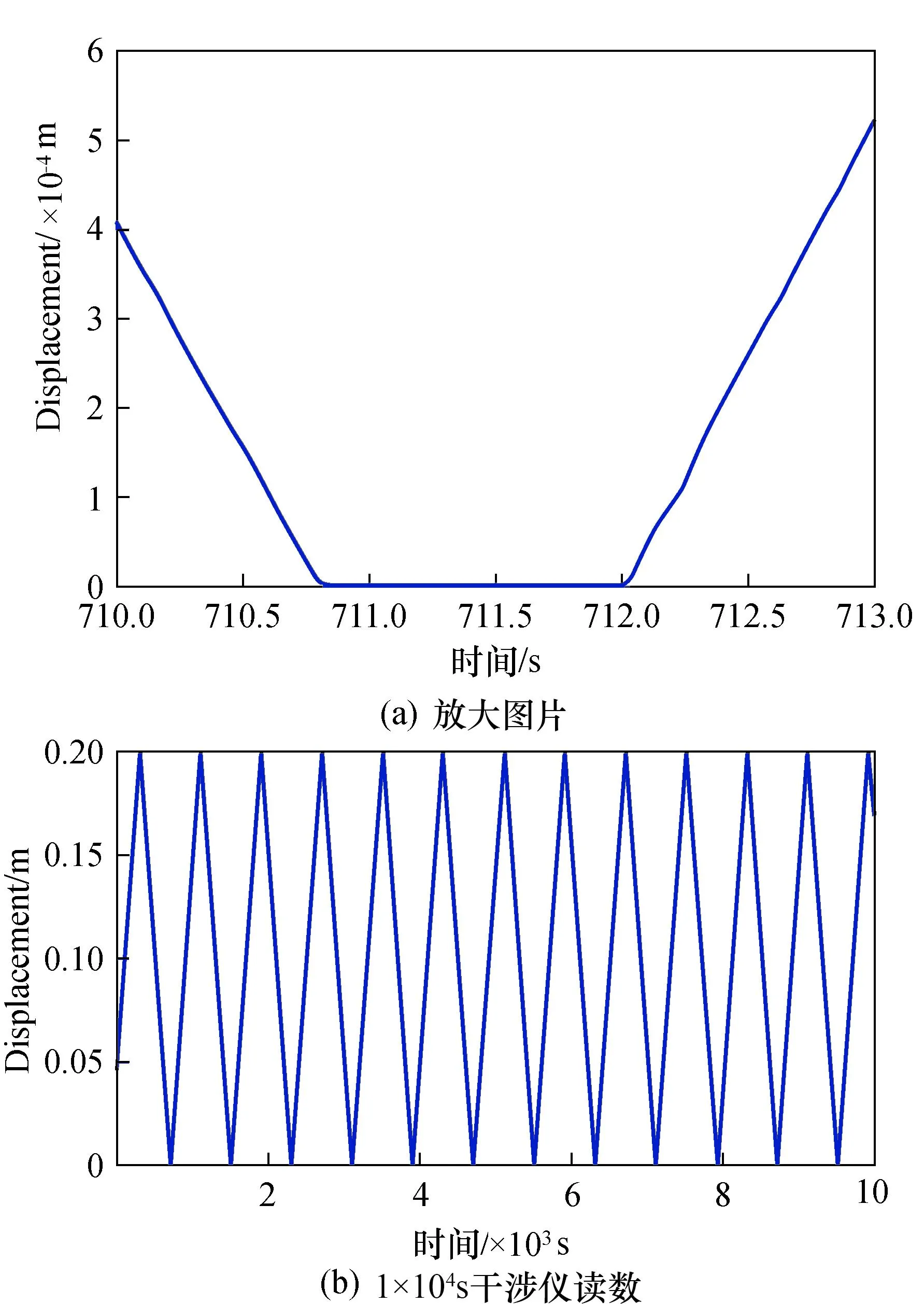
图7 长位移下的干涉仪表现Fig.7 Interferometer performance under long displacement condition

在约1×104s的时间内,锁相环工作状态良好,未出现失锁现象,见图7(b)。但将图片放大后可以看到,干涉仪的读数并非是一条理想的直线,见图7(a),这既有可能是长距离下位移台的“爬行”现象,也可能是干涉仪本身存在的误差。经测量,在100 mm的行程上,干涉仪读数的相对误差约为0.5‰,考虑到干涉仪是在大气环境中工作的,空气折射率和装配调整过程中的误差都可能造成误差,可以认为干涉仪工作不存在粗大误差。

3.4 短位移测试

换用精密纳米位移台,在较短位移下测试应答式干涉仪的工作状态。驱动位移台使之做阶梯运动,其结果如图8所示所示。位移过程持续了约325 s,精密位移台的步距为1 μm,位移台总共移动了25 μm,等效为几何路程变化50 μm。受振动影响,相位存在轻微波动。

图8 短位移下的干涉仪表现Fig.8 Interferometer performance under short displacement condition

在移动中,相位表读数改变了约46.895个周期,绝对误差约-80.74 nm,相对误差约为-1.6‰,精密位移台的分辨率为2 nm,两者相对比,明显测量存在系统误差。分析其原因如下:

1) 长距离位移台的可移动距离远长于短距离位移台,在光路装调过程中,反复令长距离位移台做满量程运动,最终能够使得光传播方向基本平行于位移台运动方向,最大限度减少了光路装调带来的误差;

2) 短距离位移台满量程运动距离仅100 μm,肉眼几乎不能分辨,粗调带来较大的光路不平行;

3) 实验中先完成了长距离位移台的测试,而后更换了短距离位移台,长距离位移台底板较低,对振动的抗性强,而短距离位移台底板较高,还需要加上转接板,因此振动影响较大。

尽管具有较大的系统误差,然而在短距离状态下,干涉仪的读数具有明显的阶梯型,显然能够正常运行。这也间接验证了应答式干涉仪的有效性。

4 结 论

开发了一套用于低频引力波探测的星间激光干涉测量模拟系统。通过光学锁相环将从激光器的相位锁定到功率仅在100 pW量级的稳定的主激光器的相位上,通过读取主激光器位置处外差信号的相位信息判断主、从卫星的相对位移。零漂测试显示环境温度、气压等带来的折射率变化和振动是噪声的主要来源,主激光器的频率噪声对装置表现影响较小。短位移测试和长位移测试均证明装置不存在粗大误差,但仍具有较显著的系统误差,这可能来自于光路装调的不理想。后续工作将主要聚焦于环境的优化,例如将装置置于温控良好的真空腔中,并辅以主动隔振系统。实验结果证明该模拟系统能够应用于后续星间激光干涉噪声模型标定任务。