AFM-TM微悬臂梁系统混沌运动及控制算法分析

宋佩颉, 褚衍东, 张 航, 俞 睿

(1.兰州交通大学 机电工程学院， 甘肃 兰州 730070；2.甘肃省计量研究院 长度计量研究所， 甘肃 兰州 730050)

1 引 言

近年来,量子力对纳米机电系统(micro-electromechanical systems,MEMS)的影响机理受到了相关学者广泛关注[1]。

原子力显微镜(atomic force microscope, AFM)作为一种典型的MESM,其主要工作原理是通过微悬臂梁系统和压变检测系统将原子间的范德华力转化为可由光电探测系统检测到的位移信号,通过位移信号的变化进而确定被测样品表面纳米级的形态特征[2～4]。AFM已经广泛应用于聚合材料、陶瓷、生物细胞等微纳米物质表面形态的测量和研究[5～7]。

轻敲模式原子力显微镜(atomic force microscope in tapping mode,AFM-TM)以其测量精度高,对被测样品表面形态破坏小等优点,已得到广泛应用。Chen Z Y等[8]研究发现,由于被测样品表面与AFM-TM微悬臂梁尖端之间原子力的影响,AFM-TM的微悬臂梁在特定参数条件会表现出包含有混沌运动的复杂动力学特性。微悬臂梁混沌运动的存在不仅会严重影响到AFM-TM的测量精度,大幅降低AFM-TM的分辨率,甚至会增加微悬臂梁探针尖端磨损,被测样品表面形态被破坏的风险[9, 10],在实际应用场景下,如何避免或消除混沌运动对测量精度的影响,是AFM-TM微悬臂梁系统混沌运动研究的重点。

为了提高AFM的测量精度和分辨率,可以通过动力学分析和参数匹配,构建一个相对稳定的微悬臂梁机械结构来降低复杂动力学特性对测量精度的影响,Zhang W M等[11]对AFM-TM微悬臂梁的机械结构进行了研究,并将其力学模型等效为一个质量-弹簧-阻尼系统,进行了振动特性分析,但并未讨论外部激励变化对系统振动特性的影响。

针对复杂的测量环境和变化的被测样品,仅通过动力学分析和参数匹配构建相对稳定的微悬臂梁机械结构是相对比较困难的,得益于现代控制理论的发展,将现代控制理论引入到机械结构复杂动力学控制中来,可以降低机械结构的加工难度,提高复杂多变环境下AFM-TM的测量精度和分辨率。

延时反馈控制是将系统的某一输出量与其延时的差值作为控制信号,再通过反馈增益对原系统进行控制[12, 13],该技术已经应用于诸多非线性机械系统中。文献[14]中提出了一种将延时反馈控制与模糊控制器相结合,用于抑制超声波电机混沌振荡的控制方法,取得了良好的结果。

本文首先根据AFM-TM微悬臂梁动力学方程建立系统的数学模型,研究当外部激励的参数发生变化时,微悬臂梁系统的非线性动力学特性,讨论微悬臂梁系统复杂动力学特性对AFM-TM测量结果的影响。在微悬臂梁系统动力学特性分析的基础上,对系统施加“延时反馈控制”和“模糊自适应延时反馈控制”,讨论不同控制算法下,系统动力学特性的变化,并对两种控制方法进行比较。结果对AFM-TM微悬臂梁外部激励参数选择、非线性系统复杂动力学特性分析和混沌运动控制提供了有意义的理论参考。

2 AFM-TM微悬臂梁建模

周期信号控制下AFM-TM微悬臂梁的原理如图1所示。

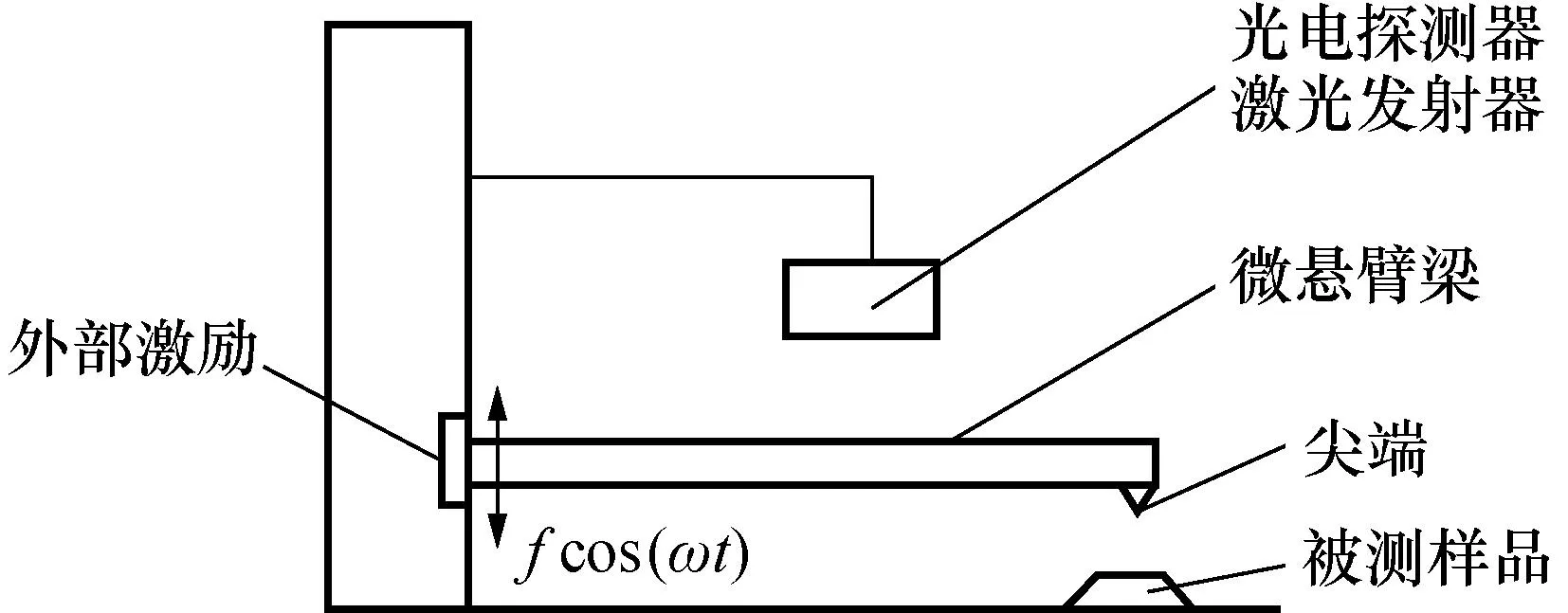
图1 原子力显微镜原理图Fig.1 Atomic Force Microscope Schematic

AFM-TM微悬臂梁的振动模型可以看作是一个质量-弹簧-阻尼系统,如图2所示。

图2 微悬臂梁的动力学模型Fig.2 Dynamic modeling of microcantilever beam

此时,假设微悬臂梁顶端的探针在加工时与微悬臂梁为一整体。由此可得,周期信号控制下微悬臂梁的运动方程为

(1)

如图2所示,微悬臂梁顶端的探针放大后,顶端是半径为R的球形,当微悬臂梁处于静止状态时,微悬臂梁与样品之间的距离为l0,微悬臂梁径向位移用x表示。系数k,c分别表示等效弹性系数和空气中的阻尼系数。

Fk表示为

Fk=-kx

(2)

由于微悬臂梁工作时的速度较小,Fc≪mg,所以Fc表示为

(3)

(4)

式中:Q表示微悬臂梁的等效质量因子;ω1表示微悬臂梁的固有振动频率。

F可以建模为球体和平面的相互作用,根据Lennard-Jones型式函数和文献[15～17]的研究,有

(5)

式中:A和B分别是排斥势和吸引势的Hamaker常数。因此,F可表示为

(6)

微悬臂梁系统由压电驱动器产生周期信号驱动,通过Fs进行谐波震荡

Fs=fcos (ωt)

(7)

联立式(1)～式(7),则微悬臂梁的运动方程为

+fcos (ωt)

(8)

令

(9)

式中:定义无量纲平衡距离为ls;定义无量纲时间参数为τ;x1、x2表示无量纲状态变量;kn表示原子间耦合弹性系数[18]。

对方程进行无量纲化处理,得到:

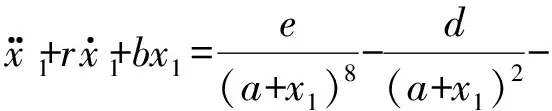
(10)

无量纲方程通过定义,可以转化为状态空间方程:

(11)

表1为AFM-TM微悬臂梁系统物理参数值。

其中,矩形微悬臂梁在自由端处的等效质量m的计算公式为

(12)

微悬臂梁顶端等效弹性系数k的计算公式为

(13)

将表1中的参数代入式(9),式(12),式(13),得到系统无量纲方程中对应参数值r=0.1,b=0.05,e=0.0001,d=4/27,a=1.6。当微悬臂梁在一阶共振频率下工作时,根据式(9),外部激励的频率比Ω=1。

3 AFM-TM微悬臂梁系统运动特性分析

本节尝试采用四阶Runge-Kutta法,利用Lyapunov指数、分岔图、Poincaré截面和相位图分析当外部激励幅值g变化时系统的运动特性,讨论微悬臂梁系统复杂动力学特性对AFM-TM测量结果的影响。数值仿真选取的初值条件均为x1=-0.4,x2=0.1。

3.1 数值仿真参数匹配

令r=0.1,b=0.05,e=0.0001,d=4/27,Ω=1,g=0.2,该组参数条件下,AFM-TM处于正常工作状态,微悬臂梁系统的位移-速度相位图如图3所示。

图3 g=0.2时,微悬臂梁系统x1-x2相位图Fig.3 x1-x2 phase diagram of micro-cantilever beam system at g=0.2

以幅值g为变量,取值范围[0,1.0],迭代步长0.000 2,得到对应AFM-TM微悬臂梁系统的分岔图、Poincaré截面和Lyapunov指数图如图4～图6所示。

图4 参数g变化时系统的分岔图Fig.4 Bifurcation diagram of the system as the parameter g is varied

图5 参数g变化时系统的Poincaré截面图Fig.5 Poincaré cross section of the system for variation of parameter g

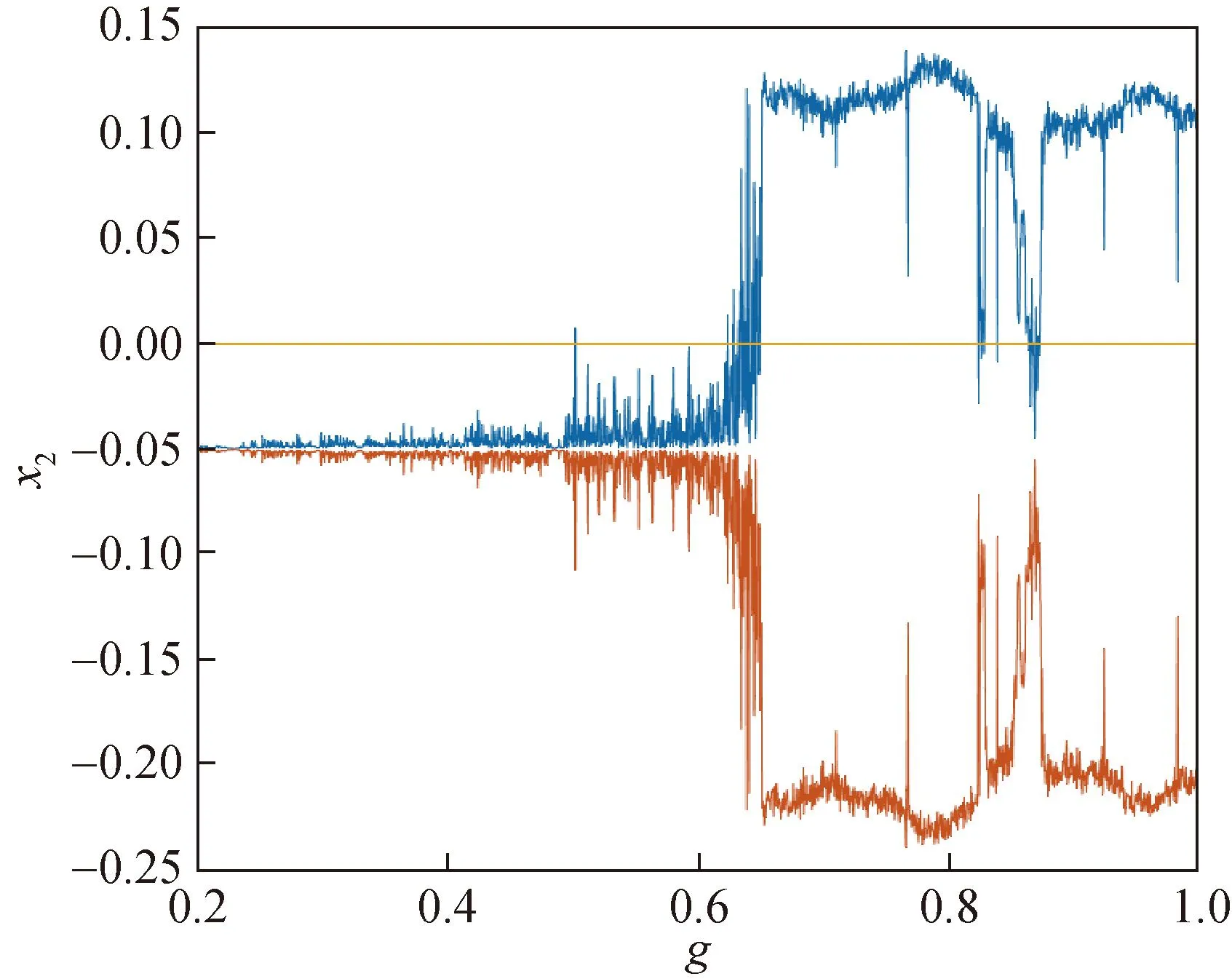
图6 参数g变化时系统的Lyapunov指数图Fig.6 Lyapunov exponential plot of the system for variation of parameter g

此时,系统的Poincaré截面上已经呈现出成片的密集点,且密集点具有层次结构,通过定性分析得出,当g∈[0,1.0]时,系统存在混沌运动状态。

由图6定量分析可得,当g∈[0.502 0,0.503 4]∪[0.627 6,0.628 4]∪[0.632 4,0.634 4]∪[0.646 4,0.647 6]∪[0.649 6,0.866 4]∪[0.822 8,1.000 0]时,系统处于混沌运动状态。

当g=0.8时,系统的位移-速度相位图如图7所示。

图7 g=0.8时,微悬臂梁系统x1-x2相位图Fig.7 x1-x2 phase diagram of micro-cantilever beam system at g=0.8

3.2 数值仿真结果分析

分析图3可知,当g=0.2,AFM-TM处于正常工作状态时,微悬臂梁系统的运动特性为稳定周期运动,此时AFM-TM的稳定性高,测得的图像分辨率高,能够获取被测样品准确可靠的表面形态特征。

当g=0.8时,如图4、图6、图7所示,AFM-TM微悬臂梁系统处于混沌运动状态,由Lyapunov指数的特性可知,当Lyapunov指数存在大于0的特征值λi(i=1,2,3)时,表现为相邻点信息量的丢失,特征值越大,信息量丢失越严重。同时,混沌运动特性表现出不稳定性和内随机性,这将导致AFM-TM无法准确测得被测样品表面的形态特征,表现为测量画面失真,无可读性。

进一步分析图7可知,当微悬臂梁系统处于混沌运动状态时,微悬臂梁的瞬时位移值显著增大,实际使用过程中,表现为增加了样品表面形态和微悬臂梁尖端部分损伤的风险。

值得注意的是,当g在特定参数区间取值时,微悬臂梁系统的运动特性表现为介于周期运动和混沌运动的类周期运动,以g=0.87为例,此时,系统对应的Lyapunov指数特征值小于0,位移-速度相位图如图8所示。

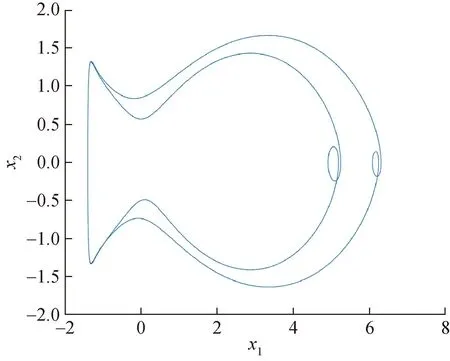
图8 g=0.87时,微悬臂梁系统x1-x2相位图Fig.8 x1-x2 phase diagram of the microcantilever system when g=0.87

此时系统的运动特性表现为4倍周期运动,虽然系统对应的Lyapunov指数特征值小于0,但AFM-TM采集到图像表现为存在虚影,对于微纳米测量仪器而言,虚影的存在增加了高精度测量的难度。所以,仅考虑对测量精度的影响,诸如4倍周期的类周期运动与混沌运动一样,对于AFM-TM微悬臂梁系统而言,均是需要避免或消除的。

4 微悬臂梁系统延时反馈控制

在AFM-TM实际使用过程中,由于受外部因素干扰和客观条件的限制,使得AFM-TM微悬臂梁系统在特定条件下,不可避免的工作于类周期参数区间甚至混沌参数区间。尝试将延时反馈控制与AFM-TM微悬臂梁系统相结合,以达到增大微悬臂梁系统参数选择区间,提高AFM-TM测量精度和分辨率的目的。

延时反馈控制的控制框图如图9所示,其数学表述式可表示为

图9 延时反馈控制框图Fig.9 Block diagram of delayed feedback control

Fd(τ)=K[x2(τ-υ)-x2(τ)]

(14)

式中:Fd(τ)表示延时反馈控制力;υ表示无量纲时间延迟量;x2(τ-υ)表示微悬臂梁系统无量纲延迟速度;K为延时反馈增益系数。

将式(14)所代表的延时反馈控制加载在公式(11)的第二项中,得到:

(15)

延时反馈控制的优点在于,其控制的变量中包含有其他变量的不稳定分量,由此便不需要在每个变量上都加入控制量。所以在微悬臂梁系统中,只需要控制一个变量x2(τ)。

在施加延时反馈控制之前,需要首先确定公式(15)中参数υ和K的取值。

υ被选定为2个相邻的输出信号极大值之间的时间间隔,当系统出现混沌运动,通常选择系统参考状态的稳定周期值作为υ的取值。以图3参数条件运动状态为系统的参考状态,此时υ的取值为6.28。

K的取值范围可以通过分岔图进行定性分析,进而通过Lyapunov指数特征值进行定量确定,以K为变量,将延时反馈控制引入图7对应参数条件下的系统,引入延时反馈控制后系统分岔图如图10所示。

图10 系统混沌运动时引入延时反馈控制后的分岔图Fig.10 Bifurcation diagram after introducing delayed feedback control during chaotic motion of the system

对图10分析可得,当K的取值在[0.212,0.260]区间内时,结合相位图可知,延时反馈控制可以将系统的混沌运动拉回到稳定周期轨道;当K<0.212,延时反馈控制因控制系数K的取值过小,表现为控制不足;当K>0.26时,由于控制系数K的取值过大,系统超调,微悬臂梁系统与延时反馈控制系统组成了一个新的不稳定系统。

当K=0.25时,图7参数条件下引入延时反馈控制后的位移-速度相位图如图11所示。

图11 微悬臂梁系统混沌运动引入延时反馈控制后的x1-x2相位图Fig.11 x1-x2 phase diagram of the chaotic motion of the microcantilever system after the introduction of delay feedback control

由此可以得出结论,当υ=6.28,K=0.25时,延时反馈控制可以有效的将图7参数条件下微悬臂梁系统的混沌运动拉回到周期轨道。

5 微悬臂梁系统模糊自适应延时反馈控制

延时反馈控制中K确定后,其大小不能变化,如果系统参数发生变化或改变被测样品时,就有可能导致反馈控制失效。

为了克服延时反馈控制区域小的缺陷,本节尝试将模糊延时反馈控制应用于AFM-TM微悬臂梁的混沌运动控制当中。

其控制框图如图12所示。

图12 模糊自适应延时反馈控制框图Fig.12 Fuzzy adaptive time-delay feedback control block diagram

模糊控制器的两个输入分别是被控微悬臂梁系统的运动速度和其延时的差值,即误差信号e,以及由e生成的误差变化率ec,表示为:

e=e(τ)=x2(τ-υ)-x2(τ)

(16)

(17)

由图12可得,模糊控制器模块代替了延时反馈控制中的控制增益K。其中,Ke表示误差控制增益,随着Ke的增大,系统调节时间变长,稳态误差变小,当Ke的取值过大时,会使系统发生超调,且过渡过程过长;Kec表示误差变化率控制增益,随着Kec的增大,系统超调量减小,但系统的响应速度变慢,而且,Kec对超调的遏制作用十分明显。Kx表示控制比例因子,Kx增大会使系统精度提高,响应加快,但Kx过大会使系统产生较大超调,甚至发散,而Kx过小会使系统过度时间变长。

综上所述,当误差e和误差变化率ec较大时,采用较小的Ke,Kec和较大的Kx来加快系统的响应速度;当误差e和误差变化率ec较小时,采用较大的Ke,Kec和较小的Kx来降低系统的稳态误差,抑制超调。

设e、ec以及输出变量论域均为[-6,6],其模糊子集为{NB,NM,NS,ZO,PS,PM,PB},即{负大,负中,负小,零,正小,正中,正大}。e和模糊控制器输出u的隶属函数为高斯型函数,ec的隶属函数为三角型函数,解模糊采用重心法,设计的模糊规则如表2所示。

表2 模糊控制规则Tab.2 fuzzy control rules

模糊控制规则以“if-then”形式表示,如:

R1: ifeis NB andecis NB thenuis NB;

R2: ifeis NM andecis NB thenuis NB;

R3: ifeis NB andecis NM thenuis NB;

⋮ ⋮

Rn: ifeis PB andecis PB thenuis PB。

在图7所示微悬臂梁系统混沌运动参数条件下,引入模糊自适应延时反馈控制,分别选取Ke=0.6,Kec=0.4和Kx=4。系统引入模糊自适应延时反馈后的相位图如图13所示。

图13 微悬臂梁系统混沌运动引入模糊自适应延时反馈控制后的位移-速度相位图Fig.13 The displacement-velocity phase diagram of the chaotic motion of the microcantilever system after the introduction of the fuzzy adaptive delay feedback control

由图13可知,模糊自适应延时反馈控制同样可以将处于混沌运动状态下的微悬臂梁系统带回到周期轨道上。

结合第3节延时反馈控制,从实现难度和有效控制范围两方面,对两种控制算法进行比较。

延时反馈控制的优点在于算法简单,缺点在于反馈增益系数K的求取难度相对较大,且反馈增益系数K无法自动调节,导致延时反馈控制的有效控制范围较小。相较而言,模糊自适应延时反馈控制虽然算法相对复杂,但可以通过模糊控制规则,在系统不同参数条件下自动调节模糊控制器输出,通过对Ke、Kec和Kx进行调节,不但可以尽量降低稳态误差,还能保证系统不会超调。

综上所述,模糊自适应延时反馈更适用于AFM-TM被测样品多样,微悬臂梁数学模型等效参数变化的复杂条件下的精密测量。

6 结 论

本文对AFM-TM微悬臂梁非线性运动特性进行研究的结果表明,当外部激励幅值参数取值在特定范围内时,系统表现出混沌运动特性。在AFM-TM微悬臂梁系统中,混沌运动的不稳定性和内随机性,将导致AFM-TM无法准确测得被测样品表面的形态特征,表现为测量画面失真,测量数据无可读性。因此,通过引入外部控制器,将系统从混沌运动拉回到预定的周期轨道中显得尤为重要。为此,提出了两种控制方案:延时反馈控制和模糊自适应延时反馈控制,并对这两种控制方案进行了比较。

仿真结果表明:AFM-TM微悬臂梁系统的混沌运动是可控的,延时反馈控制和模糊自适应延时反馈控制均能实现对系统混沌运动的控制,并将系统稳定在预定的轨道上,但模糊自适应延时反馈控制避免了对反馈增益系数的求取,同时可根据控制参数的变化,自主调节量化因子和比例因子的取值,更适用于AFM-被测样品变化的复杂情况。其结果不仅能为非线性动力学混沌运动特性分析和控制提供有意义的理论参考,同时为微悬臂梁系统混沌运动控制选择提供了依据,并对AFM-TM的测量精度的提高提供了重要的理论基础。