融合颜色与形状信息的铁谱磨粒链分割方法研究

杨海，盛晨兴

(1.武汉理工大学船海与能源动力学院，湖北武汉 430063；2，水路交通控制全国重点实验室(武汉理工大学)，湖北武汉 430063；3.国家水运安全工程技术研究中心，湖北武汉 430063)

由机械设备磨损而产生的磨粒通常包含关于摩擦部件磨损状况的有效信息，磨粒分析被广泛用于机械设备磨损检测[1]。铁谱磨粒分析技术通过对磨粒的特征(面积、周长、纹理特征、颜色信息等)进行提取与分析，可以对机械设备的润滑以及磨损状态进行评估，并对故障检测及检修提供依据[2]。

在铁谱图像中，单磨粒记录的是局部瞬间的磨损情况，而磨粒群体的共性特征代表着当前设备的主要磨损状态，提取具有足够样本数量磨粒的统计特征是提高铁谱分析准确性的关键[3]。目前，对于单磨粒的特征提取与分析技术已经较为成熟[4-6]，在实际应用中，铁磁性磨粒因磁场作用在铁谱图像中堆叠成链，能否对铁谱图像中的磨粒链进行有效分割直接影响后续磨粒参数提取的精度[7]。WU等[8]指出对磨粒链的处理比对单个磨粒的处理更为重要。

针对磨粒链的分割问题，李峰等人[9]首次运用数学形态学的方法，通过对二值化后的磨粒图像实施形态学开运算，并结合拉普拉斯算子，有效地提取出单个磨粒形状。WU等[10]基于“极限腐蚀-条件膨胀”提出一种多尺度分割方法，采用不同的腐蚀尺度，结合一定的终止准则，实现了在线铁谱的磨粒链分割。WANG等[11]提出一种融合标记分水岭与蚁群聚类的方法，通过对过分割区域进行合并，从磨粒链中提取了异常大磨粒。然而不同磨粒之间尺寸、纹理、颜色各不相同，针对磨粒链的分割结果均存在一定过分割或欠分割现象。

本文作者针对磨粒链图像特点，利用改进形态学运算对磨粒链图像进行预分割，消除干扰因素影响，然后利用标记分水岭与自适应阈值灰色聚类对磨粒链进行分割。

1 基于形状信息的磨粒链预分割方法

磨粒链是由若干单磨粒堆叠而成[12]，其中也可能包含异常大磨粒，这些链状磨粒分布无规律，且经常会出现链与链之间互相黏连的情况，如图1所示，而这些都会影响磨粒链分割的精度。因此，文中基于形状信息，利用改进形态学方法对磨粒链图像进行预分割。

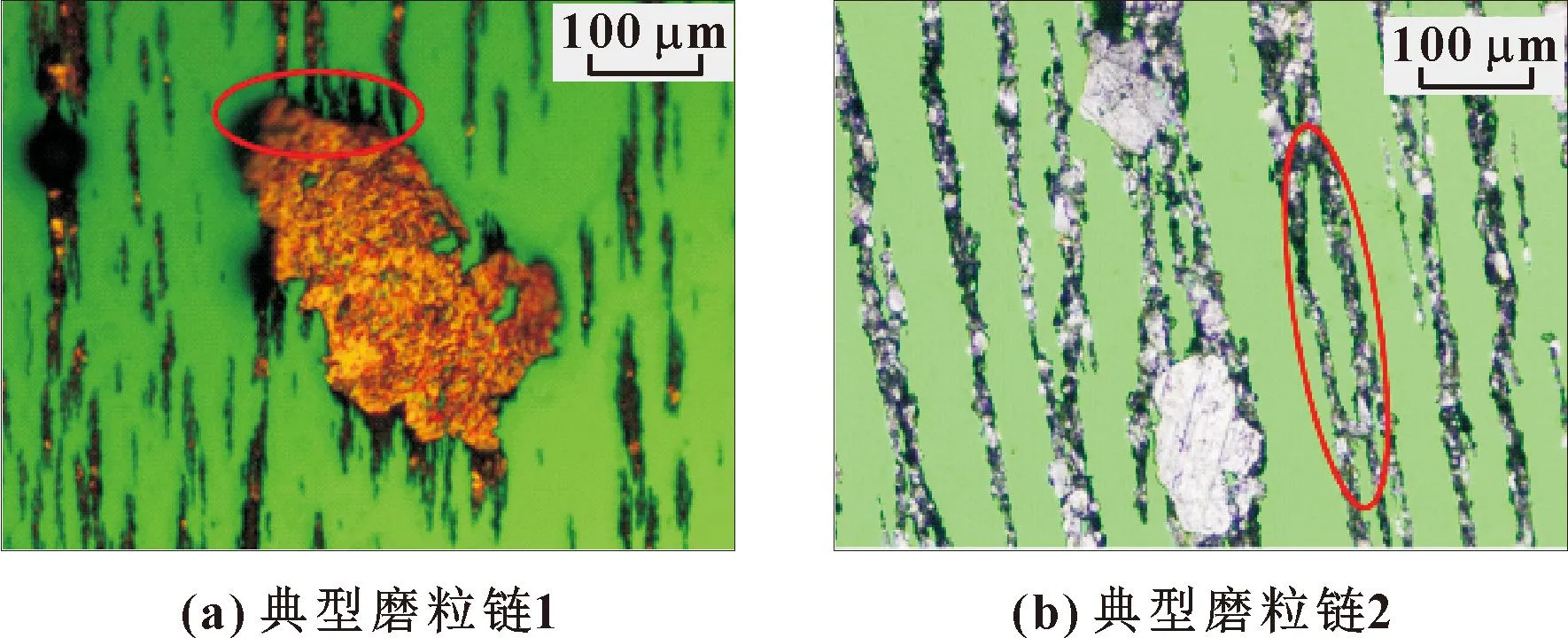
图1 典型磨粒链图像

1.1 磨粒链黏连部分分割

数学形态学中2种基本运算为腐蚀、膨胀。膨胀是指图像中为其边界添加像素点，而腐蚀是其逆过程[12]。极限腐蚀是将目标区域腐蚀到与结构元素矩阵相似的核尺度上，条件膨胀(Conditional Expansion)是指在原有目标图像区域内进行膨胀运算，且膨胀后各区域之间没有重叠[9]。针对磨粒链之间互相黏连的情况，基于“极限腐蚀-条件膨胀”对图像进行均匀腐蚀，腐蚀后的图像中各区域分别为M1、M2、…、Mn，将符合式(1)条件的区域视为不存在磨粒链互相黏连的情况，并对其进行条件膨胀与初始区域分割开。对可能存在黏连现象的区域重复上述操作，为防止过分割，腐蚀次数上限设置为3次。

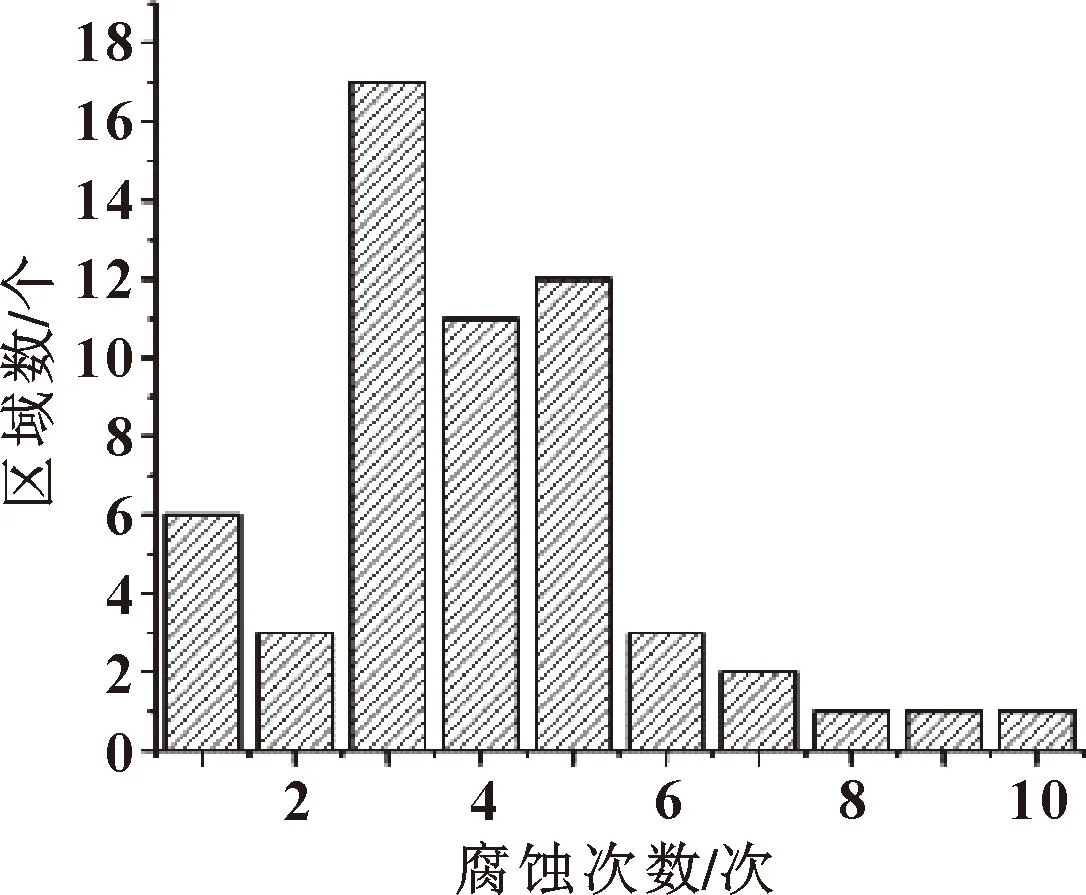
Mii

(1)

式中：Mii为连通域短轴长；MTi为黏连阈值，MTi=w/40，w为图像横向像素值大小。

以图2(a)所示磨粒链图像为例，将其转换为二值图形式，如图2(b)所示；然后进行均匀腐蚀，将符合条件的区域进行条件膨胀，与原始区域分割开；对剩余区域重复上述操作，得到最终分割结果如图2(c)所示，可以看到图中所标记的几处黏连区域均已断开。

图2 磨粒链黏连部分分割

1.2 异常大磨粒与磨粒链分割

形态学中的闭运算具有消除物体周围细突出物的特点，将异常大磨粒周围磨粒链视为“细突出物”，利用极限腐蚀得到异常大磨粒的“核”，对其进行条件膨胀即可使其与周围细长磨粒链分割开。

以图1(a)为例，腐蚀终止条件设为连通域数量增加后变为1且不再增加。连通域数量与腐蚀次数关系如图3所示。

图3 连通域数量与腐蚀次数的关系

经8次腐蚀操作后连通域变为1且不再增加，对腐蚀后图像进行条件膨胀得到分割结果如图4所示，可以看出图中的异常大磨粒已被成功提取。

图4 异常大磨粒提取结果

为验证该预分割方法的精度，选取5张磨粒链图像，事先对图中异常大磨粒以及磨粒链黏连部分进行标记，与预分割方法的分割结果进行对比，结果如表1所示。可知，标记的异常大磨粒均得到了有效提取，而磨粒链之间的黏连部分分割率也达到90%以上，表明该预分割方法精度较高。

表1 磨粒链图像预分割精度分析

2 基于颜色信息的磨粒链分割方法

2.1 标记符分水岭与灰色聚类

基于标记符的分水岭算法基本思想是在原图中提取前景与背景标记来引导并限制分水岭的分割区域。在离线铁谱图像中，前景磨粒所呈现的形态复杂多变，但背景灰度值却相对一致，因此，阈值法常常被用于铁谱图像的分割[14]。

以图5所示磨粒链图像为例，首先采用扩展最大变换(H-max变换[15])：

(2)

图5 磨粒链图像

式中：Pmark(x，y)为前景标记图像；Irec(x，y)为复合开闭重建后的图像。

利用距离变换得到分水岭脊线图，将其作为背景标记图像，对叠加标记符的灰度梯度图像进行分水岭变换，结果如图6所示。

图6 标记分水岭分割

由图6可知，标记符的引入一定程度上缓解了分水岭过分割问题，但在某些沉积链区域仍存在过分割问题，在大磨粒区域更为严重。原因是磨粒链图像的纹理信息较为复杂，在提取前景标记时，容易提取到多余的局部最小值。因此，利用灰色聚类将相似区域归并。

灰色关联度(Gray Relational Degree)作为灰色理论体系的一部分，具有计算简单、低冗余等特点[12]。设集合xi={xi(1)，…，xi(n)}，(i=1，2，…，m)，则任意两集合i、j间关联系数计算公式为

(3)

式中：Δij=|xi(k)-xj(k)|；Δmax=max{Δij}；Δmin=min{Δij}；ξ∈(0，1]为观测系数，文中取值0.5。

则任意两集合i、j间的关联度为

(4)

针对铁谱磨粒链图像的特点，设图中某区域Mi中的像素点集合为(Xm，Ym)，提取该区域RGB与Lab各通道分量的平均值作为其颜色特征参数。由于不同铁谱图像上磨粒颜色差异较大，其颜色信息的平均数、方差等存在差异，因此引入颜色系数对关联度计算公式进行优化：首先计算整张图像中磨粒链区域RGB与Lab各颜色通道标准差S，然后将其归一化，得到权重系数矩阵W：

(5)

将权重系数矩阵W加入到关联度计算公式中，计算各联通区域之间的关联度，得到关联度矩阵R：

(6)

对图像中连通区域进行归并的前提是两区域相邻，因此在计算关联度矩阵时引入位置关系矩阵L：

(7)

(8)

2.2 自适应阈值灰色聚类

由于不同磨粒链尺寸不一，在拍摄过程中受镜头景深影响，可能会使图像周围以及尺寸较小的磨粒链所能提取到的颜色较模糊，从而导致这些区域经标记分水岭分割后的关联度整体高于其他区域，若要将其中单磨粒分割出来，则需要较高的归并阈值。传统灰色聚类将归并阈值设为常数，显然不能满足该需求。

因此，提出一种自适应阈值(Adaptive Threshold)的灰色聚类(ATG)方法，引入描述参数，以聚类结果中单磨粒形状特征作为描述聚类结果好坏的参数，设置初始阈值并均匀增加，计算每次聚类后描述参数的值，将描述参数最大时对应的阈值作为最佳阈值。描述参数计算公式如下：

(9)

(10)

对比不同阈值下描述参数的大小，确定最佳归并阈值。以图7(a)所示磨粒链为例，其标记分水岭分割结果如图7(b)所示，分别以0.9～0.99作为归并阈值进行灰色聚类，得到聚类结果如图7(c)—(l)所示，每次聚类的归并阈值P与描述参数η的关系如表2所示。可见，当P=0.96时描述参数值最大，此时灰色聚类效果最佳，如图7(i)所示。

表2 归并阈值与描述参数的关系

图7 不同归并阈值条件下的聚类结果

3 融合颜色与形状信息的磨粒链分割

融合颜色与形状信息的磨粒链分割方法流程如图8所示。

图8 磨粒链分割方法流程

具体步骤如下：

(1)基于图像形状信息，利用改进形态学运算对其进行预分割处理，提取出异常大磨粒并断开磨粒链黏连部分。

(2)基于图像的颜色信息，利用标记符分水岭对预分割处理后的磨粒链图像进行分割。

为验证该方法的有效性，以图5所示磨粒链图像为例进行分割，图9所示为其预分割处理后的结果。

图9 预分割结果

图10(a)与图10(b)所示分别为结合传统灰色聚类、结合自适应阈值灰色聚类的标记分水岭分割结果。

图10 不同分割方法分割结果

从图9和图10可以看出，相较于以往分割方法，文中所用方法对磨粒链图像进行了预处理，消除了异常大磨粒及磨粒链黏连区域对磨粒链分割的影响；其次，利用自适应阈值灰色聚类对标记分水岭分割结果中的过分割区域进行归并，相较于传统灰色聚类具有更好的适应性，能有效防止单一阈值所产生的欠分割现象。结果表明，该方法具有一定的优越性。

为验证其可行性，以各区域RGB与Lab各颜色通道的标准差作为参数，利用Cd作为描述区域颜色差异度的指标，其计算公式如下：

(11)

式中：Chi为区域i中各颜色通道；σ(Chi)代表该颜色通道的标准差。

计算图5中各磨粒链区域的颜色差异度并与其最佳归并阈值进行比较，结果如表3所示。可知，最佳归并阈值与颜色差异度大小呈负相关趋势，即颜色差异程度越大，最佳归并阈值越小，结论与实际情况相符，证明该方法具有一定可行性。

表3 区域颜色差异度与最佳归并阈值关系

4 结论

针对铁谱磨粒链图像不同区域的特点，提出一种融合颜色与形状信息的磨粒链分割方法：首先基于形状信息，利用改进形态学方法对图像进行预分割处理，成功提取出异常大磨粒并断开磨粒链黏连部分；然后基于颜色信息，利用标记分水岭方法对磨粒链区域进行分割，在此基础上结合形状与颜色信息，利用自适应阈值灰色聚类对标记分水岭分割结果进行修正。结果表明，该方法精度较高，适用性较好。最后，引入颜色差异度指标，计算各磨粒链区域的颜色差异度，观察发现其大小与最佳阈值呈负相关趋势，结论与实际相符，证明该方法具有一定可行性。