径向不对中微织构气体箔片轴承静态特性分析
2024-04-17何振鹏邹雨辰王智赵福星于昊黎柏春刘泉辛佳
何振鹏,邹雨辰,王智,赵福星,于昊,黎柏春,刘泉,辛佳
(1.中国民航大学航空工程学院,天津 300300;2.重庆航天职业技术学院,重庆 400021;3.鄂尔多斯应用技术学院大飞机学院,内蒙古鄂尔多斯 017000)
近年来,人们越来越关注建立更精确的模型以及如何优化气体轴承结构以最大限度地提高其承载能力。研究表明,轴承的液膜压力和摩擦力矩等性能在很大程度上取决于表面纹理参数[1-3]。目前表面织构技术已经被证明是一种改善摩擦学特征的有效手段[4]。
表面微织构技术的原理是利用微坑或者微沟槽产生一定的流体动压等效果来降低摩擦,提高表面承载力。通过人工表面织构改善表面摩擦学特性的设计思想源于20世纪60年代,HAMILTON等[5]提出了利用表面微凸起来产生附加动压润滑效果的想法。BRIZMER等[6]建立了带有纹理的并联滑块模型,分析了表面纹理对承载能力的影响。此后,SHINDE和PAWAR[7]为了提高滑动轴承的性能,采用多目标优化方法确定最佳表面粗糙度参数,并研究了不同槽参数下的轴承性能。类似地,GANAI等[8]对自作用式空气箔片径向轴承的顶部箔片上的微织构、微槽和微腔进行了研究。研究表明,微型口袋顶部箔片轴承的摩擦因数降低幅度最大,降低了8%~11%。此外,国内王玉君等[9]对 4 种非金属材料的织构型推力轴承进行了优化,结果表明轴承最优织构参数间相互影响。ZHANG等[10]基于3种微织构分布类型,进一步分析了相对微织构深度和微织构排布的影响。结果表明,微织构的合理排列可以使气体箔片轴承承载力的最大增量超过10%。目前,表面微织构技术已经初步应用于油润滑摩擦副,但通过表面结构设计来改善气体轴承性能的研究还比较少,已有的气体轴承微织构数学模型也较为简单。此外,对于微织构的研究还没有形成具有指导意义的设计方法和理论。因此对于微织构参数的研究,可以为微织构轴承的表面优化设计提供参考。
不对中是旋转机械中最常见的故障之一,目前轴承的不对中问题已有广泛的研究。FENG和ZHAO[11]的研究表明,随着轴承间隙的减小和不对中角度的增大,轴承具有较大的刚度。此外,LI和XIE[12]综合考虑了稀疏效应和不对中作用下MEMS(微机电系统)气体轴承综合性能的变化规律。研究结果表明,不对中会降低轴承的稳定性。以上研究结果表明,轴承不对中问题不容忽视。
关于表面粗糙度方面的研究,WEI等[13]的实验结果表明,许多工程表面的粗糙度高度分布满足高斯分布,表面轮廓具有指数自相关函数关系;ZHANG等[14]使用光学数字显微镜观察轴承顶部箔片上支撑表面的横截面,测量出样品的表面粗糙度高度分布符合高斯分布。陈辉等人[15]基于随机过程和时间序列模型理论,利用Johnson转换系统模拟得到了高斯和非高斯粗糙表面;将模拟得到的粗糙表面的自相关函数值与理论值对比发现,在一定条件下两者误差较小,说明提出的模拟方法是可行的。因此,文中引入高斯随机粗糙度来模拟轴承在实际加工过程中产生的粗糙度。
考虑到径向气体箔片轴承的实际工况,本文作者考虑轴承的轴颈不对中和表面粗糙度,以径向不对中气体箔片轴承为研究对象,将多种形式的微织构引入到轴承中,利用MATLAB软件,通过超松弛迭代法(SOR)和有限差分法求解轴承的Reynolds控制方程,得到不同微织构参数下的轴承承载力、摩擦力矩等静特性。通过对轴承静特性的分析,确定了一组可以提高气体箔片轴承静特性的微织构参数。
1 理论及数值分析
1.1 理论模型
图1所示为径向不对中微织构气体箔片轴承的结构模型。假设轴和轴承具有相同的表面粗糙度σs,微织构位于平箔片上。微织构在平箔片展开面上分布如图2所示。
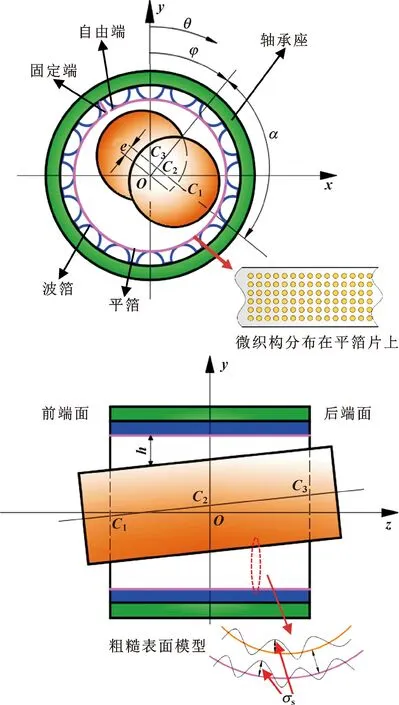
图1 微织构径向气体箔片轴承示意图(轴颈不对中)
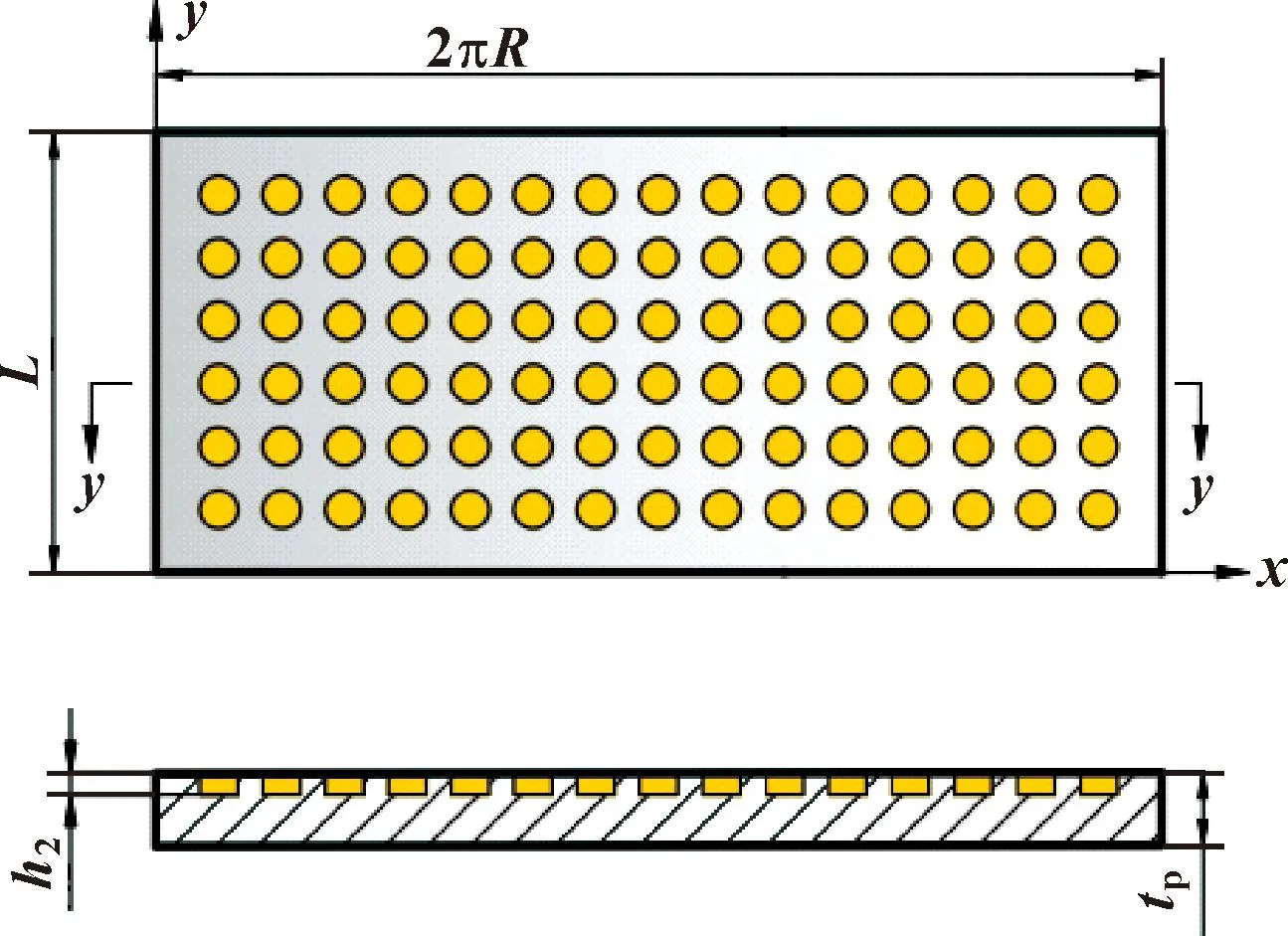
图2 平箔片展开面上微织构分布示意
对于在稳态下运行的气体箔片轴承,Reynolds方程[16]可写成如下等式:
(1)
忽略波箔变形引起的膜厚变化,考虑粗糙度与表面微织构的情况下不对中气体箔片轴承气膜厚度可以表示为
h=c+ecos(θ-φ)+tanγ(y-L/2)cos(θ-α-φ)+hs+h′
(2)
式中:c是半径间隙;e是轴承中心截面偏心距;θ是从y轴正方向起的角坐标;φ是轴承与轴颈中心的连线oc2与z轴的夹角;γ是轴颈在轴承中的倾斜角;l是轴承宽度;α是oc2与c1c3之间的夹角,其中c1、c2、c3是轴颈轴向与前端面、中间截面、后端面的交点;hs为轴颈和轴承表面叠加粗糙度,hs=2σs;h′为微织构气膜厚度。
1.2 粗糙表面的数学模型
高斯随机粗糙表面可以采用二维数字滤波技术得到。首先利用MATLAB生成一个高斯分布随机序列η(i,j),将所需的自相关函数进行傅里叶变换,得到功率谱密度函数Sz(ωx,ωy)。自相关函数多采用指数型函数,其表达式[17]为
Rz(k,l)=σ2exp{-2.3[(k/βx)2+(l/βy)2]1/2}
(3)
式中:σ为表面均方根粗糙度;βx和βy分别为x和y方向上的自相关长度。
将自相关函数进行傅里叶变换得到功率谱密度:
(4)
输入序列η(i,j)是独立的随机序列且服从高斯分布,该序列功率谱密度为常数C=1。输入滤波器的传递函数H(ωx,ωy)可表示为
H(ωx,ωy)=[Sz(ωx,ωy)/C]1/2
(5)
将传递函数进行傅里叶逆变换得到滤波器中的冲击响应函数h(k,l):
(6)
最后采用二维数字滤波技术就可模拟生成具有指定自相关函数的高斯随机粗糙表面,即随机表面z(i,j),其表达式为
(7)
1.3 微织构模型
文中网格划分规格为m×n=300×70,使各个网格的周向和轴向尺寸近似,所研究的7种微织构的具体形式及其约束方程和气膜厚度方程如表1所示。
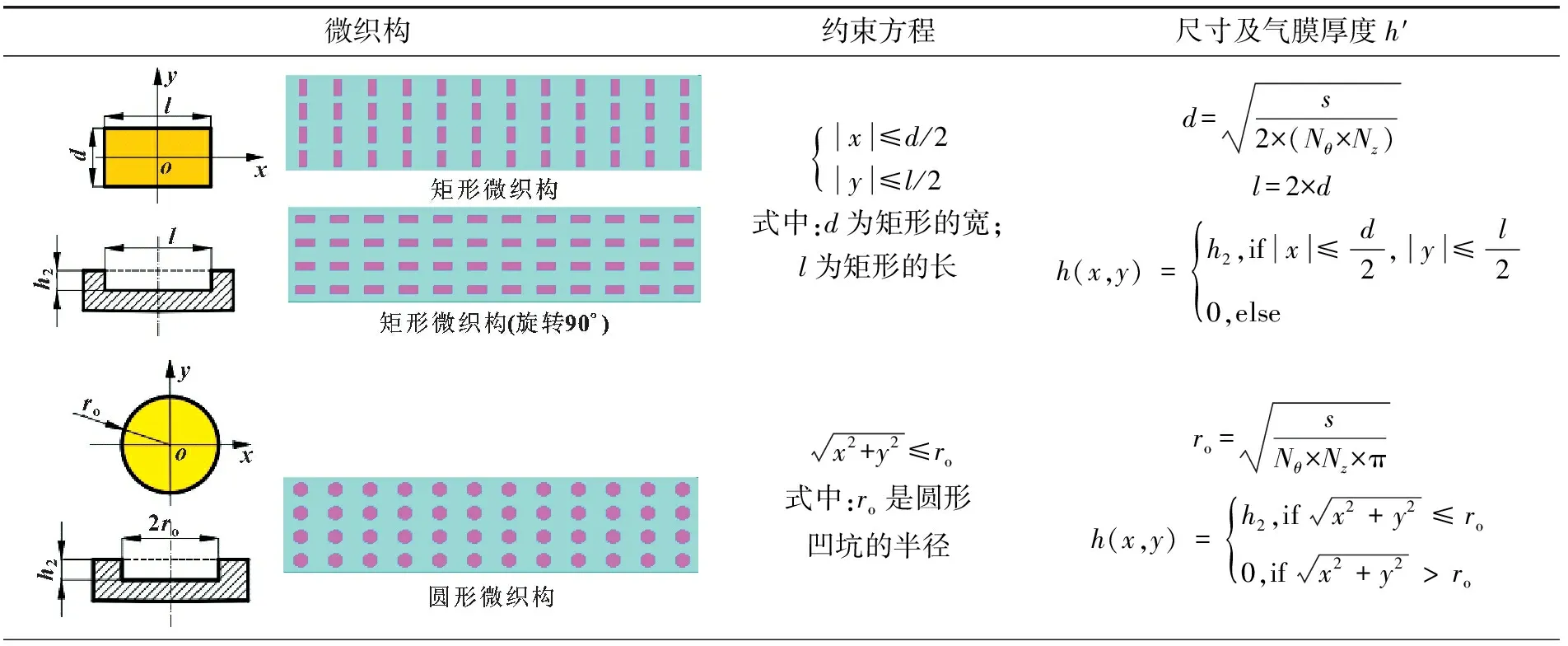
表1 微织构形状及其约束方程和气膜厚度方程
表中:a′是微织构总面积在轴承平箔片总面积中所占的比例;Nθ×Nz是微织构周向×轴向的数量;S是轴承平箔片展开的总面积S=2πRL;s是微织构总面积,s=S×a′。
2 数值计算
2.1 求解Reynolds方程
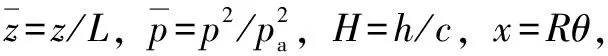
(8)
对量纲一化形式的Reynolds方程进行离散化并整理成如下形式:
(9)
其中,
从轴承的结构示意图中可知,平箔片的自由端与固定端并未连接,轴承端面与外界环境相接,因此轴承所满足的边界条件为
(10)
引入松弛因子ω来改善收敛条件,将第n次计算的结果与n-1次计算的结果加权平均作为最终第n次计算的结果,即:
(11)
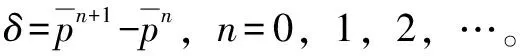
文中在求解过程中使用的收敛相对误差为
(12)
2.2 轴承静特性计算
文中研究的气体箔片轴承的静态特性包括承载力和摩擦力矩。
(13)
总的量纲一承载力:
(14)
有量纲的承载力为
(15)
轴承的量纲一摩擦力矩可表示为
(16)
径向气体箔片轴承的摩擦力矩为
(17)
2.3 计算对象及模型验证
文中所研究的径向气体箔片轴承的参数如表2所示。
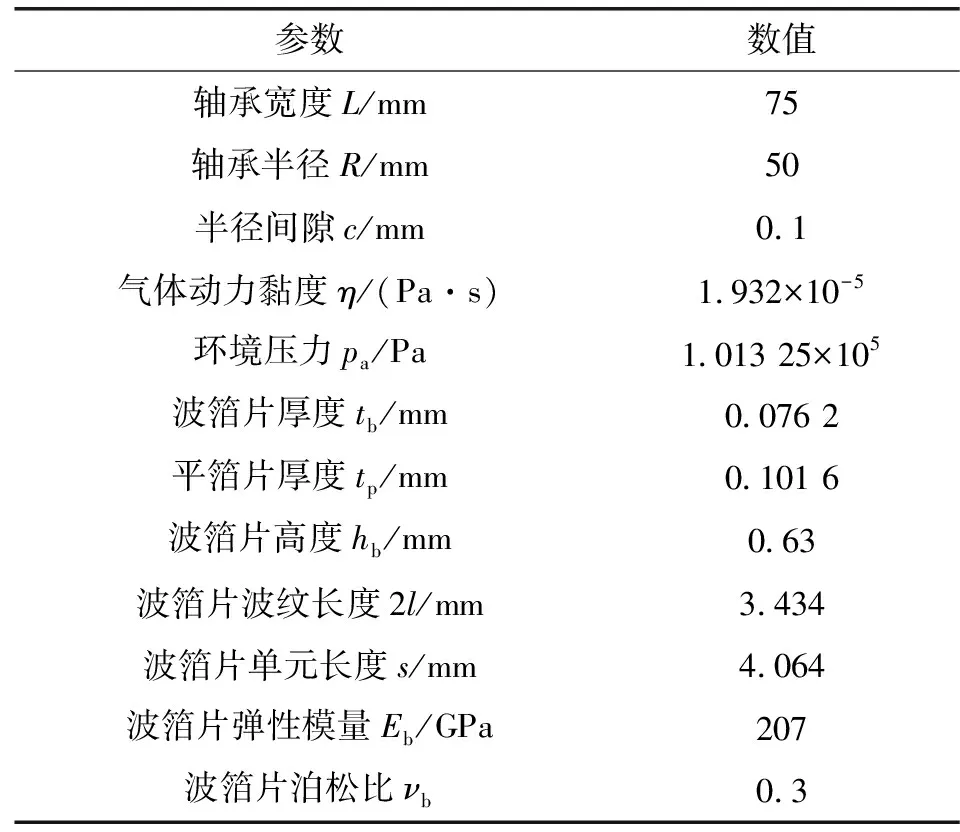
表2 轴承主要参数
图3所示为刚性表面空气轴承在空气最小气膜厚度为 16 μm、转速为30 000 r/min时得到的中截面量纲一压力和气膜厚度分布及与文献[17]中数据对比。可以看出计算数据与文献数据吻合度很高,压力值最大偏差不超过5%,气膜厚度分布完全吻合,说明计算方法可行。

图3 轴向中截面量纲一压力和气膜厚度分布
3 结果及分析
3.1 微织构形状对气体箔片轴承性能的影响
文中探究7种不同形式的微织构对轴承承载力和摩擦力矩的影响。运行参数如表3所示。

表3 运行参数
图4所示为不同微织构深度下,7种微织构气体箔片轴承的承载力变化曲线,微织构数量设置为Nθ×Nz=24×8。可以看出,当微织构深度达到35 μm时,轴承承载力相比于无微织构时得到了提升,其中椭圆形微织构的承载力提升最高,比无微织构轴承增大约4.2%。而三角形微织构轴承承载力随微织构深度变化趋势与其余形状不同,关于三角形微织构没有提升承载力的原因在后文进行研究。

图4 不同形状微织构轴承承载力随微织构深度的变化
图5所示为不同微织构深度下,7种不同形式微织构气体箔片轴承的摩擦力矩变化曲线。可以看出,随着微织构深度的增加,轴承摩擦力矩呈现先减小后增大的趋势,其中矩形微织构降低轴承摩擦力矩的效果最好。
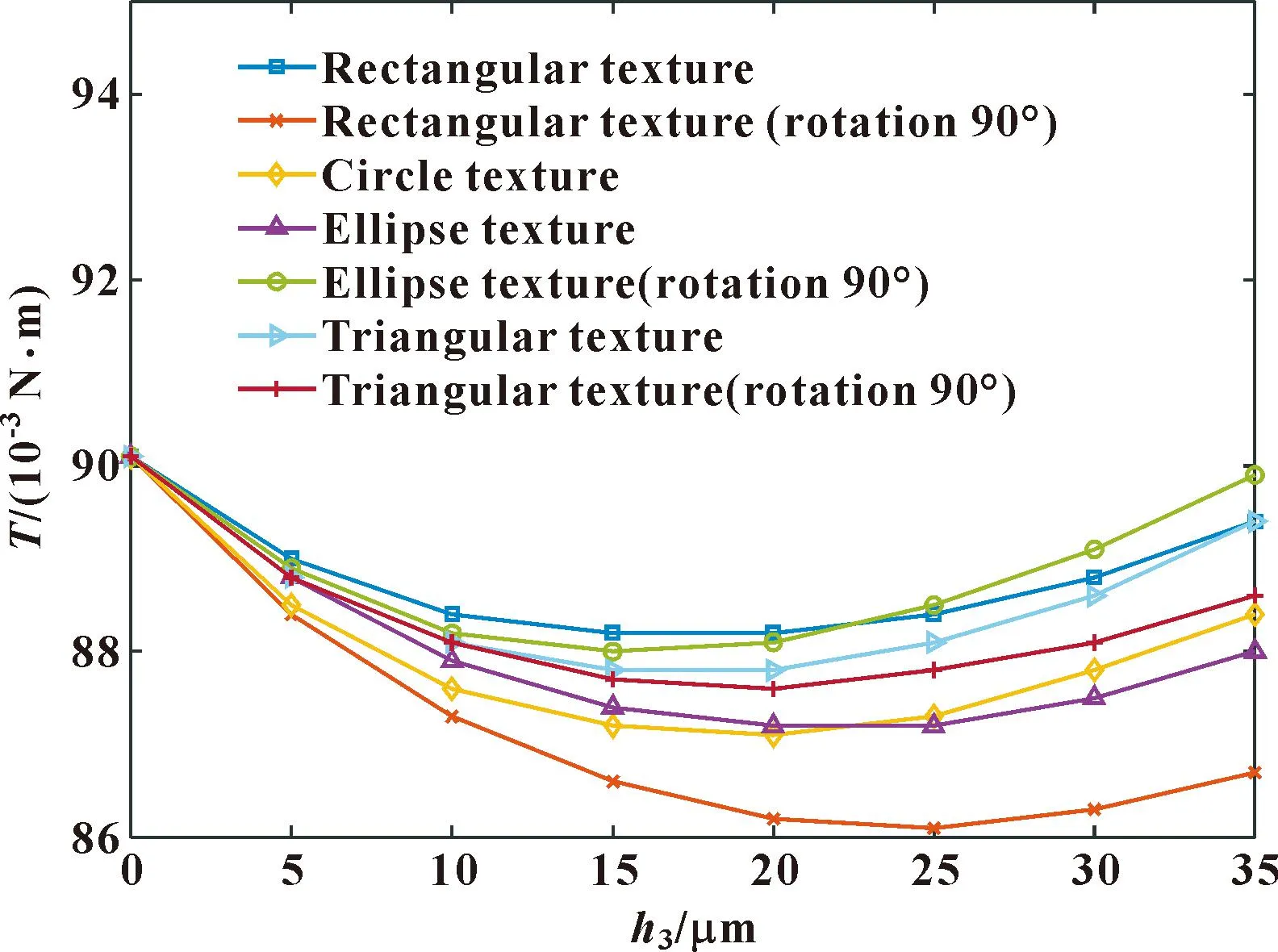
图5 不同形状微织构轴承摩擦力矩随微织构深度的变化
为提高轴承性能,在提高轴承承载力的同时还应降低其摩擦力矩。当微织构深度达到35 μm时,相比于无微织构轴承,椭圆形微织构轴承承载力提升了约4.2%,摩擦力矩降低了2.3%,矩形(旋转90°)微织构承载力提升了1.3%,摩擦力矩降低了3.7%。综合比较,椭圆形微织构对轴承性能的提升效果相对较好。
为进一步研究径向微织构气体箔片轴承承载力增大的机制,对以3种织构形式轴承的气膜压力进行了对比,结果如图6所示。从图6(b)可看出,椭圆形微织构气体箔片轴承的气膜压力在峰值区域出现压力波动,该波动可认为是微织构提升流体动压润滑效果的体现,动压效应提高了轴承的平均压力和最大气膜压力,进而提高了轴承的承载力;椭圆形织构使得压力沿着周向方向扩散,使得负压区压力增大,因此椭圆形微织构承载力优于其他形状。三角形微织构加入轴承平箔片后会降低轴承的承载力,从图6(c)所示的压力分布可看出,气膜压力的负压区范围增大(图中红色圆圈部分),轴承平均气膜压力和最大气膜压力减小,无法提高轴承承载力。

图6 不同织构轴承量纲一气膜压力分布
3.2 微织构参数对气体箔片轴承性能的影响
上一节研究结果表明,椭圆形微织构润滑性能要优于其他形状微织构。下文以椭圆形微织构径向气体箔片轴承为研究对象,对微织构其他参数进行研究。
3.2.1 微织构深度的影响
不同微织构深度的轴承的承载能力和摩擦力矩如图7所示。可以看出,轴承的承载力和摩擦力矩随着微织构深度的增加呈现出先减小后增大的趋势。进一步探究微织构深度的影响机制,对不同深度下轴向中截面的量纲一压力进行比较,如图8所示。
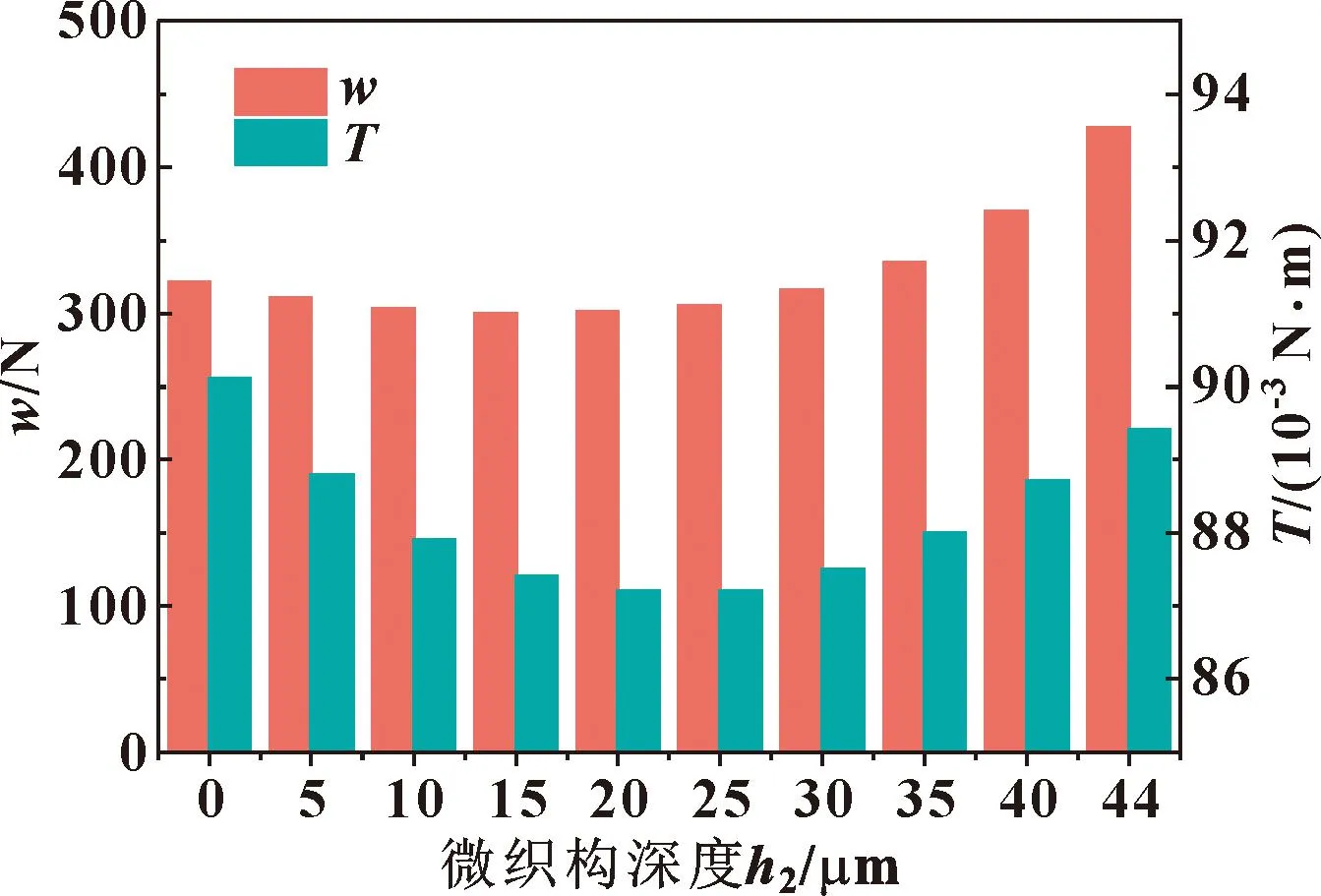
图7 不同微织构深度下轴承的承载力和摩擦力矩
由图8可知,当微织构深度低于35 μm时,气膜压力虽有波动,但波动始终围绕无微织构时的压力值,该波动不会使气膜压力整体增大,会使轴承的承载力下降;当微织构深度超过35 μm后,压力波动变大,使得轴承整体气膜压力变大,提高了轴承的承载力;当微织构深度超过44 μm以后,仿真结果显示,轴承的气膜压力不收敛,可能是由于微织构产生的气膜波动过大,破坏了气膜的稳定性,可见微织构深度不是越大越好。
3.2.2 微织构数量的影响
上述研究表明,当微织构深度在一定范围内时,对改善轴承的静态特性起着重要作用。在该深度范围内,研究了微织构数量对轴承静态特性的影响。
图9和图10示出了微织构数量对轴承静态特性的影响。当微织构数量从 108增加到300时,轴承的承载力和摩擦力矩的变化比较平稳,说明微织构数量对气体箔片轴承静特性的影响较小。综合比较,当微织构数量为24×8,微织构深度为44 μm时,轴承的性能相对最优,此时承载力提升了32.47%,摩擦力矩降低了0.78%。
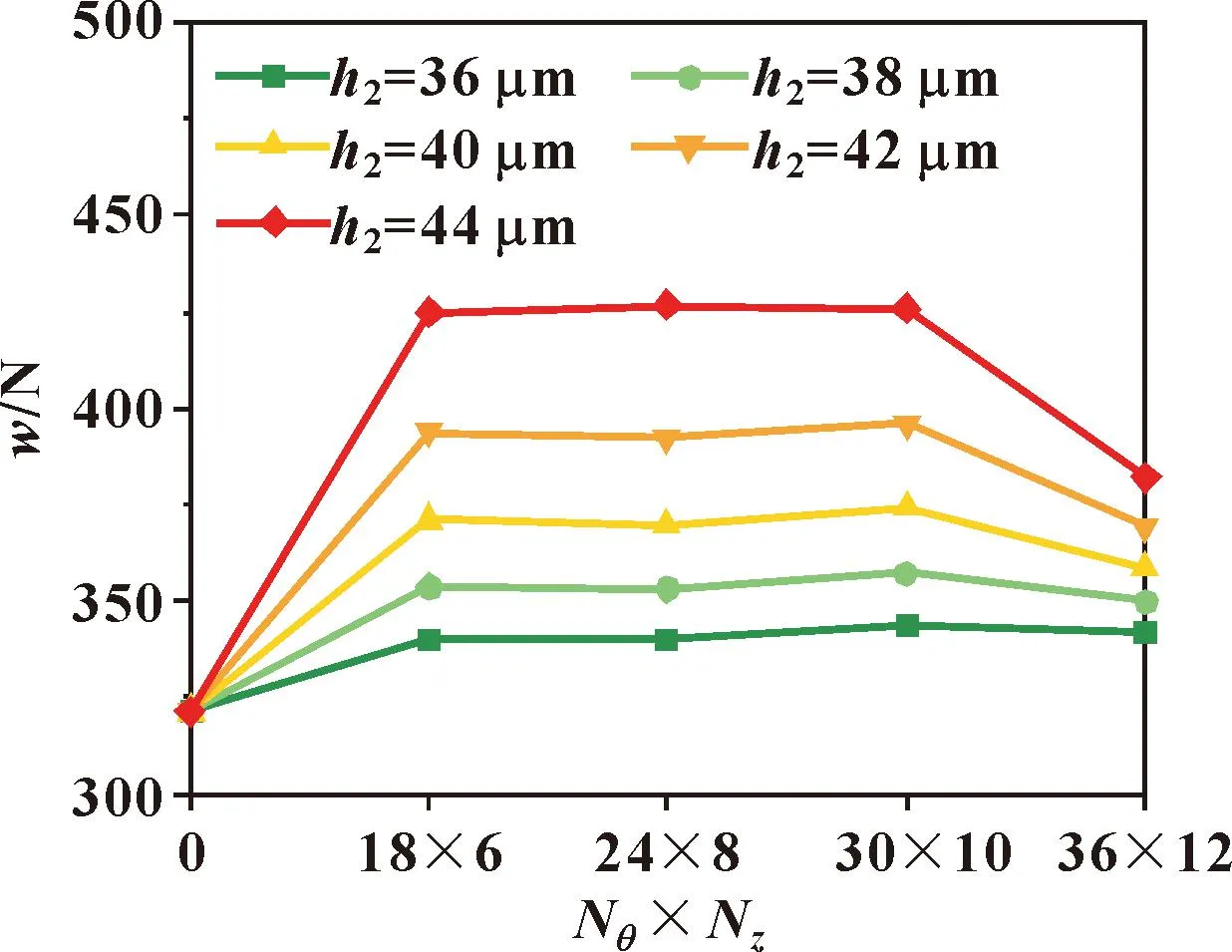
图9 不同微织构深度下承载力随微织构数量的变化
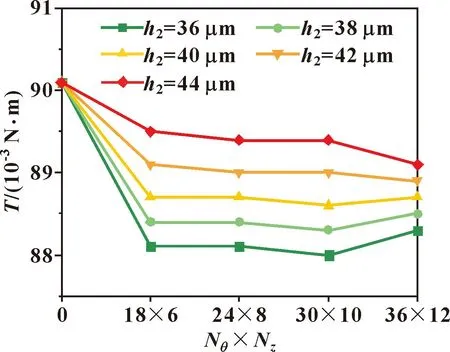
图10 不同微织构深度下摩擦力矩随微织构数量的变化
3.2.3 微织构占比的影响
微织构占比指的是微织构总面积在轴承平箔片总面积中所占的比例。图11示出了承载力和摩擦力矩随微织构占比的变化。可以看出,随着微织构占比的增加,承载能力趋于增加,摩擦力矩大致趋于减少。当微织构数量为24×8,微织构占比为0.25,微织构深度为44 μm时,承载能力增加了36.32%,摩擦力矩减少了1.66%。
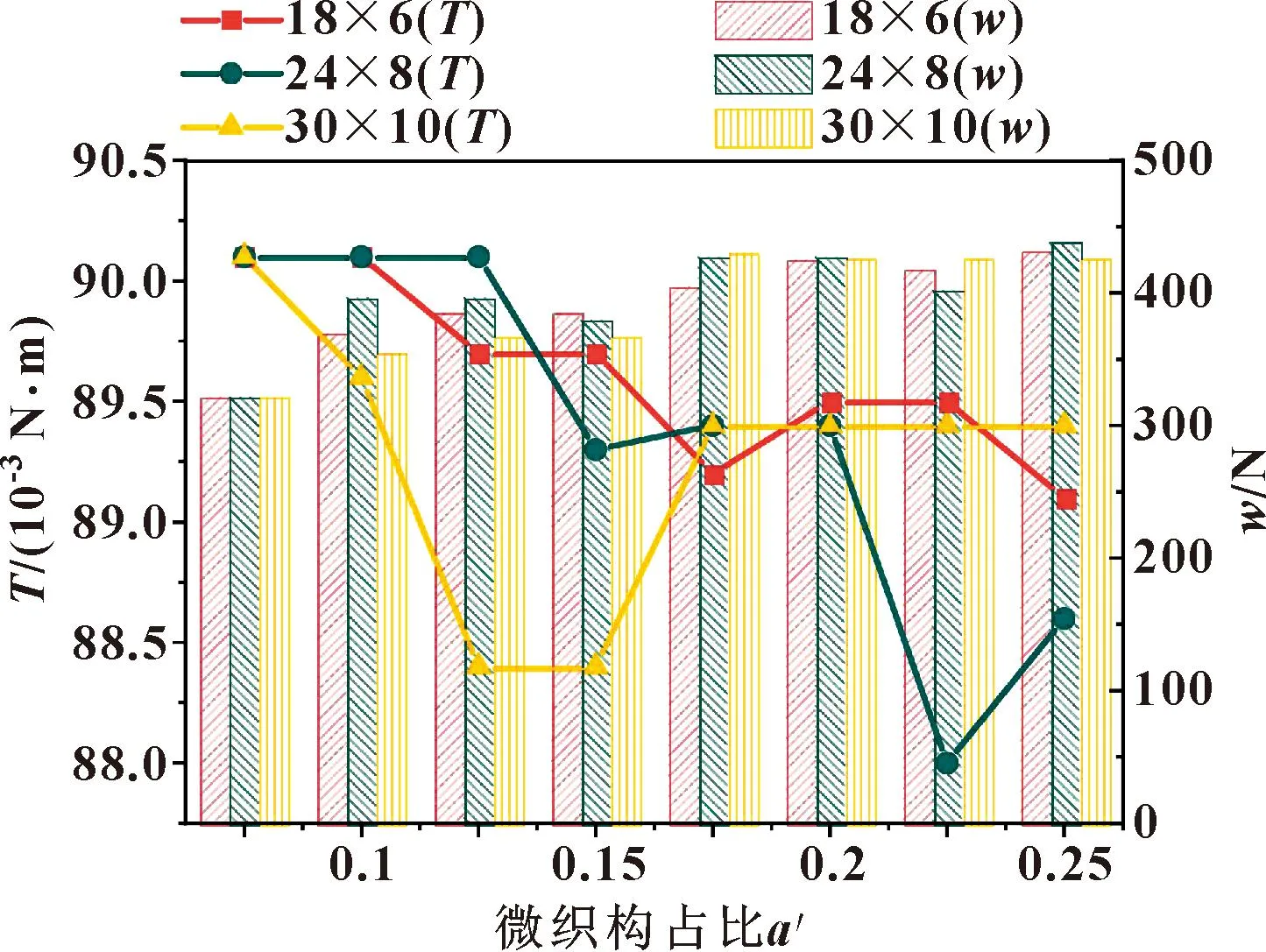
图11 承载力和摩擦力矩随微织构占比的变化
3.3 表面粗糙度对气体箔片轴承性能的影响
前文研究表明,当微织构数量为24×8,微织构占比为0.25,微织构深度为40 μm时,轴承性能有较好的改善。基于上述微织构参数,引入高斯粗糙表面,改变粗糙表面的参数,对轴承性能进行了分析。如表4所示,各向异性的高斯粗糙表面能够更好地模拟车削过程形成的粗糙表面。βx和βy分别是x和y方向的自相关长度,当βx=βy时,粗糙表面是各向同性的,当βx≠βy时,粗糙表面是各向异性的。
图12和图13所示分别是椭圆形微织构轴承和无微织构轴承的承载力和摩擦力矩随均方根粗糙度σ的变化。可以看出,粗糙度对微织构轴承和无微织构轴承的摩擦力矩影响趋势大致相同,但对两者承载力的影响存在区别。总体来说,粗糙表面对轴承性能的影响不容忽视,在微织构气体箔片轴承的模型中考虑粗糙度是很有必要的。
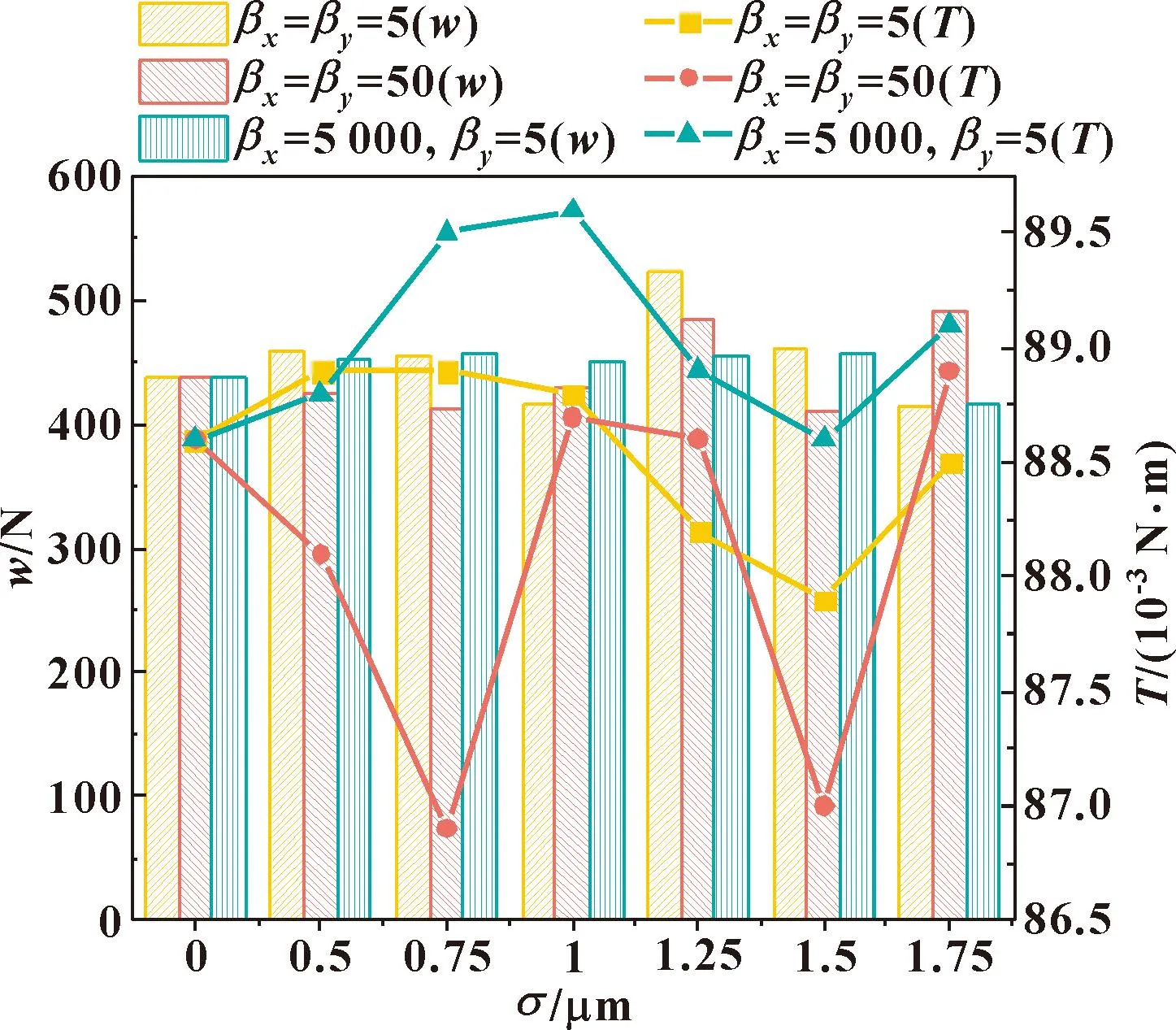
图12 粗糙度对微织构轴承承载能力和摩擦扭矩影响
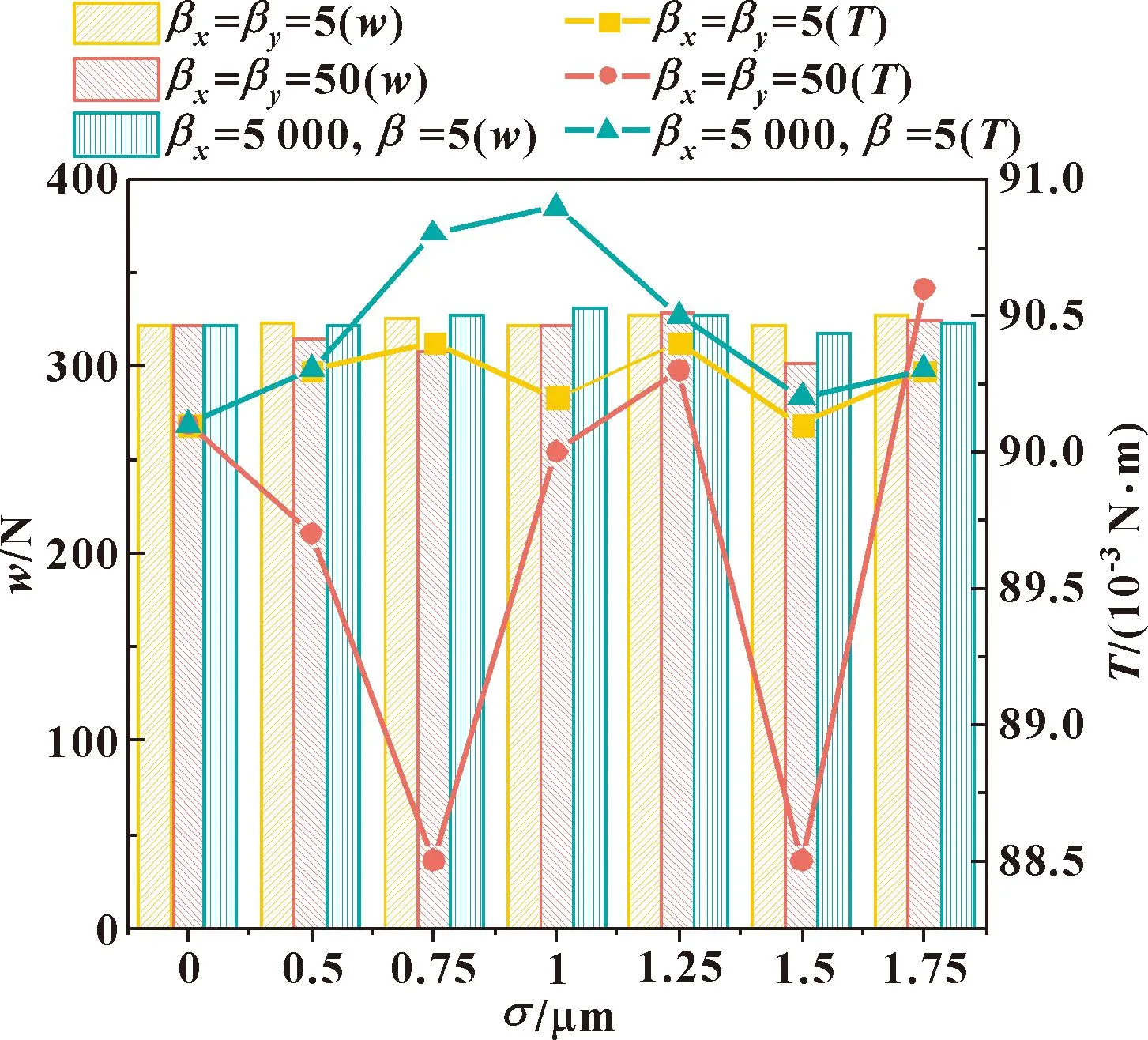
图13 粗糙度对无微织构轴承承载力和摩擦力矩的影响
图14和15所示分别为考虑自相关长度βx=5 000、βy=5、σ=2 μm的高斯随机粗糙表面的微织构轴承的气膜厚度和压力分布。从图14中可以看出,由于实际加工形成的车削纹路,反映在气膜厚度中会产生条状波动,叠加微织构的影响后沿轴向的气膜厚度波动更加明显。从图15中可以看出,考虑粗糙表面的微织构气体箔片轴承的气膜压力分布也相应发生变化,压力峰值分布相较于不考虑粗糙度时更加分散,轴承端部压力明显提高。
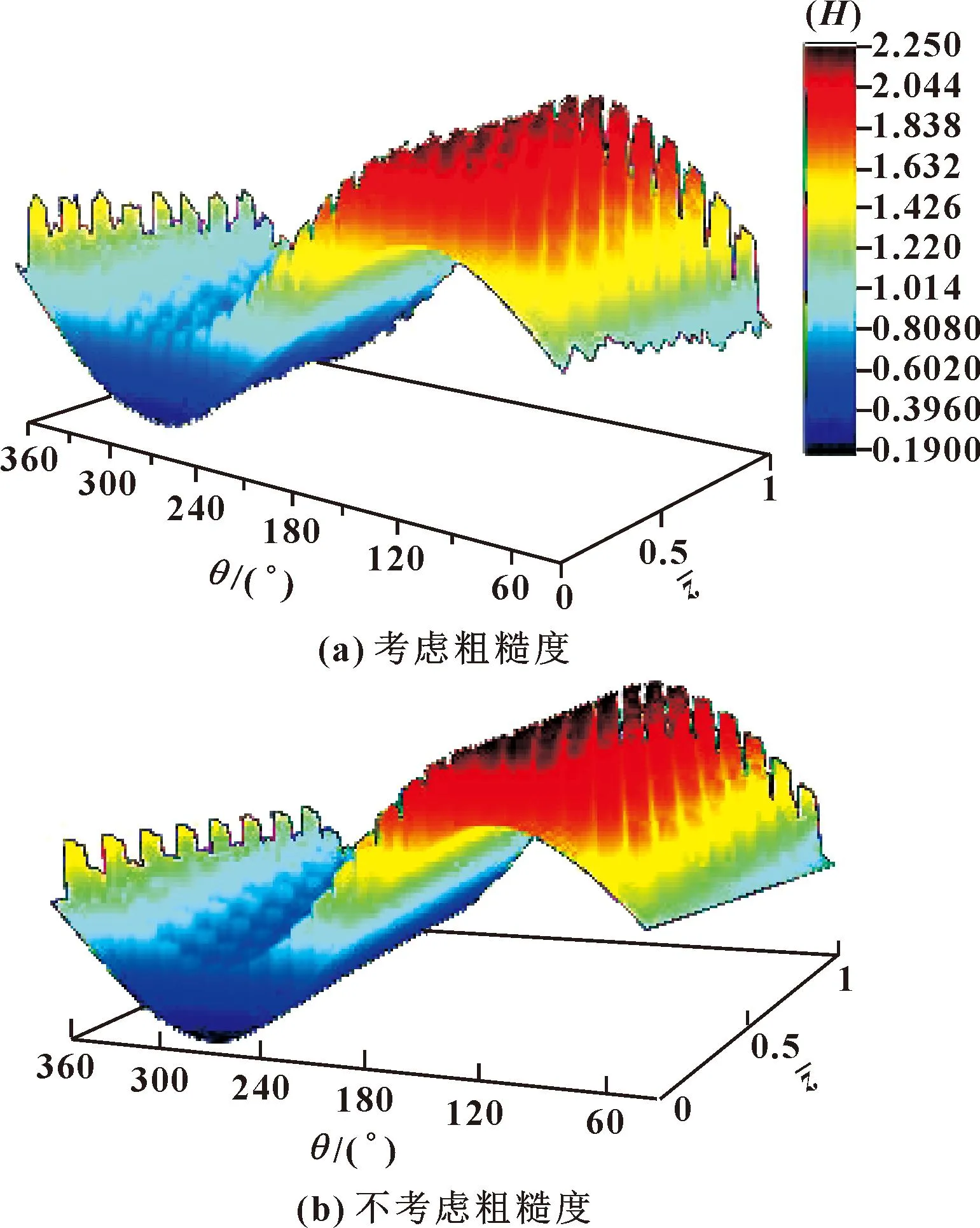
图14 量纲一气膜厚度分布
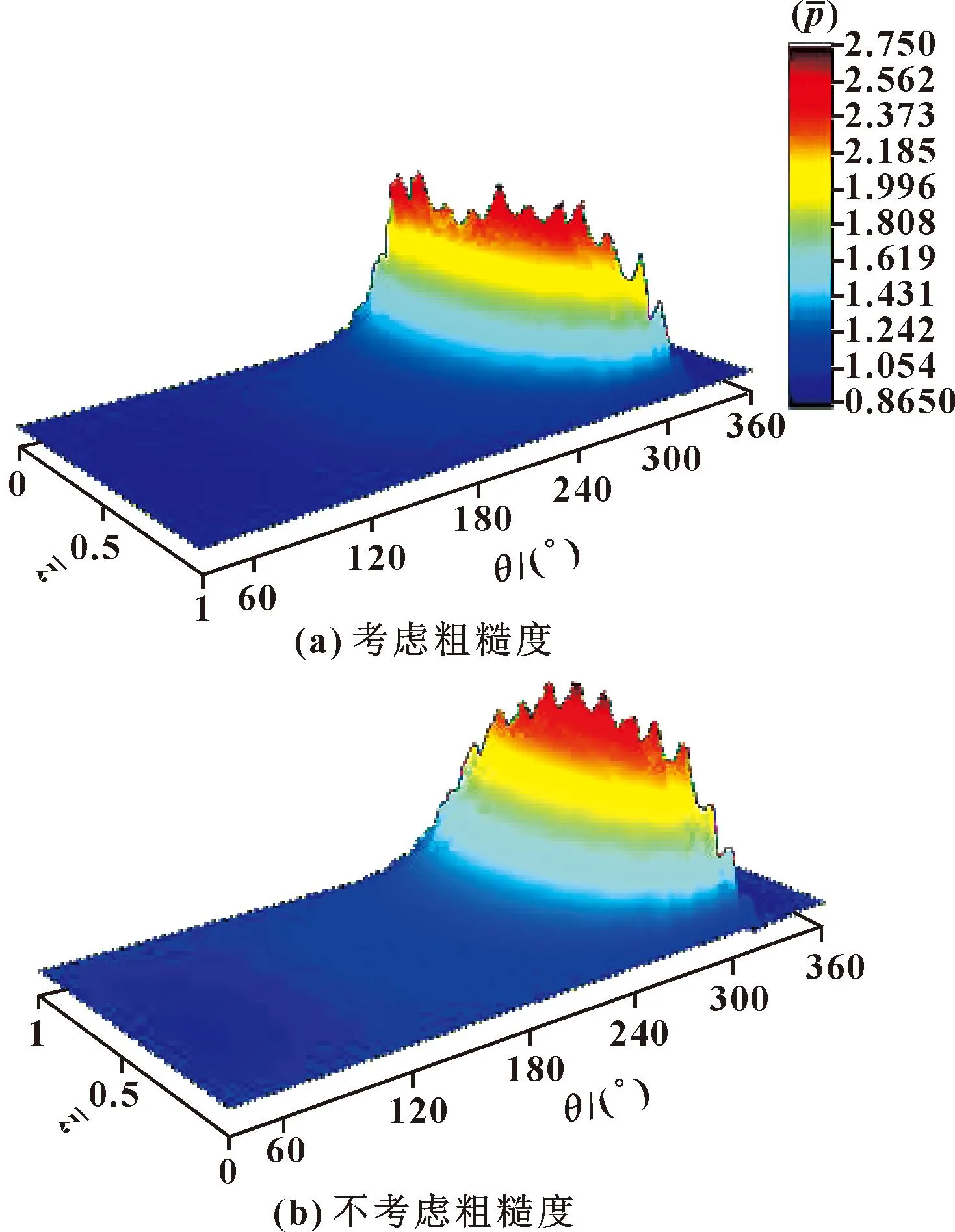
图15 量纲一压力分布
4 结论
(1)不同形式的微织构对轴承性能有不同的影响。其中,椭圆形织构对改善轴承的静态特性最为有效。由于椭圆形织构的分布使压力沿圆周方向传播,负压区的压力增大,提高了轴承的平均压力和最大气膜压力,进而提高了轴承的承载能力。
(2)只有在微织构深度达到一定范围后,改变微织构深度才能起到改善轴承性能的作用。微织构数量的变化对轴承的静态特性影响不大。在一定范围内,轴承的静态特性随着微织构占比的增加而提升。与无微织构的传统轴承相比,优化的织构参数可使径向气体箔片轴承的承载能力提高36.32%,摩擦力矩降低1.66%。
(3)与不考虑粗糙度的情况相比,考虑粗糙表面的微织构径向气体箔片轴承的压力峰值分布更加分散,轴承端部的压力明显提高。
