多叶箔片气体动压轴承静态特性研究
2023-10-17刘恒贾晨辉刘书明李东东张飞
刘恒,贾晨辉,刘书明,李东东,张飞
(河南科技大学 机电工程学院,河南 洛阳 471003)
箔片气体轴承具有无污染,自适应能力强,使用寿命长和运行稳定性良好等诸多优点,广泛应用于低温工程、国防和航空航天等领域,并发挥了重要作用[1-2]。箔片气体轴承分为波箔型和多叶型(悬臂型)轴承等,多叶型轴承结构简单,加工工艺要求低,广泛应用在高速旋转的小型轻载机械上。
文献[3]通过引入辅助分析部件的方法,建立了含有大预紧效应的多叶箔片轴承的非线性接触模型,并将其进行完全的气弹耦合求解,结果表明此方法收敛性较好,并能很好地解决弹性箔片的非线性大变形扭曲和复杂载荷情况下的预紧问题。文献[4-5]将多叶箔片轴承结构用到油润滑箔片轴承中,搭建了针对多叶箔片轴承的试验台,对五叶片油润滑的箔片轴承进行试验,在转速30×103r/min时轴承仍能稳定运转,说明油润滑箔片轴承在高速运行时表现良好,具有较好的抵抗冲击能力以及良好的稳定性和适应能力。文献[6]将多叶箔片油润滑轴承的刚度引入到轴承转子系统中,分析了轴承动态刚度对轴承转子系统的影响,并搭建试验台验证其结果,结果表明多叶箔片油润滑轴承对转子的升速适应能力强。文献[7-9]提出一种带弹性支持结构的油润滑多叶箔片轴承,通过卡氏定理建立多叶箔片的变形模型对其进行求解,并搭建多叶箔片油润滑轴承的试验台,试验结果表明带弹性支持结构的轴承承载力、稳定性都优于无弹性支持结构的轴承。文献[10]通过试验研究含波箔的四叶箔片轴承,提出一种确定刚度系数和阻尼系数的频域识别方法。文献[11-12]采用悬臂梁模型建立了考虑相邻箔片面接触的动力学模型,运用有限元法与加权余量法对雷诺方程进行耦合求解,并提出一种判断相邻箔片是否接触的算法,但计算量大,会出现难收敛的问题,对网格划分要求较高,而且未考虑预紧力对轴承性能的影响。随着研究的深入,文献[13]利用有限元法对新型三瓣式箔片轴承展开研究,分析了接触面间库伦摩擦力下预载和安装角度对轴承静动态性能的影响,发现预载能提高轴承的承载能力,且转速越高承载能力越大。文献[14]研究润滑剂和热蠕变对气体轴承的影响,结果表明选择摩尔质量大的气体能提高轴承的稳定性和承载能力;相对于没有热蠕变的情况,有热蠕变对气体轴承的稳定性破坏明显,但对承载能力有一定的提高。文献[15]研究箔片厚度对波箔型气体动压轴承承载力的影响,结果表明箔片厚度与轴承承载力成反比。
文献[4-9]针对多叶箔片油润滑轴承进行研究,但未对箔片厚度、轴承间隙进行研究;文献[11-12]未考虑预变形对多叶箔片气体轴承性能的影响。轴承结构对多叶箔片气体轴承性能影响的文献较少,基于文献[13-15]研究的轴承结构对波箔型气体轴承性能的影响,本文针对有预变形的多叶箔片气体动压轴承,通过理论计算研究多叶箔片气体动压轴承静态特性,分析轴承结构和运行参数对承载力的影响,为应用箔片气体动压轴承及优化其结构提供参考。
1 理论分析
如图1所示,多叶箔片气体动压轴承由弹性支承和轴承座构成,弹性支承与转子之间形成收敛楔。弹性支承由若干个箔片或箔片组件顺次搭建构成,且箔片或箔片组件的一侧通过插槽固定在轴承座上,箔片的另一侧搭接在其他箔片上。在多叶箔片轴承工作过程中,轴承的气膜压力会导致箔片形状发生变化,从而影响气膜厚度,最终导致气膜压力的变化。

图1 多叶箔片气体动压轴承实物图
1.1 控制雷诺方程
多叶箔片气体动压轴承的气膜间隙远小于转子半径,可以把轴承沿周向展开建立坐标系,x为周向,z为轴向,y为气膜厚度方向,如图2所示。

图2 多叶箔片气体动压轴承气膜展开图
稳态时雷诺方程为
(1)
式中:p为气体压力;h为气膜厚度;η为气体动力黏度;R为转子半径;ω为轴径角速度。
(2)
(3)
式中:L为轴承长度;p0为环境气压;C0为轴承半径间隙;Λx为轴承数。
1.2 气膜厚度模型
箔片装配完成后假定箔片与箔片、转子与箔片为线接触且无作用力,在安装前后箔片的曲率半径保持不变,而且在装配过程中箔片不变形。
多叶箔片的几何关系如图3所示,A为箔片内表面的末端点,B为转子与箔片的接触点,C为箔片内表面上任意一点,D为相邻箔片接触点,O为轴承中心,O′为箔片圆心。
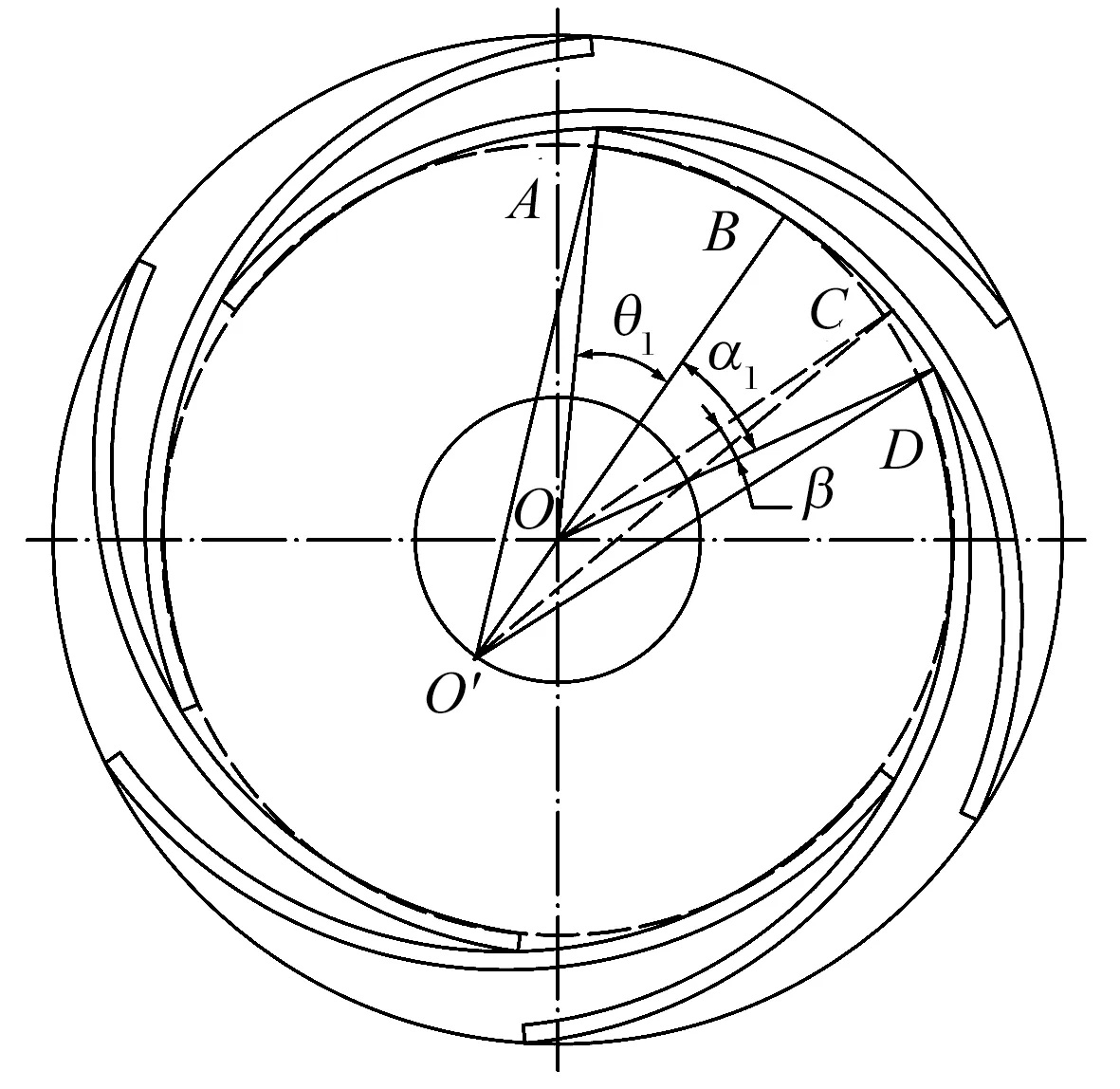
图3 多叶箔片的几何关系
在不偏心时箔片与转子相切,此时箔片沿周向均匀分布,可得如下关系
(4)
根据余弦定理,在△OO′D和△OO′A中可得到如下关系
(5)
式中:n为箔片数量;Rg为箔片曲率生成圆半径;ρ0为箔片内表面曲率圆半径;Ra为箔片内表面的末端点A构成的圆半径;t为箔片厚度。
已知t,Rg,R,根据(4)—(5)式可计算Ra,α1,θ1的值。
根据余弦定理,在△OCO′中可得到如下关系
(6)
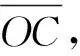
(7)
当箔片受预紧力影响时,箔片会发生变形,变形尺寸远小于箔片尺寸,因此可按照径向变形计算。箔片初始预变形采取悬臂梁模型如图4所示。

图4 箔片悬臂梁示意图
A点、B点和D点的变形分别表示为[16]
(8)
式中:n1,n2分别为单位宽度上A点、D点受到的接触力;f为单位宽度上B点受到的预紧力;ΔB为箔片与转子接触点的初始预变形(ζ);ΔA和ΔD为该箔片与相邻箔片的接触点(接触点在该箔片上)发生的变形;E为弹性模量;I为惯性矩。
由箔片对称可得
ΔA=ΔD,
(9)
n1=n2。
(10)
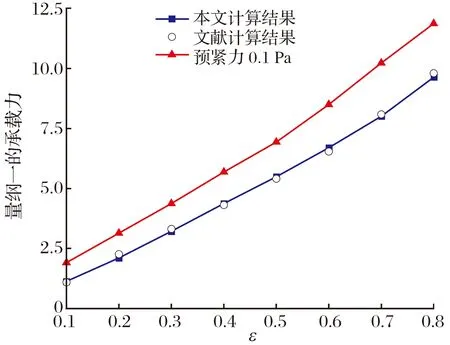
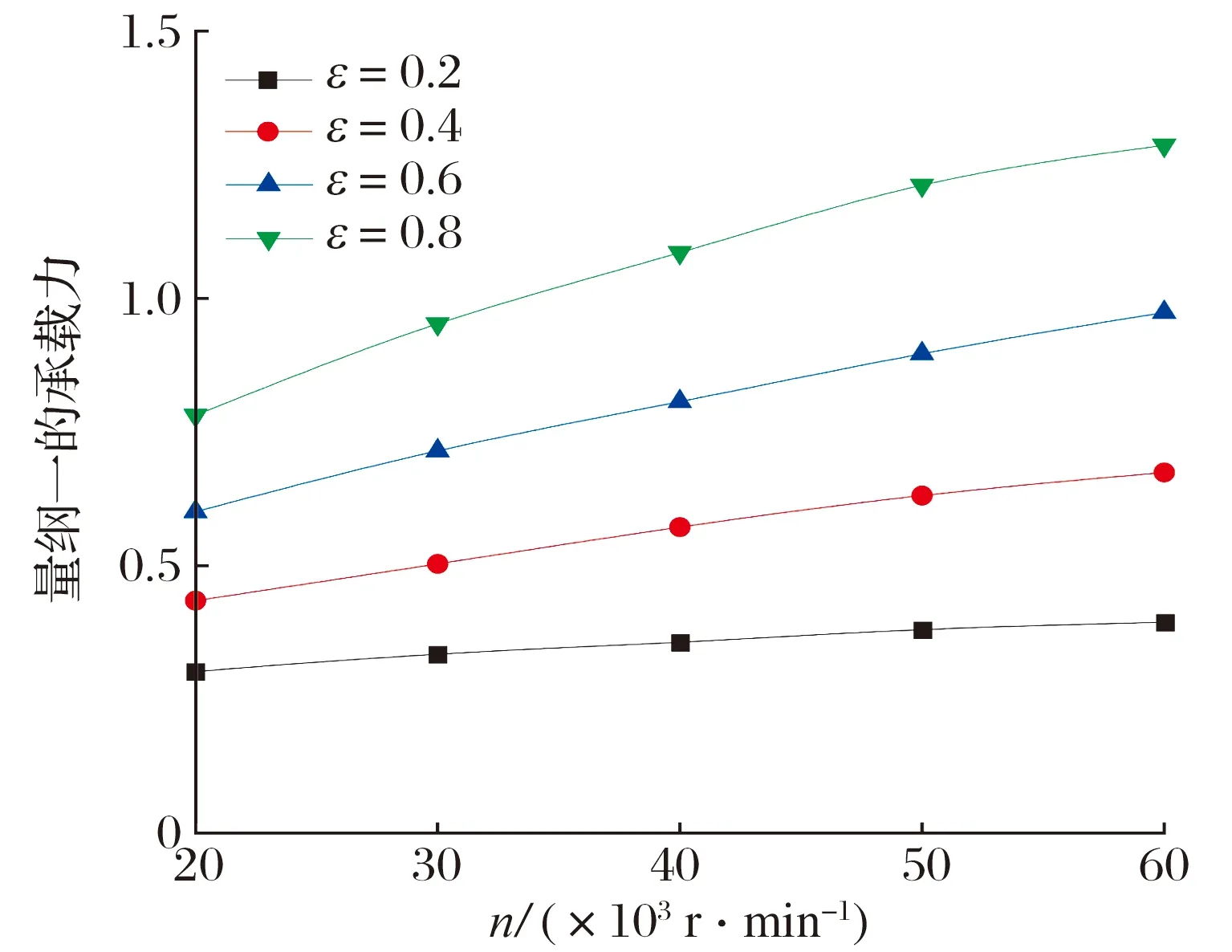
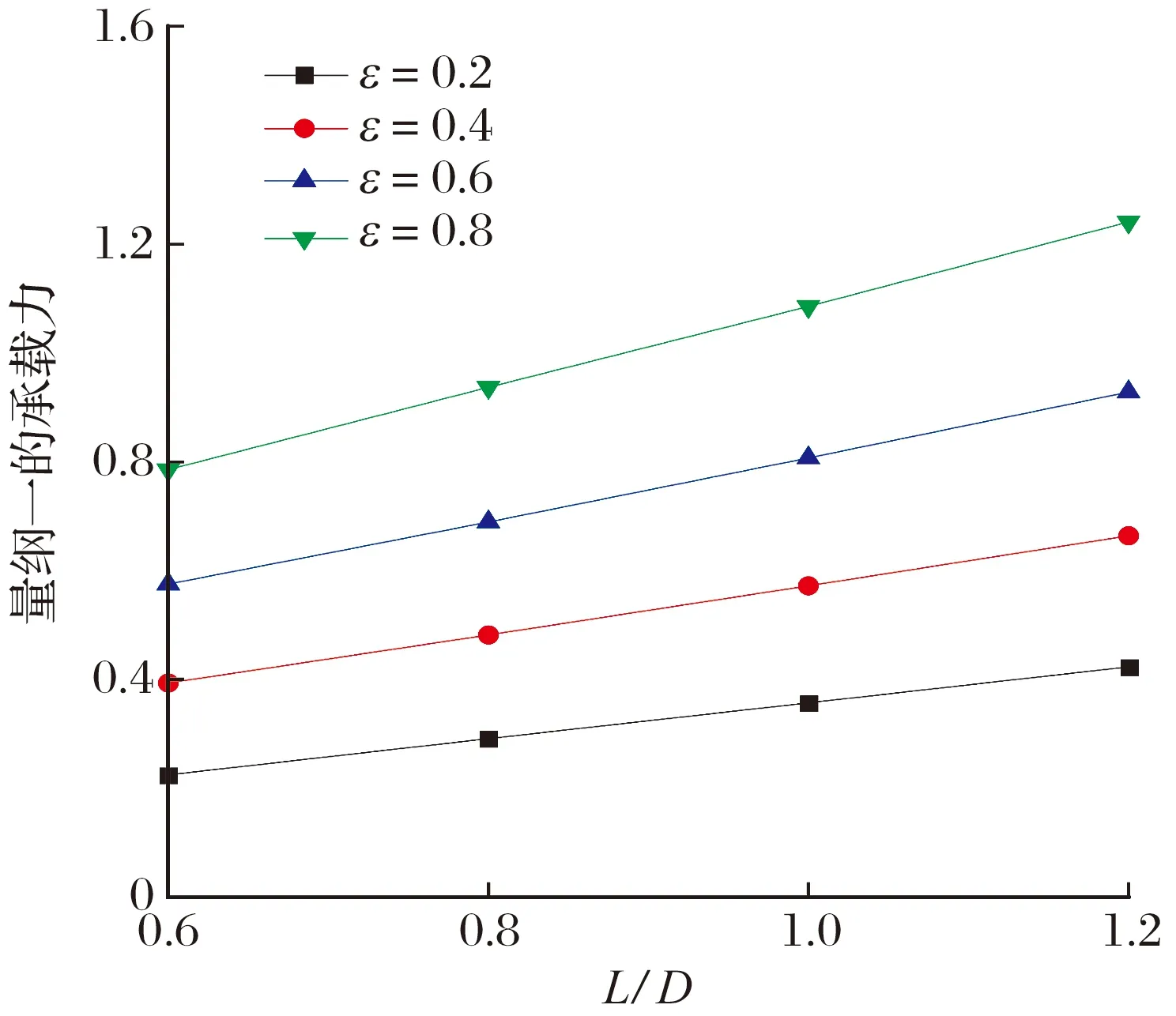
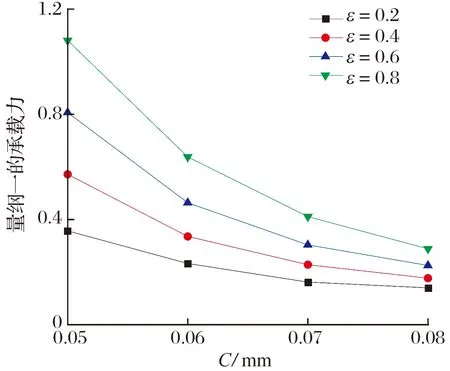
由 (8)—(10)式可求出f,则可求任意一点C的变形。当C点在B点与D点之间,即x (11) 当C点在A点与B点之间,即x≥b时 (12) 则初始气膜厚度修正为 (13) 根据多叶箔片气体动压轴承结构,把箔片简化为悬臂弯曲梁,并假定相邻箔片之间无摩擦。因此,每个箔片只承受径向力,在变形小的条件下,可利用卡氏定理计算箔片的变形。如图5所示,当节点s受到单位法向力F作用时,节点u的径向位移(柔度系数)U(K,Ψ)可表示为[12] 图5 箔片变形图 U(K,Ψ)= (14) 式中:K为节点u的圆心角;Ψ为节点s的圆心角。 将箔片简化为悬臂弯曲梁,研究对象为箔片中任意一个箔片,其受力如图6所示。箔片i的受力状态为箔片i-1的接触力Fi-1、箔片i+1的接触力Fi+1以及箔片i上节点j受到的气膜力Pi,j。Φ为箔片的包角,θi,N为任一点N和O点连线与箔片固定端的夹角,α为箔片重叠区的角度,θi,j为气膜力Pi,j与固定端的夹角。 图6 箔片受力图 两箔片的接触点A在箔片i上的径向位移为 FiU(Φ,Φ), (15) 同理接触点A在箔片i+1上的径向位移为 Fi+1U(α,Φ), (16) 由于箔片i与箔片i+1在A点接触,所以 δi,A=δi+1,A, (17) 化简可得 -Fi-1U(Φ,α)+Fi[U(α,α)+U(Φ,Φ)]- (18) 本文研究的多叶箔片气体动压轴承有6个箔片,按照i=2→6→1的顺序书写矩阵,即 AF=PU, (19) F=[F1F2F3F4F5F6]T, 式中:A,U为柔度矩阵;F为节点接触力矩阵;P为气膜压力矩阵。 由(19)式求出箔片间的作用力,即可得到整个箔片的受力状态,进而得到箔片所有点变形的大小,选择箔片i为研究对象,则任意点N的位移为 δi,N=-Fi-1U(θi,N,Φ)+FiU(θi,N,α)- (20) 轴承正常运行时气膜厚度由转子的偏心量、气膜厚度的初始量以及箔片变形量构成,则气膜厚度为 h=h0+ecos(θ-φ0)+uf, (21) 式中:h0为初始气膜厚度;e为偏心量;θ为气膜圆周方向坐标;φ0为偏位角;uf为箔片的变形量。 将牛顿-拉弗森迭代公式代入(3)式中并化简得 (22) 各阶中心差分得 整理得 Ai,jδi-1,j+Bi,jδi+1,j+Ci,jδi,j-1+Di,jδi,j-1+ Ei,jδi+1,j=-Fi,j, (23) 多叶箔片气体动压轴承每个箔片的边界条件都相同,可先通过单独求解每个箔片,然后通过整体组装计算轴承的静态特性。对箔片进行网格划分,如图7所示。 图7 箔片的网格划分 轴承轴向两端与大气相通,且轴承相邻箔片搭建处最小气膜厚度远小于箔片厚度,所以可将箔片搭建处和轴承轴向两端的压力等同于大气压力。则环境边界条件为 p=p0, (24) 计算区域取轴向的一半,则气压变化梯度在中间轴面时为零,则对称边界条件为 (25) 收敛条件为 (26) 气压分布会引起箔片变形,箔片变形会改变膜厚的分布,进而改变气压分布,将气压分布和箔片变形不断进行迭代求解,当满足收敛条件时,计算停止。数值计算流程如图8所示。 为确定计算以及程序编写的准确性,采用本文方法计算不考虑预紧力以及预紧力为0.1 Pa时文献[17]中多叶箔片气体动压轴承的承载力,结果如图9所示:当不考虑预紧力时,本文理论计算的承载力与文献计算的基本一致,验证了本文方法的正确性以及程序编写无误。在预紧力为0.1 Pa时,轴承承载力比无预紧的大,因为预紧力会使箔片在轴承工作前发生变形,承载力会有所增大,与实际一致。因此本文计算模型正确。 图9 本文与文献[17]轴承承载力的计算结果对比 本文计算的多叶箔片气体动压轴承的结构和其他参数见表1。 表1 多叶箔片气体动压轴承结构和其他参数 当偏心率ε为0.2,转速n为40×103r/min时,多叶箔片气体动压轴承气膜压力和气膜厚度的分布如图10所示: 气膜压力和气膜厚度中出现了6个明显的波谷和波峰,且箔片3和箔片4压力明显大于其余箔片的,这主要是由于偏心的作用,轴承主要承载区在箔片3和箔片4处,且对应的气膜厚度最小。 图10 量纲一的气膜压力和气膜厚度 转速和偏心率对轴承承载力的影响如图11所示,当偏心率不断增大时,承载力也将增大,且转速越高承载力越大。这是由于转速升高会导致气体流速变快,进而增强了轴承的气体动压效应,气膜压力变大,所以承载力增大。 图11 转速和偏心率对轴承承载力的影响 当偏心率不变时,若使轴承结构的几何尺寸不变,仅箔片厚度变化,相当于对轴承预紧。因此本文保持轴承结构的几何尺寸不变,让箔片厚度与轴套内半径Rb对应变化,具体见表2。 表2 箔片厚度与轴套内半径的对应关系 箔片厚度对轴承承载力的影响如图12所示,当偏心率为0.2和0.4时,承载力随箔片厚度的增大而增大,且箔片厚度超过0.10 mm时,承载力的增大量越来越小,这是因为当箔片厚度增大时,箔片刚度将会增大,有利于承载;当偏心率超过0.6时,随着箔片厚度逐渐增大,承载力呈先增大后基本不变或减小的趋势,且拐点在箔片厚度为0.10 mm时,这是因为箔片厚度增大导致轴承气膜厚度增大,进而使承载力减小。由计算结果可知,箔片厚度选取0.10 mm,有利于轴承承载。 图12 箔片厚度对轴承承载力的影响 综上所述,箔片厚度增大的同时使箔片支承刚度和气膜厚度增大,这2种效果的共同作用影响承载力大小。当偏心率为0.2和0.4时,箔片厚度增大使支承刚度变大占主导;当偏心率超过0.6时,箔片厚度增大使气膜厚度增大占主导。 转子直径D为定值,通过改变轴承长度L使长径比L/D为0.5~1.2。长径比对轴承承载力的影响如图13所示,当偏心率不变时,随着轴承长径比的不断增大,承载力也会增大。这是由于当轴承的长径比不断增大时,有效的轴承承载区域会变大,会使承载力增大。但长径比增大对提高承载力的作用较小,当长径比从0.6增大至1.2,即长径比增大1倍时,承载力将提高0.5倍左右。 图13 长径比对轴承承载力的影响 保持轴承其他结构不变,轴承间隙C的大小仅由轴套内半径决定(C=Rb-R-2t),具体见表3。 表3 轴承间隙与轴套内半径的对应关系 轴承间隙对轴承承载力的影响如图14所示:当偏心率不变时,随着轴承间隙的不断增大,轴承承载力减小,这是因为当轴承间隙增大时,气膜厚度增大,进而使动压效应减弱,承载力减小;当偏心率为0.8,轴承间隙从0.05 mm增大到0.06 mm时,承载力减小40%,轴承间隙从0.07 mm增大到0.08 mm时,承载力减小28%。说明多叶箔片轴承的间隙越小,越有利于轴承动压效应的产生。因此可通过减小轴承间隙来增大轴承的承载力,但轴承间隙减小时,会导致轴承启停时摩擦增大,进而影响轴承寿命。 图14 轴承间隙对轴承承载力的影响 轴承预变形对轴承承载力的影响如图15所示: 当偏心率不变时,轴承预变形可使其承载力增大,且随偏心率不断增加时,预变形越大承载力的差值越大。这是由于轴承在预紧时会使箔片在轴承工作前发生变形,有利于提高箔片的刚度。 图15 轴承预变形对轴承承载力的影响 建立了箔片含有预变形的多叶箔片气体动压轴承计算模型,采用牛顿-拉弗森迭代法以及有限差分法对雷诺方程和气膜厚度方程进行求解,研究转速、偏心率、箔片厚度、长径比、轴承间隙以及预变形对轴承承载力的影响,得到以下结论: 1)随着偏心率的不断增大,轴承承载力不断增大,且转速越高承载力越大;偏心率相同时,随着轴承长径比的不断增大,承载力不断增大,但增幅不明显。 2)当偏心率小于0.6时,轴承承载力随箔片厚度增大而增大;当偏心率大于0.6时,轴承承载力拐点出现在箔片厚度为0.10 mm处,此时承载力最大。 3)可通过减小轴承间隙提高轴承承载力,但轴承间隙小时启停摩擦会增大,影响轴承寿命,应慎重选择;当偏心率相同时,预变形越大越有利于提高轴承承载能力。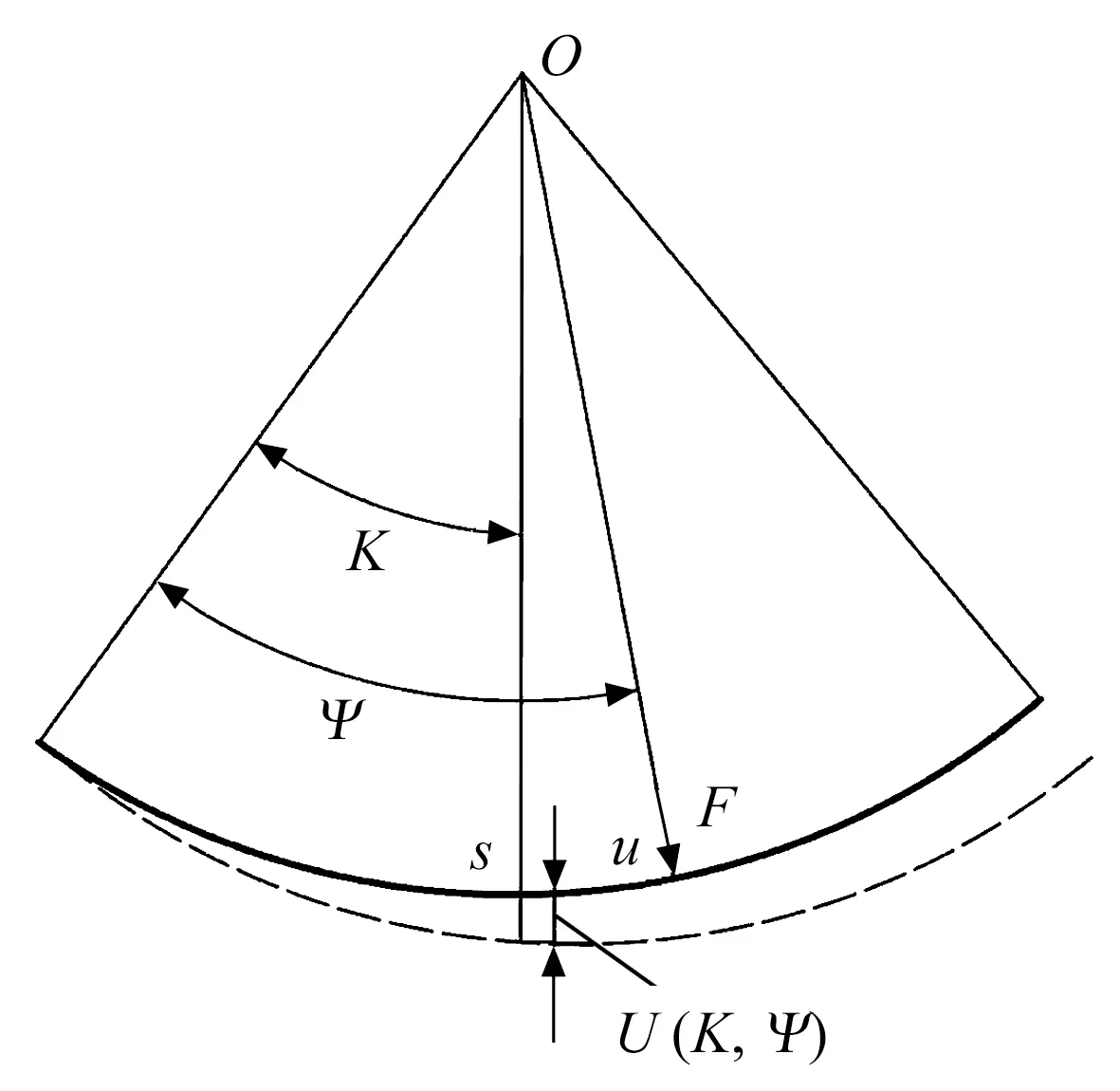

1.3 离散雷诺方程
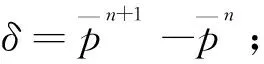
1.4 网格划分及边界条件

1.5 计算流程
2 计算程序验证
3 结果分析
3.1 多叶箔片气体动压轴承气膜压力的分布

3.2 转速和偏心率的影响
3.3 箔片厚度的影响


3.4 长径比的影响
3.5 轴承间隙的影响

3.6 轴承预变形的影响

4 结论
