电力电子组网系统中构网型换流器间的协同限流研究
2024-04-17孟建辉赵鹏飞周靖皓
刘 宝, 孟建辉, 王 毅, 赵鹏飞, 郭 锋, 周靖皓
(1.新能源电力系统国家重点实验室(华北电力大学),河北 保定 071003;2.国网台州供电公司,浙江 台州 318099;3.国网浙江省电力有限公司,浙江 杭州 310063)
0 引 言
在国家能源转型及“双碳”目标的背景下,光伏、风电等新能源发展迅速,电网将呈现高比例新能源和高比例电力电子设备这样的“双高”特点。大量电力电子设备的接入,降低了系统整体的转动惯量,恶化了系统的稳定性[1-3]。尤其当100%电力电子设备独立组网时,系统的抗扰能力更弱,稳定性更差。
纯电力电子设备组网的新能源发电系统中,根据同步方式的不同,换流器的控制类型可以分为跟网型控制(Grid Following Control)和构网型控制(Grid Forming Control)[4]。跟网型换流器通过锁相保持与主网的同步,无法直接控制电压和频率,应用于弱电网情况下会降低系统的稳定性。而构网型换流器在连接分布式电源后可被看作耦合电抗后的可控电压源,能够主动建立系统频率和电压,并对系统提供惯性支持,其对电网的支撑及独立控制效果更好[5,6]。已有研究证实了构网型换流器可随其渗透率的提高而实现更好的响应特性,动态性能优于跟网型控制[7,8]。目前,常见的构网型控制主要有虚拟同步发电机(Virtual Synchronous Generator, VSG)控制、下垂控制、匹配控制[9-11]等。其中,VSG控制模拟同步发电机的特性,对电网具有较强的适应性和鲁棒性[12,13],下垂控制可实现无通信功率分配。两者共同组网具有较强的互补性,VSG控制单元模拟传统发电机,提供频率的强支撑,下垂控制单元协调各端功率输出,实现系统的功率平衡。但是,构网型换流器因其电压源特性对外部干扰非常敏感,其过电流抑制方法需特别关注[14-16]。传统同步发电机可短暂承受高达7倍的额定电流,而电力电子换流器只能承受1.2~1.4倍的过电流[17]。因此,当多端构网型换流器独立组网时,限制系统过电流成为一个亟待解决的问题。
针对换流器的限流策略,目前大多是基于跟网型控制采取的限流措施。文献[18]中采用比例控制的电压外环,通过电压控制器中的前馈电流项和椭圆规则来限制电流大小。文献[19]提出了增设电压限制器的控制方法,主动控制电压以获取合适的电流值,该方法对三相短路效果明显,但对于不对称故障来说存在局限性。文献[20]通过虚拟阻抗与滤波电容并联来避免限压,进而限制故障电流。文献[21]提出了一种阈值虚拟阻抗限流方案,虽保证了系统的小信号稳定性,但大扰动下的稳定性需深入研究。文献[5]通过电流限制器直接控制电流大小,文献[22]分析了系统接地故障情况下上述方法带来的暂态不稳定现象。为改善这种不稳定现象,有学者对虚拟阻抗限流和直接限流方案的优势与局限性进行分析,提出了一种混合限流策略,但如果故障持续时间长,不稳定风险仍然存在[23]。目前,针对跟网型换流器过流抑制方法的研究主要集中在短路故障,且故障持续时间较短。而对由构网型换流器组成的100%电力电子系统中发生大干扰扰动且持续时间较长的情况,仅限制单端换流器的输出电流容易引起系统电压崩溃[24]。因此,有必要对构网型换流器间的协同限流控制方法进行研究。针对多端同类型换流器协同配合开展电压调节、频率控制的研究已有很多,但对基于不同控制类型的构网型换流器组网的100%电力电子系统,多个换流器间如何协同限流的策略有待深入研究。
针对上述问题,本文提出一种基于不同控制类型的构网型换流器间协同限流控制方法,以解决不同构网型换流器组网时由于扰动造成的输出过电流问题。首先,本文构建了100%电力电子设备组网典型系统,该系统中包含两种不同控制类型的构网型换流器。其次,针对单端构网型换流器设计了一种基于电流饱和算法(Current Saturation Algorithm, CSA)的电流限制方法,以限制端口换流器的暂态过电流。在此基础上,提出了一种构网型换流器间协同限流控制方法,可实现限流控制与正常工作模式间的平滑切换。然后,对100%电力电子设备组网进行小信号建模,利用根轨迹分析所提策略中的控制参数对系统稳定性的影响。最后,通过控制器级硬件在环实验对本文所提控制策略的有效性进行验证。
1 拓扑结构和控制策略
1.1 系统拓扑
传统交流电网可以通过大型旋转同步电机对系统的电压和频率进行控制和调节,由于旋转电机惯性和阻尼的存在,使得故障发生时电压和频率的变化更有利于电力系统的稳定。而随着新能源大规模应用,100%电力电子设备组网系统逐渐增多,由于缺少同步发电机,系统惯性较低,稳定性能较差,电力电子设备组网后的安全稳定运行极为重要。
依据典型的三机九节点测试系统,构建基于构网型控制的电力电子组网系统如图1所示。该系统包含三个大功率聚合型变流器,其控制类型为构网型典型控制,主要包括VSG控制和下垂控制。在此系统中,VSG控制单元是替换发电机的较好选择,而系统中的下垂控制单元在传统电网中也比较常见,此时系统有功功率控制仍以频率为主要的控制对象,在频率响应特性上与传统电力系统差异不大,两者组网具有一定的互补性和典型性。

图1 100%电力电子三端九节点测试系统Fig. 1 Three terminal nine node test system with 100% power electronics
1.2 基于VSG控制的构网型换流器
VSG控制策略通常应用于含储能元件的分布式电源侧并网换流器,其基本思想是通过模拟同步发电机的输出外特性来提高电力系统的稳定性。本文给出VSG控制的典型结构如图2所示,其主要由储能单元、逆变装置以及VSG控制器组成。图中Udc为源端等效直流电压,eabc为换流器端口电压,uabc为换流器网侧电压,iL为滤波电感上的电流,iabc为并网电流,P0为有功功率给定值,ω0为电网角频率参考值,Uset为交流电压参考值,Gu(s),Gi(s)分别为电压、电流控制环的传递函数,L为滤波电感,C为滤波电容,R为换流器等效电阻。
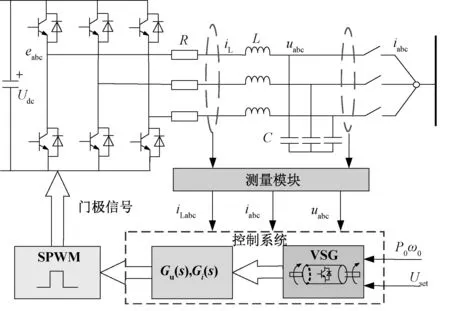
图2 典型VSG控制结构图Fig. 2 Structure diagram of typical VSG control
1.2.1 频率无偏差的有功-频率控制
VSG控制器的机械部分主要模拟了同步发电机转子运动方程的阻尼和惯量特性,其实现方式如式(1)所示:
(1)
式中:J为VSG的转动惯量;ω表示换流器端口角频率;Dp为阻尼系数;Pm、Pe为VSG模拟机械功率和电磁功率;θ为VSG模拟的转子电角度。
传统有功-频率控制部分模拟同步发电机调频器,通常采用下垂控制形式,为频率的有差调节。由于纯电力电子组网系统对频率变化较为敏感,要求VSG控制单元实现对电网频率的无偏差调节。本文在传统控制基础上增加一个积分环节,如式(2)所示,积分调节可消除系统频率的稳态误差。相当于改变虚拟同步发电机的静态频率特性,模拟发电机的二次调频环节,控制框图如图3所示。

(2)
式中:mω为有功-频率控制的下垂系数;mi为调频环节积分系数;t和τ为时间变量;ω(τ)表示τ时对应的角速度。
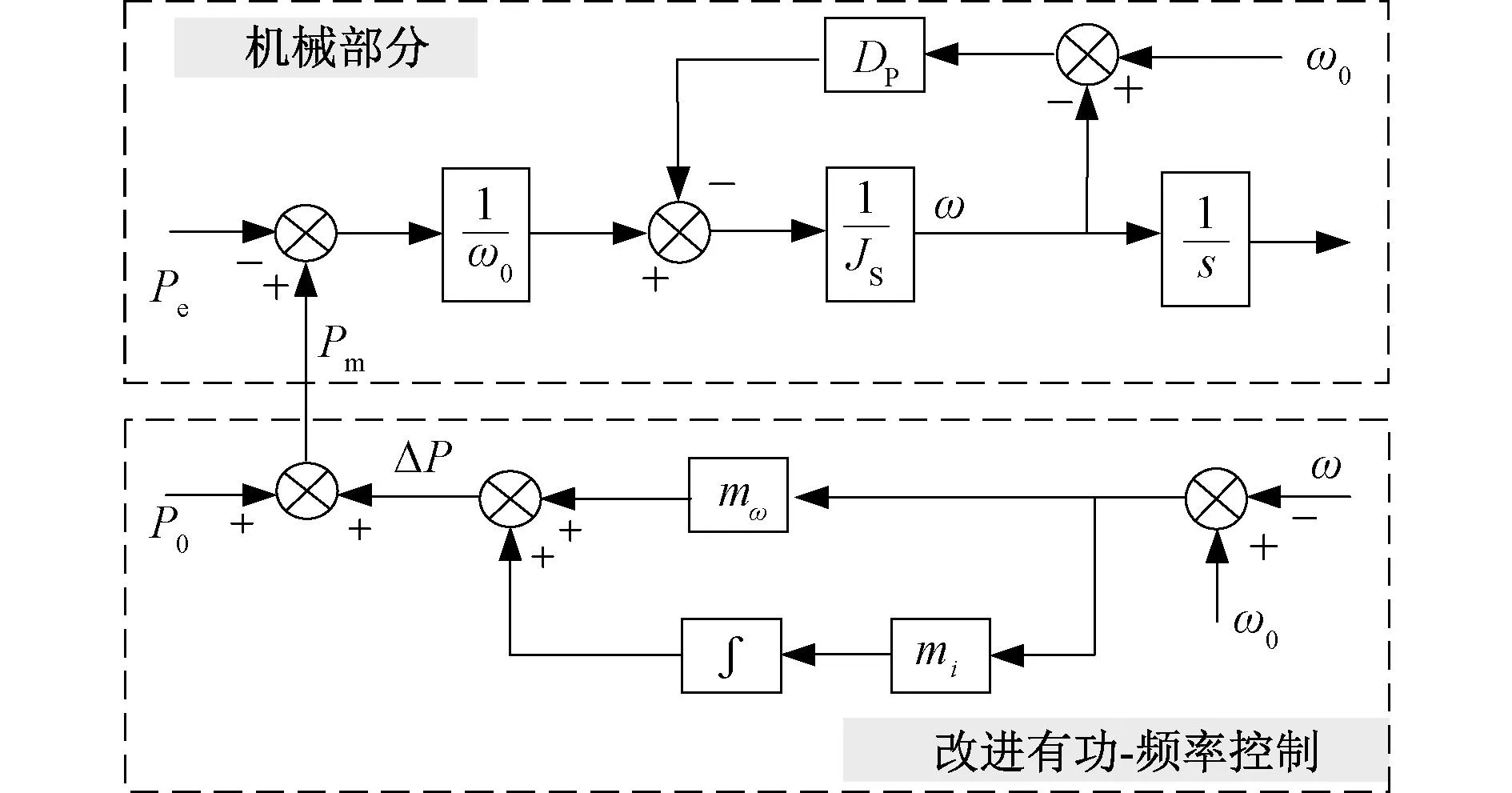
图3 频率无偏差的有功-频率控制框图Fig. 3 Block diagram of VSG active power-frequency control without frequency deviation
1.2.2 电压自动调节控制
为更精准的模拟同步发电机的运行机制,除了在频率控制环节加入发电机的转子运动方程外,还在电压控制环节加入模拟了同步发电机的机电耦合特性环节。充分考虑了同步发电机的机电与电磁特性,根据发电机的物理与数学模型可得:
(3)
式中:Mf为模拟的发电机励磁与定子绕组间的互感电动势;if为模拟的发电机励磁电流;e为模拟的定子感应电动势。
本文将电压控制环节设计为电压自动调节控制,通过PI控制器控制输出电压与参考值的误差,得到所需要的励磁电流if值,控制框图如图4所示。
(4)
式中:uodq为测量电压;uodq(τ)表示τ时的测量电压;k1和k2分别为自动调压控制环节的比例和积分系数。
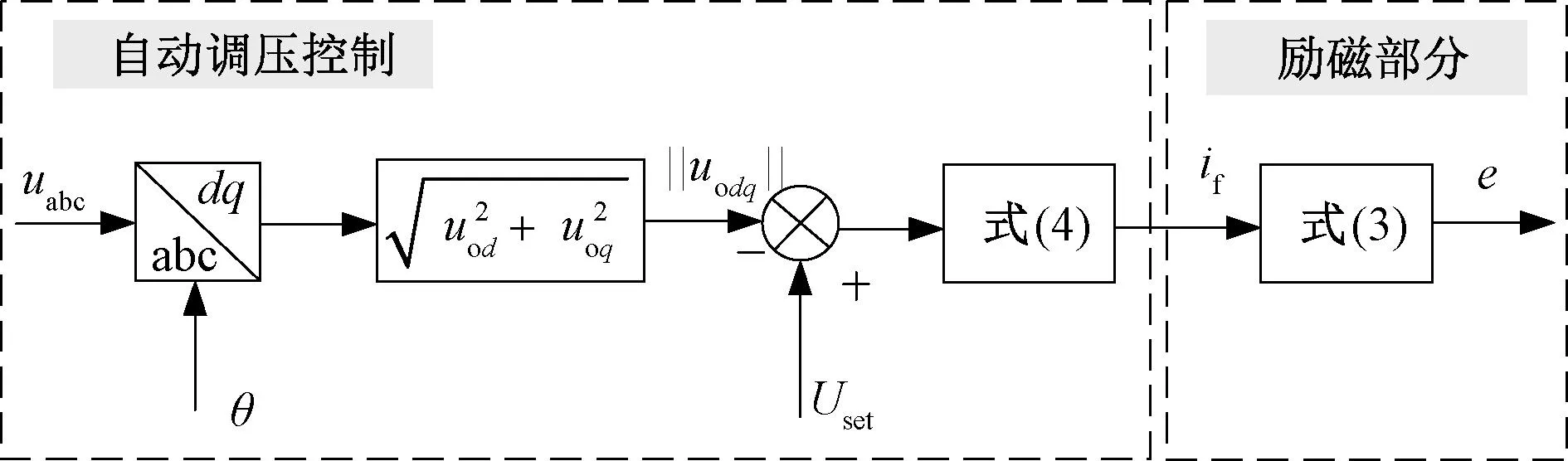
图4 自动调压控制器Fig. 4 Block diagram of automatic voltage regulating controller
1.3 基于下垂控制的构网型换流器
下垂控制通过模拟发电机机组的功频特性使分布式电源共同参与维持系统频率和电压的稳定。本系统中基于下垂控制的换流器为构网型,频率及电压支撑能力必不可少。换流器的电压控制环节采用同VSG控制单元相同的自动调压控制,其有功-频率环节的核心控制方程如式(5)所示,控制框图如图5所示。
(5)
式中:mP为下垂系数,P0为有功功率给定值;P为有功功率测量值。

图5 Droop控制有功-频率控制框图Fig. 5 Block diagram of Droop active power-frequency control
1.4 VSG控制与下垂控制的比较分析
VSG控制与下垂控制具有相似的有功频率下垂稳态特性,两种方案可通过参数设置使输出频率具有相同的响应特性,区别在于VSG控制通过同步发电机转子运动方程模拟了频率的阻尼和惯量特性,其控制参数与发电机参数一一对应,具有更明确的物理意义。而下垂控制可以通过下垂特性实现各分布式电源间的无通信负荷功率分配。本系统中VSG和下垂控制单元之间的功率分配原理同上述无通信负荷功率分配原理类似,通过下垂系数进行功率分配,由于下垂控制是有差的,而用来消除频率误差的功率由VSG单元额外承担。以上两种控制类型的构网型换流器混合组网,实现优势互补,增加了100%电力电子设备组网系统的稳定性。
2 构网型换流器的限流控制
2.1 单端构网型换流器的暂态限流控制策
为解决大负荷扰动后单端构网型换流器的暂态过电流问题,本文在电压电流双闭环控制设计中引入电流饱和算法(Current Saturation Algorithm, CSA)的概念。绘制VSG单元的控制框图如图6所示,图中kpwm为调制波的比例系数,iLref、iL分为电感电流参考值和实际值,iC为电容电流。
CSA控制器的限流原理如下:
(6)
(7)

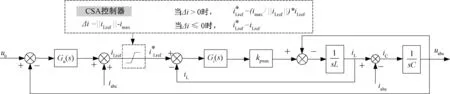
图6 附加CSA控制的VSG控制框图Fig. 6 Block diagram of VSG control with CSA
根据图6的控制框图可知换流器的输出电流的数学表达式如下
iabc=G1(s)iLref-G2(s)uabc
(8)
(9)
式中:kp、ki为电流内环的比例系数和积分系数。
代入表1的相关参数,可绘制式(9)的伯德图如图7所示。
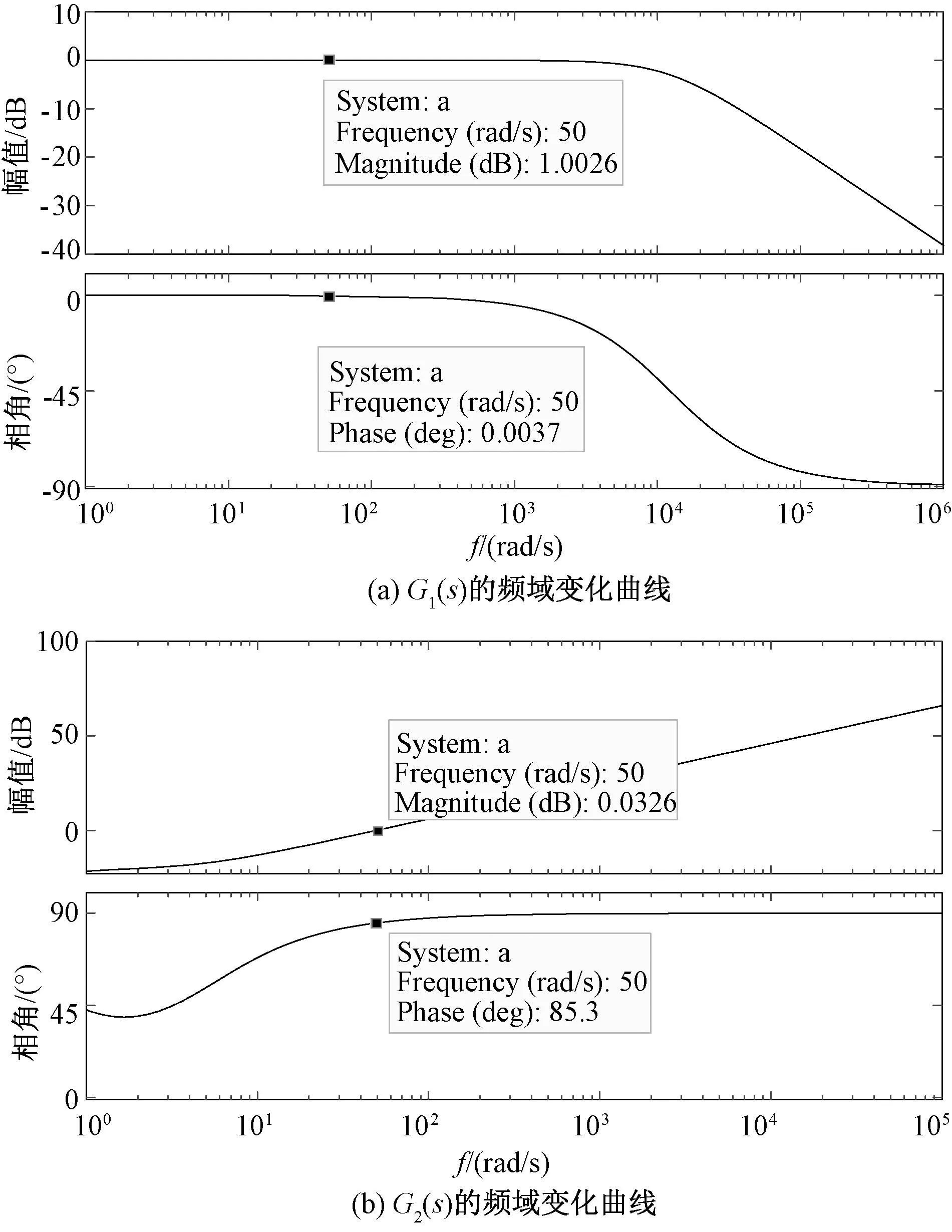
图7 G1(s)、G2(s)频域变化曲线的影响Fig. 7 Frequency domain variation curve of G1(s) and G2(s)
由图7可知,G1(s)的幅值为1且相角为0°,G2(s)的幅值近似为0,系统的输出电流iabc最大可能追踪电流内环的参考值iLref。所以CSA控制器通过将电流内环的输入参考值iLref限制在规定范围内,实现将换流器的输出电流iabc限制在规定范围内。
2.2 多端口换流器协同限流控制策略
文中所研究的电力电子组网系统包含一个VSG控制单元,两个下垂控制单元。由于下垂单元的频率调节是有差的,所以系统频率的二次调节是由VSG控制的构网型换流器实现的。当系统中出现较大扰动时,频率波动较大,VSG控制单元将承担主要的有功负荷波动量。基于VSG控制的构网型换流器在给电网提供频率支撑的同时,会存在明显的过流问题。单纯限制单端换流器的输出电流,难以保证系统的稳定性。为保证组网系统的长期稳定运行,需要协调多端口换流器共同参与系统的功率分配,以实现限制电流目的。
当系统中出现大扰动后,考虑VSG的二次调频控制,其稳定运行时的功率分配为
(10)
式中:ΔP为主要的有功负荷波动量;Pi0为系统原始稳态时的功率参考值;Pi为扰动发生后的功率参考值;其中i=1、2、3,分别代表VSG控制单元,下垂控制单元1和下垂控制单元2。
本文根据VSG控制换流器的过流程度,自适应修改下垂控制换流器的有功功率设定值,基于电流变化量的功率修正控制如式(11)所示。
(11)
式中:ΔPref为有功功率设定值的修正量;iLdq1为基于VSG控制的构网型换流器的dq轴电感电流值;k3、k4为电流变化量的比例系数和积分系数。
考虑协同限流控制的系统功率分配如式(12),以下垂控制单元1为例,其控制框图如图8所示。
(12)

图8 修正有功功率设定点后的有功-频率控制框图Fig. 8 Block diagram of active power-frequency control after correcting active power set point
2.3 限流控制与正常工作模式间的平滑切换
实际电网中负荷扰动是波动的,可随时出现或消失。本文所提基于功率自适应修正的协同控制策略中包含积分环节,当系统负荷扰动消失后,由于积分环节作用ΔPref将一直保留,影响微电网中各个换流器在扰动消失后的正常输出。为保证系统可以在负荷扰动复杂变化的情况下安全稳定运行,需要在扰动清除后置零ΔPref以保证系统的正常运行,即需要实现限流控制与正常工作模式间的平滑切换。
引入符号函数sgn(x),如式(13)所示,通过判断换流器的输出电流值与电流最大允许值的差值,选择合适的控制策略。
n=sgn(‖iLdq1‖-imax)=
(13)
式中:n为限流控制与正常工作间的切换信号。
所提协同限流控制及平滑切换策略的控制框图如图9所示,通过VSG控制换流器的电感电流与电流最大允许值计算n值。当n>0时,系统进入限流模式,根据VSG的过流程度,由式(12)计算出合适ΔPref值,修改下垂单元的功率参考值,通过降低VSG的输出功率来降低其输出电流值;扰动清除后,此时n≤0,为清除积分器存储的ΔPref值,将功率修正值置零,此时为正常工作模式,三端换流器的稳态负荷分配回到正常状态。
3 小信号建模与稳定性分析
为分析所提协调限流控制中相关参数对系统稳定性的影响,对图1所示的100%电力电子组网系统进行小信号建模,建立多端系统的状态空间表达式,通过根轨迹法分析协调控制中各参数变化对系统稳定性的影响。
3.1 统一坐标系
建立统一的坐标系如图10所示,图中DQ轴为基本参考系,dq轴为第i个换流器的坐标系。

图10 基本参考系Fig. 10 Basic reference system
如图所示,第i个换流器单元与基本参考系间的相角差δi为
(14)
式中:ωi为换流器单元i的输出角频率;δi0为换流器i与基参考系之间角度差的稳态值;ωcom为参考系的角频率。
根据图可知,dq轴与基本参考系DQ轴之间的转换公式如下:
(15)
式中:f代表换流器在不同坐标系下的相关参数。
3.2 VSG控制单元小信号模型
通过VSG单元输出电压和电流值的dq轴分量计算其产生的瞬时功率,然后经过一阶滤波器得出平均有功功率
(16)
式中:ωf为滤波器的角速度;uod、uoq为输出电压值的dq轴分量;iod、ioq为换流器单元输出电流值得dq轴分量。
对式(16)进行线性化,得到P的小信号表达式:
(17)
式中:Uod、Uoq、Iod、Ioq为系统稳态值。
根据图2绘制换流器端口滤波线路的拓扑图如图11所示,图中RT、LT为考虑变压器情况下换流器与并网点(PCC点)之间的等效电阻和电感。
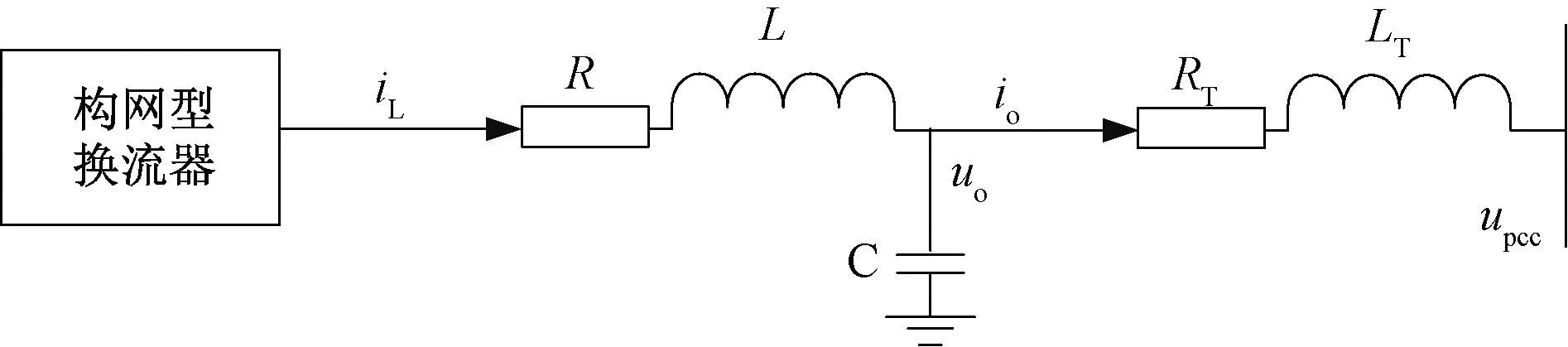
图11 滤波线路的拓扑图Fig. 11 Topology of filter circuit
根据图11,写出线路的数学表达式:
(18)
式中:iLd,iLq为电感电流dq轴分量;upccd、upccq分别为PCC点电压的dq轴分量。
对VSG控制单元的相关公式进行线性化,可得到公共坐标系下的VSG单元的状态空间表达式:
(19)

(20)
式中:Δφ1为二次调频环节的状态变量;Δx0d1为自动电压控制环节的状态变量;矩阵参数见附录。
3.3 Droop控制单元小信号模型
对增加协同限流控制后的Droop单元进行小信号建模,参照VSG的小信号模型可得到在公共坐标系下的Droop单元的状态空间表达式如下:
(21)
(22)
式中:Δxci为限流控制环节的状态变量,i取2、3;相关矩阵参数见附录。
3.4 100%电力电子组网系统的小信号模型
选取VSG单元的dq坐标系为网络的基本坐标DQ,即ωcom=ω1,整合三个构网型控制单元,可知整个网络系统的状态变量为△xs如式(23)所示:
(23)
组网系统的小信号模型如下:
(24)
式中:ΔupccDQ为基本参考系下的PCC点电压;矩阵参数见附录。
3.5 系统稳定性分析
在电力电子设备组网系统模型建立的基础上,对本文所提的协同限流策略中的控制参数进行稳定性分析,系统控制参数如表1所示。

表1 系统参数
由式(24)可知系统有32个特征根,选取相关参数的主导特征根并对其根轨迹进行分析。选定k3变化范围为100~10 000时,主导特征根的根轨迹如图12(a)所示,λ1和λ2为一对共轭特征根,随着k3的增大,特征根先远离虚轴然后快速靠近虚轴,系统的阻尼比从不变到逐渐减小。可知,系统的稳定性随着k3的增大而增加,当k3大于2 000时,系统稳定性开始下降,振荡程度逐渐加大。选定k4变化范围为1 000~20 000时,其跟轨迹如图12(b)所示,λ3和λ4为一对共轭特征根,而λ5是一个负实根。随着k4的增大,特征根λ3和λ4开始远离实轴和虚轴,系统的阻尼比逐渐减小,导致系统的振荡程度加大。同时,λ5逐渐靠近虚轴,系统稳定性明显降低。
4 仿真分析与硬件在环测试
为了验证本文所提控制策略的有效性,通过RT-LAB实时仿真系统进行实验验证。硬件在环测试系统如图13所示,此系统包括数字信号处理器(DSP)、录波仪(DL850)、上位机等实验装置。将本文所提控制策略部署在实际的DSP控制器中,所搭建的电力电子组网系统模型放置在RT-LAB中,DSP控制器输出的调制波(SPWM)经过光电隔离模块与RT-LAB的调制波输入端口相连,通过录波仪对实验波形进行测量记录。
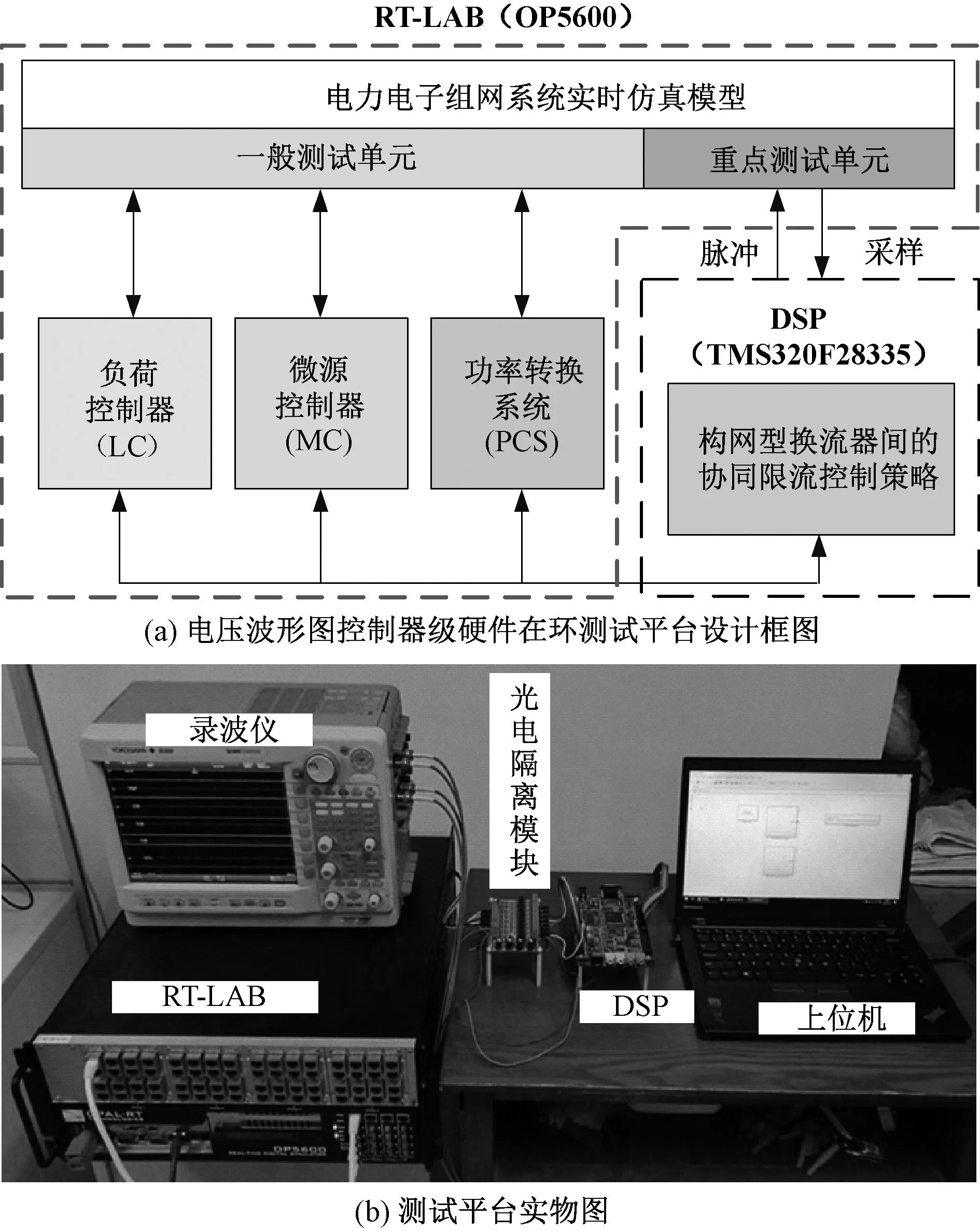
图13 硬件在环测试系统Fig. 13 Hardware in loop test system
4.1 构网型换流器的控制效果
以VSG控制单元为例,为验证其频率无偏差调节效果,与传统方法进行比较。设置10 s时,负荷突增0.9 pu,由图14可清晰看出频率无偏差控制策略可以将系统的频率稳定在50 Hz,并在系统出现大扰动情况下,通过快速调节换流器的有功功率输出调节系统频率,实现了系统频率的无差调节。
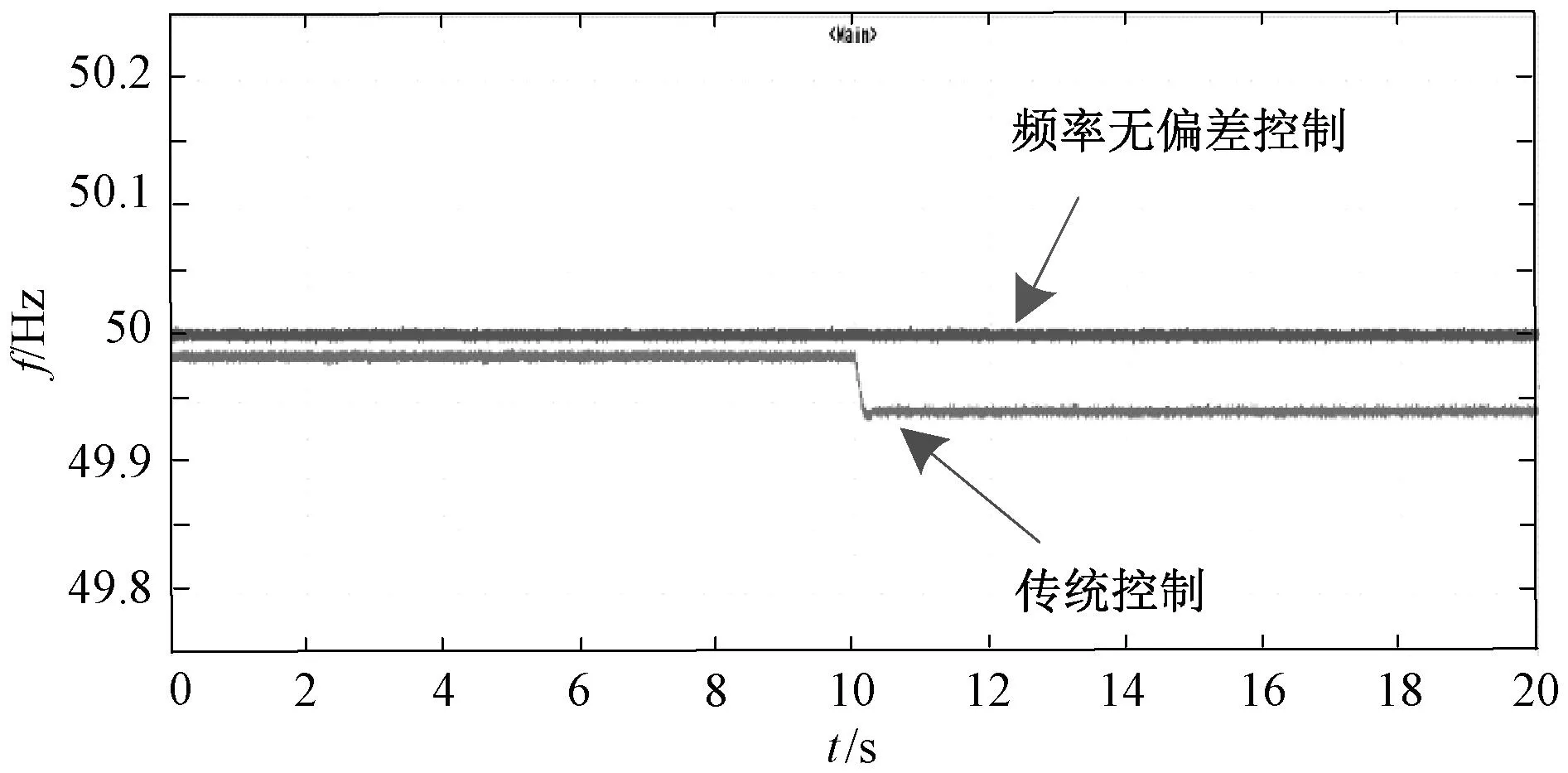
图14 频率无偏差控制与传统控制实验波形图Fig. 14 Frequency waveform of frequency deviation free control and traditional control
对采用自动调压控制的VSG单元进行实验仿真,为更好反应控制策略的有效性,对于交流电压(后文的交流电流)采用其方均根值表示,在10 s时负荷突增,15 s时负荷突减,从图15可知负荷扰动情况下,构网型换流器可以稳定系统电压。

图15 VSG端口电压变化曲线Fig. 15 Voltage waveform of VSG control converter
4.2 单端构网型换流器的限流控制效果
设置仿真工况,在5 s时,系统负荷突增0.25 pu,对VSG控制构网型换流器是否采用CSA控制器的情况进行仿真,仿真波形图如图16所示。可知本文所设计的基于电流饱和算法的电流限制方法有效的将单端构网型换流器的输出电流限制在最大允许电流。

图16 换流器采用CSA控制器前后的电流波形图Fig. 16 Current waveform before and after converter adopts CSA controller
4.3 多端口换流器协同限流控制效果
当系统中未采用任何限流控制策略时,设置仿真工况,在t=5 s时,负荷突增ΔP=0.5 pu,对文中的三端九节点系统进行仿真分析。
根据上文可知,VSG单元的二次调频可以确保交流微电网频率保持不变,此时两个下垂控制的构网型换流器相输出功率几乎不变,所以系统的负荷扰动分量由VSG控制的构网型换流器单独承担,承担过大的负荷分量将会导致该换流器出现过流问题。从图17可明显看出,基于VSG控制的构网型换流器的输出电流达到了1.6,远超过额定电流的1.2倍,换流器的安全性受到威胁。
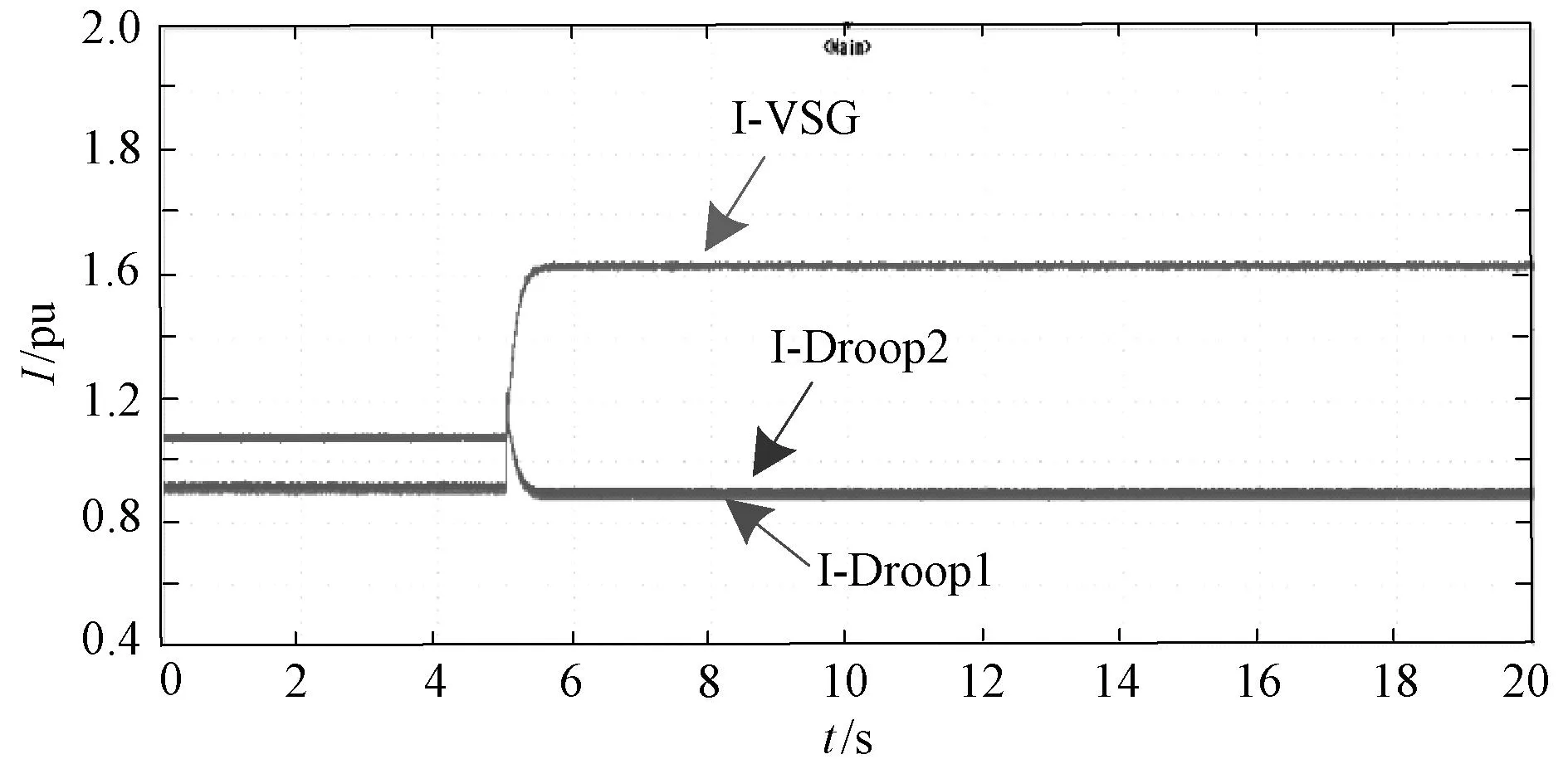
图17 未施加协同控制策略时各变流器的电流波形Fig. 17 Current waveform of each converter without collaborative control strategy
实际仿真中三端构网型换流器均增加CSA控制,对系统进行仿真,结果波形图18所示。组网运行过程中,大干扰扰动发生后,VSG控制的构网型换流器进入限流模式后,由于CSA的强制限流,VSG单元输出无功功率不满足负荷所需,系统的电压和电流开始下降。电压下降到一定程度后,导致自动调压控制器的PI控制器饱和,电压调节失效,电压加速下降,而电流开始增加最后被一直限制在最大允许电流值。

图18 仅采用CSA时各变流器的电压电流波形Fig. 18 Current and Voltage waveforms of each converter only with CSA
图18(a)可知扰动发生初期系统频率发生变化,下垂控制单元增加系统输出,下垂单元稳定1 s左右,由于VSG的电压加速下降,其输出功率开始下降。此时下垂控制单元的输出功率增加,直到输出电流达到限定值后,PI控制器饱和,电压调节失效,下垂单元输出电压开始下降,三端换流器电流均进入限流模式后,将迫使变流器在电流过剩期间作为恒流源工作,电压调节控制均失效,其功率输出变得不可控,为恒定电流和换流器输出端电压的乘积。这破坏了功率同步所需的功率平衡,变换器失去同步,因此系统崩溃。
为有效解决电力电子组网系统中的过流问题,避免系统电压崩溃,在CSA控制下,增加不同类型构网型换流器间的协同限流控制策略。根据VSG控制换流器的电流偏差量,修改下垂控制单元的功率设定值,降低VSG控制单元的功率输出,进而限制电流,仿真波形图如图19所示。
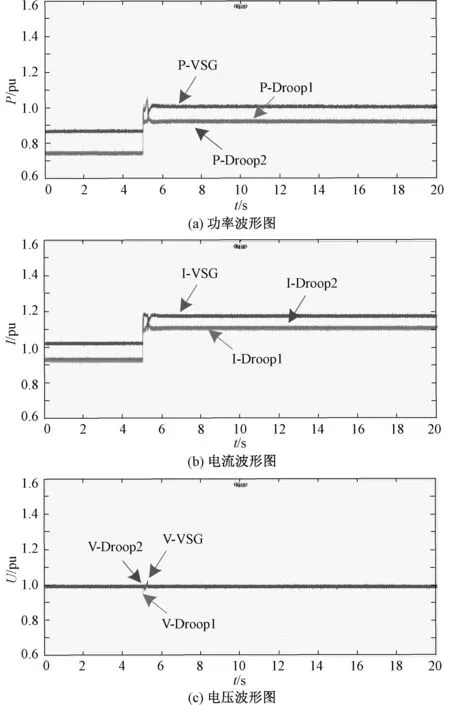
图19 增加协同控制后各换流器的仿真波形图Fig. 19 Simulation waveform diagram of converters with CSA and collaborative control strategy
图19(a)可以看出,采用协同限流控制后,系统重新分配了各单元分担的负荷分量。由图19(b)可知,各换流器的输出电流值均被限制在规定电流范围,而且CSA控制器有效限制了暂态过电流。图19(c)和图18(b)对比可知,采用协调控制的组网系统在扰动发生后母线电压稳定。
4.4 限流控制与正常工作模式的平滑切换效果
为了验证限流控制与正常工作模式平滑切换方法的有效性,增加几种负荷变化场景:5 s时,突增负荷0.35 pu;9 s时,负荷骤减0.35 pu;13 s时,突增负荷0.6 pu;17 s时,负荷骤减0.6 pu。
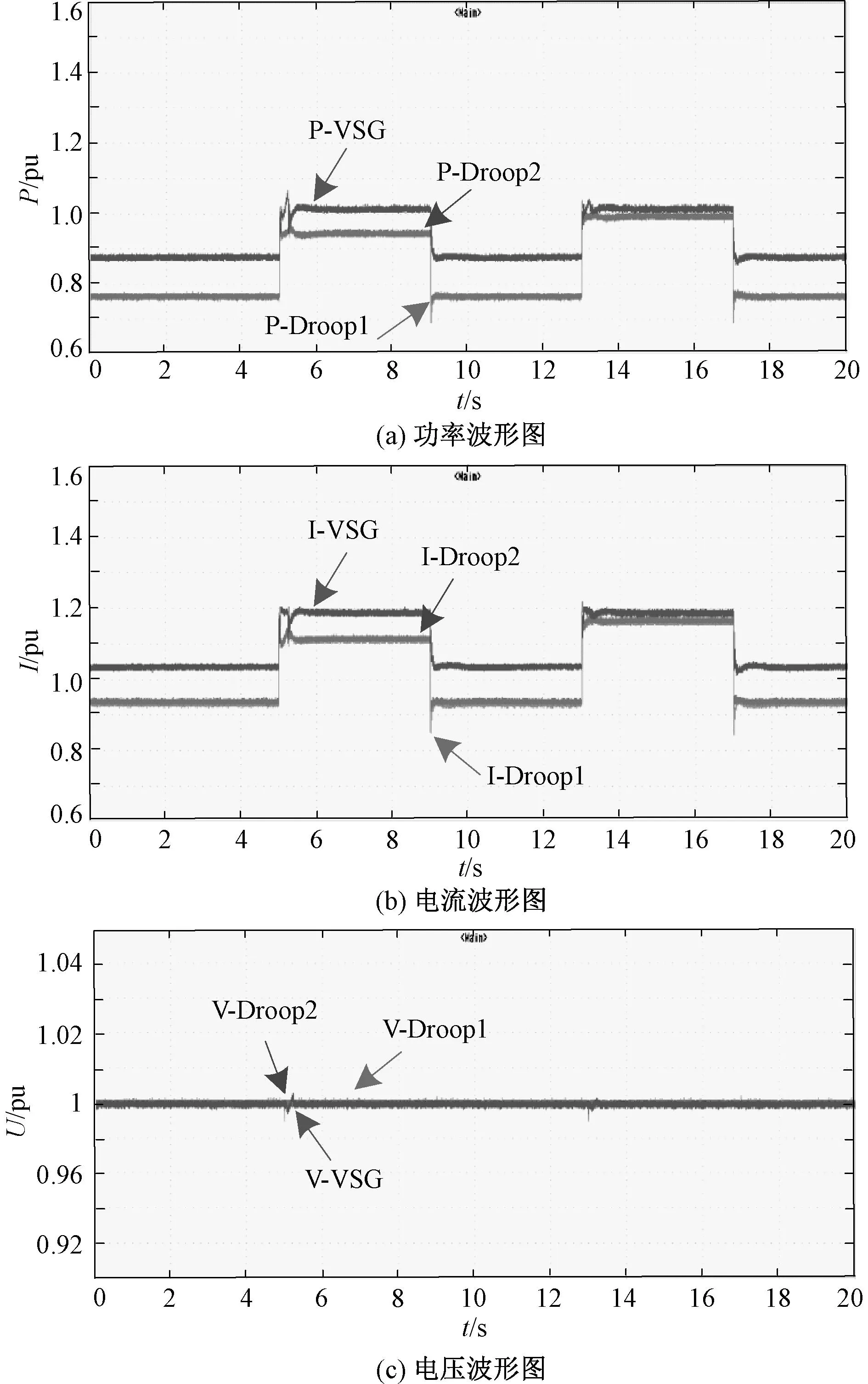
图20 复杂工况下增加电流限制后换流器的仿真波形图Fig. 20 Waveform of converters with CSA and collaborative control strategy under complex working conditions
图20给出在复杂工况下构网型换流器的输出波形,从图20(b)可以看出负荷突增后,构网型换流器的输出电流均被限制在最大允许电流,满足其长期稳定运行的要求,在突增负荷消失后,系统的控制策略由协同限流模式切换到正常工作模式,系统恢复原始状态,正常平稳运行。
5 结 论
本文构建了包含两种控制类型的构网型换流器的100%电力电子组网系统,并通过RT-LAB实时仿真平台对本文所提控制策略进行验证。通过理论分析及测试结果得到如下结论:
(1)针对单端构网型换流器在大负荷扰动过后出现的过电流现象,本文设计了一种基于电流饱和算法的电流限制方法,有效限制单端换流器的暂态过电流。
(2)本文提出了一种基于不同控制类型的构网型换流器间协同限流控制方法,解决了大扰动情况下换流器输出电流过大的问题。同时,所提方法可实现限流控制与正常工作模式间的平滑切换,具有较好的实用性。
(3)对100%电力电子组网系统进行小信号建模,通过根轨迹分析了所提协同限流控制中控制参数对系统稳定性的影响,为选择系统控制参数提供了理论基础。
