基于贝叶斯优化LightGBM算法的主动式搜索时间调整方法
2024-04-17马天祥
刘 青, 鲁 成, 马天祥, 段 昕
(1.新能源电力系统国家重点实验室(华北电力大学) ,河北 保定 071003;2.国网河北省电力有限公司电力科学研究院,河北 石家庄 050021)
0 引 言
“碳达峰”目标的提出加速了我国配网中分布式新能源应用比例的提高,过去能源单向流动的形式变成了可变双向流动,配网中拓扑关系日益复杂。新投入的城市配网更多地采用环网设计以提高供电可靠性指标,雄安地区、广州等地更是采用了“双花瓣”结构。复杂的多端多电源网络使得现有的配网三段式过流保护配置方案难以继续使用[1-3],节点与连接关系大大增加,因此差动保护与馈线自动化技术被引入配网保护中。然而传统差动保护采用的光纤介质使用维护成本高,不适合配网中推广,十分限制配网继电保护业务的开展与技术提升。
为此,大量专家学者基于我国5G通信研究进程[4,5],针对配网保护业务5G化进行了应用研究。文献[6]针对5G通信应用于馈线自动化的方案进行了详细的论述,并搭建实验平台实现了终端延迟、动作全流程时间的测试。文献[7]从差动保护对通信效果的要求出发,基于国内首个5G SA/NSA双模基站组网的电力系统业务平台,测试了外场环境下终端之间延迟与抖动情况,并提出了延迟抖动优化措施。文献[8]提出了不依赖外部时钟的基于故障时刻5G数据同步方法,在10 kV线路上实现了基于5G通信的配网差动保护功能。但是在实际应用时,终端常常因通信延迟过大影响了保护动作可靠性,因此就有思路提出通过预测延迟,以主动适应延迟的变化。
目前电网中的延迟预测业务尚是空白,但负荷业务预测十分常见,其中短期负荷预测针对的是未来数小时或是数天的负荷曲线,这一需求与延迟预测的特征十分接近。现阶段对于短期预测的方法主要通过统计学方法与机器学习,前者原理简单,但是难以处理体积庞大的数据集;后者基于机器学习算法,包括支持向量机、随机森林算法与遗传网络[9-11]等,挖掘数据间规律能力较强。但是这类算法对于时间序列的处理不够理想,难以从时间关联中提取有效信息,于是长短期记忆网络(Long-short Term Memory, LSTM)为代表的神经网络就克服了这一问题,充分挖掘时序信息里的深层关系,但其对于非连续特征的处理效果又是一大劣势。为了克服单一模型的不足之处,诸多集成学习方式应运而生。文献[12]提出一种结合GRU与LSTM的模型,利用GRU单元预处理负荷历史信息,再结合其他特征输入LSTM中训练。文献[13]引入注意力机制,改进了传统CNN-LSTM网络,设计了分季节进行的短期负荷预测。
针对短期5G配电终端延迟预测问题,本文提出一种基于贝叶斯优化LightGBM算法的主动式搜索时间调整方法。模型以LightGBM算法为核心,将历史延迟数据与日期、时间、温度等因素作为输入,训练过程中引入贝叶斯优化方法寻找最优参数,最后通过计算最优权重,结合上一时刻的延迟实测值动态调整预测值。实验证明,本文提出的方法预测精度较其他方法具有突出优势,可以很大程度上解决因延迟波动导致保护装置闭锁的问题。
1 5G配电终端延迟预测
1.1 配电终端延迟要求
智能电网的强大离不开通信技术的支持,涵盖多样化的通信服务需求,5G网络在电网为代表的垂直行业的应用场景下迸发出新的发展火花[14],而其中差动保护业务被认为是5G低延时、高精度授时的原型业务。图1为基于5G通信的馈线自动化网络架构示意图。规定中要求[15],考虑设备热稳定性因素,保护装置需要在0.1 s内完成报文交互,故障分析,跳闸命令下达,断路器物理跳闸结束这一系列动作。

图1 基于5G通信的馈线自动化网络架构示意图Fig.1 Network architecture of 5G-based FA
如图2所示,扣除保护装置运算、命令触发、断路器动作的时间,预留给报文传输的时间小于20 ms。同时规定了极高的可靠性需求,尽量杜绝误码、断连等引起保护装置拒动、误动的现象。由于无线路由路径差异,排队等待发送或是保护两侧装置性能差异引起的延迟抖动,也会直接给保护装置的处理加入不平衡电流,增加了误动的可能性。
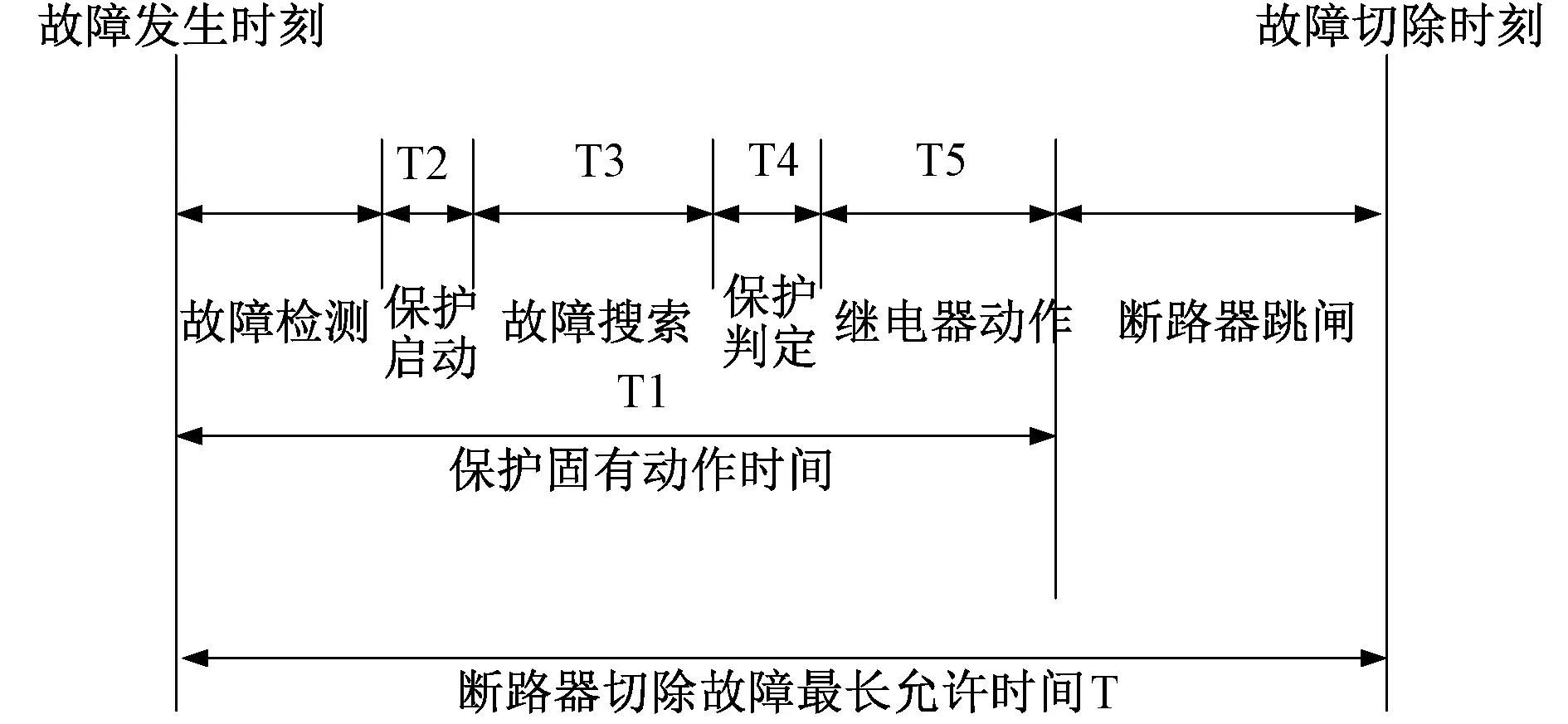
图2 故障切除时序图Fig.2 Fault removal sequence diagram
而5G通信馈线自动化技术,由于不采用差动保护原理,对于通信的要求就没有那样苛刻。通常来说,规定要求10 kV变电站出线开关可以在最多0.3 s内完成动作[16-18],而断路器分闸时间不超70 ms。保护终端在检测到本地故障出现后,会向对侧终端发送故障信号,同时启动故障搜索等待时间TW。在故障等待倒计时结束后,会将本地与周围开关交换的信息结合起来判断故障情况。同时TW可以兼顾保护装置与相邻装置连接关系的确认信号,如果收不到对端信号,则说明故障为区外故障,保护闭锁。实际运行中,延迟与抖动常常超过固定的TW值,导致装置偶发性闭锁,若此时区域内发生故障,就必定会导致拒动现象,处理不及时就会在配网内引起大面积蔓延,危及生产生活。
1.2 延迟预测原理分析
延迟(delay或latency)又叫时延或延时[19],包括几个部分:发送延迟,传播延迟,处理延迟,排队延迟。简要来说,无论是主机或路由器完整发送一段数据帧,基站发送无线信号到终端的空口过程,芯片处理数据,还是排队等待发送,每一个环节都会增加终端之间互联互通消耗的时间。
抖动指的是分组延迟的变化程度,基本上是不可预测的[7],影响因素众多,但是根据分析结合历史数据可以认为,延迟却是可以进行预测的。由终端发送信号到达另一个终端通常要经过“终端-空口-基站-光纤-承载网-对侧基站-空口-对策终端”的流程,基站及其之间使用光纤介质,与有线网络共用一个架构,设计承载量巨大,能够满足大量用户的连接。因此延迟的主要不稳定环节来自基站到终端之间的空口因素,根据研究,过高/低的温度、降水、雾霾、建筑物遮挡以及红外反光玻璃穿透等物理因素[20-24]都有可能影响5G频段电磁波的传播性能,另外高温极易影响基站、收发机、天线的性能。
结合延迟记录可以发现,日延迟曲线都是呈现一定规律的:从形式上看,波动较大,不够圆滑;从时间上来说,基本随着居民日生产生活强度发生变化,基站连接数也会变化,延迟也就随着波动。而在夜间连接数大幅减少时,基站会进入低功耗模式,此时发射信号减弱,也会一定程度上导致延迟增加。本文设计配合特征变量,对延迟进行预测,实现搜索等待时间TW的动态修改:当预测到下一采样时刻延迟会超过当前TW时,在不超过总动作时间0.3 s的规定下,主动调整TW大小,避免装置闭锁现象。
2 基于LightGBM模型的延迟预测方法
2.1 LightGBM模型
LightGBM是以梯度提升决策树(Gradient Boosting Decision Tree,GBDT)为基础的集成学习算法,它改进了GBDT的缺点,从而能更适合工业应用。在此之前,基于决策树模型(弱分类器)迭代训练的GBDT框架在分类、预测以及数据挖掘等场景得到了广泛应用。为了解决GBDT在海量数据遇到的问题,LightGBM进行了几项优化措施,包括:基于直方图(Histogram)的决策树算法、带有深度限制的按叶子生长(leaf-wise)算法以及单边梯度采样算法,从而了降低原决策树方法及其衍生算法(如XGBoost)的误差,提升了计算精度,节省了时间与内存消耗,同时支持分布式运行,从而可以快速处理海量数据。如图3所示,以往按层生长(Level-wise)决策树生长策略改变为现在的带有深度限制的按叶生长,在当前叶子中寻找分裂增益最大的那一支,以此方式迭代。所以同以往相比,在计算次数相同的情况下其精度更高,误差更低。此外为防止出现叶子过深,还要设定max_depth参数以防止过拟合。

图3 带深度限制的Leaf-wise的叶子生长策略Fig.3 Leaf-wise foliage growth strategy with depth limitation
所以LightGBM算法速度更快,占用内存更小,随着处理数据数量增大,其优势也愈加凸显,因此尤其适合处理小颗粒度采样的回归问题,如延迟预测问题等。
2.2 基于LightGBM算法的延迟预测模型构造
近些年来,针对负荷预测、风电功率预测等时间序列的预测问题,大多采用由RNN改进的LSTM模型,能够对过去长期与短期数据行为均留下印象,增强了对数据间关联的挖掘。但代价就是为了更好地拟合,LSTM模型通常包含多层,而同时又要增加Dropout层以防止过拟合。如输入15分钟采样一次的负荷数据,每年就有4*24*365= 35 040个采样数据,再加上气温、降水、节假日等特征信息,训练模型要花费大量的时间与算力,普通的小型计算机CPU/GPU难以长期维持高负荷的迭代训练。因此,本文认为对于基于5G的配电自动化系统来说,更适合选择算力要求更低的LightGBM算法,同时其支持分布式并行计算的特点更是拓宽了系统未来的发展方向。
通常机器学习模型都会进行人工手动调参,以更好地对训练集进行拟合,降低预测误差。但是本文欲以实现实际场景中应用,首先终端时空因素均是不确定的,无法确定设备配置区域的日延迟曲线有何特性,数据的分布存在差异。另外配电网终端数量众多,无法穷尽人力去实现最优参数配置,因此引入贝叶斯优化加以辅助。
2.3 贝叶斯优化
贝叶斯优化(Bayesian Optimization,简称BO)也叫做主动优化。该方法本质上是基于模型的序贯优化,只有在当前轮次评估结束后才进行下一轮,能够根据未知目标函数f获取的信息选择下一个评估位置,以最少代价获取最优解。传统的网格调参 (Grid Search) 会从给定的超参数选择中搭配并遍历所有的超参数组合,找到这些组合中最优的方案。这种方式下每个组合都是独立计算,而下一次计算不会利用历史轮次的信息,因此造成大量算例的浪费,效率低下,同时对于非凸问题还容易陷入局部最优,而BO算法则克服了以上问题。
2.3.1 贝叶斯优化核心原理
机器学习可以看成一个黑盒子,只能知道其输入与输出是什么,难以确定中间过程的函数关系,因此转向一个可以表示并解决的函数上去。假设有函数f:x→R,欲在x⊆X内求得
(1)
其中,x表示模型超参数,而不是常规的输入变量,对于LightGBM算法,即为max_depth、num_leaves这类参数。贝叶斯优化的核心是利用条件概率,根据先验知识来获取随机变量的关联约束,式(2)为关键的贝叶斯定理。
(2)
下面以伪代码形式介绍贝叶斯优化算法实现过程。
Input:f,χ,S,M
D←InitSamples(f,x)
fori←|D| toTdo
p(y/x,D)←FitModel(M,D)
xi←[argmax]x⊆χS(x,p(y|x,D))
yi←f(xi) ΔExpensive step
D←D∪(x,yi)
end for
f表示机器学习模型,也就是输入一组超参数,可以得到输出值。X代表超参数空间。D为(x,y)组成的数据集,其中x为一个超参数组合,y表示对应输出。S表示采集函数(Acquisition Function),用来挑选x。M表示通过D训练后拟合出的模型,此处选择高斯模型为例。D←InitSamples(f,x)表示将输入输出加入到数据D中去,D=(x1,y1),…,(xn,yn)。T表示固定一个评估次数,防止过量计算f造成大量资源消耗。
2.3.2 贝叶斯优化框架
贝叶斯优化有两大要素,其一为概率模型代理,其二是采集函数。前者用于评价抽象的目标函数,后者则是利用代理模型的后验信息确定主动选择评估点的策略。
假设模型M服从高斯分布,即f~GP(μ,K),其中,GP表示高斯过程(Gaussian Processes),μ为均值,K为协方差kernel。xi←argmaxx⊆χS(x,p(y|x,D))表示假设的模型计算出来后,就模型来选择满足公式x*的参数,即xi,这就是采集函数(Acquisition Function)。经过选择超参xi,带入网络中训练,输出yi,并更新数据集D。
采集函数的功能是由已有数据集D1:t得出的后验分布构造,获取最大化增益的目标以选择下一个超参数组合xi+1。
αt(x;D1:t)=
(3)
常见的采集函数包括PI,EI,LCB及其组合,本文选择EI(Expected Improvement),如式(3)。该函数属基于提升的策略,相较于当前观测时刻最优函数值有所降低(因目标是求函数最小值)的位置作为下一个评估点。
2.4 K折(K-Fold)交叉验证
传统的机器学习,会将数据集按照6∶2∶2或是8∶1∶1的比例划分训练集、验证集与测试集,这被称为交叉验证(Cross-Validation)。但抽取样本的合理与否会影响训练结果的好坏,同时会存在数据集应用不充分的问题,而K折交叉验证就可以避免以上问题。如图4所示,它指的是将训练集分为K部分(通常为均分),每部分均有一次机会作为验证集进行训练,另外还有K-1次训练作为训练集,最后取平均误差作为泛化误差,这样一来,实现无重复抽样的同时保证了数据集得到了充分训练。
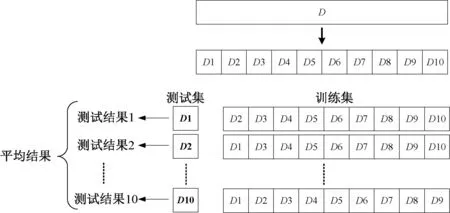
图4 K折交叉验证示意图Fig.4 Diagram of K-fold cross validation
出于对本文使用数据量的考量,这里结合两种方法,将数据集按照8∶1∶1的比例划分训练集、验证集与测试集,同时再在训练集上采用10折交叉验证,获取最好泛化特性。
2.5 动态加权组合
单一的机器学习模型总是有其弱势所在,因此很多人都会使用集成学习,它不是一个新的算法,而是一种技术框架,用以组合基础模型。目前有三种有代表性的的集成学习框架:Bagging,Boosting以及Stacking。LightGBM衍生自GBDT,而GBDT本身是一个Boosting集成学习方式,而在最后一个环节,本文将利用stacking思想来减小预测误差[25]。
Stacking核心是把强分类器进行强强联合,使得融合后的模型效果更强,其简化版为Linear blending,简单来说就是加权组合思想。对于某一预测问题的两个预测模型,设εit是第i个模型t时刻的误差,求得偏差矩阵E,其公式如公式(4)。
其中,m为数据集内元素个数,令R=[1,1,1,…,1]T,利用拉格朗日法可以获得最优权重配比(ω1,ω2,…,ωn)T=K= (E-1R)/(RTE-1R),其中ω1+ω2+…+ωn=1,ωi是各个模型的权重。
(4)
考虑到延迟波动较大,有相当一部分变化是无法预测的,因此这里结合实时数据进行动态调整。方法是将当前预测时刻的前一采样点实测数据充当第二个模型的预测结果,与LightGBM的预测结果进行组合,整体数列缺失的一位用相邻一个实测数据进行填充,最终求出最优权重配比。
2.6 预测流程
根据数据预处理过程中的可视化分析,能确定数据变化有一定的规律性,由此确定进行训练的特征量包括年份,月份,日期,每周第几日,小时,周末及节假日,温度。
首先对数据进行清洗预处理,过滤掉缺失信息与无效错误信息,也避免数据为0时会影响后续预测误差判定公式的运算。之后进行特征工程。特征数据分为数值型与类别型,由于LightGBM是由决策树模型衍生而来,树模型基于信息增益率、基尼指数等进行特征空间划分,其寻找的最优点是最优分裂点,因此过程是阶跃性不可导的,任何不影响排序结果的单调变换均不会影响模型,所以数据无须进行归一化;另外LightGBM算法对于类别特征有所优化,无需进行One-hot编码。导入Python内置datetime库,对于一周七天分别赋值0到6,另外对于周末节假日,工作日令其为0,其余则令为1。最后在所有特征处理后输入模型进行训练学习。
鉴于馈线自动化的分布式特性,以及不同终端地理分布有所差异的现实,提出集中-分布预测方式:由馈线自动化区域主站兼做机器学习的执行部分,每天向区域内终端下达次日预测延迟数值。各终端根据收到的数值,结合自身实测延迟,进行加权调整后作为自身下一阶段的故障搜索等待时间TW,预测流程图如图5所示。

图5 预测流程图Fig.5 Forecasting flow chart
3 算例分析
3.1 实验数据与平台介绍
本文使用河北省试点线路部署的5G智能分布式FA的外场测试环境[26],通过运营商提供的CPE挂载测试出线路运行期间5G终端的历史延迟数据。试点线路架设初期,该地区5G用户较少,SA组网的架构中可以获得与实验室相当的优秀延迟数据。但随着5G用户增多,该区域原有的5G基站与承载网负载大大增加,加上高频基站本身覆盖范围较小,使得后期测试的延迟整体有所提高,且波动较大,适合作为本文提出方法的测试数据集。选取2020年到2021年共2年的延迟数据,以及对应的温度记录,采样颗粒度为1小时,一天共产生24组数据。
本文采用的硬件平台为 Intel Core i7-6700HQ CPU和 NVDIA GTX 965M GPU。软件平台基于Python 3.8版本实现。
3.2 验证评估标准
延迟预测问题属于机器学习里的回归问题,因此可以选择判定系数R2/MAPE/RMSE/MAE等多种指标,在这里我们选择平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)与均方根误差(Root Mean Square Error,RMSE)作为横向比较模型预测精度的指标,二者公式如下:
(5)
(6)

前者衡量的是预测值偏离真实值的相对大小,结果用百分比表示,而后者则是真实值与预测结果的绝对偏离情况,大小受数据量纲的不同而有不同,因此不同的数据集无法以相同的RMSE去比较,适合相同数据集上不同模型的训练结果进行横向比较。RMSE受极端值影响比较大,而延迟本身波动就是比较大的,因此搭配MAPE与RMSE一起,在功能上可以达到互补的效果。同时RMSE有开方计算,可以放大误差,对于离群数据更为敏感,能够突出较大的预测误差。二者数值均较小时,表示模型的预测结果较为准确。
在考量预测结果准确度的同时,还要兼顾模型训练与预测所消耗的时间,以更好地进行方案移植与推广应用。
3.3 数据集预测结果与分析
表1为2021年12月20日至24日连续4天不同模型预测结果与实际延迟值的对比数据。其中模型I为线性回归算法,模型II为随机森林回归,模型III为XGBoost算法,模型IV为LightGBM算法,模型V为本文提出的贝叶斯优化的LightGBM算法。由表可看出,本文所提方法的预测误差相较于其他三种方法是最小的,4天中第1、3、4天误差表现最好,其中MAPE相比排名第二的方法差距分别是1.2%,0.42%,0.19%。单日提升数值上来看相差不大,原因是该方法基于LightGBM算法,其本身性能就比较优异。
为评估各个模型中短期预测能力,选取连续三天作为样本进行预测并比较精度,结果如表2所示。由表2可以看出,当把观测窗口放大到3天之后,随机出现的延迟波动现象对于预测精度的影响就被缩小,于是模型V的优势就显现出来了,相较于其他方法更为稳定可靠。
结合图6可以看出,在一天24小时时间内,计及不可预测波动的情况下,本文提出方法对于实际曲线的预测更准,拟合效果更好。尤其在7~10时波峰突然增大时,该方法反应最及时,跟随效果最好,能捕捉到突然的不可测变化,很好地降低了保护装置闭锁的可能性。

表1 不同方法的单日预测精度比较

表2 连续三天中短期预测精度比较
需要指出的是,CPE与基站之间的空口传播过程是影响延迟波动的最大因素,虽然实现了较高的预测精度,但延迟的不可测波动仍然会影响实际保护动作。除提升基站覆盖密度,加大带宽等物理层面的手段,还可以通过优化上行调度、空口误码、提高优先级以及调整重传机制等手段进行基站参数优化配置,以更好地推动配网馈线自动化5G化进程。

图6 不同模型24小时预测对比Fig.6 Comparison of 24-hour forecasts from different models
验证过程采用训练epochs为5 000,10折交叉验证,以损失函数100次迭代中无明显下降为终止,训练预测时间如表3所示。可以看出由于增加了优化算法,本文提出方法时间消耗相较基础机器学习算法有所提高。但按照2.6节所提流程,现实中由主站来负责训练与预测,由各终端结合主站下达数值进行修正,频次仅为每天1次,所以每天需要的时间并不多,在该任务分配思路下,该训练预测时间并不算长,由此在原理上能够减轻终端的计算压力,更好实现方案移植与推广应用。

表3 不同模型预测与训练时间比较
4 结 论
本文提出一种基于贝叶斯优化LightGBM算法的主动式搜索时间调整方法,该方法能够自行求出最适合当前区域延迟分布特征的超参数配置方案,无需人工手动调参,同时最优权重配比方法能够根据上一采样点数据动态地调整下一个预测值。相较于原始机器学习算法,该方法能够有效地捕捉延迟的突变,跟随效果更好,预测精度更高。
后续考虑通过加入降水、电力负荷、人口数据等其他特征,并对各特征的重要度进行排序,得到影响延迟变化最重要的特征搭配。另外,计划通过尝试LSTM、GRU等神经网络来解决预测问题的方法,进一步挖掘时间信息。
