加入淘汰机制的改进麻雀搜索算法*

周建新，侯宏瑶，郑日成

（华北理工大学电气工程学院，河北 唐山 063000）

0 引言

近几年，参数优化问题受到了广泛的关注，而传统的优化方法（枚举法、牛顿法、单纯形法等）无法在短时间内求得最优解或近优解［1］。群智能算法（swa rm intelligence algorithm，SIA）的提出为传统的控制方法提供了全新的思路，其在各学科中都逐渐展示出了强大的效果。尤其在控制工程领域，成为了一种对非线性、高纬度系统寻找最优值的强有力手段。

SIA 是一种根据人为经验或者自然规律所构造的数值寻优方法，具有自组织、自学习、自适应能力，且能够在可接受的计算花费下给出一个较优的可行解［2］，对于求解不同类型的系统具有通用性。其主要原理是根据生物捕食、游走、迁徙等行为特征和自然法则，并依托计算机强大的数据处理能力来解决问题。基于其突出的优点，SIA 得到了迅速发展，近期提出乌鸦搜索算法（CSA）、海鸥优化算法（SOA）、灰狼算法（GWO）、鲸鱼优化算法（WOA）、蜻蜓算法（DA）等［3-7］。

麻雀搜索算法（SSA）由薛建凯于2020 年提出［8］，该算法较其他群智能优化算法，优点是原理比较简单、易于实现、速度快、收敛精度高。但同其他SIA一样都存在一些固有的问题，面对高纬度复杂函数模型寻优时，种群初始化时位置随机产生，所以迭代后期易出现多样性不足，导致全局搜索能力有所下降；由于其机制问题，当纬度增加时无法更好地平衡局部与全局搜索能力。虽相比于其他基础群智能算法，SSA 保持有较高的收敛速度，但仍有很大的改进空间。

针对这些在寻优效果上出现的问题，相关学者和工程人员对SSA 进行了一些改进，改进侧重点主要分为两部分：一是在初始化种群参数方面，二是在种群搜索与收敛机制方面。例如，高晨峰等提出了一种黄金正余弦和曲线自适应的多策略麻雀搜索算法［9］，采用Chebyshev 混沌映射，改善了种群多样性，并融合黄金正余弦算法，增加了发现者之间的信息交流，在更新公式中添加自适应权重改善了易陷入局部最优的问题。李爱莲等提出一种融合正余弦和柯西变异的麻雀搜索算法［10］，借助折射反向学习机制初始化种群，且在发现者、跟随者位置更新公式上加入了正余弦算法和柯西变异扰动策略，提高了算法寻找全局最优解的能力。尹德鑫等提出了一种多策略改进的麻雀搜索算法［11］，对步长因子动态调整，并在侦察预警麻雀的位置上引入了Levy 飞行，提高了算法整体的寻优效果。

上述针对SSA 的改进策略通过加入初始化方法，提高了全局搜索能力；对收敛机制的改善，解决了传统SSA 对于平衡全局搜索和局部收敛方面的缺点。但经实验，其在面对高纬度复杂系统寻优时，效果并不能完全满足要求，在性能方面仍具有很大的改进裕度。针对此问题，本文提出了一种加入2N分段Tent 混沌映射和末位淘汰机制的改进麻雀搜索算法（TESSA）。

首先，在种群位置初始化时采用2N分段Tent混沌映射，使其初始位置更加具有均匀性和遍历性，增加种群多样性，提高算法收敛速度与全局搜索能力。其次，在种群位置更新后期加入淘汰机制，加快局部收敛速度与精度，同时改进跟随者位置更新公式为一种非线性自适应扰动，更好地平衡了全局寻优与局部挖掘能力，整体上进一步提升了SSA在数值寻优方面的效果。

1 基本麻雀搜索算法（SSA）

SSA 是受麻雀种群的觅食与生存行为启发而产生的一种数值寻优算法。其种群中包含3 类个体，第1 类是适应度值较高的发现者，这些麻雀总会找到食物最为丰富的地点，并且会带领整个种群进行觅食行为。第2 类为跟随者，它们会监视发现者的觅食行为并与之争夺食物来提高自己的捕食率。第3 类为侦察者，当侦察者发现捕食者后立即发出报警信号，全体麻雀做出反捕食行为［12］。种群中每只麻雀的当前所在位置表示其对应解空间中的一个可行解。对于单只麻雀，有，其中，i表示当前麻雀编号。则种群中所有麻雀的位置可表示为：

其中，P 表示麻雀种群数量，d 为待求解问题维度；f（xP）表示每只麻雀所对应的适应度值，则麻雀种群所对应的适应度值为：

发现者的位置更新有两种方式，其分别如式（3）所示：

跟随者则会不断监视发现者的行为，一旦其发现了食物，跟随者会立马进行食物资源的争抢，其位置更新公式如式（4）所示：

另外，种群中还存在10%～20%的警觉者，当其意识到危险时，会靠近其他麻雀来降低自己被捕食的几率，其位置更新如式（5）所示：

其中，Xbest为全局最佳位置；β 为服从均值为0，方差为1 的正态分布随机数；K∈［-1，1］为一个随机数；ε 为极小常数，避免分母为0；fi为当前麻雀个体适应度值；fg与fw分别为当前全局最优和最差适应度值；当fi＞fg时，表示当前个体处于种群边缘，可能会受到捕食者的攻击；fi= fg时，表明此时位于中心的麻雀感知到了危险，它们需要不断靠近附近同伴，来减少自己被捕食的几率。

2 加入淘汰机制的麻雀搜索算法

2.1 2N 分段Tent 混沌映射

传统的SSA 随机产生初始种群位置，容易导致后期种群多样性降低，收敛速度变缓。而混沌映射有较好的均匀性与遍历性，其被广泛应用于各种算法当中。常见的有Sine 映射、Logistic 混沌映射、Circle 混沌映射等。

Tent 混沌映射具有对初值不敏感，分布均匀等特点。故本文采用以一种对其改进后的2N分段Tent混沌映射来对SSA 种群位置进行初始化［13］，提高种群多样性。其表达式如式（6）所示：

其中，2N为分段数；Xn+1为经过映射后的数值；h 为设定的（0，1）之间常数；当2N=1，即N=0 时，式（6）即为普通的Tent 混沌映射。Lyaponuv 指数常常用来判断系统的混沌性，其定义式为式（7）：

由式（7）计算出2NTent 混沌映射的Lyaponuv指数大于普通Tent 混沌映射。所以，2N越大，其对于SSA 种群位置的初始化则更具有随机性和遍历性。但同时随着指数N 不断增大，计算时间也会成倍增加，为了平衡种群多样性与搜索时间，选取2N=16。

2.2 加入淘汰机制

传统麻雀搜索算法中，种群会根据式（3）～式（5）不断更新自己的位置，以达到逐步寻优，但这种方式比较依赖与公式所定义的搜索范围和步长，导致算法迭代速度不太稳定。针对此问题，本文提出了一种在经过3 个公式的位置更新后，对此次迭代中所有个体加入淘汰机制来加强算法的收敛速度。

图1 2N=16 时Tent 映射分布Fig.1 Distribution of Tent mapping when 2N=16

2.2.1 淘汰个体位置更新策略

淘汰机制即通过计算此次迭代中所有麻雀个体所对应的适应度值，淘汰掉适应度值排在末位的M 只个体，由于其被淘汰，所以下一代个体位置会更加倾向于在上代最优值附近产生。新生成的个体位置按照式（8）进行更新：

2.2.2 自适应淘汰个体数量

由上述可知M 作为被淘汰个体的数量，其所设定的数值对平衡收敛速度与寻优精度具有重要意义。分别取M=0.2，M=0.4，测试函数如表1 所示，取最大迭代次数为100，种群数量为50，发现者所占比例为20%，警觉者比例为10%，其寻优效果如图2所示。

表1 F1 测试函数Table 1 F1 test function

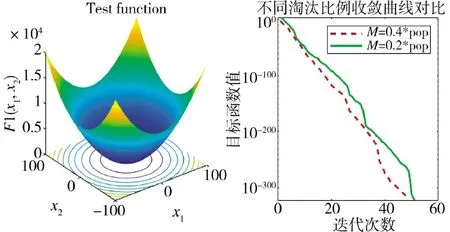
图2 不同淘汰比例下的收敛曲线Fig.2 Convergence curves under different elimination ratios

由图2 可知，虽然较大的M 会使算法收敛速度加快，但由于其不断在最优值附近产生固定的M 只新个体，容易导致全局搜索能力不足，迭代后期出现速度下降、无法收敛至极小值等问题，故并非M越大越好。

针对此问题，引入一种非线性自适应淘汰个体比例，即在初始迭代时对种群边缘的麻雀加大淘汰比例，节省搜索时间，在迭代后期逐渐减小，保持种群的多样性，其更新方式如式（10）所示：

其中，M 为淘汰个数；t 为当前迭代次数；Tmax为最大迭代次数；ω 为下降速率；Eli∈（0，0.5）为依据具体要求设定的初始淘汰比例；P 为种群总数；

取Tmax=500，ω 为1.5，Eli 分别为0.2 与0.4，P 为100，其自适应淘汰曲线如图3 所示。

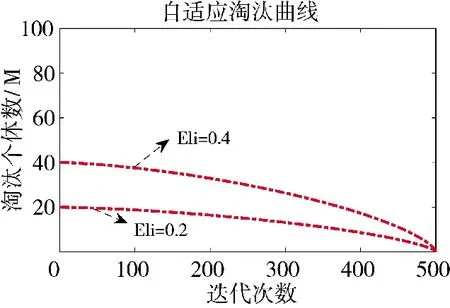
图3 不同初始淘汰比例下的淘汰曲线Fig.3 Elimination curves under different initial elimination ratios

2.3 基于柯西变异的跟随者位置更新

经过加入淘汰机制，每次迭代适应度最差的一部分麻雀个体会被直接淘汰，在最优值附近产生，所以其在下一代位置更新时，大概率会进入发现者群体中，并执行式（3），由于麻雀种群中发现者与跟随者的比例是不变的，故相应的一部分发现者会变为跟随者并执行式（4），并且跟随者会在发现者附近觅食。为了平衡算法前期淘汰机制不断在最优值附近产生的缺陷、防止算法陷入局部最优值，受文献［10］启发改进跟随者位置更新公式，用来提高全局搜索能力，其更新方式如式（11）。

当i＞n/2 时，表明当前个体处于种群边缘，其适应度值排在末位，所以要加大其搜索范围，使其向更广阔的区域进行觅食。

而对于适应度值排在靠前位置的跟随者，引入柯西变异。Cauchy（0，1）为标准的柯西分布函数，比标准正态分布能产生更大的扰动，使其在最优值附近进行相对广泛的搜索。TESSA 算法流程如下页图4 所示。

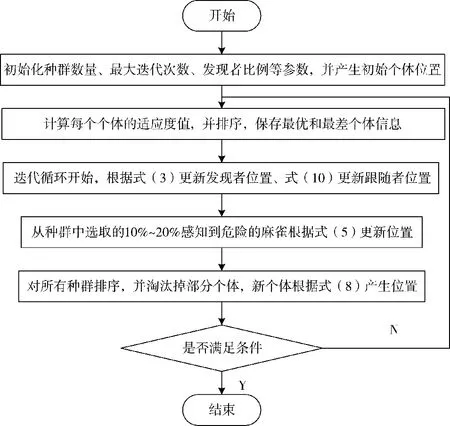
图4 TESSA 算法流程图Fig.4 TESSA algorithm flowchart

3 TESSA 算法性能测试

为验证TESSA 对于提高函数寻优速度、寻优精度和稳定性的效果，选取灰狼优化算法（GWO）、粒子群优化算法（PSO）、麻雀搜索算法（SSA）、融合正余弦和柯西变异的麻雀搜索算法（SCSSA）、与本文加入淘汰机制的麻雀搜索算法（TESSA）在6 个测试函数上进行仿真比较［10］。

3.1 测试函数选取

选取6 个测试函数进行仿真，为了确保算法性能的稳定性，其中f1～f4为单峰测试函数，其搜索范围分别为［-100，100］、［-10，10］、［-100，100］、［-100，100］，f5、f6为多峰测试函数，其搜索范围为［-5.12，5.12］、［-32，32］。在单峰函数上的测试可以用来检测算法的寻优速度与精度。在多峰函数上，则用来验证其跳出局部最优的能力。测试函数表达式如表2 所示。

表2 测试函数表达式Table 2 Test function expression

3.2 TESSA 性能对比分析

将加入淘汰机制的麻雀搜索算法（TESSA）与融合正余弦和柯西变异的麻雀算法（SCSSA）［10］、基本麻雀算法（SSA）［8］、粒子群算法（PSO）［14］、灰狼算法（GWO）［5］在6 个基准函数上进行寻优测试，各个算法公共参数即种群数量均设置为50，最大迭代次数Tmax为200，搜索范围依据测试函数上下界。5 种算法参数选取如表3 所示时，经实验，各个算法参数选取在6 个测试函数上均能达到其自身寻优仿真的最佳效果。

表3 算法参数设置Table 3 Algorithm parameter settings

取最优值、平均值、标准差作为实验结果数据，最优值反映了算法跳出局部最优解的能力，平均值体现了寻优精度，标准差则代表了算法的稳定性。

由于函数维度变化时，对于算法寻优能力的要求会增大，每个维度之间也会有一定的相互干扰，为了证明不同维度下TESSA 的优越性，函数求解维度分别设置为30 和80。各个算法独立运行50 次，以降低实验的偶然性。仿真采用环境为intel-i5 处理器，2.30 GHz，16 GB 内存，MATLAB R2018b。

5 种算法在6 个测试函数下独立运行50 次的实验结果如下页表4 所示。由表4 中的仿真数据可以看出：对于单峰测试函数f1～f3，TESSA 都能收敛至最优值，且平均值与标准差均为0，而SCSSA 在f2中未能达到最佳效果，这展示出了TESSA 良好的寻优精度。对于f4中的高维空间，TESSA 最优值虽与SCSSA 相差一个数量级，但其平均值与标准差效果较好，这体现出TESSA 在稳定性方面的优势。在f5、f6多峰测试函数中，TESSA、SCSSA、SSA 的寻优精度都达到了最优，且标准差都为0，故麻雀搜索算法相较于灰狼算法和粒子群算法具有更佳的函数寻优能力。

表4 算法性能比较Table 4 Comparison of algorithm performance

为体现TESSA 较其他两种麻雀搜索算法在收敛速度方面的优势，画出了各算法在6 个测试函数维度均为30 时的迭代收敛曲线，如第71 页图5 所示。

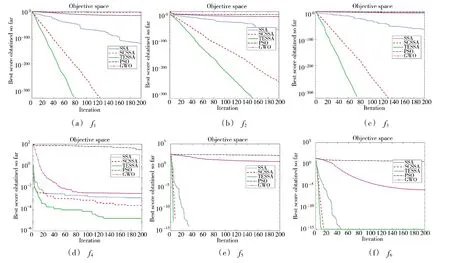
图5 5 种算法在函数上的收敛曲线Fig.5 Convergence curve of five kinds of algorithms on functions

图5（a）～图5（d）为单峰测试函数的算法收敛曲线，图5（e）和图5（f）为多峰测试函数收敛曲线。由图5（a）可以看出当TESSA 和SCSSA 都能够收敛至最优值时，TESSA 的收敛速度更快，在79 代便收敛至极小值，而SCSSA 需要迭代126 代。由图5（b）可知，在5 种算法中，只有TESSA 达到最优值，体现了其寻优精度。图5（d）中，当5 种算法都未能寻优至最优值时，TESSA 仍然保持着与其他算法相比更快的收敛速度与全局搜索能力。从图5（e）与图5（f）中则看出在多峰函数测试下，虽然SCSSA 改善了传统麻雀算法的一些缺陷，性能有大幅提高，但TSEEA 仍在保持精度与稳定性的同时具有更快的寻优速度。

3.3 Wilcoxon 秩和检验

威尔科克森（Wilcoxon）秩和检验是一种非参数统计检验方法，本文用来检测TESSA 与其他4 种算法是否具有非随机性的显著优势。Wilcoxon 秩和检验将在5%的显著性水平下进行检验，当检验结果P＜0.05 时，拒绝H0假说，表明对比的两种优化算法在寻优能力上存在着显著差别；当P ＞0.05 时，接受H0假说，表明进行对比的两种算法在寻优效果上没有区别。

在6 个测试函数（30 维）上TESSA 算法与其他4 种算法的Wilcoxon 秩和检验P 值如表5 所示；由表5 结果可知，大多数P 值＜0.05，证明TESSA 与其他算法具有显著性差异。在f1～f4中P 值均大幅小于5%，故TESSA 寻优性能高于SCSSA、SSA、PSO、WOA。在f5、f6中TESSA 较SCSSA 寻优效果差异不明显，但在其他4 种测试函数中性能显著优于SCSSA，可以说明改进的有效性。

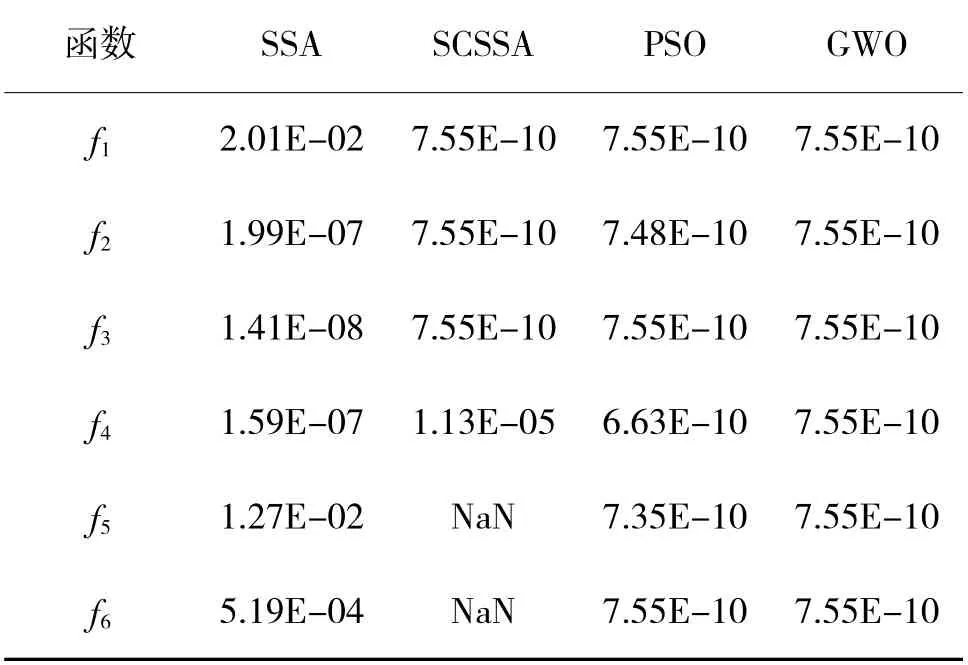
表5 Wilcoxon 秩和检验的P 值Table 5 P-values of Wilcoxon rank sum test

4 结论

本文对基本麻雀搜索算法（SSA）在高纬复杂系统中收敛速度下降，无法平衡局部收敛与全局搜索等问题，提出了一种加入淘汰机制的麻雀搜索算法（TESSA）。在初始化种群位置时，引入分段Tent 混沌映射，来提高种群的多样性。在跟随者位置处，加入了一种基于柯西变异的自适应位置更新公式。最后在当代种群位置更新完后，增加了淘汰机制，并采用了非线性的淘汰个体比例。经过与其他4 种算法在6 个基准函数上的测试仿真后，结果表明，TESSA 改善了传统麻雀搜索算法的诸多问题，平衡了收敛速度与寻优精度，相较于其他改进后的麻雀搜索算法有一定性能方面上的提升。

在未来进一步的深入学习中，重点研究方向为将TESSA 应用于实际，优化工程中的控制、解耦等方面，证明其解决具体问题的有效性。