一类含有有色噪声的鲁棒非线性扩展状态估计*

师卫国，朱可欣，董燕飞，祁 林，贺 伟，侯 宁

（河南城建学院电气与控制工程学院，河南 平顶山 467036）

0 引言

状态估计问题作为控制和信号处理领域的基础研究课题之一，在过去几十年中被学者们广泛研究。状态估计的主要思想是根据系统模型和测量输出信号对给定系统的内部状态进行估计，从而实现准确预测和控制系统。到目前为止，状态估计器已在飞机跟踪、智能电网和生物过程监控等领域成功应用［1-3］。随着科技的进步，对于状态估计方法和系统噪声约束的研究取得了新的进展，H∞估计、分布式状态估计、滚动时域估计和噪声处理等方案已得到广泛研究，并应用于工程实验［4-7］。

近年来，非线性系统因其在理论分析和实际应用中的重要性引起人们的广泛关注。在大多数应用中，非线性变量的存在使得系统性能难以得到精确的分析和控制，如果处理不当，可能会降低系统性能，甚至导致不稳定［8-9］。对非线性系统的状态估计，已经进行了许多方案研究，例如自适应控制、扩展卡尔曼滤波和粒子滤波［10-12］。文献［13］针对一类具有全状态约束和未知时滞的非线性随机系统，提出了一种自适应神经网络控制器。将系统转化为非线性映射的约束自由系统，补偿未知时滞不确定性，利用神经网络逼近设计过程中出现的未知非线性函数，该方法能够实现闭环系统信号的最终有界性和全状态约束。扩展状态观测器是一类用于不确定非线性系统输出反馈控制的高增益观测器，本文提出了一种新的级联设计，将饱和度转变为内部变量，以限制最大实现增益，相比标准观测器的输出，反馈控制具有更强的不确定性估计、补偿能力和收敛性［14］。文献［15］针对一些强的非线性系统，通过将非线性函数扩展成为系统状态，设置函数变化率上界，降低非线性干扰对系统的影响，该方法在估计性能方面具有很好的效果。

网络化系统通过共享的通信通道将系统和控制器连接起来，可以轻松构成新的体系结构，同时具有成本优势，因而被广泛应用于交通、医疗、电力系统等领域［16-18］。然而，当大量系统同时共享一个公共通信通道时，网络系统中的通信容量限制是不可避免的。为了克服这一问题，在过去几十年中，研究人员对传输调度问题做了许多工作，为网络系统设计了不同种类的传输调度协议。文献［19］研究了在网络中节点间通信带宽有限，在节点间交换的信息必须量化的情况下，求解分布式凸优化问题的梯度方法。提出了一种改进的基于共识的梯度方法来解决这类问题，研究了系统的收敛性，并给出了收敛速度。文献［20］采用轮询协议周期性地发送测量数据，克服了通信容量的限制。由于调度协议改变了测量结构，导致循环调度诱导的周期性扩展状态系统不可观测，本文建立了周期扩展状态系统的可观测性充要条件。文献［21］设计了一种动态事件触发器，使控制器只在触发时刻解决优化问题，触发阈值与反馈策略的插值系数相关，并通过优化确定。利用插值技术构造反馈策略，对原系统约束进行紧化，满足鲁棒约束。

基于上述说明，本文主要研究约束信道下的非线性不确定系统的状态估计问题，贡献如下：

1）创新测量信息逐差法处理有色噪声的相关性问题，解决标准卡尔曼滤波无法处理相关噪声的难题；

2）通过使用对数量化器降低通信网络的传输压力，利用矩阵不等式消除量化误差，保证系统的鲁棒性；

3）将非线性项作为系统状态，构造扩展状态系统，设计扩展状态估计器。通过Young’s 不等式求解先验估计误差协方差上界和估计误差协方差上界，在此基础上优化估计器增益。此方法处理非线性更加简单，针对强非线性系统仍然具有良好的估计效果。

1 问题描述

1.1 系统模型

文中，考虑如下的非线性时变系统：

1.2 有色噪声

有色噪声vk满足下列条件：

假设1 噪声ωk和uk为互不相关的白噪声，满足：

其中，δkj为Kronecker 函数：

1.3 非线性扰动

1.4 量化测量

为了降低通信通道的传输压力，本文采用对数量化器对测量信息进行处理，对数量化器的量化集合为：

其中，0＜ρj＜1 为量化密度，u0为初始向量，n 为量化级数。

同时，测量方程满足的下列映射关系：

根据对数量化器的定义，测量信息可以表示为：

引理3 给定实数矩阵B，X，等式满足下列特点［24］：

2 鲁棒扩展状态估计器设计

在进行鲁棒扩展状态估计器设计之前，先对系统作出下列假设：

假设4 非线性函数的变化率gi（xk）满足：

根据卡尔曼滤波的定义，结合系统测量方程，分别给出先验估计值、后验估计值、先验估计误差协方差和后验估计误差协方差的定义：

结合定义和系统的测量信息，鲁棒扩展状态估计器可以设计为：

其中，Kk+1表示状态估计器增益。

以上工作内容为接下来鲁棒扩展状态估计器设计做了很好的铺垫，在估计器设计过程中，计算增益矩阵Kk和误差协方差上界是非常重要的环节，接下来的主要任务便是通过分析和计算估计误差协方差，得到这些参数，完成状态估计器设计。

其中，

Step 1 解决式（19）中的交叉项，采用引理1，得到下列不等式：

然后，将式（24）和式（25）的结果代入式（19），下列等式成立：

Step 2 首先利用引理1 解决式（20）中的交叉项，再采用引理2 处理量化误差。

接下来，采用引理2 处理对数量化器造成的量化误差：

将以上结果代入式（20），可以得到下列不等式：

其中，

其中，

至此，定理1 证明完毕。

定理2 利用定理1 计算的结果，计算增益矩阵Kk+1的更新方程为：

证明

至此，定理2 证明完毕。

3 仿真实验

在本章中，通过仿真数例来验证所设计的鲁棒扩展状态估计方案的有效性。

3.1 系统说明

案例选取的非线性函数如下：

系统矩阵选取：

估计器参数选取：

3.2 仿真方案

接下来，将通过6 个仿真方案，对设计的估计器性能进行对比分析，充分论证鲁棒非线性时变扩展状态估计算法的合理性和有效性。

方案1：根据非线性时不变系统，设计鲁棒非线性状态估计器，系统参数选取如下：

方案2：根据非线性时变系统，利用对数量化器处理测量信息，设计鲁棒非线性扩展状态估计算法，量化密度为ρ=0.5，初始向量u0=100。

然后利用控制变量法，对比鲁棒非线性扩展状态估计器性能，具体方案如下：

方案3：量化密度为ρ=0.3，初始向量u0=100；

方案4：量化密度为ρ=0.9，初始向量u0=100。

方案5：量化密度为ρ=0.5，初始向量u0=100；

方案6：量化密度为ρ=0.5，初始向量u0=10。

为了验证本次估计算法对非线性系统的一定普适性，特给出方案7 进行说明，采用的非线性函数如下：

3.3 仿真效果

图1 状态x1，k 的实际值和估计值（方案1）Fig.1 Actual and estimated values of state x1，k（Scheme 1）

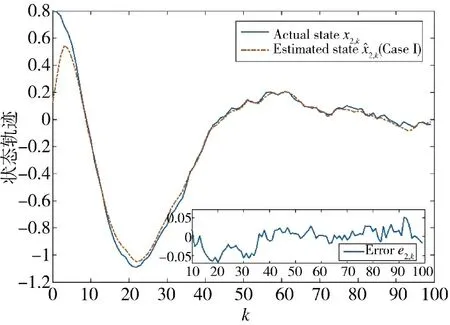
图2 状态x2，k 的实际值和估计值（方案1）Fig.2 Actual and estimated values of state x2，k（Scheme 1）

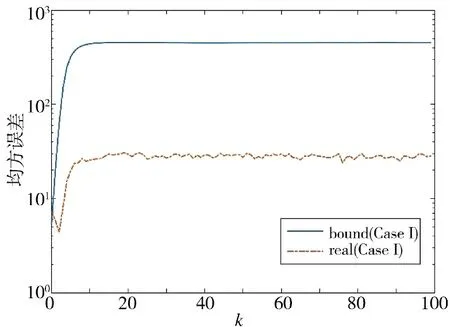
图3 估计误差协方差及其上界（方案1）Fig.3 Estimation error covariance and its upper bound（Scheme 1）

从图4 ～图7 可以看出，方案2 设计的估计算法具有良好的估计效果，由于是基于非线性时变系统进行设计，其工程价值明显高于时不变系统。对比方案1，在估计误差协方差方面，时变系统的波动性和数值均大于时不变系统，这是系统本身存在的差异，同样表明了估计器设计的合理性。

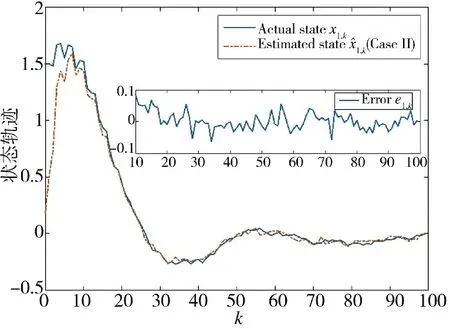
图4 状态x1，k 的实际值和估计值（方案2）Fig.4 Actual and estimated values of state x1，k（Scheme 2）

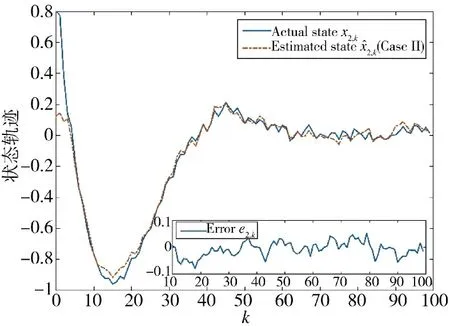
图5 状态x2，k 的实际值和估计值（方案2）Fig.5 Actual and estimated values of state x2，k（Scheme 2）

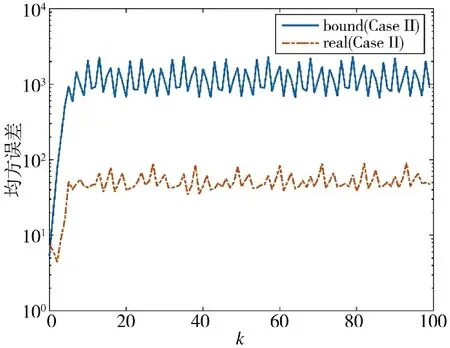
图6 估计误差协方差及其上界（方案2）Fig.6 Estimation error covariance and its upper bound（Scheme 2）

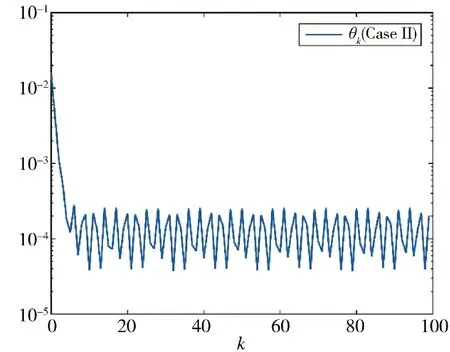
图7 参数θk 的变化情况（方案2）Fig.7 Variation of parameter θk（Scheme 2）

从图8～图11 可以得到，在方案3 和方案4 的估计效果对比中，量化密度小的估计误差大于量化密度大的估计误差，充分说明量化密度对于系统性能的影响。从图11 的估计误差协方差可以清晰地看出，量化密度大的估计误差协方差更小，性能更优。

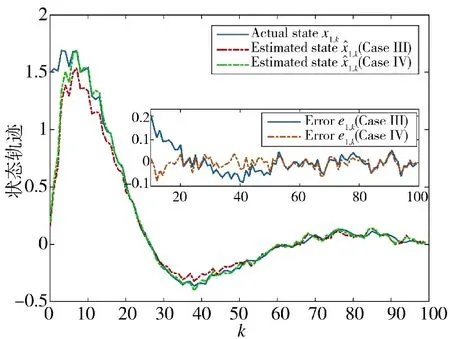
图8 状态x1，k 的实际值和估计值（方案3 和方案4）Fig.8 Actual and estimated values of state x1，k（Scheme 3 and Scheme 4）

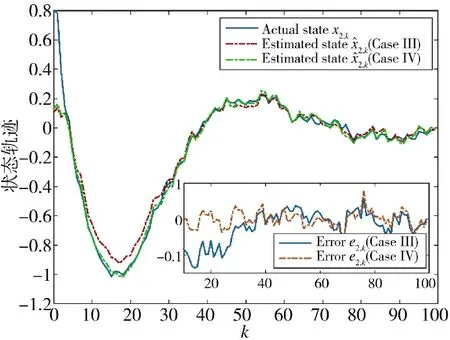
图9 状态x2，k 的实际值和估计值（方案3 和方案4）Fig.9 Actual and estimated values of state x2，k（Scheme 3 and Scheme 4）

图10 状态x3，k 的实际值和估计值（方案3 和方案4）Fig.10 Actual and estimated values of state x3，k（Scheme 3 and Scheme 4）

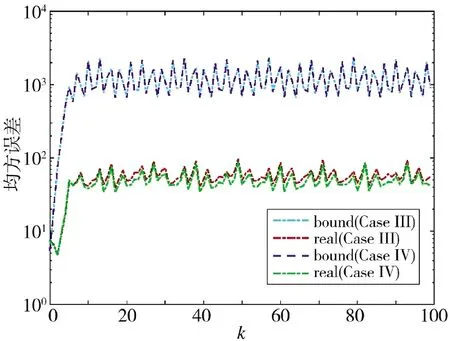
图11 估计误差协方差及其上界（方案3 和方案4）Fig.11 Estimation error covariance and its upper bound（Scheme 3 and Scheme 4）

通过图12～图15 的对比，可以看出初始向量对估计算法的影响不大。两种方案中，方案5 的初始向量较大，在估计状态、估计误差和协方差方面的值还是小于方案6，说明初始向量可以影响性能，且相对较大性能更好。

图12 状态x1，k 的实际值和估计值（方案5 和方案6）Fig.12 Actual and estimated values of state x1，k（Scheme 5 and Scheme 6）

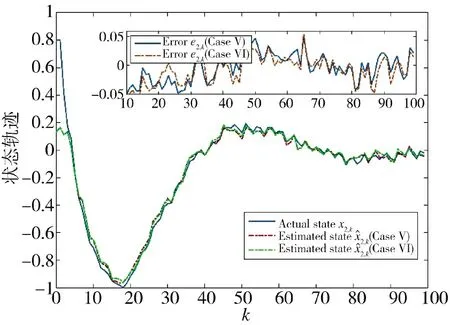
图13 状态x2，k 的实际值和估计值（方案5 和方案6）Fig.13 Actual and estimated values of state x2，k（Scheme 5 and Scheme 6）

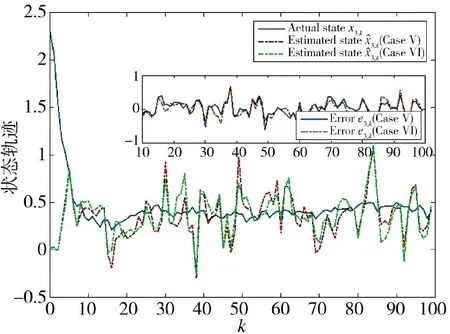
图14 状态x3，k 的实际值和估计值（方案5 和方案6）Fig.14 Actual and estimated values of state x3，k（Scheme 5 and Scheme 6）

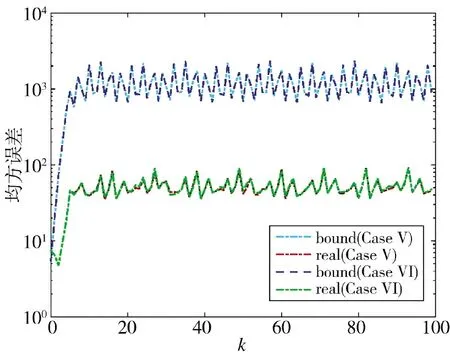
图15 估计误差协方差及其上界（方案5 和方案6）Fig.15 Estimation error covariance and its upper bound（Scheme 5 and Scheme 6）

通过图16～图19 可以得到，算法针对不同的非线性系统同样具有不错的估计效果。系统的各个状态均能够被跟踪，同时估计误差协方差具有稳定上界，说明所设计的估计器具备一定普适性和合理性。

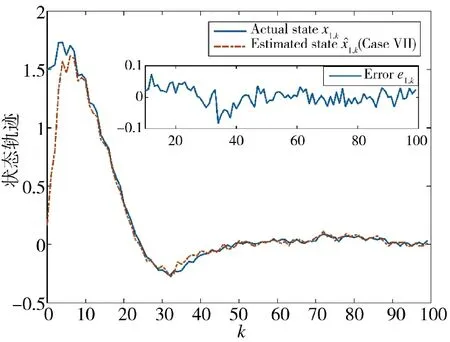
图16 状态x1，k 的实际值和估计值（方案7）Fig.16 Actual and estimated values of state x1，k（Scheme 7）

图17 状态x2，k 的实际值和估计值（方案7）Fig.17 Actual and estimated values of state x2，k（Scheme 7）

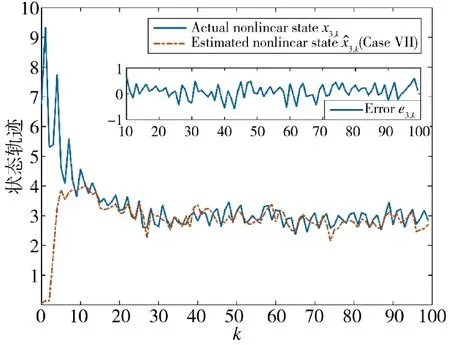
图18 状态x3，k 的实际值和估计值（方案7）Fig.18 Actual and estimated values of state x3，k（Scheme 7）

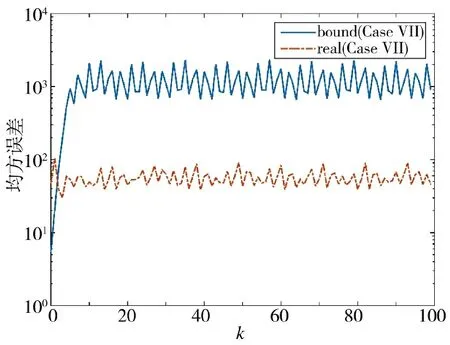
图19 估计误差协方差及其上界（方案7）Fig.19 Estimation error covariance and its upper bound（Scheme 7）

4 结论

在本文中，创新地使用扩展状态方式处理系统非线性，设计了能够处理有色噪声和带宽受限的鲁棒扩展状态估计算法。针对标准卡尔曼滤波无法处理有色噪声的问题，总结出了测量信息逐差法；考虑到网络化系统存在通信受限情况，采用对数量化器进行信息处理，提高网络传输安全性；创新非线性系统分析方法，利用扩展状态方式进行解决。扩展状态卡尔曼滤波在处理强非线性方面具有很好的效果，同时运用非线性变化率的界作为约束条件，降低了非线性系统分析研究的保守性。算法给出了估计误差协方差上界的计算方法，实现了增益的实时优化。通过仿真实例验证了所研究算法的合理性、有效性和普适性。