融合光学椭率判据的自由曲面望远镜设计方法

黄静，许宁晏，邹宇通，乔文佑，伦旭磊，孔梅梅，陆辰熙，高志山，袁群

（1 南京理工大学 电子工程与光电技术学院， 南京 210094） （2 南京邮电大学 电子与光学工程学院、柔性电子（未来技术）学院， 南京 210023）

0 引言

观测弱引力透镜效应是精确测量太空中暗物质和暗能量的重要方法，天体和星系经望远镜成像后形成的圆形衍射斑，会因为弱引力透镜效应而具有一定椭率［1］。弱引力透镜效应对星系成像点扩散函数（Point Spread Function，PSF）椭率的影响非常微弱，而望远镜系统自身的像差却又极易导致其光学椭率变化，干扰暗物质的检测。因此，为满足探测弱引力透镜效应及暗物质的要求，必须对望远镜系统自身椭率加以控制。

椭率是一种比波像差、MTF 等传统评价指标要求更苛刻的综合判据。以点列图为例，像质指标要求对点列图的均方根（Root Mean Square，RMS）值进行优化控制，并不要求点列图分布的形状，但光学椭率指标则要求点列图的分布需旋转对称。常规光学设计以波像差或点列图为指标进行优化，而波像差或点列图良好并不能代表系统的椭率也得到了较好的控制。光学设计软件无法直接将椭率作为优化指标，仍是以波像差等综合评价指标作为评价函数，在光学设计完成后，再根据PSF 的分布计算光学椭率，查验其是否满足设计指标要求，如不满足要求，还需重新迭代进行优化设计。当前的设计方法没有将光学椭率性能判据融入到空间望远镜设计过程中，缺乏对与椭率相关联的非旋转对称像差优化控制的方法。

传统优化设计方法采用面型逐步升级的方式，按照从低阶项到高阶项的顺序逐步添加自由曲面面型项，并在添加过程中持续保持系统结构变量可变化。该方法缺乏对系统当前像差的优化针对性，且盲目地在多个表面上使用自由曲面项将会导致像差校正退化及不必要的自由曲面偏离。自由曲面优化设计过程通常是指优先校正的像差类型和自由曲面面型变量的添加方式，以Zernike 面型为例，设计者需要考虑每轮迭代优化时添加的Zernike 项类型及添加的表面。2005 年，THOMPSON K 等提出了节点像差理论，分析了光学系统像差节点的分布特性，为自由曲面像差优化提供了理论指导［2］；2018 年，ROLLAND J 等解析了系统像差特性与自由曲面面型的关联关系，选择使用自由曲面进行校正的可能性最大的初始结构作为优化起始点，以波像差为优化指标，通过像差理论来确定每一步需要添加的Zernike 项及添加的表面［3］；2014 年，张新等利用精确的光学PSF 模型，对椭率的特性进行建模和分析，计算出了全视场的光学椭率分布，通过对波像差的控制间接平衡了全视场椭率，完成了无遮拦离轴望远镜的设计［4］；2017 年，史浩东等分析了自由曲面对光瞳离轴系统像差节点分布的影响，通过对像差节点位置的控制平衡了由系统光瞳离轴引起的非对称像差，使得对椭率的控制更有针对性［5］；2020 年，罗敬等基于偏振光线追迹，分析了偏振像差对望远镜光学椭率的影响［6］。前人基于像差理论的指导，以波像差为优化指标研究了自由曲面项的添加方式，讨论了波像差对椭率的影响并尝试通过波像差的分布间接控制椭率，但尚未将光学椭率融入到设计过程中进行直接控制。

本文围绕上述问题，在光学设计软件使用方面，针对传统光学设计无法直接将椭率作为评价指标的难题，经MZDDE 工具集实现光学设计软件Zemax 与数值计算软件Matlab 间的椭率数值交互，将天文椭率指标纳入到光学设计正向过程中；在设计理论与方法方面，以像差与椭率的关联关系为基础，结合像差理论指导与椭率相关联的非旋转对称像差校正，通过分析优化过程中非旋转对称像差与椭率节点分布的关联关系，求解利于椭率指标实现的自由曲面像差优先控制的必要分量，据此建立波像差和光学椭率的融合型评价函数体系，继而实现波像差与椭率之间的联合优化，并在自由曲面离轴三反射式望远系统中开展设计验证。

1 波像差与椭率的融合型评价函数体系

1.1 PSF 椭率表征

PSF 是反映望远镜成像质量的一项重要指标参数。根据PSF 的分布可以计算半高全宽、椭率以及80%能量圈半径等性能指标［7-8］。

椭率的要求实际上是对PSF 的要求，由PSF 计算得出的椭率表征了PSF 的大小、形状和空间分布，并且其特性由PSF 随时间和空间的变化来决定。PSF 是对光瞳函数的快速傅里叶变换（Fast Fourier Transform，FFT），可以定义为［9］

式中，A是孔径函数，dOPD是光程差，λ是主波长。

天文椭率描述了天体和星系由于弱引力透镜效应而在望远镜像面形成衍射斑的扁平程度，由0°/90°方向上的椭率e1和±45°方向上的椭率e2两个分量构成，椭率e的大小为两个分量e1和e2的均方根［10-12］，即

式中，Qxx、Qxy、Qyy为PSF 的二阶加权矩［13-14］，定义为

式中，I（x， y）为像面点（x， y）的PSF 值，W（x， y）是PSF 半高全宽（Full Width at Half Maxima，FWHM）的高斯加权函数，xˉ和yˉ是像面质心［15］，即

1.2 MZDDE 交互与椭率分布

MZDDE 是用Matlab 脚本编写的利用动态数据交换 （Dynamic Data Exchange，DDE）技术与Zemax 光学设计软件进行数据交互的工具集，是Matlab 与Zemax 的动态链接库，可完成动态数据交换，实现Zemax 扩展功能。利用MZDDE 交互实现Zemax 评价函数中光学椭率的融入，数据传递示意图如图1 所示。

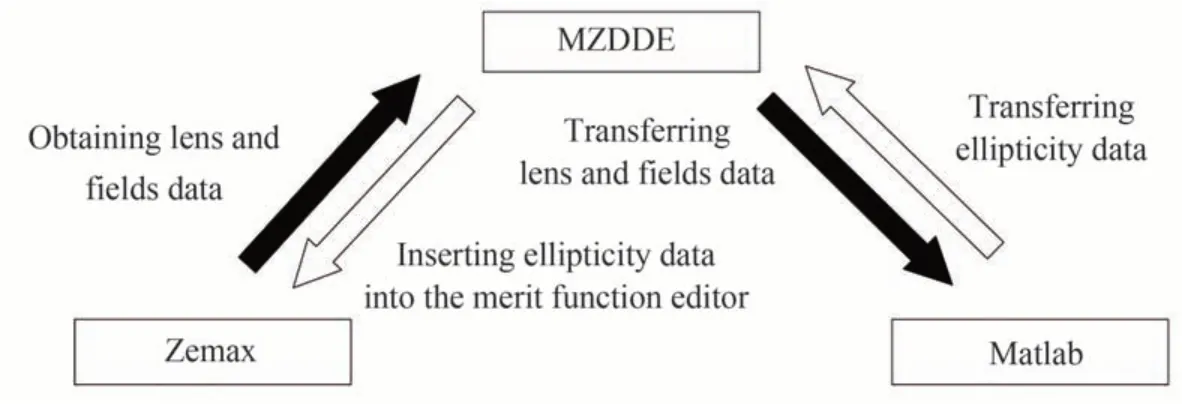
图1 MZDDE 数据传递示意图Fig. 1 Schematic diagram of data transmission for MZDDE

在Zemax 光学设计软件中采用快速傅立叶变换（FFT）方法计算出单个视场点扩散函数PSF，通过MZDDE 读取Zemax 存储的PSF 数据文件，经由Matlab 计算出单视场采样点椭率数值，进而拓展到全视场椭率分布，得到需要控制的全视场椭率最大值与平均值，再将其返回到Zemax 评价函数中。全视场椭率计算流程如图2 所示。

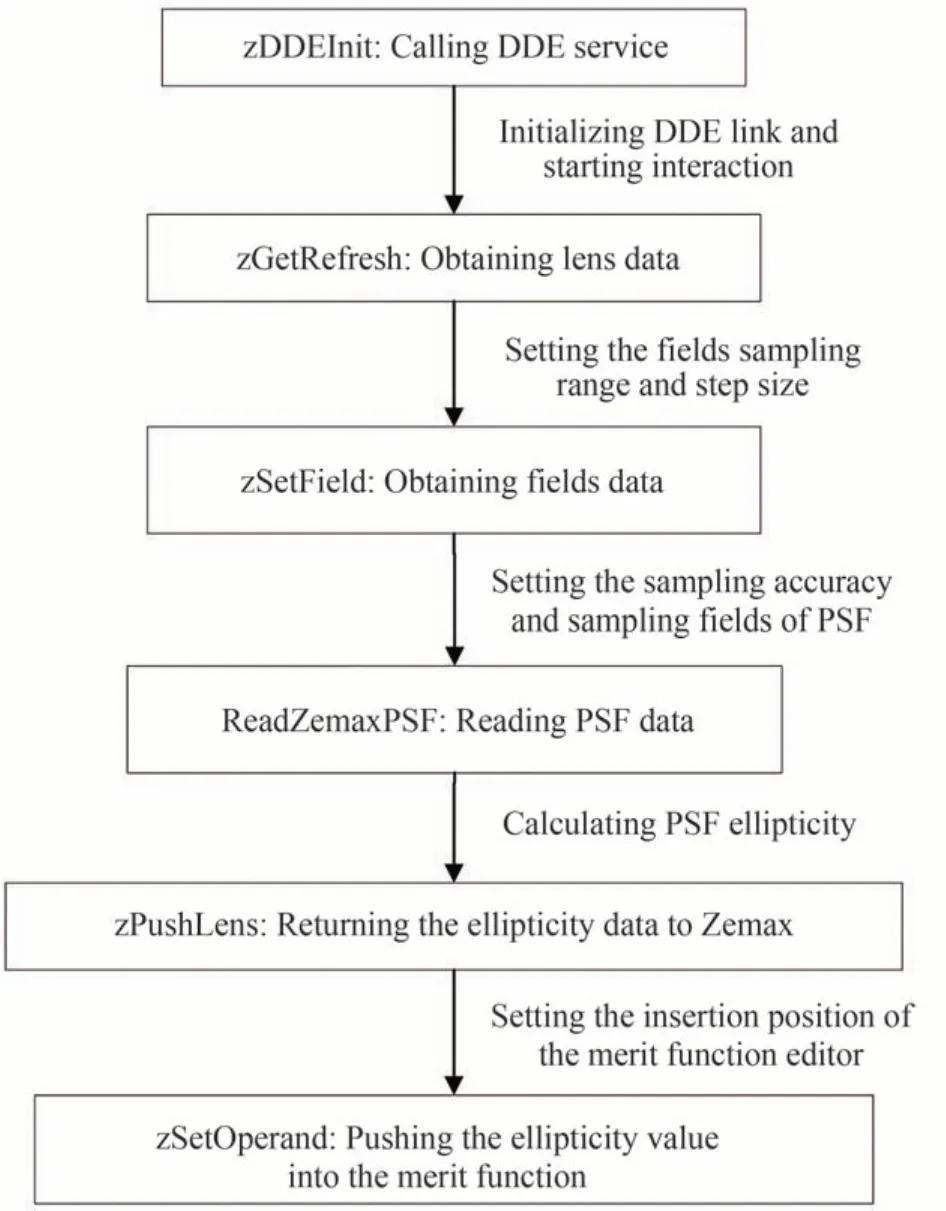
图2 全视场椭率计算流程Fig. 2 The calculation process of full field ellipticity

在调用访问Zemax DDE 服务器的任何函数之前，需初始化DDE 链接，使用zDDEInit 函数呼叫DDE 服务。通过zGetRefresh 函数将Zemax 光学系统的镜头数据从透镜数据编辑器中复制到服务器的存储副本当中，利用zSetField 函数获取特定视场的视场数据，需要根据实际光学系统的视场范围设置，以合适的采样步长确定视场采样点，视场采样步长越小，得到的椭率数据点越多，全视场椭率分布越连贯平缓。像面采样间隔决定了PSF 的采样精度及PSF 椭率的计算精度，PSF 采样时像面采样间隔越小，计算的椭率数值越精确，运行速度也相对越慢。

当采样循环运行时，在预先设定好的指定文件夹保存每个采样点的PSF 数据文件。ReadZemaxPSF 函数读取保存的PSF 文件，计算每个采样点的椭率数值，并算出采样点集合中椭率最大值、平均值以及均方根值。此时椭率值位于DDE 服务中，zPushLens 将椭率数值返回至Zemax 光学设计软件中，zSetOperand 函数将数据插入Zemax 中的评价函数编辑器，方便系统进行后续优化。

1.3 波像差与椭率的融合型设计方法

常规光学设计方法以像质为优化指标间接校正椭率，以降低系统总像差为目标，缺乏对与椭率相关联的非旋转对称像差校正的针对性，且尚未实现对光学椭率的直接控制。

将光学椭率融入到光学设计的正向过程中，构建波像差与椭率的融合型评价函数体系，可以实现对椭率的直接控制和优化。为了兼顾波像差和椭率的有效校正，在确定设计流程之前，主要有如下几点考虑：

1）当光学系统波像差过大时，PSF 弥散，系统中存在的像差成分复杂且分布杂乱，将会导致椭率数值计算不精准。为了实现椭率评价指标的尽快融入，应先校正由系统离轴而产生的主要像差。

2）当自由曲面面型项被添加到光阑面时，仅会产生当前所对应的这一种像差类型；当其被添加到非光阑面时，每种类型的Zernike 自由曲面项都可以校正一组特定的像差。

3）借助光学设计软件中的全视场像差分布图作为比较，分析像差节点分布和椭率节点分布的关联性，结合像差理论可以确定每一步需要修改的具体自由曲面项和添加自由曲面项的表面，将椭率关联性较强的像差分量作为优先校正参数进行迭代。

4）若无法找到需要优先校正的像差类型，或添加对应的自由曲面面型后像差校正仍不够完全，则说明当前系统受到结构制约，考虑变换结构参数重新分布系统像差。当大部分像差都校正完毕，系统像差以某一非旋转对称像差为主要成分时，椭率的节点分布接近该像差的节点分布。

如图3 所示，波像差与椭率的融合型优化设计流程为：

图3 波像差与椭率的融合型优化设计流程Fig. 3 Optimization design process for the fusion of wavefront aberration and ellipticity

1）构建三个镜面均为球面的初始结构，优化曲率半径、空气间隔、倾斜量等结构参数得到无遮拦离轴的结构布局。

2）对由系统离轴所引入的像散和彗差进行初步校正，以便PSF 椭率的求解与融入。为了进一步降低波像差，提高PSF 的能量集中度，还需通过圆锥系数项校正旋转对称像差中的球差成分，在全视场波像差RMS 值达到2λ的量级后，椭率的计算可以引入，但由于PSF 过于弥散，椭率的计算尚不够精准。

3）从像差与椭率校正的角度出发，分析需要添加的自由曲面项，优化系数变量获取新结构，并计算全视场的光学椭率分布，将其作为评价指标推入光学设计软件中，赋予适当权重，进行波像差与椭率的联合优化，当全视场波像差RMS 值降低到0.2λ以下时能够获取平缓的全视场椭率分布及精确的椭率数据。

4）在新结构中分析需要优先校正的像差成分或需要变化的结构参数，重复步骤3），迭代更新光学系统结构，逐步降低与椭率关联性较强的非旋转对称像差，最终获得椭率与波像差校正完成的自由曲面结构。

2 离轴三反式自由曲面空间望远镜设计实例

2.1 光学设计指标

同轴系统中主镜的环形孔径、次镜的支撑机构遮挡，均使得同轴系统的孔径函数复杂，影响PSF 的分布。无遮拦离轴光学系统拥有更小且清晰的PSF，无中心遮拦，因而孔径函数为圆形，PSF 仅与像差相关，在椭率性能方面更具先天优势，故采用离轴三反式自由曲面光学系统作为空间望远镜光学系统结构，其指标要求如表1 所示。

表1 光学系统指标要求Table 1 Optical system index requirements

2.2 融合椭率判据的自由曲面面型Zernike 项优化策略

离轴三反光学初始结构的求解通常有两种设计思路［16］：一是先根据初级像差理论求解同轴系统初始结构参数，再通过视场离轴或孔径离轴的方式实现无中心遮拦，但搭建过程较为复杂，初始结构的求取需要进行大量运算，经由反复迭代完成系统离轴，避免光路的遮拦；二是直接构建离轴无遮拦的简单光学系统，在优化过程中利用复杂面型对像差进行优化，避免了繁琐的计算和复杂的离轴迭代，拥有更高的离轴自由度，且系统结构几何空间关系明确。

采用第二种设计思路进行初始结构的设计。为了便于加工装调，选取正-负-正（Positive Negative Positive，PNP）的三反结构。将孔径光阑设置在主镜，三面反射镜均采用球面镜，并使用Zemax 编程语言（Zemax Programming Language，ZPL）离轴结构限制宏确保系统不会出现遮拦问题，经过初步优化后得到的结构参数如表2 所示，初始结构如图4 所示。

表2 光学系统初始结构参数Table 2 Initial structural parameters of optical system

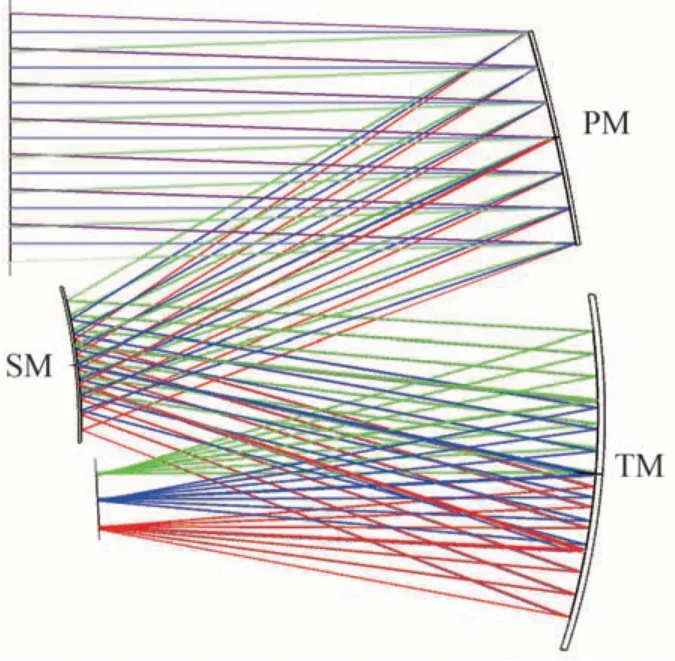
图4 离轴三反望远镜初始结构Fig. 4 Initial structure of off-axis three-reflective telescope

像散和彗差为初始结构的主要像差成分，且这两种非旋转对称像差对椭率影响较大，需优先校正。此时系统成像质量较差，过大的像差将会导致PSF 的弥散与不准确，需要待系统中主要像差进一步降低后计算出精确的PSF 数据。对于像散项来说，无论其被添加的表面是否为为光阑面，都仅会产生像散这一种类型的像差。通过将自由曲面面型像散项设为变量来实现像散的校正。选择在主镜和三镜上添加像散项，校正前全视场像散平均值为7.112 1λ，添加自由曲面面型像散项后平均值降低为0.550 8λ。添加像散项前后的系统全视场像差分布如图5 所示。全视场离焦平均值由0.815 6λ变为3.121 0λ，其最大值由26.852 1λ降低为24.571 1λ。全视场彗差平均值由14.798 0λ降低为14.544 1λ。

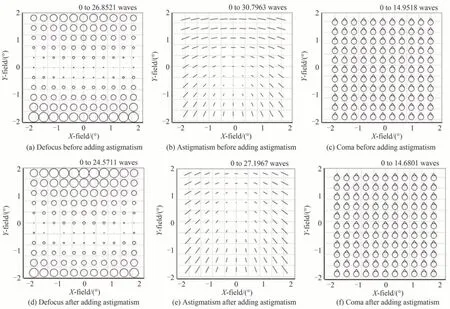
图5 像散添加前后的全视场像差Fig. 5 Full-field aberration before and after adding astigmatism

当前系统的主要像差为离焦和彗差，可以通过在主镜和三镜添加彗差项来校正。在非光阑面添加彗差项会产生三种类型的像差，分别为离焦、像散和彗差。将彗差项添加到表面后的全视场像差如图6 所示，彗差项的添加引入了彗差节点，大幅降低了系统中的彗差分量，全视场彗差平均值由14.544 1λ降低为0.597 6λ。全视场离焦平均值由3.121 0λ降低为1.498 8λ；像散最大值降低超过50%，由27.196 7λ降低为11.277 6λ，平均值由0.550 8λ变为1.200 6λ，全视场分布变得更加平均。

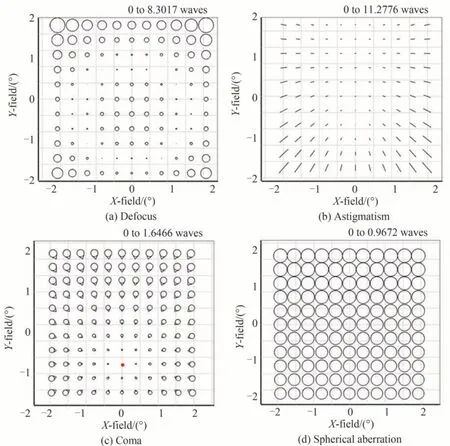
图6 添加彗差后的全视场像差Fig. 6 Full-field aberration after adding coma

此时，系统主要受到旋转对称像差的限制，系统总像差中的非旋转对称成分已经得到了有效降低，在三个反射镜表面添加圆锥系数可以校正旋转对称像差。添加圆锥系数后的全视场像差如图7 所示。其中，全视场离焦平均值由1.498 8λ降低为0.908 7λ，球差平均值由0.884 3λ降低为0.544 4λ。全视场像散平均值降低为0.547 9λ，彗差平均值降低为0.428 6λ。

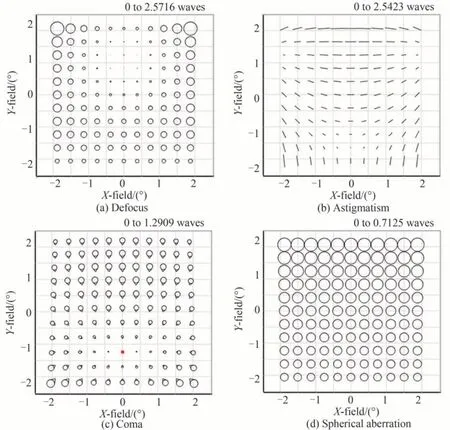
图7 添加圆锥系数后的全视场像差Fig. 7 Full-field aberration after adding conic coefficient

通过旋转对称像差的进一步校正，系统的PSF 能量分布更加集中，全视场波像差RMS 值降低到2λ以下，经由PSF 得到椭率数据，并将其导入到系统评价函数中，赋予适当权重，等待下一次优化。当前系统像差中离焦、像散、彗差、球差都处于同一数量级，为了改变系统中的像差成分并释放设计空间，将反射镜曲率半径、空气间隔和反射镜倾斜作为自由变量，融合椭率指标进行优化，变换结构后系统全视场像差如图8 所示。此时，全视场离焦、像散、彗差及球差的平均值分别为0.016 7λ、0.009 2λ、0.109 7λ和0.000 4λ。

图8 变换结构后的全视场像差Fig. 8 Full-field aberration after structural transformation

随着反射镜的倾斜方向与反射镜上光焦度分布的改变，系统的视场相关性像差，即非旋转对称性像差发生了变化，彗差节点由一个增加到三个，得到了进一步平衡。当前系统中主要像差是三叶形，全视场平均值达到了0.272 9λ。在非光阑面添加三叶形项可以同时校正三叶形和像散。在主镜和三镜添加三叶形项后的全视场像差如图9所示，全视场彗差、三叶形、像散及二次彗差的平均值分别为0.114 6λ、0.039 5λ、0.004 3λ和0.028 2λ。

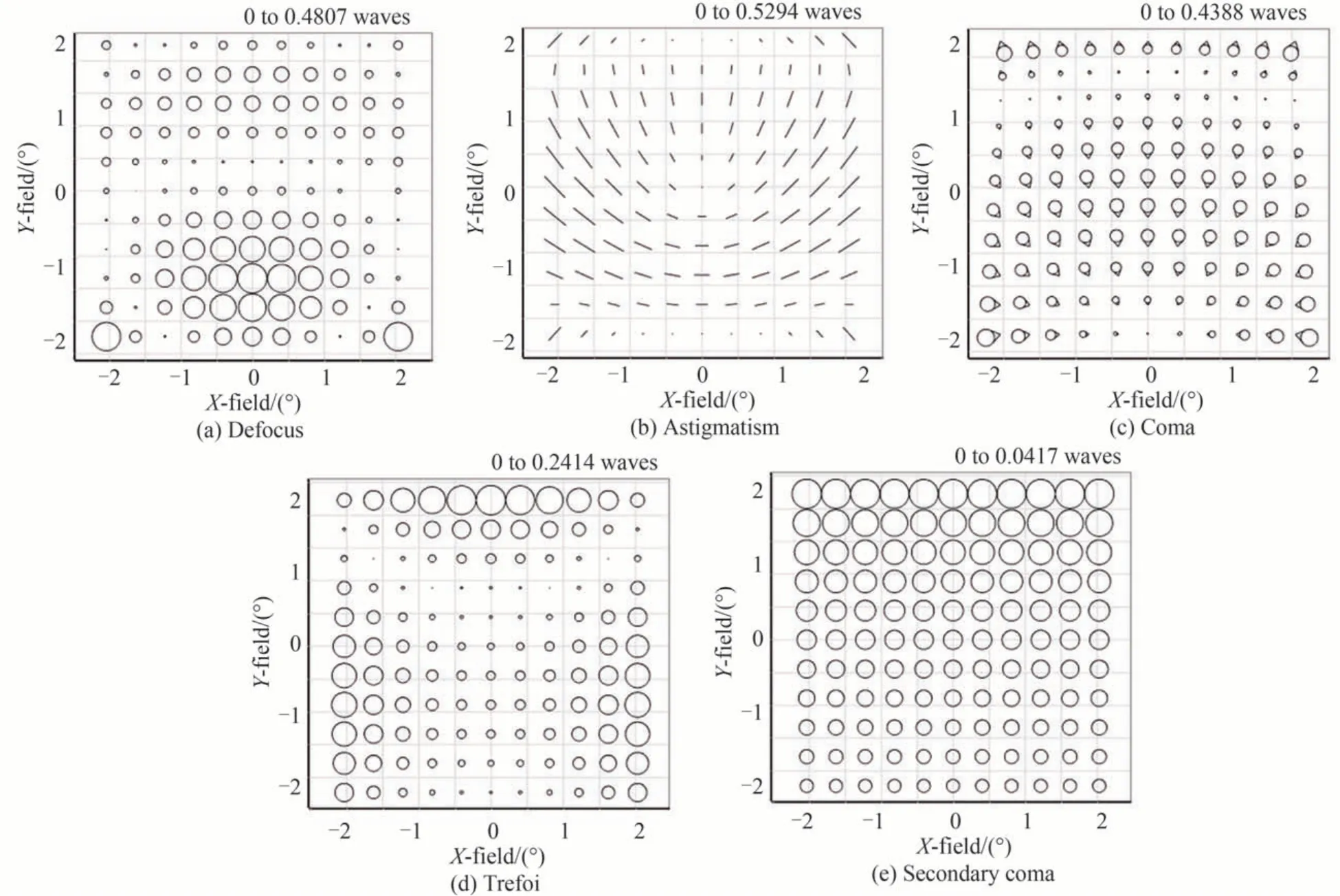
图9 添加三叶形后的全视场像差Fig. 9 Full-field aberration after adding trefoil

本次添加引入了更多三叶形节点，此时需校正的主要像差为彗差，其次是三叶形和二次彗差。在非光阑面添加二次彗差项可以校正七种类型的像差，分别为离焦、像散、彗差、球差、三叶形、二次像散和二次彗差。为了最大化校正像差，在三个反射镜表面都添加了二次彗差项，全视场像差如图10 所示，全视场离焦、像散、彗差、三叶形及二次彗差的平均值分别为0.026 9λ、0.009 8λ、0.005 3λ、0.001 3λ和0.021 2λ。当前全视场波像差RMS 值降低到0.2λ以下，PSF 椭率分布已经足够平缓精确，且与系统波前RMS 分布情况近似，如图11 所示，椭率最大值为0.598 6，平均值为0.328 9。

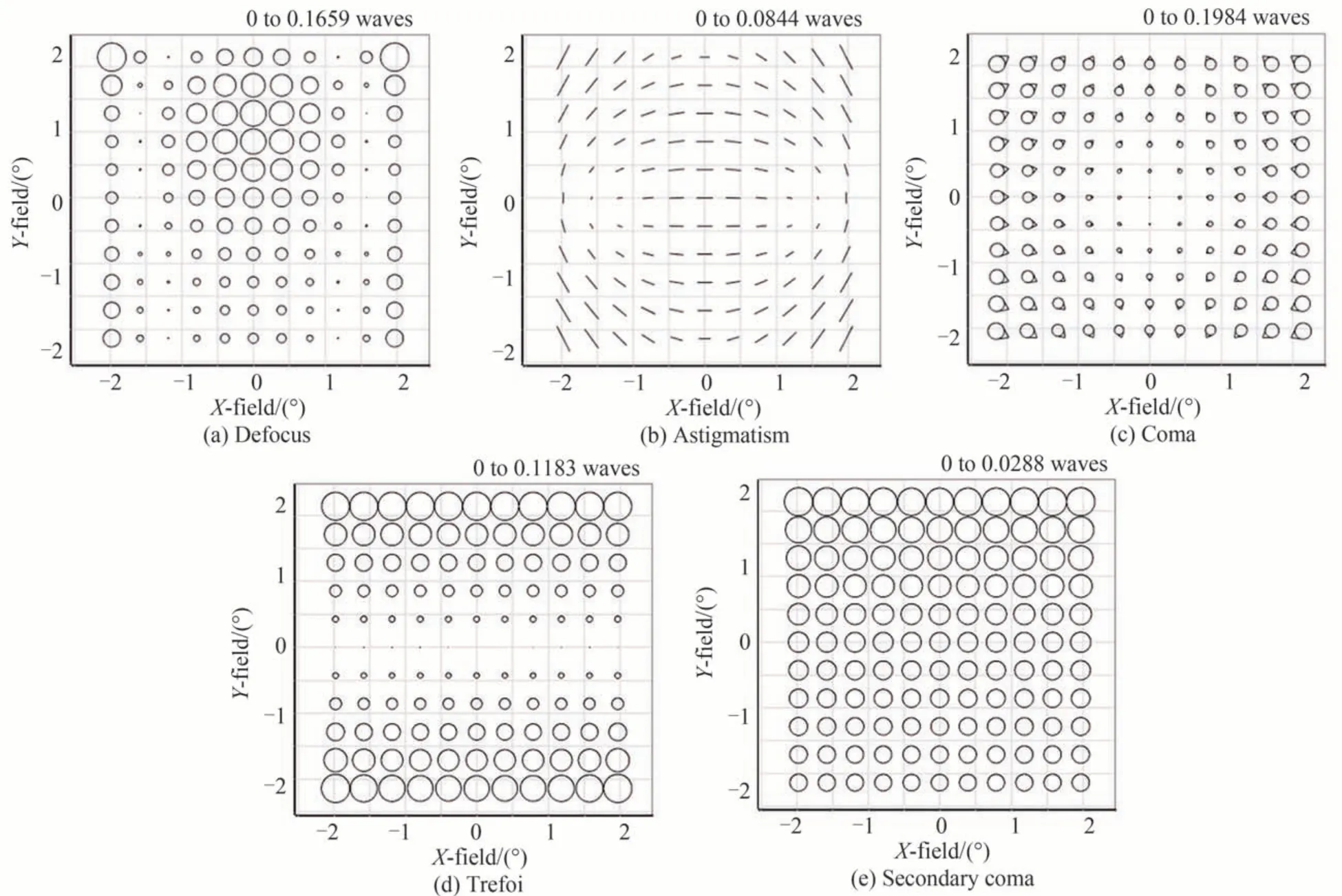
图10 添加二次彗差后的全视场像差Fig. 10 Full-field aberration after adding secondary coma

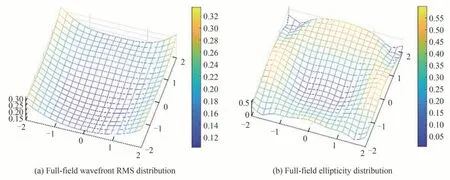
图11 添加二次彗差后的波前RMS 分布与椭率分布Fig. 11 Wavefront RMS distribution and ellipticity distribution after adding secondary coma

现在系统主要受到离焦、像散、二次彗差的限制。二次彗差在已经校正过的情况下较其他类型像差相比仍大了一个数量级，通过再次变换结构来改变系统离轴像差的分布，结构优化后的全视场像差、波前RMS分布和PSF 椭率分布如图12 和13 所示，全视场离焦、像散、彗差、二次像散及二次彗差的平均值分别为0.000 1λ、0.019 4λ、0.004 0λ、0.027 1λ和0.002 6λ，椭率最大值为0.300 8，平均值为0.114 6。

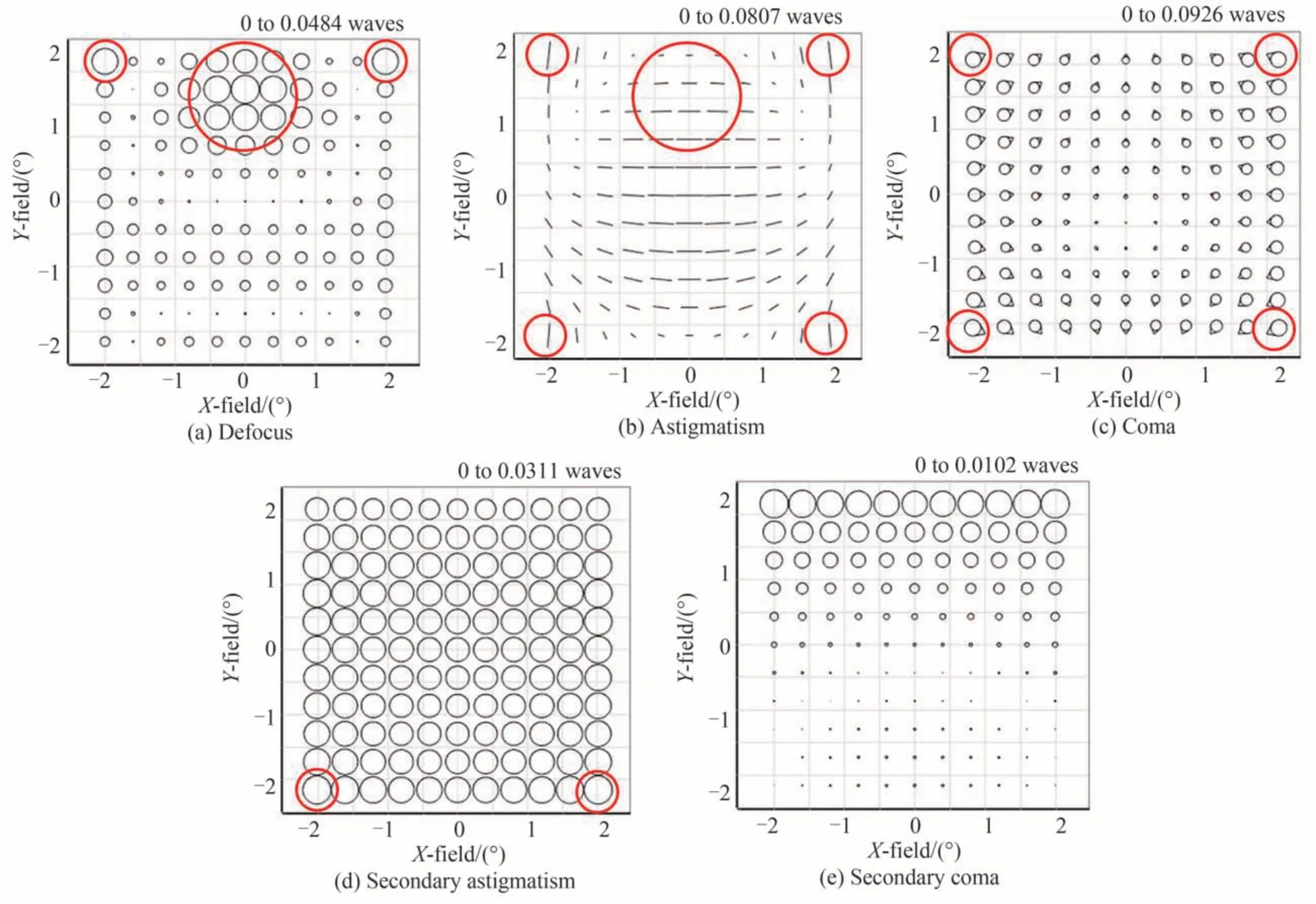
图12 变换结构后的全视场像差Fig. 12 Full-field aberration after structural transformation

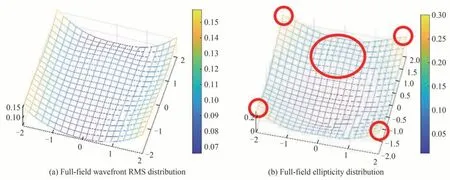
图13 变换结构后的波前RMS 分布与椭率分布Fig. 13 Wavefront RMS distribution and ellipticity distribution after structural transformation

当像散和离焦同时存在时，离焦会使得PSF 椭率进一步增大。通过PSF 椭率凸点分布及全视场离焦分布可以看出，影响椭率和波前分布的主要像差为像散和二次像散。在非光阑面添加二次像散项可校正离焦、像散、彗差、三叶形和二次像散共五种类型的像差，综合考虑波像差及椭率的优化效果后选择在三个反射镜表面都添加二次像散项，得到的系统全视场像差、波前RMS 分布和PSF 椭率分布如图14 和15 所示，全视场离焦、像散、彗差及二次像散的平均值分别为0.005 3λ、0.008 5λ、0.000 2λ和0.000 2λ，椭率最大值为0.046 4，平均值为0.014 7。

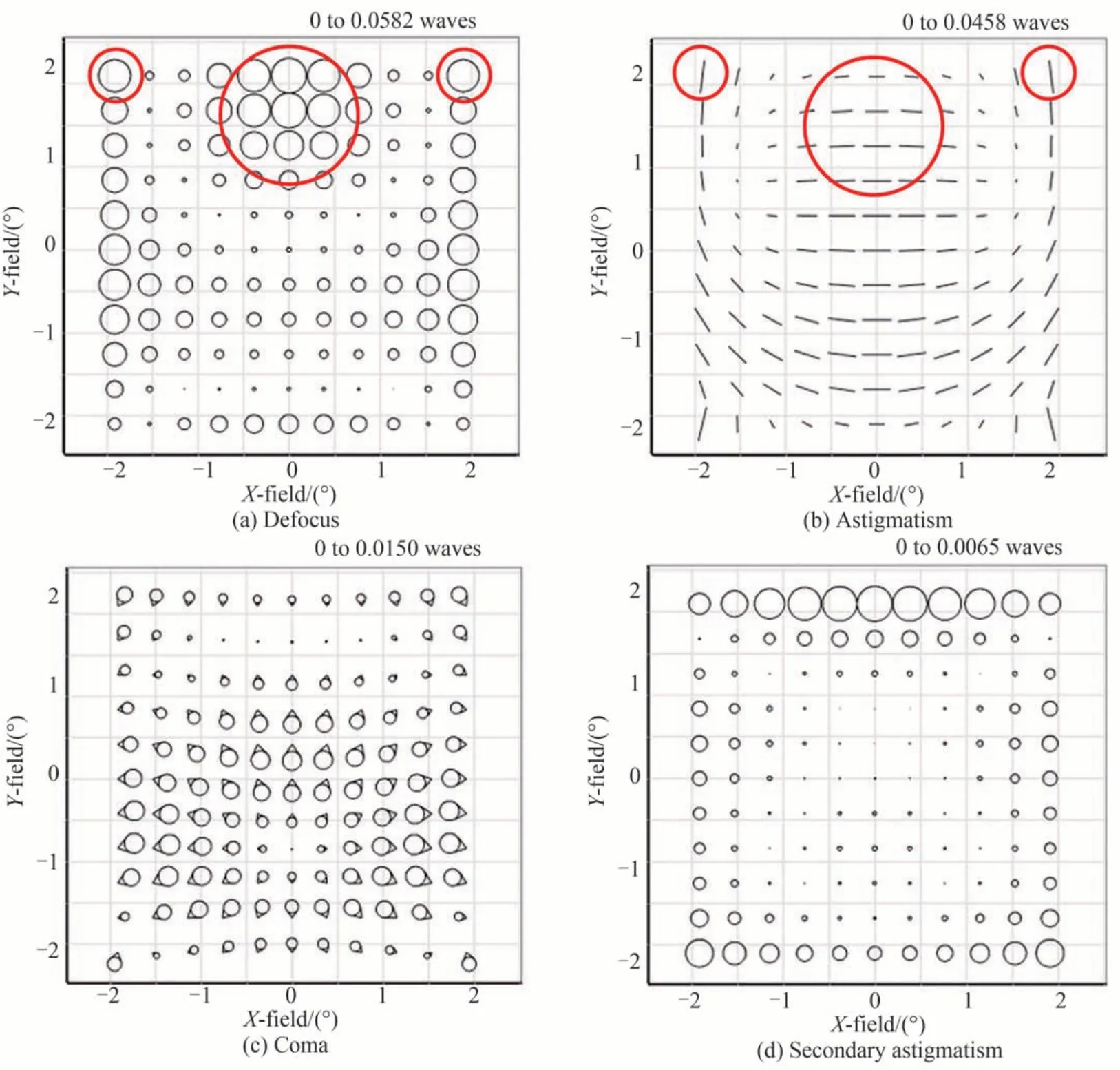
图14 添加二次像散后的全视场像差Fig. 14 Full-field aberration after adding secondary astigmatism

图15 添加二次像散后的波前RMS 分布与椭率分布Fig. 15 Wavefront RMS distribution and ellipticity distribution after adding secondary astigmatism

需要添加的自由曲面Zernike 项添加完毕，最后变换一次结构重新平衡像差后，得到的系统全视场像差、波前RMS 分布和PSF 椭率分布如图16 和17 所示，此时的椭率最大值及平均值均已降低到光学系统指标要求以下，系统成像质量良好，全视场离焦、像散、彗差、三叶形、二次像散及二次彗差的平均值分别为0.001 4λ、0.002 4λ、0.002 5λ、0.002 0λ、0.000 9λ和0.000 7λ，椭率最大值为0.030 3，平均值为0.015 6。

图17 最终结构的波前RMS 分布与椭率分布Fig. 17 Wavefront RMS distribution and ellipticity distribution of the final structure

本次优化过程中Zernike 像差随优化步骤变化折线如图18 所示。

图18 Zernike 像差随优化步骤变化折线Fig. 18 Line chart of Zernike aberration changes with optimization steps

2.3 优化结果

采用椭率关联性较强的像差分量优先校正的自由曲面面型Zernike 项优化方法，望远镜系统三面反射镜自由曲面面型仅采用Z5、Z8、Z11、Z12 和Z15 项Zernike Fringe 多项式进行表征，最终系统结构参数及自由曲面各项系数如表3 和4 所示，波像差RMS 平均值为0.035 2λ，接近衍射极限，光学系统像质良好，椭率最大值为0.030 3，平均值为0.015 6。

表3 本文方法优化结果结构参数Table 3 Structural parameters of the optimization result of the proposed method

表4 本文方法优化结果Zernike Fringe 多项式项系数Table 4 Zernike Fringe polynomial coefficients of the optimization result of the proposed method

传统优化方法首先通过优化conic 系数将球面转化为圆锥曲面，然后在其基础上按照从低阶项到高阶项的顺序在所有镜面添加自由曲面面型Zernike 项来校正像差，且在添加过程中持续保持系统结构参数变量可变化。传统优化结果的各子镜面形参数如表5 所示，三个镜面的自由曲面面形矢高比对如图19 所示。传统优化结果的波前RMS 分布与椭率分布如图20 所示，波像差和椭率的全视场均值差异较小。但与从低阶项到高阶项的传统像差校正优化方法相比，采用本方法设计的自由曲面望远镜自由曲面偏差相对更小。其中，次镜的区别最大，本文方法在次镜上仅添加Z12、Z15 项，而传统优化方法在三个镜面均添加了全部5 种Zernike 项，次镜产生的自由曲面矢高是本文方法的25 倍，像散项和彗差项存在设计冗余，无添加的必要性。两种方法优化结果对比如表6 所示，通过对像差节点的调控，采用本方法优化所得到结果的成像质量和椭率性能都得到了同步控制，椭率最大值被进一步压缩，椭率分布更加均衡。

表5 传统优化结果Zernike Fringe 多项式项系数Table 5 Zernike Fringe polynomial coefficients of the traditional optimization result

表6 不同方法优化结果对比Table 6 Comparison of optimization results using different methods

图19 本文方法优化结果与传统优化结果的自由曲面偏差Fig. 19 The deviation of freeform surface between the proposed method and traditional optimization results

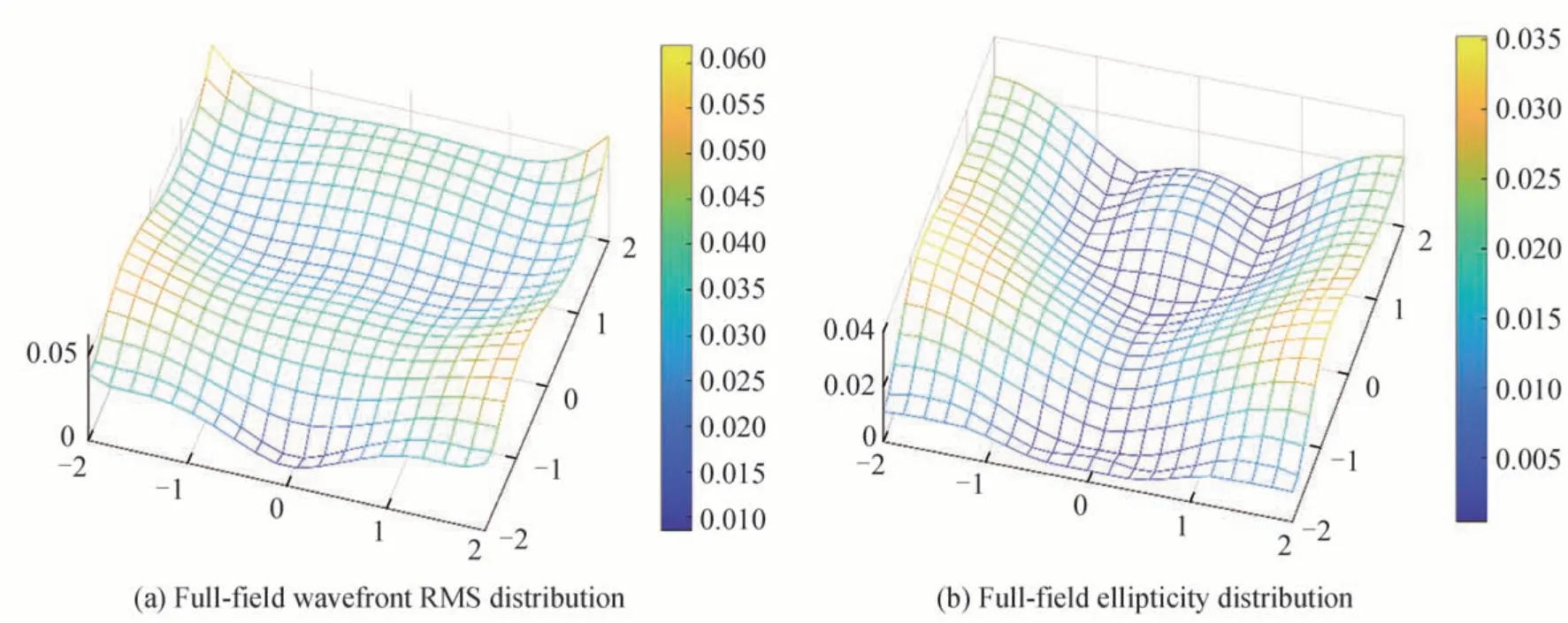
图20 传统优化结果的波前RMS 分布与椭率分布Fig. 20 Wavefront RMS distribution and ellipticity distribution of the traditional optimization result

3 结论

本文以焦距为600 mm，口径为200 mm，视场为4°×4°的离轴三反自由曲面望远镜系统为设计需求样例，完整描述了将光学椭率指标融入到设计的正向过程的方法。应用椭率关联性较强的像差分量优先校正的自由曲面面型Zernike 项优化方法对初始结构进行了波像差和椭率的联合优化设计，与从低阶项到高阶项的传统像差校正优化方法得到的结果相比，采用本方法设计的自由曲面望远镜系统采用了相对较小的自由曲面偏差，在像质和椭率性能方面得到了同步控制，充分发挥了自由曲面的效能，更具优化设计的效率优势。