基于PROA-BP 的激光3D 投影振镜偏转电压预测模型

林雪竹，王海，郭丽丽，闫东明，李丽娟，刘悦，孙静

（1 长春理工大学 光电工程学院 光电测控与光信息传输技术教育部重点实验室，长春 130022） （2 长春理工大学中山研究院，中山 528437）

0 引言

激光3D 投影技术是一种高精度的投影技术，其原理是利用激光光束照射到工件上，并通过激光光束的三维扫描来实现对工件表面图案的投影，该技术的核心功能为双轴扫描振镜系统。这种技术具有高精度、高效率和高稳定性等优点，在复合材料铺贴、零部件辅助装配、汽车装配和航空航天等领域得到广泛应用［1-2］。

激光3D 投影系统的振镜偏转电压预测精度对投影精度直接影响，激光3D 投影系统的振镜偏转电压预测精度主要取决于外部参数（投影系统与被投影工件相对位置）以及双轴扫描振镜系统内部参数的标定精度［3］，该系统内部参数与外部参数高精度标定才能实现高精度投影。激光3D 投影系统外部参数标定通常采用牛顿迭代法［4］、最小二乘法［5］、粒子群优化算法［6］等解算投影机与工件相对位置关系，但算法解算精度易受双轴扫描振镜系统内部参数振镜偏转角与两转轴公垂线e误差影响，容易陷入局部最优解。激光3D 投影系统的双轴扫描振镜系统的内部参数标定主要是对振镜偏转电压(u，v)与转轴实际偏转角(H，V)之间的比例系数(k1，k2)和两转轴公垂线长度e标定［7］。近年来，激光投影系统的振镜偏转电压预测不仅仅局限于原理性误差和外部误差的补偿，还对激光3D 投影模型进行优化与研究来提高预测精度。MANAKOV A 等［8］在理想模型的基础上考虑入射光方向以及激光器位置两个因素，建立了一个更符合实际情况的复杂模型，引入更多振镜系统内部参数，采用全局优化的方法求解内外共12 个参数，大大提高了振镜偏转电压的预测精度，但此模型标定过程繁琐且求解时间长，优化结果容易陷入局部最优解。刘邈等［9］提出用双目视觉测量系统辅助标定振镜偏转电压(u，v)与两轴实际转角之间的比例系数(k1，k2)和两转轴公垂线长度e，采用近似模型法和查表法构建激光3D 投影传统模型与矢量模型，提高激光3D 投影系统内参标定精度，预测振镜偏转电压更加准确。但由于比例系数(k1，k2)采用线性拟合获得，拟合精度易受投影系统综合非线性误差影响，导致投影定位精度损失。

针对激光3D 投影系统的综合非线性误差带来的投影定位精度损失问题，本文提出一种基于改进的鱼优化算法-BP 神经网络（Poisson Remora Optimization Algorithm- Back Propagation， PROA-BP）的激光3D 投影振镜偏转电压预测模型，实现对所需投影位置振镜偏转电压精准预测。PROA 用于解决神经网络易陷入过拟合问题，BP 神经网络通过神经网络多层结构和非线性激活函数，在大量实验数据的基础上，建立激光出射方向单位矢量与振镜偏转电压(u，v)非线性映射关系的预测模型，耦合与补偿激光3D 投影系统非线性误差，实现激光3D 投影系统的高精度投影。最后，将此模型与传统模型进行投影仿真对比，分析投影定位精度，并通过实验验证模型可行性。

1 激光3D 投影系统传统数学模型

现有的激光3D 投影系统数学模型，主要是针对二维振镜偏转水平角V和俯仰角H与投影目标点坐标建立的数学模型。为实现投影图形精确投影需获得投影图形在投影系统坐标系下的空间位置信息，因此需先建立激光投影坐标系，确定所需投影图形在投影坐标系下的空间位置，通过二维振镜快速扫描技术实现投影图形投影。投影坐标系定义为：X轴振镜中心为激光投影坐标系原点O；以X轴振镜的转轴方向作为激光投影坐标系正X轴方向；以Y轴振镜中心与X轴振镜中心的连线方向为激光投影坐标系的正Y轴；根据右手定则确定激光投影坐标系Z轴正方向。

激光投影系统的内部几何关系结构如图1 所示。在理论的状态下，激光器发出激光束出射到Y轴振镜上发生偏转反射，反射的激光束再入射到X轴振镜上发生偏转反射射出，最终激光束投影到目标工件上。如图1所示，e为X轴振镜中心与Y轴振镜中心间距，激光束偏转角分别为水平角H和俯仰角V。设CD=d，则投影目标点P在投影坐标系的坐标可由d、e、V、H表示，根据几何关系可得到P在投影坐标系的坐标表示

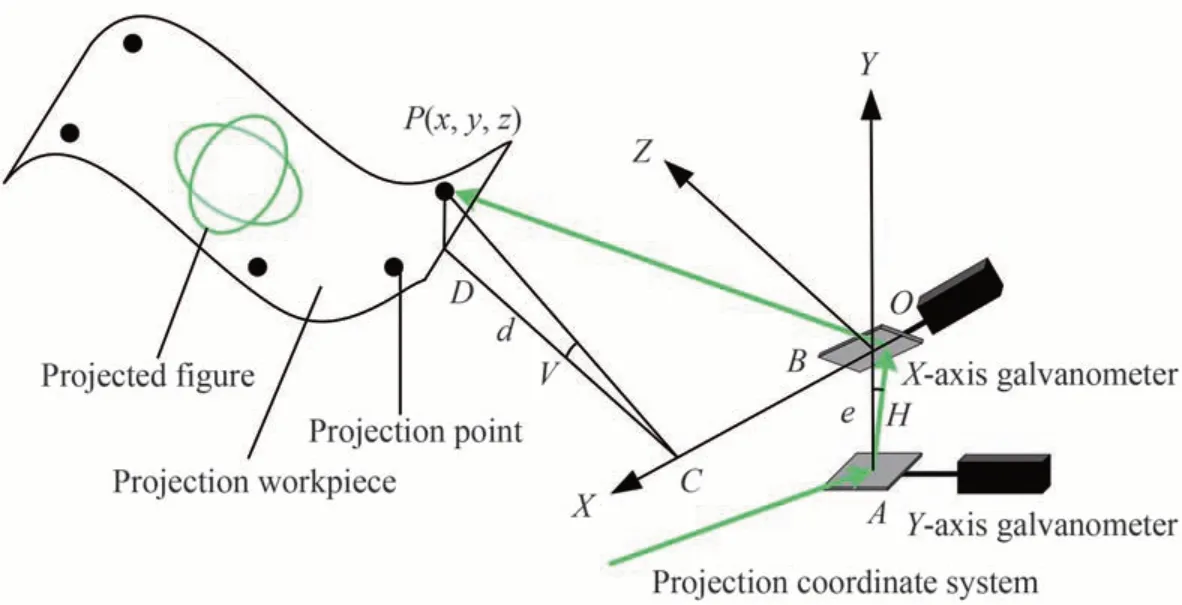
图1 激光投影系统内部几何关系Fig.1 Laser projection system internal geometric relationship structure diagram

振镜偏转角H、V和P点坐标值关系为

传统模型通过线性拟合标定振镜偏转电压(u，v)与两转轴实际转角之间的比例系数(k1，k2)，振镜偏转电压为

此模型精度易受振镜偏转角偏差和内参e标定精度影响，其投影过程中存在大量非线性误差。

2 基于PROA 算法优化的BP 神经网络

2.1 BP 神经网络

BP 神经网络是一种常见的神经网络，也称为多层感知器（Multilayer Perceptron， MLP），具有强大的非线性建模能力，对未知的输入数据具有很好的推广能力，能够较好的预测。BP 神经网络结构与神经元结构如图2 所示，输入层接收需要处理的数据并导入，隐含层对导入数据运算处理，输出层输出结果。BP 神经网络通过反向传播不断迭代每个神经元的权重与偏置，提高网络准确率。但其运用在较复杂问题时，需要大量的计算资源和数据来训练模型，容易陷入局部最优解或产生过拟合现象，效率低下［10］。

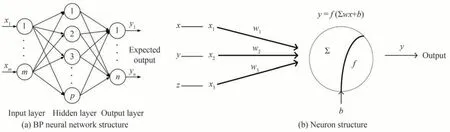
图2 BP 神经网络结构与神经元结构Fig.2 BP neural network structure and neuron structure

2.2 PROA 算法

为解决BP 神经网络容易陷入局部最优解问题，将改进的ROA 算法（PROA）与BP 神经网络相结合，优化神经网络初始权重与偏置。原始鮣鱼优化算法（Remora Optimization Algorithm，ROA）主要模拟了鮣鱼的寄生特性完成优化过程的［11］，先根据初始化种群位置计算个体适应度，得到当前最优位置和最优适应度。通过寄生鲸鱼与旗鱼，使用鲸鱼优化算法（Whale Optimization Algorithm， WOA）策略或旗鱼优化算法（Sailed Fish Optimizer， SFO）策略更新位置寻找最优解。WOA 策略公式为

SFO 策略为

当吸附于宿主身上时，在宿主周围进行小范围移动进行局部搜索，会根据上一代鱼的位置与当前宿主的位置，判断是否需要更换宿主，其公式为

式中，Ratt为尝试的新位置，为第t次迭代过程中的第i个个体，Rpre为上一个历史位置，当更新位置的适应度小于原始位置适应度时，更换寄主。

改进的鮣鱼优化算法中对局部搜索引入了类泊松随机策略得到式（10）。

改进的鮣鱼优化算法使用3 种增强随机策略代替原有的SFO 策略，表示为

2.3 PROA-BP 神经网络

PROA-BP 神经网络算法流程如图3 所示，具体步骤为：1）根据实验数据需要构建激光出射方向单位矢量和振镜偏转电压的数据集，并对数据进行归一化处理；2）将数据导入搭建的PROA-BP 神经网络，对BP神经网络初始化和PROA 种群初始化；3）PROA 根据BP 神经网络建立对应适应度函数，计算当前适应度来寻找个体以及全局的最优解；4）通过全局勘探和局部搜索实现位置更新，找到满足最大迭代次数或预设误差精度的最优权值与偏置；5）将PROA 得到的最优权值与偏置赋予BP 神经网络，进行迭代训练，直至网络损失稳定，将模型保存；6）调用模型，输入投影点坐标相对于原点单位方向矢量，预测振镜偏转电压值，并输入至激光3D 投影系统进行投影定位。

图3 利用PROA-BP 神经网络预测振镜偏转电压流程Fig.3 Use PROA-BP neural network predictive galvanometer deflection voltage process

3 基于PROA-BP 的预测模型构建

3.1 实验数据获取与处理

由模型构造要求所知，实验数据需要投影机激光出射方向单位矢量与振镜偏转电压(u，v)的对应数据。为获取实验数据，需先借助双目相机测量系统建立投影坐标系，其建立过程如图4 所示。令出射激光束固定，多次移动标定板位置，通过相机测得激光束在不同空间位置标定板上的坐标，将这些点以最小二乘法拟合直线可得到激光束在相机坐标系下的直线方程。

图4 投影坐标系建立Fig.4 Projection coordinate system

当两转轴均设置为0 度时，令激光出射直线方向为正Z方向。保持转轴2 为0 度，控制振镜偏转电压转动转轴1，多次移动标定板位置，相机测量转轴1 不同角度时激光束在标定板上的点，将测得所有点拟合平面，该平面的法向方向定义为Y轴，X轴方向依据右手定则定义。控制转轴1 为零度，控制振镜偏转电压转动转轴2，相机测量转轴2 不同角度时激光束在标定板上的点，每个激光束拟合出直线方程。这些直线与前一步拟合平面相交，得到转轴2 不同角度的激光直线与拟合平面的交点，交点的平均值定义为原点，至此投影坐标系建立完成。

如图5 所示，通过输入不同的(u，v)，使得两转轴偏转，激光束投射在标定板上，双目相机测得不同(u，v)对应的投影点坐标。因投影坐标系是在相机坐标系下建立的，两坐标系下相对位置关系已知，可将双目相机坐标系下的激光点坐标转换到投影坐标系下的投影点坐标，即可求出投影点坐标对应的激光出射方向单位矢量，最终得到激光出射方向单位矢量与振镜偏转电压(u，v)对应的1 681 条实验数据，将这些数据根据8∶2 分为训练集与验证集。

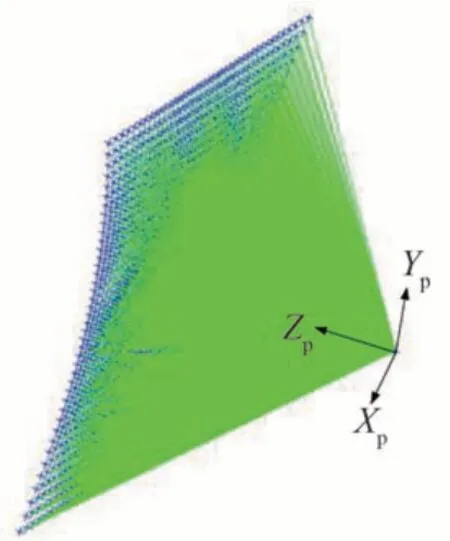
图5 数据集获取Fig.5 Dataset acquisition

3.2 神经网络参数确定

3.2.1 模型评价指标

为评价模型的预测效果，使用均方根误差（Mean Square Error， MSE）和平均绝对误差（Mean Absolute Error， MAE）来评价神经网络预测模型的性能［12-13］。计算公式分别为

3.2.2 BP 神经网络结构。

BP 神经网络的关键在于网络构造，包含网络层数和结点数量的选定。网络结构包含输入层、隐含层和输出层3 层。输入层与隐含层间选用双曲正切函数Tanh 作为传递函数，隐含层与输出层间的选取线性函数Purelin 作为传递函数。由于Hecht-Nielson 在理论上已经证明一个隐含层的BP 神经网络能够逼近任何区间内的连续函数［14］，因此选用一个隐含层的结构。BP 神经网络隐含层的神经元个数取值依据式（18）初步确定为3～13 个，不同神经元个数的MSE 与MAE 如图6 所示，根据MSE 与MAE 的误差大小，最终确定神经元数为：输入层3 个、隐含层12 个、输出层2 个，学习率为0.000 1。

图6 不同神经元个数下的MSE 和MAEFig.6 MSE and MAE under the number of different neurons

式中，p为隐含层神经元数量；m为输入参数数量；n为输出参数数量；A为［1，10］之间的常数。

3.3 PROA 参数确定

PROA 优化算法中的初始化种群规模对系统的收敛速度、准确性和稳定性都有影响。增加种群规模可以提高算法的搜索精度，但会减慢算法的收敛时间。PROA 种群规模个数为BP 神经网络连接权重与偏置之和，本文为87。根据仿真实验，MSE 值在超10 000 后趋于稳定，所以本文选取PROA 算法参数为种群规模个数87、迭代次数10 000 次。

3.4 PROA-BP 神经网络训练与预测结果

分别对BP 神经网络、粒子群算法-BP（Particle Swarm Optimization Algorithm-Back Propagation， PSO-BP）神经网络和PROA-BP 神经网络通过数据集的训练集进行训练，三种网络训练的MSE 和MAE 如图7所示。

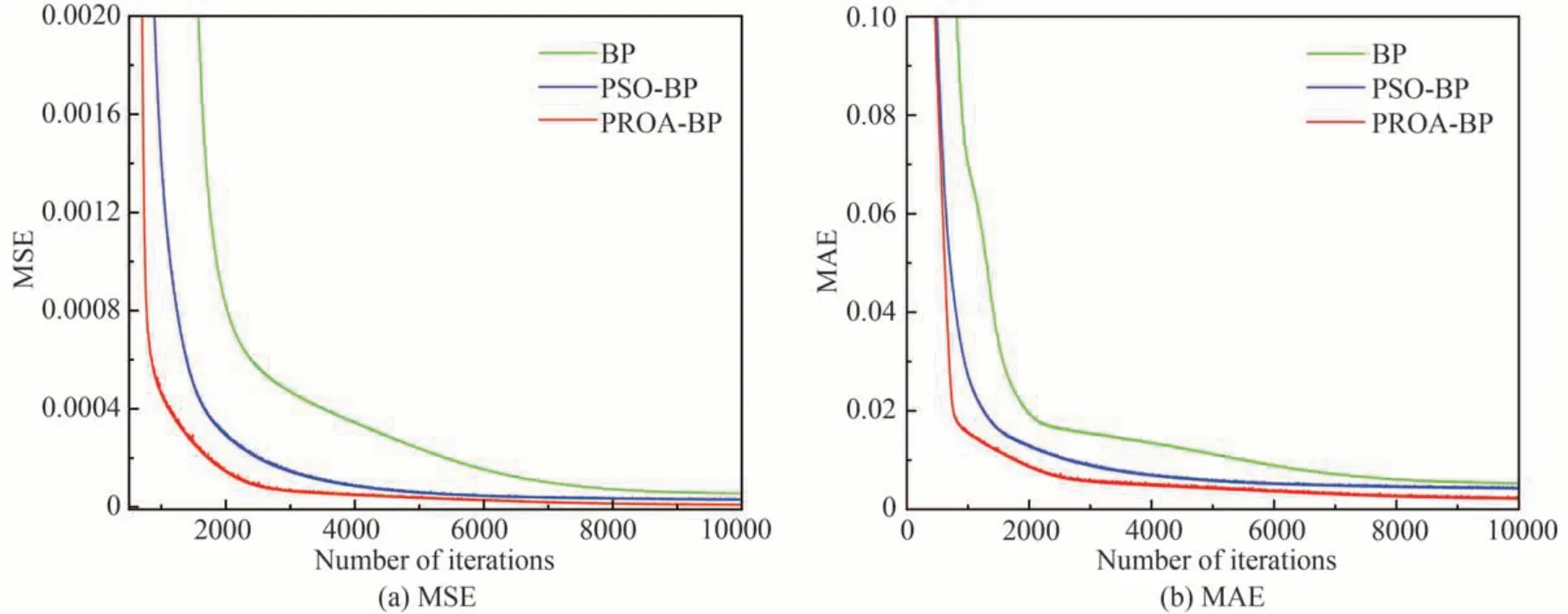
图7 训练集下不同网络结构的MSE 和MAEFig.7 MSE and MAE of different network structures under training dataset

由图7 可知，三个网络各训练10 000 次后，趋于平稳。PROA-BP 神经网络的MSE 和MAE 均值分别是PSO-BP 神经网络的41.2%、62.4%，为BP 神经网络的22.2%、50.7%。PROA-BP 神经网络损失相较于BP和PSO-BP 网络在训练过程中下降的更快，MSE 与MAE 更小。

分别对三种网络已训练好的模型进行验证集的预测，三种网络的振镜偏转电压预测值与实际值的误差绝对值如图8 所示，由图8 可知，相对于BP 网络与BPPSO 网络，PROA-BP 神经网络的预测值与实际值误差更小，振镜偏转电压的预测值与实际值基本保持一致，预测误差基本小于0.003。

图8 不同网络结构的预测误差Fig.8 Prediction errors of different network structures

综上所述，相较于BP 神经网络和PSO-BP 神经网络，PROA-BP 神经网络在预测精度和泛化能力方面表现更为优秀。具体而言，PROA-BP 神经网络在激光3D投影振镜偏转电压预测上能够实现更低的预测误差，使得激光3D 投影系统拥有更高的投影定位精度。

4 仿真与对比分析

4.1 激光3D 投影传统模型投影仿真

激光3D 投影传统模型投影仿真分为理论投影点数据获取、标定投影点数据获取、激光3D 投影传统模型内参标定与激光3D 投影传统模型投影定位精度分析。

根据激光3D 投影传统模型的仿真实验需要，首先获取理论投影点数据。固定传统模型内参k1=6、k2=6、e=6.8，取振镜偏转电压u、v范围为±5V，即振镜偏转角±30°。根据双目视觉测量系统测量范围与测量精度要求，令投影平面z值为1 000 mm，即d=1 000。振镜偏转电压u、v每隔0.25 V 将激光束投影到投影平面上，即V、H每隔1.5°将激光束投影到投影平面上，将对应的V、H与d带入传统模型中的，最终得到1 681 个理论投影点数据。

因二维振镜扫描系统存在振镜偏转角误差，根据系统误差范围，对1 681个理论投影点数据对应的振镜偏转角V、H值施加服从正态分布的均值为0，标准差σ=8″的随机偏转角误差，并将添加完随机误差的振镜偏转角V、H带入传统模型中的，得到施加振镜偏转角误差的1 681个投影点数据。因双目视觉测量系统存在测量误差，对施加振镜偏转角误差的1 681个投影点数据坐标值x、y施加服从正态分布的均值为0，标准差为σ=0.02的随机测量误差，得到含有振镜偏转角误差与双目视觉测量误差的1 681个投影点数据，并定义其标定投影点数据。

通过u=0 时的标定投影点数据对传统模型内参振镜偏转电压v与实际转轴偏转角H的比例系数k2进行标定，令u=0，v=0 时的激光束V、H角度为0°。标定如图9 所示。

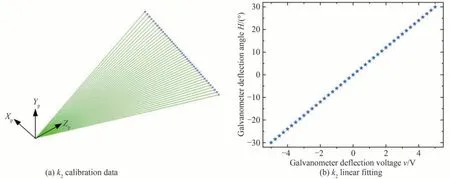
图9 k2 标定Fig.9 k2 calibration

拟合直线得到系数k2=6.004 10。通过v=0 时的标定投影点数据对传统模型内参振镜偏转电压u与实际转轴偏转角V的比例系数k1进行标定，k1标定如图10 所示。

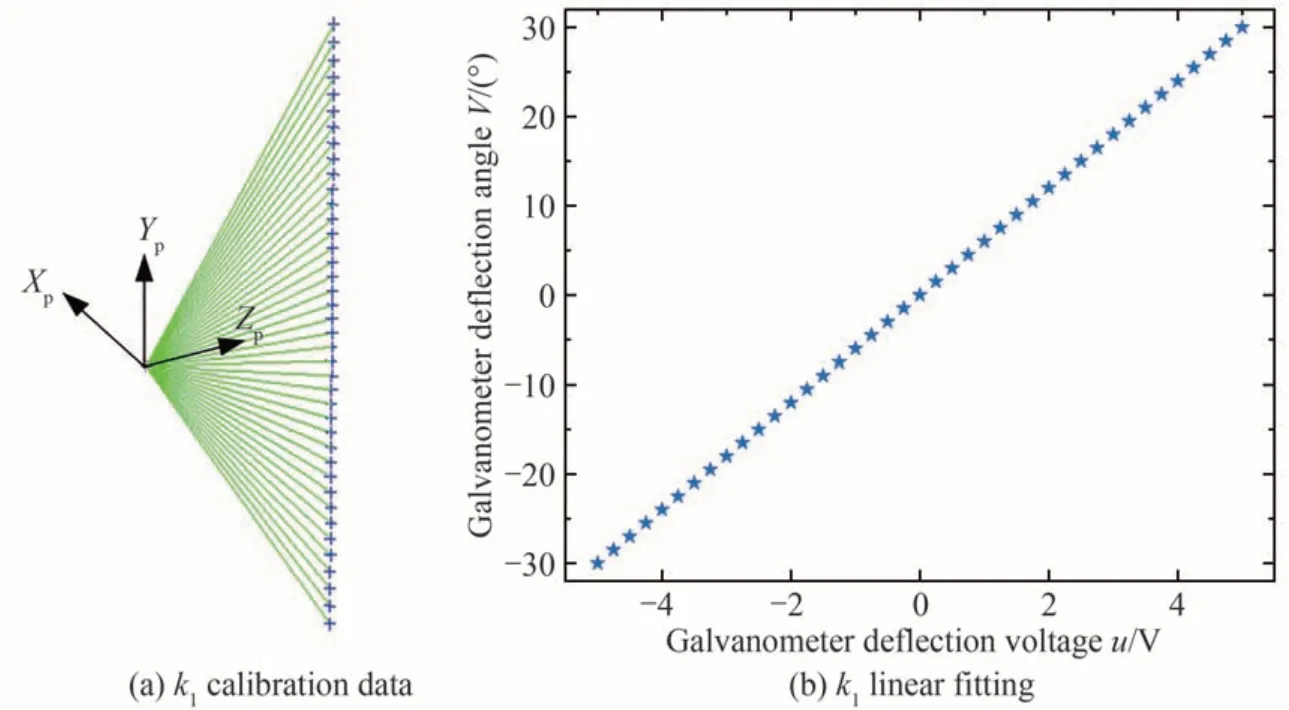
图10 k1 标定Fig.10 k1 calibration

拟合直线得到系数k1=5.999 99。根据式（19），通过带入1 681 个标定投影点数据，得到不同u、v下的e值，通过取均值方式得到e=6.798 37。

激光3D 投影系统传统模型内参已经标定完成，根据已标定完的内参k1=5.999 99、k2=6.004 10、e=6.798 37 进行投影定位实验。令振镜偏转电压u、v每隔0.25 V 将激光束投影到投影平面上，即根据k1=5.999 99 和k2=6.004 10 求出对应电压的振镜偏转角H、V，并将其对应H、V和d带入e=6.798 37 的激光3D 投影传统模型中，获得标定后的激光3D 投影传统模型投影1 681 个实际投影点数据。激光3D 投影传统模型投影仿真部分数据如表1 所示。

表1 激光3D 投影传统模型投影仿真部分数据Table 1 Laser 3D projection traditional model projection simulation part of the data

对比理论投影点数据与实际投影点数据可知，由于振镜偏转角误差和转轴公垂线长度e影响，相同电压下，振镜偏转角误差与公垂线e误差导致投影定位误差，反推可得，振镜偏转角相同，激光3D 投影系统传统模型根据振镜偏转角反推出的振镜偏转电压存在误差，最终导致投影定位误差。令对应投影点坐标之间的欧式距离作为投影定位误差，如图11 所示，激光3D投影传统模型投影仿真中的1 681 个投影点最大投影定位误差约为0.5 mm。

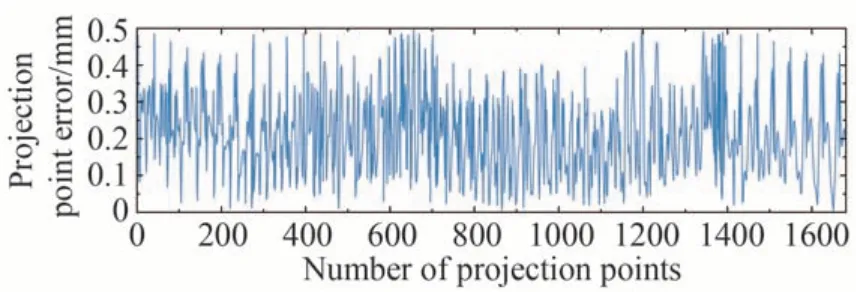
图11 激光3D 投影传统模型投影仿真的投影定位误差Fig.11 Projection positioning error of laser 3D projection traditional model projection simulation

4.2 基于PROA-BP 的激光3D 投影振镜偏转电压预测模型投影仿真

由第3 节可得已训练好PROA-BP 的激光3D 投影振镜偏转电压预测模型。根据双目相机测量精度与范围要求，投影点位置设置于投影坐标系Z轴正前方1 000 mm 处，即令投影平面z值为1 000 mm，d=1 000。

在激光3D 投影系统可投影范围内，在投影平面（d=1 000）上随机选取1 200 个投影点，并与投影坐标系原点解算投影点的对应激光出射方向单位矢量，将其输入到基于PROA-BP 的激光3D 投影振镜偏转电压预测模型中预测出对应的振镜偏转电压，将对应的振镜偏转电压输入到内参k1=6、k2=6、e=6.8 激光3D 投影传统模型中，进行投影验证。基于PROA-BP 的激光3D 投影振镜偏转电压预测模型投影仿真部分数据如表2 所示。

表2 基于PROA-BP 的激光3D 投影振镜偏转电压预测模型投影仿真部分数据Table 2 Projection simulation part of the data of galvanometer deflection voltage prediction model of laser 3D projection based on PROA-BP

计算理论振镜偏转电压与预测振镜偏转电压的激光束投射在投影平面上的投影点坐标之间欧式距离，并令其作为投影定位误差。由图12 可知其投影定位误差最大约为0.35 mm。

图12 基于PROA-BP 的激光3D 投影振镜偏转电压预测模型投影仿真的投影定位误差Fig.12 Projection positioning error of projection simulation based on galvanometer deflection voltage prediction model of laser 3D projection based on PROA-BP

4.3 对比与分析

由两种模型仿真结果可得，激光3D 投影传统模型投影定位误差最大约为0.5 mm，基于PROA-BP 的激光3D 投影振镜偏转电压预测模型投影定位误差最大约为0.35 mm。对比两种模型投影定位误差，结果表明，相较于激光3D 投影传统模型，基于PROA-BP 的激光3D 投影振镜偏转电压预测模型预测能够更好耦合与补偿激光3D 投影系统振镜偏转角偏差与根据振镜偏转角标定的转轴公垂线长度e误差引起的投影系统综合非线性误差，且预测的振镜偏转电压更加精准，投影定位精度更高。

5 实验验证

为验证基于PROA-BP 的激光3D 投影振镜偏转电压预测模型的投影定位精度，搭建由激光3D 投影机、双目相机测量系统、双经纬仪测量系统［15］与标定板等仪器组成的实验验证平台，实验验证平台示意图如图13 所示。在投影机正前方1 000 mm 距离处放置标定板，由3.1 节可知，基于双目相机测量系统构建激光3D 投影机投影坐标系与神经网络数据集，并通过此数据集对PROA-BP 神经网络进行训练，待神经网络损失趋于平稳后保存模型。

图13 实验验证平台Fig.13 Experimental verification platform

标定板上有6 个固定靶座，将反光半球放置固定靶座，并在标定板上均匀的贴500 个反光点，使用双目相机测量标定板上反光点与反光半球，获得反光点圆心与反光半球圆心在双目相机坐标系下三坐标数据。将固定靶座上反光半球换成十字叉丝半球，通过双经纬仪测量系统测量6 个十字叉丝半球十字叉丝交点坐标，用于双经纬仪测量系统坐标系与双目相机坐标系转站。因投影坐标系在双目相机坐标系下建立，其相对位置关系已知。通过坐标转换将双目坐标系反光点圆心坐标转到投影坐标系下，并计算反光点圆心在投影坐标系下激光出射方向单位矢量，输入到基于PROA-BP 的激光3D 投影振镜偏转电压预测模型中预测振镜偏转电压数值，将预测振镜偏转电压输入激光3D 投影机，投影机在标定板上投影出十字叉线。

使用双经纬仪测量系统测量十字叉线交点中心坐标，如图14 所示，将双经纬仪瞄准十字叉线交点中心后，解算双经纬仪测量系统坐标系下十字叉线交点中心坐标，当满足经纬仪解算十字叉线交点中心坐标RMS 小于0.02 mm 时，保存十字叉线交点中心坐标数据。不满足要求时，微调双经纬仪，直至满足要求。

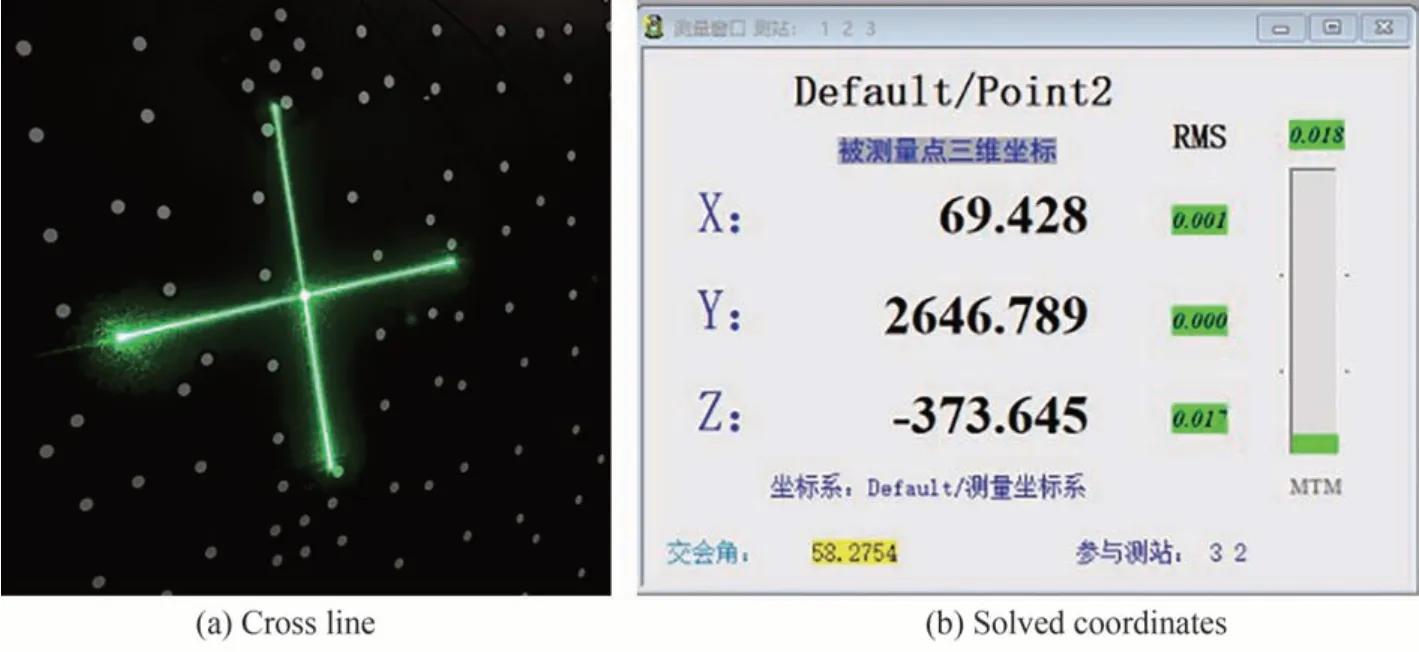
图14 测量十字叉线交点中心坐标Fig.14 Measure the center coordinates of the intersection points of the cross lines

已知双目相机坐标系下与双经纬仪测量系统坐标系下靶座上6 个半球球心坐标，可解算双经纬仪测量系统坐标系与双目相机坐标系相对位置，由于双目相机坐标系与投影坐标系相对位置关系已知，最终解算双经纬仪测量系统坐标系与投影坐标系相对位置关系，将双经纬仪测量系统测量的十字叉线交点中心坐标转换到投影坐标系下，并计算投影坐标系下十字叉线交点中心坐标与反光点圆心坐标的欧氏距离，并定义其为投影定位误差。

表3 是基于PROA-BP 神经网络投影模型预测投影实验部分数据。基于PROA-BP 的激光3D 投影振镜偏转电压预测模型的投影定位误差如图15 所示，投影定位误差约为0.35 mm，符合大多数激光投影定位场合，如孔位定位、零部件装配与定位和叶片铺贴定位等。

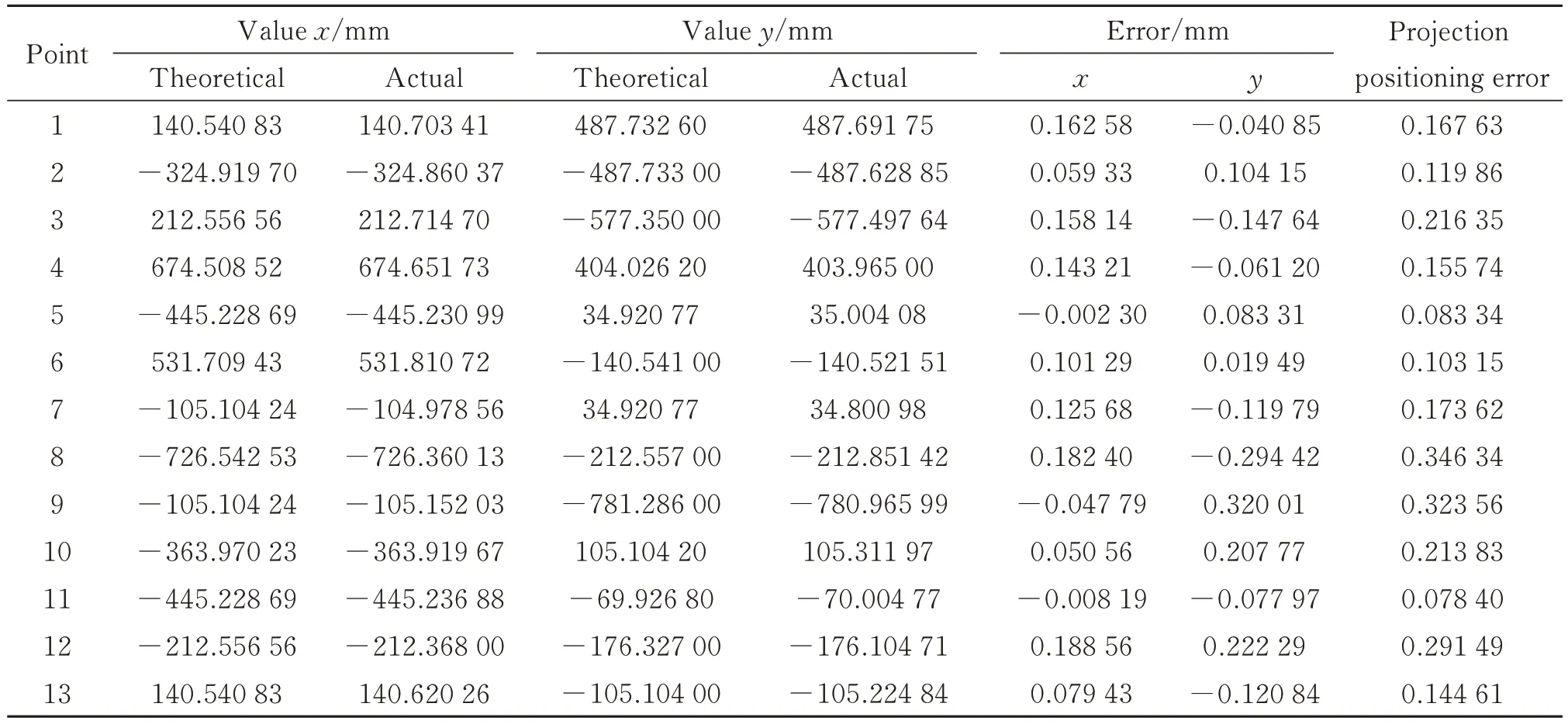
表3 基于PROA-BP 的激光3D 投影振镜偏转电压预测模型投影实验部分数据Table 3 Projection experiment part of the data of galvanometer deflection voltage prediction model of laser 3D projection based on PROA-BP

图15 基于PROA-BP 的激光3D 投影振镜偏转电压预测模型投影实验的投影定位误差Fig.15 Projection positioning error of projection experiment of galvanometer deflection voltage prediction model of laser 3D projection based on PROA-BP

6 结论

为提高激光3D 投影系统的投影定位精度，减小激光3D 投影系统振镜偏转角偏差与根据振镜偏转角标定的转轴公垂线长度e误差引起的投影系统综合非线性误差。本文设计了一种基于PROA-BP 的激光3D投影振镜偏转电压预测模型。利用PROA 优化BP 神经网络初始权重与偏置，解决神经网络容易陷入局部最优解问题。通过对比其他算法分析验证，结果表明，该算法的MSE 和MAE 均值分别为PSO-BP 神经网络的41.2%、62.4%，为BP 神经网络的22.2%、50.7%，证明该模型具有预测精度高、泛化能力强等特点。通过仿真与实验对该模型投影定位精度进行分析，并将其与激光3D 投影系统传统模型对比得到，该模型投影定位精度相较于激光3D 投影系统传统模型的投影定位精度提高约30%，可实现更高精度的辅助装配，并为激光3D 投影模型构建提供一种新的思路。