小学数学作业设计策略

吴团团

【摘  要】基于核心素养的发展要求，注重落实教—学—评的一致性，教师可以应用多元策略、可视化策略、迁移策略、变式策略、开放策略、整合策略设计作业，优化评价方式。

【关键词】核心素养;教学评一致性;探究性设计策略

《义务教育数学课程标准（2022年版）》研制了学业质量标准，提出“学业要求”“教學提示”，细化评价和考试命题建议，全面推进基于核心素养的评价，强化考试评价与课程标准、教学的一致性，促进教学与评价的有机衔接，凸显学生的主体地位，真正落实教—学—评的一致性。在“双减”背景下，作为教学工作中的重要一环——作业设计，需要教师整体把握教学内容，以结构化数学知识为载体，应用多种策略，基于多层次、大空间的设计思路，精心选择素材，给予学生高质量的作业挑战任务，发展学生的核心素养。

一、多元策略  丰富数学认知

多元表征就是让不同的学生采用自己熟悉的方式，喜欢的方式表达对数学知识本质的理解，促进学生内化吸收，构建数学模型。作业设计时，创设情境，通过操作表征、图形表征、语言表征、符号表征等多元表征方式，让学生多种角度来呈现数学思维，丰富认知，关注个性化思维表达，突破数学知识建构中的理解瓶颈。例如学习米、厘米后，结合教材习题设计认识尺和寸的拓展作业。

1.请你画一画，表示出1米、1尺和1寸之间的关系。

2.估一估1尺大约相当于几支铅笔长？

3.找一找生活中哪些物体的长大约是1尺、1寸。

4.制作一把以尺为单位的尺子，用它来测量生活中物体的长度。

通过阅读资料了解我国传统长度单位，了解米、尺、寸之间的关系，通过画图、操作，估算、寻找生活中1尺、1寸长的物体，制作尺子，积累数学活动经验，多元表征，数形结合，建立尺和寸的概念，丰富并发展量感。

二、可视化策略  搭建思维平台

荀子说：不闻不若闻之，闻之不若见之。有效地运用视觉，以视觉冲击引发思考，建模。课程标准将几何直观作为核心词之一，鼓励利用图形描述，整理、表达信息，将抽象问题形象化。教材中有大量图解示范，在课堂教学中，借助实物、课件演示、板演等一切与思维可视化有关教学手段的运用，都将数学思维具象化。遗憾的是很多老师将可视化的策略局限于教的策略，而学生亦不能自觉将画数学作为解决问题的有效策略。例如一个长方体沿着高截去4厘米的正方体，表面积减少96平方厘米，原来长方体的体积是多少？学生直接完成困难很大，但是借助草图，就能很快找出原长方体、截掉的正方体之间的联系，顺利解决。可视化的直观效果毋庸置疑。因此我们不但要在课堂上大张旗鼓去落实学生画数学能力的培养，作业设计时也关注画的能力的养成，让画不是散状的出现。

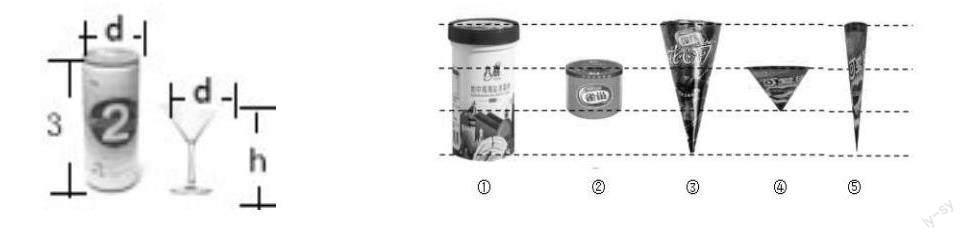
例如探究圆柱与圆锥关系的作业：

1.画圆柱与圆锥。①画等底等高的一对圆柱和圆锥。②画体积相等高相等的一对圆柱和圆锥。③画体积相等，底面积相等的一对圆柱和圆锥。

我发现：（   ）相等，（   ）相等，圆锥的（   ）是圆柱的（    ）

2.如下左图，家里来了7个同学，笑笑拿了一瓶饮料，每人一杯够吗？画一画表示你的想法。

3.如上右图，笑笑妈购买了一些冰淇淋，（  ）号冰淇淋体积是（  ）号冰淇淋体积的。你能找到几组，说一说你的想法。

作业1通过画图策略，让思维可见，更快发现1：3的关系。作业2没有具体数据，就是要创设情境，引领学生以画作为学习的拐杖，将圆柱转化为3个和圆锥等底等高的小圆柱，感受作图的优越性。作业3提供视角素材图，引领进行想象和转换，紧扣1：3的关系解决问题，灵活度高，开放性强。

开发促进思维发展的“数学画”的作业，设计提升数学读画、作画能力的习题，提升学生读图画图意识，发展思维能力。

三、迁移策略 构建知识网络

数学知识的学习要思考数学从哪里来，往哪里去，有什么用，打通知识之间的联系，形成网状结构。迁移能够帮助学生更容易理解新内容，主动把习得的方法思想类比，内化为数学学科的学习能力。作业设计时，教师要有大课程观，善于把握相似模块的知识框架体系，有机整合，形成整体思路与策略，培养学生发散思维。

例如学习小数简便运算，怎样做到高效又让学生饶有兴趣，主动探究？我们可以这样设计作业：

新课前：同学们，你们还记得整数的哪些运算律？赶快写下来。根据这些运算律，请搜集、编写相关的简便运算习题。

新课中：这些运算律对小数适用吗？请你创编小数简便运算相关的习题。

新课后：将45×78-55×78，25×32×125改编为小数简便运算的习题，能编多少道？

基于已有经验，从整体视角出发，将小数与整数的简算勾连。学习本部分内容，强调基于运算律知识系统的理解形成，引导学生把整数习得的方法迁移到新的问题情境中，进行类比同化，实现迁移。相信在以后学习分数的简便运算，学生也会主动勾连，构建简便运算的知识网络。

四、变式策略  提炼数学方法

数学学习活动应该引领学生理解数学本质，提炼数学思维。我们设计作业时应注重变式，创造有效的问题情境，激发学生利用已有的经验再迁移创造，去猜想，去经历，去探究，在不断变换的非本质属性面前，比较分析变与不变，聚焦数学本质、方法、思想，拓展延伸。

例如学习圆柱的体积，学生在大量的操作中进行观察比较，通过平面图形面积公式的推导过程，将转化图形—寻找联系—推导公式的方法，迁移应用到圆柱体积公式的推导中后，可以设计探究作业：

1.淘气猜想求右边两个图形的体积也能适用V=sh。请你验证淘气的猜想是否正确。说说什么样的图形适用V=sh。（单位：dm）

2.如右图，求图形的体积。教师应用变式策略，聚焦核心问题：什么样的立体图形的体积都适用V=sh？学生可以用两个完全一样的半圆柱体拼成1个圆柱，找出两个图形之间的联系：高相等，半圆柱体底面积为圆柱体的一半，体积也是圆柱的一半。这与三角形面积推导公式本质上是一样的，都是用倍拼法。学生在求环状柱体体积时，发现环状柱体体积=外圆柱体积-内圆柱体积，再应用乘法分配律进行整理变形：环状柱体体积=外圆柱体积-内圆柱体积=（外圆面积-内圆面积）×高=环形面积×高=底面积×高，感悟方法的一致性，归纳出直柱体体积公式。最后，作业引领学生运用新建构的数学模型解决新问题。求出其他直柱体图形的体积，实现由“一道题”到“一类题”的贯通。在变与不变，拓展延伸中，聚焦本质，提炼方法，增强猜想、类比、推理能力，发展空间想象力，提升思维。

五、开放策略  提升变通能力

探究性作业可以设计开放性作业，发散学生的思维，拓宽广度，思路。多種解法、多种答案中呈现出学生思路的全面性、有序性、灵活性。打破思维定势，提高变通能力，让学生体会知识的本质。

比如条件开放性：求右边这个图形的面积，至少需要几个条件？

本题考查学生观察分析能力，运用不同的割补法，综合多边形的面积公式，逆向寻求解决问题的充要条件，弹性强，少了无法解答，多则不必要。

比如解法开放：48×25你能想到几种方法？

解法一：48×25=（12×4）×25=12×（4×25）=12×100=1200

解法二：48×25=（48÷4）×（25×4）=12×100=1200

……

习题激发解决问题的热情，防止思维定势，可以用积变化的规律，乘法分配律。乘法结合律做出多种解答，发散学生思维，让学生的思维有驰骋的空间，在作业中体验属于自己的成功。

比如答案开放：如右图，以AB为底，画高为3厘米的三角形，你能画几个？观察这些三角形顶点的位置，你有什么发现？

抓住三角形高的本质，在线段AB的上下方，找到与AB的距离为3厘米的点，进行连接可以画出无数个三角形，渗透极限思想、等积变形的数学思想，为后续学习做好铺垫。

六、整合策略  提高学习效能

教材具有普适性，以课时形式用静态方式呈现，每新习得知识内容配套对应的课时作业，并在一定的新课后再辅以练习课进行巩固提升。教师如果只跟着教材按部就班展开教学，那么就会常常看到单调机械的重复练习，学生一看就会，一做就对，对作业甚是无感。教师根据学情对作业进行压缩、整合，让作业更有灵气，富有挑战性，尤为重要。例如学习小数乘法这一单元，笔者设计了一组作业。下面是垒球比赛中垒球落地时留下的球印记录图。

（单位：米）

1.笑笑扔了21米，妙想的距离是笑笑的1.52倍，上图中（  ）号球印是妙想投掷时留下的，写出你的想法。

2.一号球印是蓉蓉投掷时留下的，计算蓉蓉的成绩应选择（  ）算式。

A. 21×0.8 B. 21×1 C. 21×1.2 D. 21×1.9

3.小米的成绩是笑笑的1.2倍，下面有（  ）个算式计算结果与小米的成绩相等。

21×12÷10 21+21×0.2

21×12×0.1      20×1.2+1.2

A. 1 B. 2 C. 3 D. 4

以校运会为情境，融合小数估算，小数简便运算，积与乘数大小的变化关系等知识点，打破碎片化的作业模式。

第1题，运用估算或笔算21×1.52，发展数感。第2题，情境中的球印图，具有数线图的模型，运用积与乘数大小的关系进行逆向推理，要使积小于21，第二个乘数必须小于1。球印距离的远近和积的大小建立联系，数形结合，使抽象的推理具体化。作业3关注算法、简便运算、计算本质，让学生获得小数乘法的结构认知。

“双减”政策下，教师要有较强的作业设计能力。作业的设计，是一件具有创造性的工作，我们采用多种策略设计形式多样、富有探索价值的作业，使学生成为作业的主人、学习的主人。