基于HIFU回波信号和多尺度模糊熵的生物组织变性识别研究
2024-04-13李昂翟锦涛刘泽昊邹孝钱盛友
李昂 翟锦涛 刘泽昊 邹孝 钱盛友


收稿日期:2023-07-28;修回日期:2023-09-27。
基金項目:国家自然科学基金项目(12274200,11774088);湖南省教育厅优秀青年基金项目(22B0003);长沙市自然科学基金项目(kq2202239)。
作者简介:李昂,硕士研究生。
* 通信作者:邹孝,讲师,主要从事生物医学电子研究。E-mail: shawner@hunnu.edu.cn。
摘 要:为了解决高强度聚焦超声(HIFU)治疗中的监测问题,在无需引入其他监测源的情况下,通过研究HIFU回波基波与二次谐波的多尺度模糊熵(MFE),提出了一种生物组织变性辨析新方法。HIFU回波信号通过谱减法去噪后,利用信息散度优化的变分模态分解(KLD-VMD)提取其基波与二次谐波分量,然后结合基波与二次谐波的MFE对组织进行变性识别,并使用等错误概率(EER)评价了该方法的有效性。最后,研究还比较了KLD-VMD与VMD、经验模态分解(EMD)和固有时间尺度分解(ITD)等其他分解方法,结合MFE分析了其辨析变性组织的能力。试验结果表明:基于KLD-VMD和MFE的组织变性识别其EER达到5.1%,相较于其他方法表现出了更好的识别效果;结合基波和二次谐波的识别结果比使用单一特征参数更好。该研究为HIFU治疗提供了一种新的监测方法,具有潜在的实际应用价值。
关键词:HIFU回波信号;优化变分模态分解;多尺度模糊熵;生物组织损伤识别;肿瘤治疗方式
中图分类号:TN911.7 文献标志码:ADOI:10.3969/j.issn.1007-7146.2024.01.005
Identification of Tissue Damage Based on HIFU Echo and Multiscale Fuzzy Entropy
LI Ang, ZHAI Jintao, LIU Zehao, ZOU Xiao*, QIAN Shengyou
(School of Physics and Electronics, Hunan Normal University, Changsha 410081, China)
Abstract: To address the monitoring problem in high-intensity focused ultrasound (HIFU) therapy, a new method is proposed for identification of tissue damage without the need for additional monitoring sources. The method involves studying the multiscale fuzzy entropy (MFE) of the fundamental and second harmonic of the HIFU echo. The HIFU echo signal is denoised using spectral subtraction, and then the fundamental and second harmonic components of the signal are extracted using the kullback-leibler divergence-optimized variational mode decomposition (KLD-VMD) method. Finally, the MFE combining the fundamental and second harmonic is used to identify tissue damage. The validity of the method is verified using the equal error rate (EER), where a lower EER indicates better recognition. The study also compares the KLD-VMD method with other decomposition methods such as VMD, EMD, and ITD, in combination with MFE for tissue damage identification. The experimental results demonstrate that the tissue damage identification based on KLD-VMD and MFE achieves an EER of 5.1%, which is better compared to the other methods. Furthermore, the results also show that combining the fundamental and second harmonics improves the identification performance compared to using either echo alone. This study provides a new monitoring method for HIFU therapy with potential practical applications.
Key words: HIFU echo; optimized variational mode decomposition; multiscale fuzzy entropy; identification of biotissue damage; tumor treatment methods
(Acta Laser Biology Sinica, 2024, 33(1): 040-047)
高强度聚焦超声(high intensity focused ultrasound,HIFU)作为一种非侵入性的肿瘤治疗方式,能够通过热凝实现对生物组织的选择性治疗[1-2]。治疗期间进行实时监控是保证HIFU治疗安全高效的前提,现有的成熟监测手段包括计算机断层扫描(computed tomography,CT)、磁共振成像(magnetic resonance imaging,MRI)和超声成像[3]。然而,CT是基于X射线技术的,X射线的电离辐射对人体有害。MRI扫描时间长,对患者的身体运动敏感,容易产生伪影。相比于CT和MRI,超声成像具有设备兼容性好、更易实现等优点,但超声图像是由超声信号转换而来,转换过程本身中会造成信息的缺失[4]。从信号处理角度通过直接分析HIFU回波信号的特征用于实时监控和疗效评价,该方法无需引入其他监测超声源,可避免监测源和HIFU源之间的相互干扰。
在HIFU回波信号中,非线性特性会导致谐波成分的存在。基波与谐波结合信号分析方法可以准确地检测和分析这些非线性成分,帮助我们深入了解信号的本质以及信号与系统之间的关系。信号分解方法选取对基波和谐波成分的分离和获取至关重要。现有的经典信号处理方法中,本征时间尺度分解(intrinsic time-scale decomposition,ITD)方法对输入信号中的噪声可能敏感,这可能影响分解结果的准确性;经验模态分解(empirical mode decomposition,EMD)方法在抗噪声干扰方面存在优势,但存在模态混叠问题,不同的固有模态函数(intrinsic mode functions,IMF)之间可能出现明显的干扰或重叠,导致分离所需的信号成分困难[5];变分模态分解(variational mode decomposition,VMD)方法在EMD方法的基础上解决了模态混叠问题,但需要调整一些参数,如模态数和惩罚因子,以获得最佳的分解结果。选择这些参数可能具有主观性,并且可能需要反复尝试[6]。为此,本文使用深度学习算法中的KL散度(Kullback-Leibler divergence,KLD)[7]确定VMD的惩罚因子和模态数,避免了参数的主观性选择[8]。
当生物组织发生损伤时,HIFU回波信号的非线性特征会发生变化[9-10]。为了提取HIFU回波信号的非线性特征,一些研究者对样本熵(sample entropy,SE)[11]进行了分析,但任意两个相似距离超过固定值的粗粒度时间序列会导致SE不稳定[12]。另有研究者提出了模糊熵(fuzzy entropy,FE)来进行分析,FE引入了一个指数函数来确定两个任意时间序列的相似性,但其FE只在单一尺度上反映信号的复杂性和不规则性,无法反映信号的所有特征[13]。为此,本文结合基波与谐波的多尺度模糊熵(multiscale fuzzy entropy,MFE)[14],通过KLD-VMD对去噪后的HIFU回波信号进行分解,再结合基波和二次谐波的MFE识别组织损伤。
本文对HIFU回波信号进行研究,通过优化的VMD提取基波与二次谐波,结合基波与二次谐波的MFE对组织进行损伤识别,以更好地监测和评估HIFU治疗的安全性和有效性,为超声治疗提供损伤识别和疗效评估的新技术。
1 材料与方法
1.1 试验系统与流程图
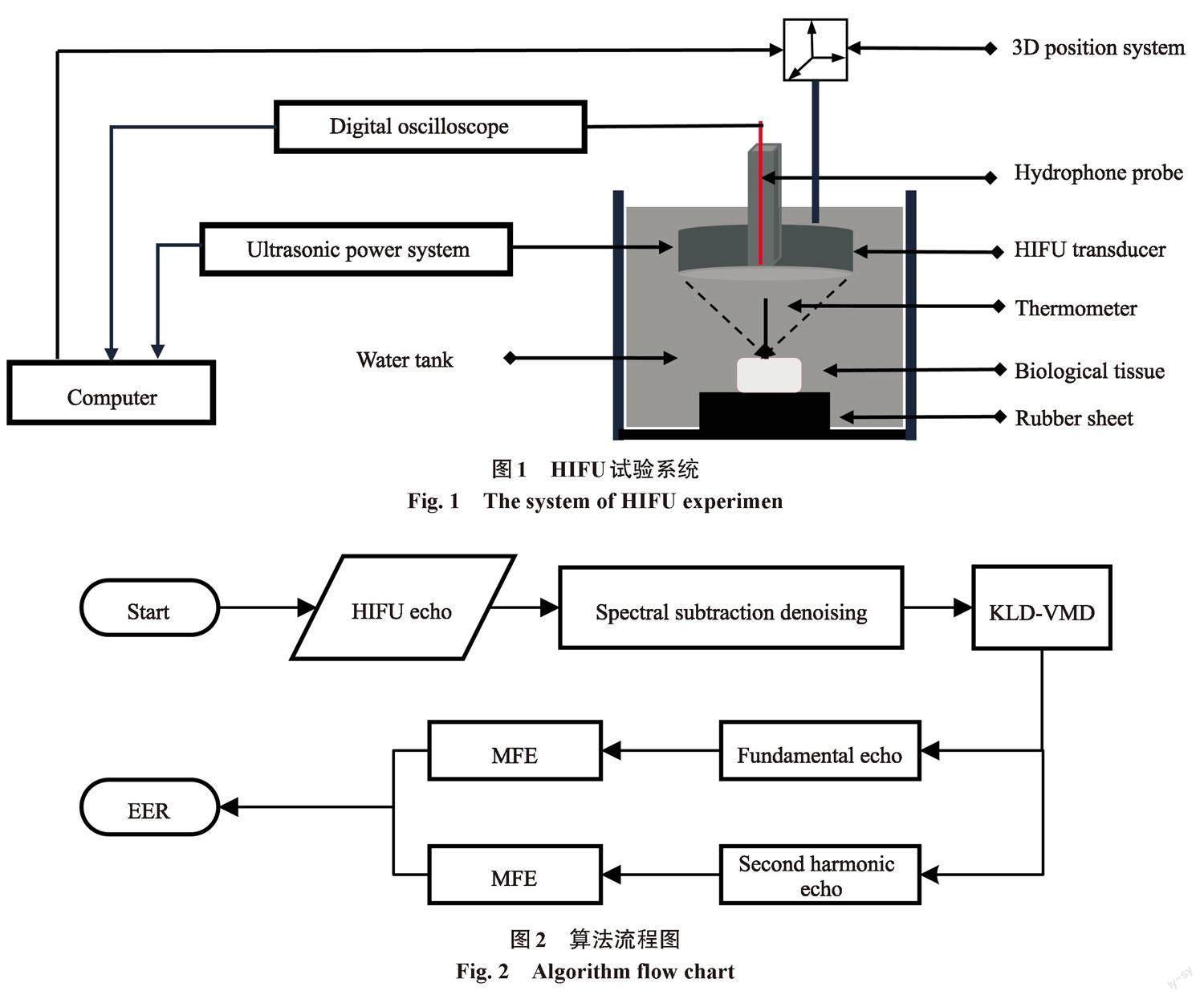
HIFU试验系统如图1所示。试验前需准备新鲜的离体猪肝组织固定在声学橡胶板上,再放置于HIFU源(PRO2008,Shenzhen,China)下的混合溶液中。HIFU辐照靶区的位置变化可以由计算机的3D定位系统控制。用热电偶(DT-3891G,Shenzhen,China)测量肝脏组织靶区域的温度。换能器的中空部分放置针式水听器来接收HIFU的回波信號。回波信号经过宽带信号放大器后,被数字示波器(MDO3032,Tektronix,USA)采样和保存。试验中HFIU回波信号的中心频率为1.39 MHz,二次谐波频率为2.78 MHz,采样点数为100 000。通过HIFU辐照新鲜离体猪肝脏组织,对组织进行切片并观察其是否出现凝固和变性。采集了400组信号,其中200组状态正常,200组出现了明显变性,各用100组正常与变性状态的数据进行训练,剩余200组作为测试数据。
试验采集信号之后,使用本文方法对信号进行处理与分析,其流程如图2。首先,对HIFU回波信号使用谱减法去噪,再使用KLD-VMD从多个模态中提取出基波与二次谐波分量。最后,结合基波和二次谐波的MFE进行分类判断组织是否变性。
1.2 谱减法
HIFU回波信号与噪声在时域无法区分,而在频域其能量有明显差异,因此,本文通过谱减的方式对HIFU回波信号进行去噪处理[15]。
纯净HIFU回波信号为x(n),噪声信号为z(n),则带噪信号的时域表达式为y(n):
y(n)=x(n)+z(n)(1)
对信号y(n)、x(n)和z(n)进行加窗分帧后做离散傅里叶变换(discrete Fourier transform,DFT)得到:
Yw(ω)=Xw(ω)+Zw(ω)(2)
对公式(2)等式两边同时求平方,可以得到带噪信号的功率谱为:
|Yw(ω)|2=|Xw(ω)|2+|Zw(ω)|2+2Re[Xw(ω)Z*w(ω)] (3)
式中,2Re[Xw(ω)Z*w(ω)]表示Xw(ω)和Zw(ω)在相关性作用下产生的分量。
对公式(3)两边取期望值E[.],可得:
E[|Yw(ω)|2]=E[|Xw(ω)|2]+E[|Zw(ω)|2]+2E{Re[Xw(ω)Z*w(ω)]}(4)
因为x(n)和z(n)之间互不干扰,所以交叉项2E{Re[Xw(ω)Z*w(ω)]}=0。试验环境不变的条件下,噪声频带范围基本不会变化,因此,对于公式(4)中噪声项可以使用前导无信号段估计噪声。基于信号的短时平稳特性,通过移项可得谱减处理后的纯净HIFU信号的估计功率谱:
|Xw(ω)|2=|Yw(ω)|2-|Zw(ω)|2(5)
对|Xw(ω)|2开平方后可得到信号的幅度谱估计值。去噪信号的相位可以用带噪信号的相位来代替,因此,增强处理后的纯净信号估计谱为:
Xw(ω)=|Yw(ω)|exp[jθYw(ω)](6)
公式(6)中,θ表示带噪信号的相位。最后,对Xw(ω)进行傅里叶逆变换,可以得到纯净信号的时域估计表达式:
xw(t)=F–1[Xw(ω)](7)
1.3 KLD优化变分模态分解
通过谱减法对HIFU回波去噪后,使用VMD方法提取出基波与二次谐波。VMD的约束条件为所有模态之和与原信号相等[16],约束表达式为:
mim ∑kk=1 ‖?t[(δ(t)+)*uk(t)]e–jωkt‖22
s.t. ∑kk=1 uk=xw(t)(8)
公式(8)中:?t为对时间t求偏导;δ(t)为狄克拉函数;uk和ωk为分解后第k个模态分量和中心频率;*为卷积运算符。
引入Lagrange乘数因子λ和惩罚因子α,解决公式(9)约束最优化问题,并通过交替方向算法等待优化序列,得到原始信号模态函数及中心频率表达式:
?k,n+1(ω)=(9)
ωk,n+1=(10)
对模态函数和中心频率进行更新:
λn+1=λn+σ(f(ω)-∑k ?k, n+1)(11)
其中,λ为Lagrange乘数因子;σ为更新因子。对公式(10)~公式(11)进行迭代:
<ε(12)
式中,ε为收敛标准容差。
由公式(9)~(12)可知,VMD使用迭代搜索变分模型最优解,确定原始信号模态函数及其中心频率,最终原始信号分解为k个固有模态函数[17]。
在概率论和信息论中,KLD是用来描述两个概率分布P对Q之间关系的一种方法[19]。设模态数k=[2,10],求出各个k值条件下模态函数?k,n+1(ω)与原信号xw(ω)的KL散度,剔出虚假模态分量,并在确定模态数k的条件下,寻找最佳的惩罚因子α:
IKL(?k,n+1, xw)=∫?k,n+1(ω)lndω (13)
1.4 MFE
提取HIFU回波信号的基波与二次谐波分量后,计算它们的MFE作为特征参数进行损伤识别。计算方法如下[18-19]:
1) 对基波和二次谐波的时间序列进行粗粒化转换,得到新序列:
xb(τ)= ∑bτ xc, 1≤b≤N/τ (14)
其中,τ是比例因子。当τ=1时,{xb(τ)}为原始数据{xc}。当τ>1时,原始数据被分成长度不超过N/τ的粗粒化序列{xb(τ)}。
2)确定嵌入维度m,并对序列进行空间重构:
Xim={x(i), x(i+1),……, x(i+m-1)}-u0(i)
(i=1,……, N/τ-m+1)(15)
其中u0被定义为从i点开始的m个连续样本的平均值,x(i+k)是{xb(τ)}的(i+k)项。当m=1时,新序列长度与粗粒化序列长度相等。当m=2时,新序列的长度为 N/τ-1,这导致了多尺度信息熵的信息量不足。然而,当m太大时,数据之间的耦合会降低。因此,嵌入尺寸m通常取为3、4、5。
3)向量和向量之間的距离被定义为两个向量的对应元素的最大差值:
Dmih=max|x(i+k)-x(h+k)|(16)
4)两个向量的相似度被模糊隶属度函数μ=(x,r)定义,
Dmih=μ(dmih, r)=exp[-](17)
其中,μ=(x,y)是指数形式的模糊隶属度函数,r和2分别是边界的宽度和梯度。
5)Am(r)是模糊函数的子函数,其定义为:
Am(r)= ∑N-m | ∑N-m Dih|(18)
6)确定模型的嵌入维度为m+1,并重复步骤1)到步骤5)得到Am+1(r)。
7)时间序列的多尺度模糊熵定义如下:
MFE(m, τ, r, N)=FuzzyEn(m, τ, xa(τ))
FuzzyEn(m, r, N)=-ln(19)
1.5 评价指标
等错误概率(equal error rate,EER)是一种生物识别安全系统指标。我们选取组织损伤的MFE阈值后,通过标签值计算试验数据的EER来评价分类效果,EER越低分类效果越好。分类问题中,若两个样本为同类,却被系统误认为异类,则为错误拒绝案例[20-21]。错误拒绝率(false rejection rate,FRR)为错误拒绝案例在所有同类匹配案例中占的比例,其定义为:
FRR=(20)
其中,FN为错误拒绝的案例(false negative),TN是正确拒绝的案例(true negative)。
若两个样本为异类,却被系统误认为同类,则为错误接受案例。错误接受率(false acceptance rate,FAR)为错误接受案例在所有异类匹配案例的比例,其定义为:
FAR=(21)
其中,FP为错误接受的案例(false positive),TP是正确接受的案例(true positive)。
调整阈值使得FRR=FAR,从而得到EER:
EER=FRR=FAR(22)
2 结果与分析
2.1 基于谱减法去噪和KLD-VMD信号分解
在选取同一段HIFU回波信号的条件下,通过谱减法降低HIFU信号的环境噪声。图3a和3b为试验采集的HIFU回波信号及其频谱,图3c与3d为谱减法去噪后的波形及其频谱,对比可知,频谱图中全频带噪声分量明显降低,去噪效果明显。HIFU回波信号的时域波形分解后会产生多个分量,我们通过频谱图选出基波与二次谐波分量。图4是对去噪信号使用KLD-VMD方法分解后得到的基波和二次谐波分量的频谱图,左图为基波的频谱,右图为二次谐波的频谱,观察频谱可以发现,干扰分量进一步减少,信号分解效果良好。
2.2 基于多尺度模糊熵的变性识别
2.2.1 嵌入维度与比例因子选取
为了选取适合的嵌入维度m与比例因子τ计算MFE,本文采用KLD-VMD方法提取基波与二次谐波后,分别对不同嵌入维度(m=3,4,5)和比例因子(τ=1,2,3…16)的取值识别效果进行了比较。组织损伤前后的MFE差异如图5所示,左图是基波的MFE,右图是二次谐波的MFE。随着嵌入维度m的增加,组织损伤前后的基波与二次谐波MFE差异变小。当嵌入维度为3时,组织损伤前后的熵差异大于其他两个嵌入维度的差异。因此,在后续对比例因子的研究中,选嵌入维度m=3。图6显示了在不同比例因子下,组织损伤前后的MFE具有一定的可区分性,τ=5时基波与二次谐波的MFE差异性最大。综上所述,当嵌入维度m和比例因子τ取值分别为3和5时,正常和变性组织对应HIFU回波信号的MFE相差最大,更有利于损伤识别。我们对其他信号分解方法也做了同样的试验,得到了相应的嵌入维度m与比例因子τ。
2.2.2 基波与二次谐波结合的损伤识别分析
在嵌入维度为3、比例因子为5的情况下,组织损伤前后的基波与二次谐波的MFE区分度达到最大,有利于组织损伤识别。但是,正常组织的MFE与损伤组织的MFE仍存在一定混叠,如图7所示。将混叠区域所有的MFE依次作为变性阈值,并通过标签值计算此时的EER评价变性识别效果,选取EER最低的MFE为变性的最佳阈值。对基波和二次谐波联合分析时,只有两个分量都满足变性条件,才能判定组织变性。
本文引用EER作为损伤识别评价指标,EER越低,生物识别系统的准确度越高。表1显示了使用单独一个特征参量或结合基波与二次谐波的MFE进行损伤识别的最佳阈值及EER,其中结合信号方法的EER为5.1%,比使用基波识别降低了0.6%,比使用二次谐波降低1.0%。因此,使用结合基波与二次谐波的MFE進行损伤识别的错误率更低,识别效果更好。
2.3 不同信号分解方法的损伤识别分析
为了验证KLD-VMD结合MFE进行损伤识别的优势,表2对比了不同分解方法的损伤识别效果。在使用基波的MFE进行损伤识别的情况下,KLD-VMD方法的EER为5.7%,相比VMD、EMD、ITD方法分别降低了3.7%、7.3%、7.6%。在使用二次谐波的MFE进行损伤识别的情况下,KLD-VMD方法的EER为6.1%,比VMD方法降低了4.5%,比EMD方法降低了7.4%,比ITD方法降低了7.9%。在使用结合基波与二次谐波的MFE的情况下,KLD-VMD方法的EER为5.1%,与其他三种方法相比EER分别降低了2.6%、5.8%、6.0%。综上所述,通过KLD-VMD方法分解信号后计算MFE进行损伤识别比VMD、EMD、ITD的效果要好。相较于使用单一谐波分量,基波与二次谐波结合损伤识别效果更好。
3 讨论
HIFU治疗过程中组织损伤可导致组织结构和特性的改变,而回波信号在不同损伤程度的组织中存在差异,其基波和二次谐波信号的特征提取可以提供有关组织损伤程度的重要信息。本研究提出了一种基于HIFU回波信号和多尺度模糊熵的生物组织变性识别方法,对去噪后的回波信号进行VMD分解,计算提取的基波和二次谐波MFE作为特征参数,并使用EER指标评价了该方法的有效性。结果表明,结合基波和二次谐波的MFE对组织变性识别表现出更好的效果,可为HIFU治疗实时监测和疗效评价提供参考。本文未来的工作将从以下几个方面展开:扩充生物组织样本数量和样本种类,提升方法的泛化能力;选择更有效的分类算法并优化算法结构,在变性识别的基础上进一步探索组织损伤程度分级评价;在临床实践中验证其可行性和实用性,将信号处理方法更好地应用于超声医学治疗。
参考文献(Reference):
[1] SEHMBI A S, FROGHI S, DE ANDRADE M O, et al. Systematic review of the role of high intensity focused ultrasound (HIFU) in treating malignant lesions of the hepatobiliary system[J]. HPB, 2021, 23(2): 187-196.
[2] LIU L, WANG T, LEI B. High-intensity focused ultrasound (HIFU) ablation versus surgical interventions for the treatment of symptomatic uterine fibroids: a meta-analysis[J]. European Radiology, 2022, 32: 1195-1204.
[3] YAMAGUCHI T, KITAHARA S, KUSUDA K, et al. Current landscape of sonodynamic therapy for treating cancer[J]. Cancers, 2021, 13(24): 6184.
[4] 黃峥, 颜上取, 邹孝, 等. 基于超声图像语义分割的HIFU治疗目标区域提取方法[J]. 计算机辅助设计与图形学学报, 2022, 34(5): 693-700.
HUANG Zheng, YAN Shangqu, ZOU Xiao, et al. Extraction method of target region for HIFU therapy based on ultrasonic image semantic segmentation[J]. Journal of Computer-Aided Design & Computer Graphics, 2022, 34(5): 693-700.
[5] MENG D, WANG H, YANG S, et al. Fault analysis of wind power rolling bearing based on EMD feature extraction[J]. CMES-Computer Modeling in Engineering & Sciences, 2022, 130(1): 543-558.
[6] LI Y, TANG B, YI Y. A novel complexity-based mode feature representation for feature extraction of ship-radiated noise using VMD and slope entropy[J]. Applied Acoustics, 2022, 196: 108899.
[7] 王常科, 马琼, 蔡清裕, 等. 深度学习在皮肤OCT医学图像中的应用[J]. 激光生物学报, 2023, 32(3): 193-199.
WANG Changke, MA Qiong, CAI Qingyu, et al. Application of deep learning in OCT medical images of skin[J]. Acta Laser Biology Sinica, 2023, 32(3): 193-199.
[8] JI S, ZHANG Z, YING S, et al. Kullback-leibler divergence metric learning[J]. IEEE Transactions on Cybernetics, 2020, 52(4): 2047-2058.
[9] WANG Z, HE X, SHEN H, et al. Multi-source information fusion to identify water supply pipe leakage based on SVM and VMD[J]. Information Processing & Management, 2022, 59(2): 102819.
[10] KAUR C, BISHT A, SINGH P, et al. EEG Signal denoising using hybrid approach of variational mode decomposition and wavelets for depression[J]. Biomedical Signal Processing and Control, 2021, 65: 102337.
[11] YAN S Q, ZHANG H, LIU B, et al. Identification of denatured and normal biological tissues based on compressed sensing and refined composite multi-scale fuzzy entropy during high intensity focused ultrasound treatment[J]. Chinese Physics B, 2021, 30(2): 028704.
[12] KUMAR A, ZHOU Y, XIANG J. Optimization of VMD using kernel-based mutual information for the extraction of weak features to detect bearing defects[J]. Measurement, 2021, 168: 108402.
[13] LIU B, ZHANG X, ZOU X, et al. Biological tissue damage monitoring method based on IMWPE and PNN during HIFU treatment[J]. Information, 2021, 12(10): 404.
[14] QIN A, MAO H, SUN K, et al. Cross-domain fault diagnosis based on improved multi-scale fuzzy measure entropy and enhanced joint distribution adaptation[J]. IEEE Sensors Journal, 2022, 22(10): 9649-9664.
[15] ZHAO Y, FAN Y, LI H, et al. Rolling bearing composite fault diagnosis method based on EEMD fusion feature[J]. Journal of Mechanical Science and Technology, 2022, 36(9): 4563-4570.
[16] XU D, SHAO J, GE J, et al. Research on weak signal feature extraction method of rolling bearing based on refined composite multi-scale weighted entropy[J]. Machines, 2022, 10(12): 1155.
[17] DIDDI S V S, KO L W. Course-grained multi-scale EMD based fuzzy entropy for multi-target classification during simultaneous SSVEP-RSVP hybrid BCI paradigm[J]. International Journal of Fuzzy Systems, 2022, 24(5): 2157-2173.
[18] YAN S Q, HUANG Z, LIU B, et al. The auto-regressive model and spectrum information entropy judgment method for high intensity focused ultrasound echo signal[J]. Applied Sciences, 2021, 11(20): 9558.
[19] WU Y, MA X. A hybrid LSTM-KLD approach to condition monitoring of operational wind turbines[J]. Renewable Energy, 2022, 181: 554-566.
[20] LIU Z, LIN Y, CAO Y, et al. Swin transformer: hierarchical vision transformer using shifted windows[C]//Proceedings of the IEEE/CVF international conference on computer vision, 2021: 10012-10022.
[21] XIAO J, LI J, YUAN Q, et al. A dual-UNet with multistage details injection for hyperspectral image fusion[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 60: 1-13.
