基于整体视角 强化核心概念
——以“质因数”贯通小学初等数论内容复习的思与行
2024-04-12陕西西安市未央区崇文路小学710021
陕西西安市未央区崇文路小学 (710021) 陈 妮
陕西师范大学附属小学 (710119) 郝高峰
纵观整个小学数学的学习内容,五年级历来以难点多、概念多、问题多的“三多”现象著称。初等数论的启蒙知识便集中在五年级。如贲友林老师在教学“因数与倍数(复习)”时就和学生罗列了11种“数”(因数、倍数、质数、合数、最大公因数、最小公倍数、质因数、奇数、偶数、公因数、公倍数)。这些名称各异的“数”,有的是具有某一类特征的数的统称,如质数、合数等,有的是刻画数与数之间的关系,如因数、倍数等。面对如此多的“数”,学生在学习中常会出现由“易”到“难”的过程,刚开始学习“倍数和因数”时,学生都觉得简单易学,随着学习进程的推进,烦恼随之而来——概念间相互干扰,易混难辨,复习时更是“剪不断,理还乱”。归根结底,还是对概念理解不透的缘故。那么,如何改变这一现状呢?基于整体视角,强化核心概念应是一个有效的策略。当前的数学课堂,多以“因数”和“倍数”的概念统领其他概念,这本无可厚非。但笔者认为还可以在期末复习时再进一步,以“质因数”作为核心概念,如此才能有效贯通初等数论在小学阶段的有关内容,触及知识的本质。
一、思考
为什么要在期末复习时强化“质因数”这个概念?又为什么说“质因数”触及知识的本质呢?
(一)算术基本定理
众所周知,算术基本定理是初等数论中一条非常基本且重要的定理,它把对非零自然数的研究转化为对其含有的最基本的元素,即质数(素数)的研究。算术基本定理可以表述为:任何一个大于1 的自然数都可以分解为若干个质数的乘积,而且分解是唯一的。这与小学数学中的分解质因数相对应。可以说,数论研究的本质就是质数性质的研究。
质数的英文为“prime number”。Prime number之所以最终被翻译为“质数”,是因为从因数分解的角度看它是不可再分的。而合数可以看作是由若干个质数“合”成的。可见,任何一个大于或等于2的自然数都与它的质因数有密切关系。即质数本身就可以看作它自己的质因数,而合数则是由它的若干个质因数的积“合”成的。从质因数的角度研究自然数更有利于触及其本质。
(二)教学中对“质因数”的处理
现行教材中有关“质因数”内容的呈现方式不尽相同,“留”却不能尽其用,“舍”偏又“舍不得”,颇有“食之无味,弃之可惜”之感。现以下面三个版本的教材为例予以比较(见表1)。

表1 三个版本的教材中的“质因数”知识
通过比较不难发现,为了减轻学生的学习负担,各版教材在“因数与倍数”单元中均有明显淡化质因数概念的意图。其中,人教版教材在教学因数、质数的概念时并未提及质因数,只在“分数的意义和性质”单元中,因约分和通分要用到最大公因数和最小公倍数的相关知识,才在“你知道吗”栏目中简单提及“分解质因数”及“短除”;北师大版教材虽未提及“质因数”等概念,却在“因数与倍数”“分数的意义”两个单元中多次以“你知道吗”的形式提及相关内容;苏教版教材虽然通过例题明确引出质因数、分解质因数的概念,却再无下文。尽管如此,但也从另一个侧面说明,各版本教材都认为“质因数”这部分内容不能随意从教材中移除。
实际教学更是如此。囿于各种原因,虽然有争论,但大部分教师还是会补充相关内容,不过也和教材一样,只是将“质因数”“分解质因数”作为短除或者短除法求最大公因数与最小公倍数的附属品,并没有充分挖掘其所蕴藏的数学教育价值。
(三)“质因数”的教学价值探寻
这部分的所有概念均源于“因数”和“倍数”两个概念。比如质数是只有1 和它本身两个因数的数;偶数是有因数2(或是2的倍数)的数等。质因数也不例外,它是质数和因数的组合体。因此其他概念表面上都可以越过“质因数”,直接或间接与“因数”建立起联系,从而形成一个庞大的概念网。需要教师注意的是,这些概念之间只是建立起了“形”上的联系,缺少“质”的沟通。基于算术基本定理,从“质因数”的视角反观这些概念,恰恰能实现这一点。
1.因数和倍数
因为因数和倍数本身就是一对相互依存的概念,所以我们只讨论质因数和因数的关系。从质因数的视角看,不难发现一个数的因数就是由其所含有的质因数决定的。比如12=22×3,那么20,21,22和30,31分别组合就会产生12 的6 个不同的因数。即1=20×30,2=21×30,4=22×30,3=20×31,6=21×31,12=22×31。
2.最大公因数和最小公倍数
因为一个数的若干个质因数会“合”成它除1以外的所有因数,所以几个数的公因数当然是由它们公有的质因数合成的(1 除外)。那么最大公因数就是几个数所有的公有质因数的积。而最小公倍数不仅包含几个数公有的质因数,还得乘上它们各自独有的质因数。短除法只是简洁地记录了这一过程。在最小公倍数的基础上不断增加质因数,就会构成其他的公倍数。如A=2×3×3,B=2×3×5。(A,B)=2×3=6,[A,B]=2×3×3×5=90。
3. 2、3、5的倍数的特征
2 和5 的倍数特征看个位,恰恰是因为10 只含有2和5两个质因数,即10=2×5。可见,一个整十数一定是2或5的倍数,所以只看个位就可以了。3的倍数的特征看各个数位,也是因为9,99,999,……中含有质因数3。比如要判断354 是不是3 的倍数,之所以可以根据3+5+4=12来判断,是因为百位上的“3”表示的3 个100 可以看作3 个99 和3 个1,十位上的“5”表示的5 个10 可以看作5 个9 和5 个1,个位上的4 就是4 个1,而“3 个99”“5 个9”都含有质因数3,即是3的倍数,只需要考虑剩下的“3个1”“5 个1”和“4 个1”,而这恰好暗合了各个数位上的数字之和。同理,偶数和奇数(0 和1 除外)也和是否含有质因数2密切相关。
4.约分和通分
约分就是同时剔除分子和分母中的公有质因数的过程,即运用分数的基本性质将分子、分母同时除以它们的公有质因数,直至只剩下各自独有的质因数。通分就是不断增添分子和分母的公有质因数的过程。这里分子、分母同乘4 就相当于同时2次增添共有质因数2。
通过“质因数”打通了这些概念之间的“隔断墙”,让这些在“因数”“倍数”概念统摄下的概念群真正融为一个整体后,“数”在学生的心中就不再是一个静态的、固定的符号。学生知道它可以变换成不同的样态后,在看见数,比如“20”时就会想:20是由2×2×5 合成的。这个想法也可以迁移到运算中。这样更利于学生深入研究数,并且逐步由“数”向“式”过渡。而这一切都植根于算术基本定理。
二、实践
在课时教学时,教师将“质因数”概念内隐其中,在一定程度上可以将难点分散,减轻学生的概念负担;在单元复习时,教师可以通过“因数”和“倍数”将精简后的诸多概念连成线、织成网,帮助学生整体建构知识体系。如此,到期末复习时,教师就可以捅破最后一层“窗户纸”,以“质因数”作为核心概念贯通小学“初等数论”内容复习,帮助学生拨云见日,明确知识的本质。基于此,笔者做了如下尝试。
(一)以“质数”为引,确立核心概念
【教学片段1】
师:在“因数与倍数”单元,我们学了许多不同的“数”,它们有些是一类数的统称,有些则反映了数与数之间的关系。你能分得清吗?
生1:偶数、奇数、质数、合数均表示一类具有共同特点的数;因数、倍数、公因数、公倍数、最大公因数、最小公倍数以及质因数等,是表示数与数之间的关系的数。
师:说得真好。那么在“偶”“奇”“质”“合”这四类数中,人们对哪一类数情有独钟?
生2:质数!因为它只有1和它本身两个因数。
生3:我还知道很多数学家都喜欢研究质数的性质。我们书上介绍过的“哥德巴赫猜想”就跟质数有关,我还听说过“孪生素数”呢。
生4:质数在密码学中还有广泛的应用!
师:质数,又叫素数。数学有一门分支叫“数论”,主要是研究自然数的性质,包括质数的性质。与质数相对的概念叫“合数”。我们常说“人如其名”,你有没有想过,质数“质”在哪里?合数又是由什么“合”成的呢?
生5:合数是由质数合成的。如6=2×3,6 就是由质数2 和质数3“合”成的。质数就是数的本质、数根,不需要用别的数合成。
师:合数20是由“2×2×5”“合”成的。我们知道,任何一个合数都能写成几个质数相乘的积的形式,而且如果不考虑顺序,这个分解式是唯一的。这几个质数都是这个数的因数,因此都叫这个数的“质因数”。今天的复习课,我们就围绕“质因数”展开。
(二)以“质因数”为核心,明晰概念本质
1.投石问路:探索“质因数”与“因数”的关系
【教学片段2】
师:老师写一个数,你们能找到它的全部因数吗?
(教师写A,众生摇头,教师继续写A=2×2×3。)
师:现在呢?
生1:我能确定2 和3 都是它的因数,也是它的质因数。
生2:4、6也是,因为2×2=4,2×3=6。
生3:还有12,2×2×3=12。
生4:还有1。因为1是所有非零自然数的因数。
师:我们来整理一下,A 的因数有1,2,3,4(2×2),6(2×3)和12(2×2×3),其实A 就是12。现在你有什么发现吗?
生5:我发现一个数的因数就是由它的质因数一个一个、两个两个,这样几个几个“合”成的。
生6:我发现用“质因数”找因数时会漏掉“1”,大家一定要记得加上“1”。
2.举一反三:自主沟通“质因数”与其他概念
【教学片段3】
师:同学们,你们想研究质因数与谁之间的关系?请以小组为单位,自主选择研究方向。注意用质因数的积的形式表示数,这样会更便于大家发现关系。(学生合作探究后交流)
组1:我们组研究的是质因数与最大公因数的关系。通过研究A=2×2×3,B=2×3×5 发现,最大公因数就是把它们公有的质因数乘起来(如图1)。我们还用列举的方法验证了A 是12,B 是30,它们的最大公因数是6。

图1
组2:我们选择用12 和18 来研究最小公倍数。12=2×2×3,18=2×3×3(如图2)。我们用短除法试了一下,除数2和3就是它们的公有质因数,最后剩下的商2是12独有的质因数,3是18自己独有的质因数。最小公倍数乘“一圈”原来是这个道理。我们还可以看出最大公因数乘“一边”的道理。
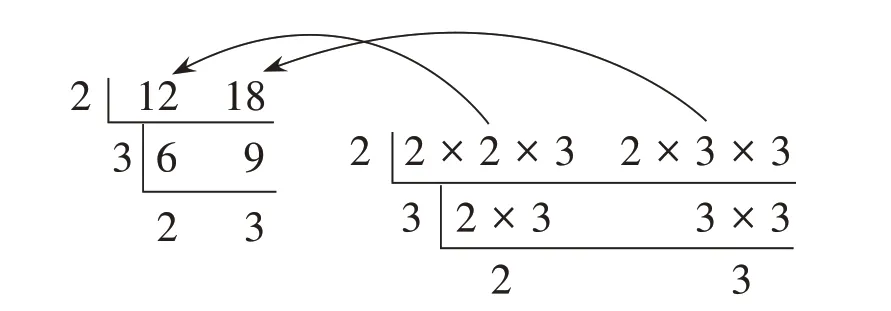
图2
组3:我们发现偶数都含有质因数2,而奇数都不含有质因数2。
组4:我们也研究了最大公因数和最小公倍数,发现在短除过程中可以很容易看清以前不明白的东西,比如“为什么两个数的积等于它们的最大公因数乘最小公倍数”。我们还用这种方式试了一下约分(如图3),这不就是划去共同的质因数嘛,太有意思了!
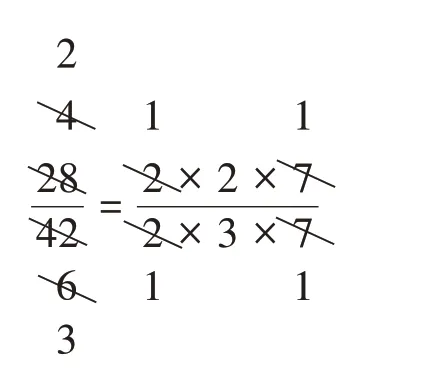
图3
师:同学们,如果说约分是划去分子、分母公有的质因数。那么,通分就是——
生(齐):不断增加它们的质因数。
(三)以“算术基本定理”为落脚点,筑起概念的“承重墙”
【教学片段4】
师:今天,我们从“质因数”角度更加深入地复习了这些曾经让我们眼花缭乱的概念。你们有什么想和大家交流的吗?
生1:让人茅塞顿开!质因数太厉害了!它竟然和这么多知识都有联系。
生2:我明白了以前没有想明白的一些问题。比如短除法中之所以在求最大公因数时乘“一边”,是因为边上的除数就是它们所有的公有质因数。这样乘起来一定是最大的。
生3:我觉得学习不能只记概念,弄明白背后的道理更重要。
生4:我知道了为什么人们那么爱研究质数,它真的很“质朴”!看到合数,我们也可以把它想成若干个质因数相乘的样子。
师:同学们,一个大于等于2 的自然数一定能分解成几个质数相乘的形式,而且这种分解方式是唯一的。这就是我们将来要学习的“算术基本定理”。正是有它的存在,我们才能透过“质因数”洞察这部分知识的本质。
总之,“因数与倍数”的教学需要教师立足整体视角,通过强化核心概念,帮助学生理解和掌握其中诸多的抽象概念,触及知识本质,完善知识结构。
