基于摄影测量的三轴土体剪切带演化规律

牟春梅，李刘悦，夏 燚

1) 桂林理工大学土木与建筑工程学院，桂林 541004 2) 广西岩土力学与工程重点实验室，桂林 541004

土体是一种多相多孔材料，与常规连续介质在力学特性上存在区别[1]，主要在于土体具有应变局部化的特殊性质，如发生渐进性破坏并形成剪切带[2]. 剪切带的出现是岩土材料即将失稳破坏的一个重要标志[3]，与滑坡、坍塌、地基失稳等工程地质灾害的发生密切相关[4]，对其深入研究有助于揭示土体发生剪切破坏的机理. 在剪切破坏的研究方法中，三轴试验能够接近真实地模拟实际工程中的土体受力条件[5]. 然而，常规三轴试验存在以下缺陷，如：根据排水量推算的轴向变形存在误差[6]；应变测量忽略了端部约束[7]，假定土样均匀变形，与实际发生的桶状变形严重不符. 因此，无法实现土样变形的局部测量，难以满足研究应变局部化现象的需求.

为实现三轴试验中土样变形的精准测量，许多学者将不同测量手段应用于局部变形的测定，如：布置LVDT(Linear variable differential transformer)位移传感器[8-9]、粘贴LDT (Local deformation transducers)局部应变片[10]、利用核磁共振透射[5,11]、进行X射线断层扫描(CT)[12-14]、结合数字图像相关方法[2,4,15-18]. 其中，数字图像相关方法与接触式测量相比，具有无扰动、操作简单、全表面测定的优势[19-20]，同时比外辐射式测量更灵活经济，已成为研究岩土材料变形破坏的常用手段[21-22]. 在1999年，Alshibli和Sture[15]通过相机拍摄土样表面格栅形图案的变化记录剪切带的形成过程，但该方法只能得到土样前表面变形[3]. 之后，邵龙潭和刘港等[16-17]将数字图像测量系统应用于三轴试验，由计算机处理图像得到试样变形，但该测量系统需对压力室进行改造，成本较高. 近期，有学者开发了一种新型摄影处理技术，并对其测量精度进行了验证及优化，得到了三轴试验中土样的三维应变场图，但未对其变形性质进行深入分析[22-24].

在以上学者研究的基础上，本文将数字图像相关测量方法(DIC)与土工试验相结合，运用摄影测量技术改良三轴试验，针对土样应变局部化现象进行深入研究. 试验设备无需改造，仅额外配置一台单镜头相机，实现了对土样全过程全表面的变形监测. 直接获取的土样表面变形更接近实际，所得本构关系和变形规律更为准确，据此对土样剪切带演化规律进行分析研究，能够得到更可靠的土样剪切带演变过程、演化模式及破坏机理.

1 摄影测量技术变形监测原理

将RAD(Ringed automatically detected)标记点布置在三轴试验仪器外表面和土样橡皮膜表面，如图1所示. 可定义三维重构模型的比例尺，构建测量对象所参考的世界坐标系，以此确定图像中各标记点在世界坐标系中的实际位置.

图1 改造后的标记体系Fig.1 System of identification after modification

经PM(PhotoModeler)图像测量软件，完成相机检校，求解相机参数. 使用经过校验的单镜头相机，在三轴试验中不同变形阶段对土样进行全方位拍摄，并保证每个标记点出现在三张以上的图像中，满足多相机成像原理，如图2所示，其中Si(i=1,2,3)为相机焦点，Pi(i=1,2,3)为图像平面，Ii(i=1,2,3)为图像物点，Q为实际物点. 通过Zhang提出的公式计算，完成由二维图像中的像素坐标系(m,n)像素物理坐标(x′,y′)、光心坐标系(x,y,z)，到世界坐标系(X,Y,Z)的逐一转换，具体公式可见文献[23]. 通过不同图像的视觉交汇，即可确定该标记点在三维世界坐标系中的深度，实现由二维图像转换为三维模型.

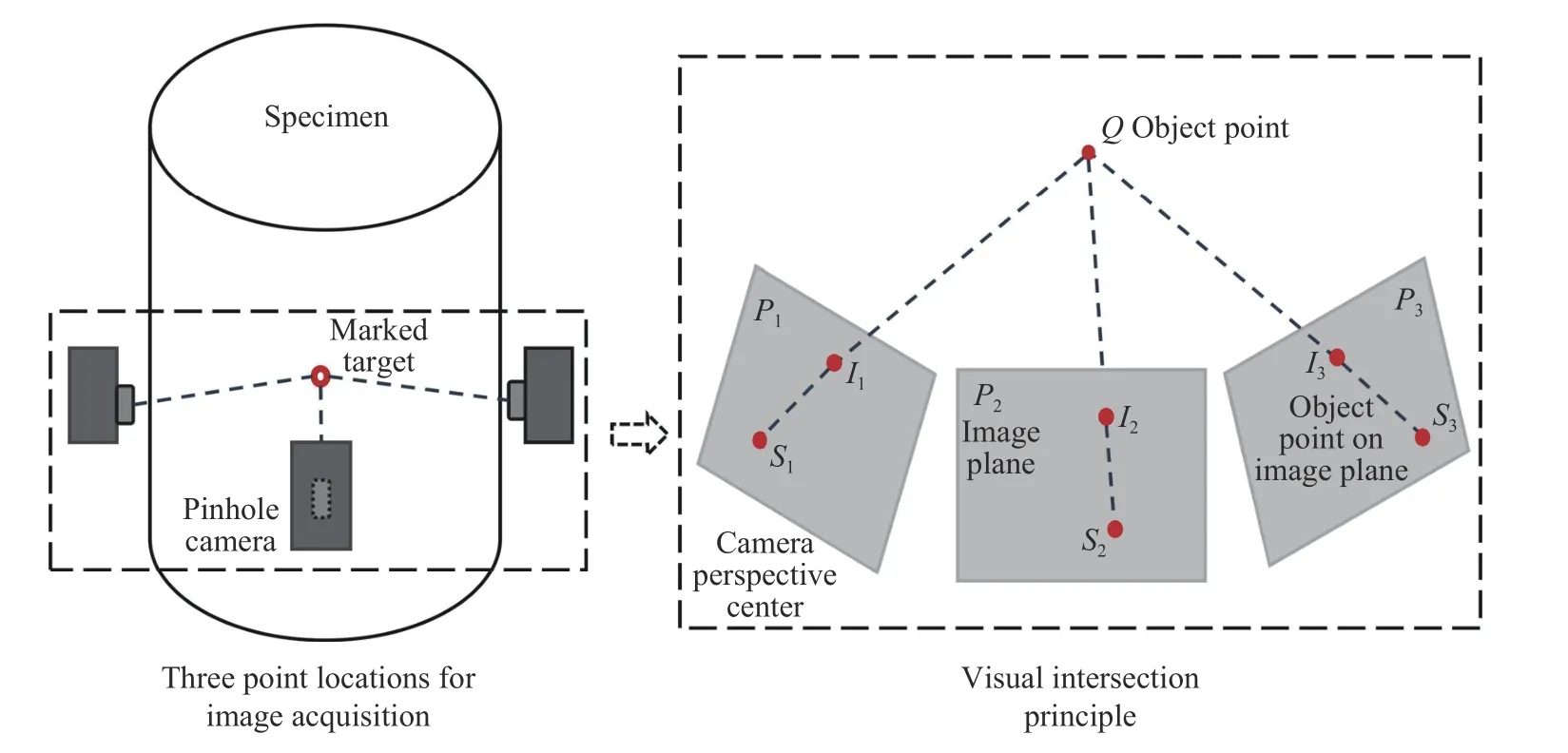
图2 多相机成像原理Fig.2 Multicamera imaging mechanism theory

采集图像时，光线在水–压力室玻璃罩–空气界面会发生双重折射，处理图像时需要进行校正. Li等提出了基于光线追踪的三维折射修正模型[23-24]，可以很好地消除折射带来的误差，其原理如图3所示，其中Di(i=1,2,3)为光线与压力室外表面交点，Ci(i=1,2,3)为光线与压力室内表面交点，Qi(i=1,2,3)为各条光线分别得到的物点，Q为最小乘法确定的实际物点.

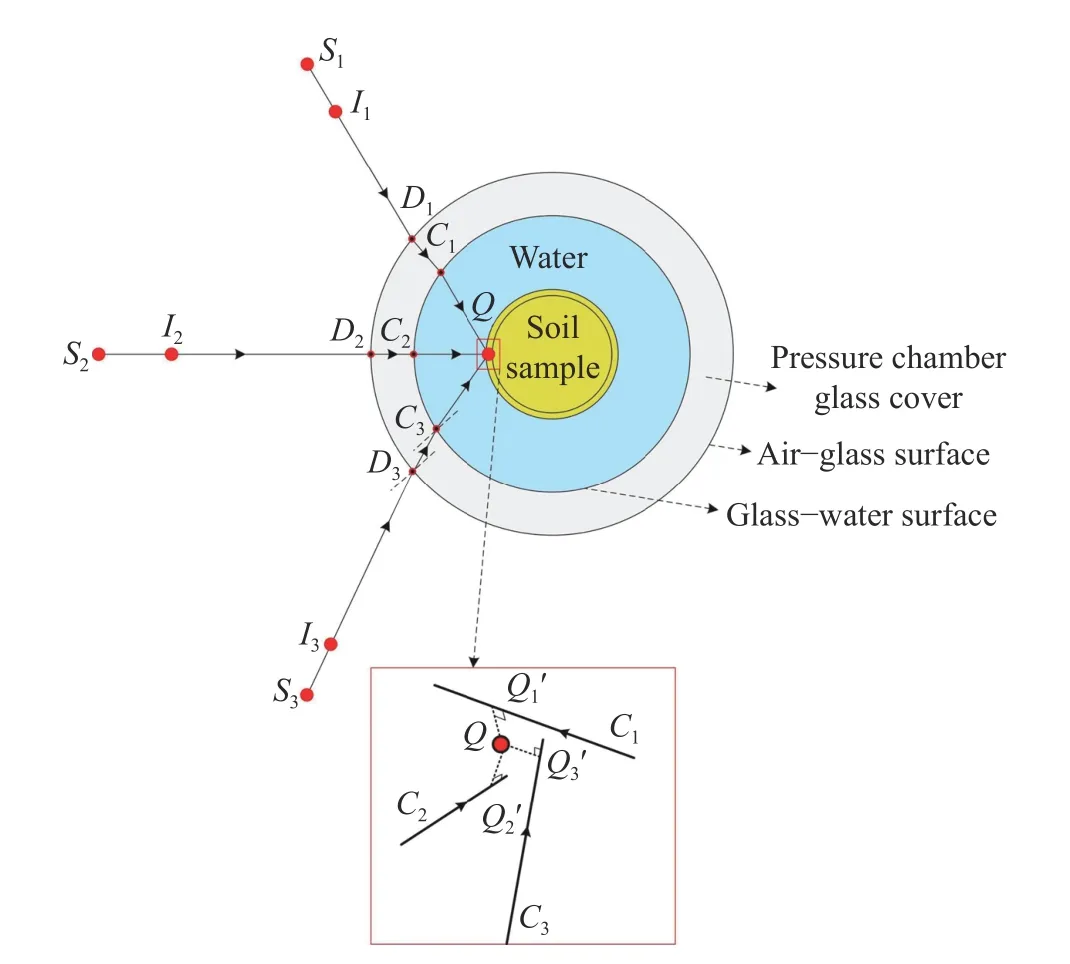
图3 折射校正示意图(据Zhang等[22]和Li等[24])Fig.3 Refraction correction schematic (according to Zhang et al.[22] and Li et al.[24])

首先，确定压力室折射界面数学计算模型，得到压力室材料折射率na和nc，及压力室表面D点处的法线方向单位向量. 然后，代入公式(1)计算，即采用光线追踪法校正，通过入射光线方向向量，求出玻璃罩折射后的光线方向向量. 最后，三条经过双重折射校正的光线在空间中交错相会，由最小二乘法确定标记点在三维世界坐标系中的唯一位置.

通过对土样表面136个标记点进行图像采集和数据处理，在Matlab中运行所整合的折射修正程序，并构建世界坐标系中“真实”的土样三维点云模型[25]，如图4(a)和(b)所示. 对模型运用boundrary边界函数，在不做任何假设下拟合得到土样各层边界，切合实际地还原土样三维重构模型，如图4(c)所示. 以此确定土样各层各点在三维空间中的变形状况，实现试验全过程全表面的变形监测.

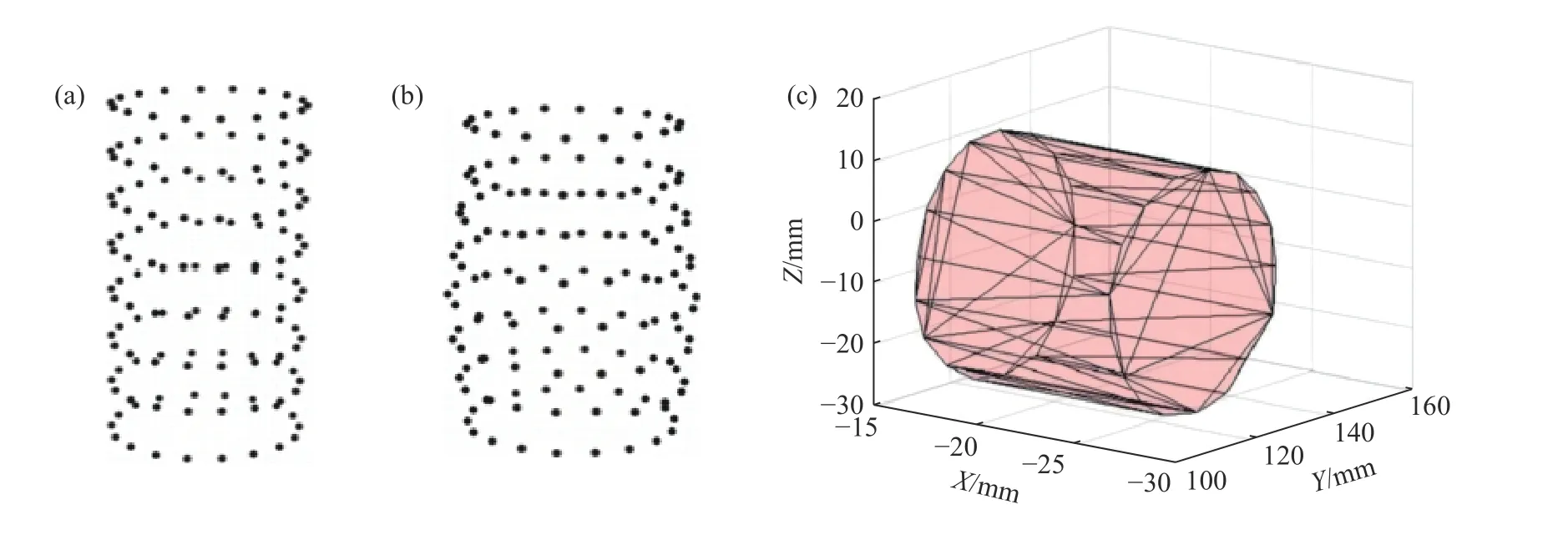
图4 土样三维重构模型. (a)轴向位移0 mm时和(b) 12 mm时的三维点云模型；(c)三角网格化的点云模型Fig.4 Three-dimensional reconstruction model of a soil sample: (a) three-dimensional point cloud model when the axial displacement is (a) 0 mm and(b) 12 mm; (c) point cloud model after triangulation

2 试验材料及方案

2.1 试验材料

本文以广西壮族自治区桂林地区广泛分布的红黏土为研究对象，表现为红棕色，具有较高的液塑限，粘性较高，其基本物理性质指标如表1所示.

表1 桂林地区红黏土基本物理性质指标Table 1 Basic physical properties index of red clay in the Guilin area

2.2 试验方案

试验采用常规三轴仪，对红黏土进行不固结不排水(UU)试验. 参照《土工试验规范》SL237—1999，将干密度为1.4、1.5 g·cm-3的饱和三轴土样各制备三组，分别进行围压为100、150和200 kPa的三轴试验，对试验按照N1～N6顺序编号，如表2所示.

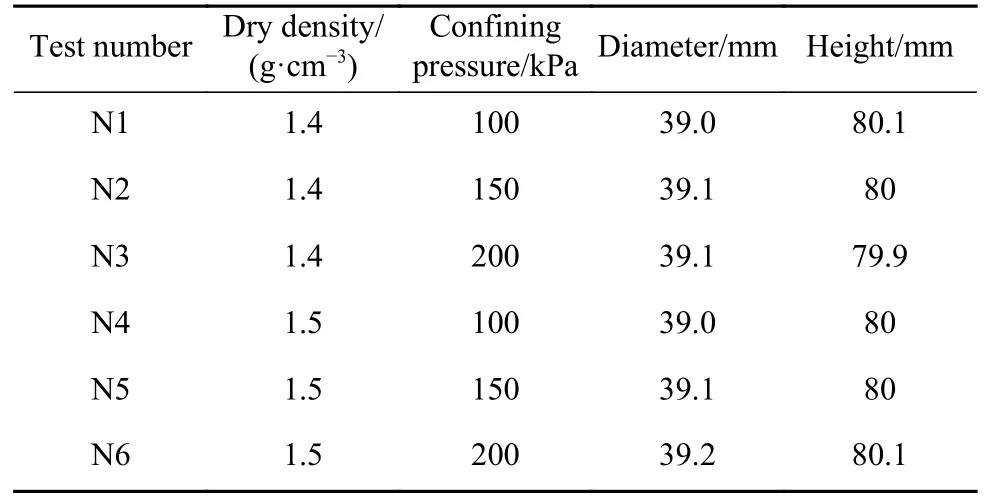
表2 三轴试验基本情况Table 2 Basic situation of triaxial tests

步骤如下：

1st：粘贴RAD标记点. 在三轴仪的压力室表面和两侧加载杆分别布置内径为1和0.9 mm的RAD标记点，如图1所示. 在土样表面橡皮膜上粘贴内径为0.8 mm的RAD标记点，轴向间隔10 mm，均匀布置8行、17列，共计136个标记点.

2nd：间歇性加载与图像采集. 采用位移控制式进行加载，加载速率为0.2 mm·min–1，轴向位移达14 mm时停止加载. 在试验开始前，环绕土样进行图像采集，当轴向位移达1、2、3、···、14 mm时，停止加载，重复土样图像采集.

3rd：数据后处理. 使用PM软件，提取所有变形阶段标记点和相机的三维空间相位信息，建立世界坐标系. 通过Matlab软件自编程序，进行折射校正，确定标记点实际的空间位置，构建土样三维点云模型，确定试验各阶段土样表面变形状态.

3 土样整体-局部应力应变特性

参考标记点的布置将土样分为八层，按照端部、中部将八层土样分为两个部分，如图5所示.每个部分的径向应变取所包含土层的径向应变平均值，根据实测径向应变数据计算土样轴向力的受力面积，进而确定各土层偏应力. 以N1、N3、N4、N6试验为例，对比摄影测量技术和常规方法分别得出的应力–应变曲线，其结果如图6所示.

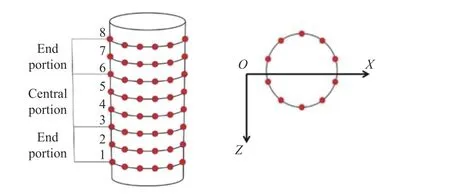
图5 土样分层示意图Fig.5 Schematic of soil sample stratification

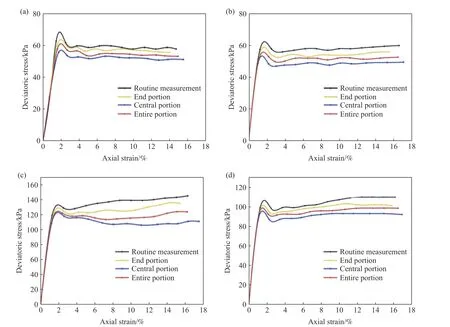
图6 土样N1、N3、N4、N6的应力–应变曲线. (a) N1; (b) N3; (c) N4; (d) N6Fig.6 Stress–strain curves of the soil samples: (a) N1; (b) N3; (c) N4; (d) N6

由图6可知，摄影测量技术测得的土样整体、中部、端部应力–应变曲线与常规方法测得的应力–应变曲线整体规律相似，均具有明显峰值. 尤其在试验初期三者基本重合，变形随荷载加大而呈现线性增长，而试验中后期逐渐出现差异. 这是因为土样实际发生“上下小、中间大”的桶状变形，而常规三轴试验假设均匀变形，与实际不符，所得轴向力受力面积偏小，土样强度偏大. 土样不受端部约束影响的部位变形更大、强度更低，摄影测量技术能够直观反映这种特性，测得中部的应力–应变曲线低于端部，整体的应力–应变曲线强度居中.而对于同一含水率的土样，围压200 kPa时比围压100 kPa时的偏应力峰值低，与常规三轴试验的规律不同，其原因可能与重塑红黏土存在薄弱环节相关. 可见，土样整体及局部具有不尽相同的受力变形性质，尤其在应变局部化现象中这种差异不可忽视，需要针对土样局部区域进行深入研究.

4 土样应变局部化现象分析

根据摄影测量技术所得受力变形数据，针对土样应变局部化现象演变的全过程进行分析更为可靠. 本节以试验土样N5为例，定义土样表面位于剪切带裂隙范围内的区域为剪切带内部区域，裂隙之外的区域为剪切带外部区域，如图7所示.

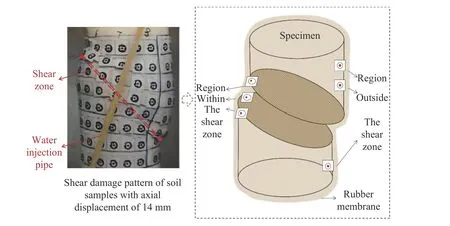
图7 土样表面的剪切带内外区域示意图Fig.7 Schematic of the shear band inner and outer regions on the soil sample surface

4.1 局部变形的应力-应变特性

经过摄影测量技术改良的三轴试验，可针对土样局部受力变形特性进行分析，确定土样表面任意一点的应力应变曲线. 由N5试验提取土样表面6个具有代表性的特征点进行研究，其中点1、点2、点3取自剪切带内部，点4、点5、点6取自剪切带外部. 各点的应变直接来自数字测量系统，据此得到各土层的平均应变和平均应力，各点的偏应力取各点所在土层的平均应力，得到各点应力应变曲线如图8所示.

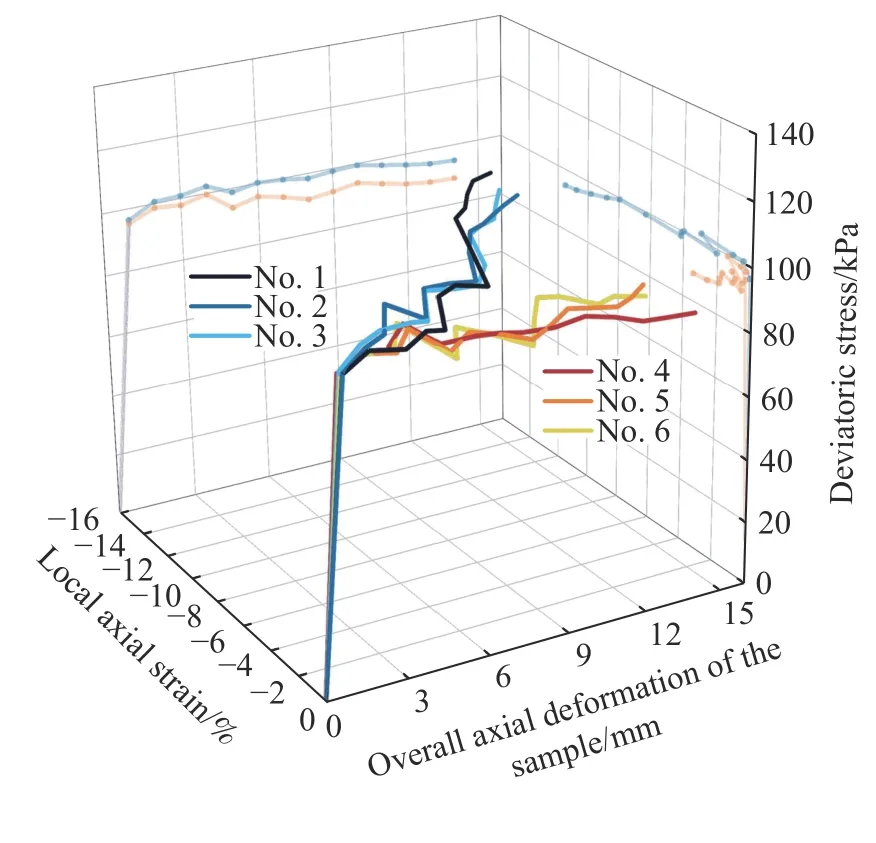
图8 土样表面特征点的应力–应变曲线Fig.8 Stress–strain curve of characteristic points on the soil surface

分析图8可知，在试验初始阶段，曲线几乎重合，说明变形均匀，两类特征点具有相似的应力应变特性. 随着变形不断增大，剪切带内外的特征点应力–应变曲线具有以下特性：同类型的特征点曲线保持相似，但两类特征点之间出现明显差异；剪切带内部区域的特征点应力–应变曲线偏高且靠后，偏应力和应变更大；随着变形持续增大，剪切带内的点应变不断升高，最高可达16.4%，而剪切带外的点应变不再增加，曲线逐步趋于平稳，最高为5.3%. 两类特征点分别代表了土的破坏区域与未破坏区域，其应力–应变曲线展现了土样不同区域的不同受力变形规律. 分析显示，剪切带内外点的力学表现具有明显差异，这种差异对剪切带的判别至关重要，有必要对局部区域进行针对性研究.

4.2 剪切带演化规律

摄影测量技术可以得到实验全程土样全表面的位移信息，根据大量的变形实测数据，针对土样应变分布进行统计分析可得到随剪切带演化的变形规律，据此提出一种基于土样应变判别剪切带发展阶段的方法.

4.2.1 剪切带内外区域的变形特性

以N5试验为例，通过摄影测量技术所得变形数据，处理得到土样表面剪切带外部及内部区域的平均应变，如图9所示. 以剪切带作为区分，其内外两个不同区域的变形存在明显差异，且差异随土样整体变形增大而加剧. 试验初始阶段，剪切带内外的平均局部应变基本一致；在土样整体轴向位移达3 mm时，曲线出现明显分叉；分叉后剪切带内部区域的平均局部应变曲线出现上下浮动后趋于平缓，而剪切带外部区域的在上下浮动后不断上升. 分叉前土样均匀变形，发生分叉意味着土样开始应变集中，剪切带内部区域变形不断增大，而外部区域变形趋于稳定. 因此，本文提出以分叉时刻作为剪切带开始形成的标志，N5试验的土样轴向位移加载至3 mm时剪切带开始形成.

图9 剪切带内外区域平均局部应变曲线Fig.9 Average local strain curve of shear band inner and outer regions on the soil surface

4.2.2 剪切带内外区域的应变特征值

针对位移控制式加载的各个阶段，统计N5试验土样表面相同局部应变的数量，取土样压缩为负值应变，膨胀为正值应变，得到土样轴向位移1 mm至6 mm间，136个土样表面局部变形量的分布情况，如图10所示. 在轴向位移达2 mm和3 mm时，变形量分布曲线在应变为–1.1%处出现明显落差.对比剪切带开始前后的曲线可见，3 mm时应变大于–1.1%的数量大幅增长. 轴向应变达4 mm后，剪切带进入发展扩张阶段，应变小于–1.1%的变形量分布有微小变化，而大于该值的分布变化较大.综上可判定，应变大于–1.1%的局部变形量是剪切带内部区域的变形量，随剪切带形成而出现，随剪切带发展而显著增多，且其分布均匀且分散，区域内的变形表现出明显的不均匀性. 而小于–1.1%的局部变形量来自于剪切带外部，随剪切带发展其数量不断减少，这部分变形量分布相对集中，变形相对均匀. 将剪切带在土样表面停止扩张作为其完全形成的标志，当土样整体轴向位移增大，土样表面测得剪切带外部区域的应变占比趋于稳定，则可认定剪切带已经完全形成. 即N5试验中，表面局部应变小于–1.1%的变形量占比不再变化时，剪切带完全形成.

图10 土样轴向位移1～6 mm间表面局部应变分布曲线Fig.10 Local strain distribution curve of the soil sample surface for axial displacements of 1–6 mm

4.2.3 局部变形量占比的变化规律

分别统计N5试验中应变小于–0.9%、小于–1.1%、小于–1.3%的局部变形量的数量，计算其在变形全场中的占比，占比随试验进度而变化的规律如图11所示. 在试验末期，应变小于–0.9%和小于–1.3%的占比曲线呈现上下波动，前者有降低趋势，后者则有所升高，说明小于–0.9%和小于–1.3%的局部变形量，涵盖剪切带内外两个区域，不能作为判别剪切带完全形成的标志. 而应变小于–1.1%的局部变形量占比曲线在试验末期走势平缓，表示在土样表面剪切带内的区域不再扩张，标志着剪切带的完全形成. 土样表面应变小于–1.1%的曲线在6 mm处出现明显拐点，之后保持平稳，该变形量的占比随试验进展趋于稳定，表明N5试验轴向位移加载至6 mm时剪切带完全形成.

图11 应变≤-0.9%、≤-1.1%、≤-1.3%的局部变形量占比曲线Fig.11 Local deformation ratio curves of strain ≤-0.9%, ≤-1.1%, and ≤-1.3%

4.3 剪切带演化过程

监测剪切带形成全过程的土样变形，得到土样轴向位移1～14 mm间，N5试验土样表面相同局部应变的分布，如图12所示.

图12 试验全程土样表面局部应变分布柱状图. (a) 柱状图正面；(b) 柱状图正面翻转180°Fig.12 Local strain distribution histogram of the soil sample surface throughout the test: (a) front of the distribution histogram; (b) distribution histogram flipped 180°

图12可见，N5试验应变分布随试验进度，展现出三个特征明显不同的区间：前期(1～3 mm)应变分布较为集中，中期(4～12 mm)出现分散，后期(13～14 mm)变形量突增且应变分布均匀. 结合上文剪切带发展阶段的判别方法，将中期区分为两个不同阶段，得到应变局部化现象的演化过程分为以下四个阶段，分别具有如下特性：

压缩变形阶段(N5试验轴向位移1～3 mm)：试验初期，土样表面的局部应变分布集中在0至–1%区间，说明不同区域的变形相对一致，土样发生均匀的弹性变形. 随着整体变形增大，应变逐渐集中，局部变形开始表现出差异，出现被剪切破坏的点. 在轴向位移3 mm时分布图出现明显分界，分界与图9中分叉点一致. 轴向位移达3 mm时，零散的破坏点逐渐相互连通，剪切带开始形成.

表面扩张阶段(N5试验轴向位移4～6 mm)：随着整体变形增大，应变分布由集中逐渐变得分散，应变集中不断加剧，表面变形量差距继续扩大，剪切带持续发展. 破坏的区域不断扩张，最终土样表面的剪切带外部区域停止缩减，在土样表面形成连续完整的剪切破坏带状区域，此时剪切带完全形成.

延伸贯穿阶段(N5试验轴向位移7～12 mm)：在这一阶段，表面应变分布的跨越区间逐渐延伸，分布相对均匀，说明应变集中仍在加剧. 土样表面的剪切带停止扩张标志其完全形成，但随着试验进展，土样整体变形增大，应变局部化现象沿土样截面纵深继续发展，直至贯穿整个土样横截面. 其中6～9 mm之间有正值应变，追踪相应标记点，可知剪切带快速扩张，局部变形较为剧烈，导致橡皮膜与土样间相互滑移，于是出现正值应变.

相对滑移阶段(N5试验轴向位移13～14 mm)：这一阶段，应变分布的跨度陡然扩大，局部变形量在0.8%～17%之间均匀分布，土样表面变形量的差距达到最大. 应变的剧增标志着土样被剪切带彻底贯穿，土样整体分割为两个独立的斜切体. 此时，土样表面的较大应变主要来自于斜切体间的相对滑动，不再是土样自身的“应变”.

根据以上分析，土样剪切带发展的过程可区分为压缩变形、表面扩张、延伸贯穿、相对滑移四个阶段，据此选取各个阶段的土样变形实物图像进行对照，如图13所示. 可见土样呈现明显的阶段性递进破坏，实际剪切破坏情况与各个阶段的变形分析相符. 基于摄影测量的三轴试验能够监测剪切破坏全程的土样全表面变形，据此分析得到的剪切带演变规律准确可靠.

图13 不同轴向位移下剪切带四个发展阶段的土样变形. (a) 1 mm;(b) 6 mm; (c) 10 mm; (d) 14 mmFig.13 Deformation of soil samples in the four development stages of the shear band with different axial displacements: (a) 1 mm; (b) 6 mm;(c) 10 mm; (d) 14 mm

5 结论

本文运用摄影测量技术改良三轴试验，对土样变形破坏进行全程监测. 通过图像采集和计算机处理，获取了更精确的土样局部变形数据，得到了更可靠的本构关系和变形特征，实现了针对局部变形的定向研究. 据此，提出了基于表面应变判别剪切带发展阶段的方法，对应变局部化现象的演变过程进行了分析，为探索应变局部化现象提供了一种经济有效的研究方案. 具体结论如下：

(1)常规三轴试验测得的偏应力更大、应变更小，得到的强度偏大. 通过摄影测量技术直接采集的变形信息更为准确，测得土样中部区域不受端部约束影响，土体强度偏小.

(2)以剪切带为界划分土样表面，内外两个区域具有截然不同的变形特性. 带外区域变形较为均匀且变形量趋于稳定，带内区域发生不均匀变形且变形量不断加剧.

(3)在土样表面，剪切带内外区域的平均局部应变曲线发生分叉，标志着剪切带开始形成；剪切带在土样表面停止扩张，带外的表面局部变形量占比趋于不变，标志着剪切带完全形成；表面应变分布的跨度陡然扩大，说明土样应变剧增，标志着剪切带彻底贯穿土样.

(4)根据上述临界状态判别方法，提出根据表面局部应变区分剪切带发展阶段. 将剪切带的演化过程拆分为压缩变形、表面扩张、延伸贯穿、相对滑移四个阶段.