基于多目标粒子群优化的污水处理系统自适应评判控制
2024-04-12赵慧玲
王 鼎,赵慧玲,李 鑫
1) 北京工业大学信息学部,北京 100124 2) 计算智能与智能系统北京市重点实验室,北京 100124 3) 智慧环保北京实验室,北京 100124 4) 北京人工智能研究院,北京 100124
水资源短缺和水污染严重仍然是制约当今社会经济建设可持续发展的重要因素之一. 二十大报告中指出要深入推进环境污染防治, 持续深入打好蓝天、碧水、净土保卫战, 提升环境基础设施建设水平. 国家高度重视城市污水处理技术[1], 也出台了一系列水资源保护措施. 而气候变化、人口、基础设施老化等因素都将对城市污水处理系统管理造成重大压力. 城市污水管理部门亟需对污水处理工艺[2]进行优化. 污水处理系统本身是一个复杂的非线性系统[3], 目前我国城市污水处理厂最常用的有效工艺是活性污泥法[4], 在该工艺过程中, 生化反应的机理非常复杂, 各变量之间具有高度的非线性, 并且伴有大量的干扰,这使得污水处理机理模型难以精确建立. 对于传统的控制器设计, 由于自适应能力差、参数固定等原因, 难以达到理想的控制效果. 经过污水处理后的水质依然可能超标, 不符合国家的排放标准, 并且伴随着能耗大、运行成本高的问题. 所以在保证系统平稳运行的同时, 尽可能降低成本和提升水质一直是一个重要的研究课题. 因此, 设计自适应能力强的先进控制与优化方法, 是改善污水处理过程的关键突破点.
在污水处理过程中, 溶解氧和硝态氮浓度为两个关键控制变量, 其期望设定值一般都是根据人工经验设定的. 然而人工经验往往难以适应不同的工业情况, 并且很难对运行过程中的能耗和水质进行优化和均衡. 为解决这一问题, 学者们在污水处理关键变量的优化上做了很多研究. 根据优化目标的不同, 一般将优化问题分为单目标和多目标优化形式. 以降低能耗为优化目标, Åmand和Carlsson[5]利用线性规划算法实现了硝态氮浓度的动态优化设定, 该方法使得曝气能耗降低了14%. Duzinkiewicz等[6]设计了一种污水处理过程双层优化控制方法, 上层利用遗传算法优化能耗模型, 求解第五分区溶解氧的最优设定值, 下层利用模型预测控制实现对优化设定值的跟踪控制.为了处理污水处理厂多个冲突目标之间的权衡关系, 多目标优化控制被认为是一种很有前途的策略. Beraud等[7]利用多目标遗传算法和灵敏度分析法设计了污水处理过程的控制策略, 结果表明,采用多目标遗传算法的最优控制策略可以在提高系统出水水质的同时降低系统能耗. Sweetapple等[8]使用NSGA-II算法设计了一种最优控制策略, 为使用活性污泥工艺的污水处理厂推导出了一组最优设定值.
自适应动态规划(Adaptive dynamic programming,ADP)[9]结合动态规划[10]、强化学习[11]和神经网络[12],为求解最优控制问题提供了一种有效方案. 由于其强大的自适应能力和学习能力, ADP引起了学术界和工业界的广泛关注. 依托于ADP的理论[13-15],很多学者在调节器问题[16-17]、跟踪控制问题[18-19]等方面进行了广泛研究, ADP思想广泛地应用在了电力、智能家居、智慧交通、航空航天等各个领域.在文献[19-21]中, 不少学者将ADP思想用于解决污水处理过程关键变量的跟踪控制问题. 考虑到系统模型难以精确建立的情况, 充分利用数据驱动思想, Wang等[22]使用启发式动态规划技术实现了对污水处理过程中溶解氧和硝态氮浓度的跟踪控制. Liu等[23]为了控制和优化污水处理过程中溶解氧和硝态氮的浓度, 提出基于迭代ADP算法的污水处理优化控制策略, 实现对污水处理过程的控制和优化. Bo和Qiao[24]利用回声状态网络作为ADP方法中代价函数和控制策略的逼近器, 实现了关键浓度变量的在线控制. Yang等[25]利用经验回放技术, 设计了基于动态优先级策略梯度的ADP算法, 该方案在不依赖模型的情况下, 大大提高了污水处理系统的抗干扰能力.
受以上研究的启发, 本文提出一种基于多目标粒子群优化(Multi-objective particle swarm optimization, MOPSO)算法[26]的污水处理自适应评判控制方案. 首先, 对污水处理过程的入水及出水组分数据进行分析, 构建关于能耗和水质的优化目标函数模型. 接下来, 在优化过程中考虑了部分参数会随着时间进行动态更新, 采用MOPSO算法求解能够使目标函数最优的溶解氧与硝态氮浓度设定值. 考虑到比例–积分–微分(Proportional–Integral–Derivative, PID)控制具有其本身的优势, 且一般工业系统中的PID控制设备较难拆除, 所以底层跟踪控制部分设计了一个基于ADP的辅助控制器对PID得出的控制策略进行补充. 将以上算法应用于活性污泥污水处理基准仿真平台(Benchmark simulation model No.1, BSM1)上进行实验, 该模型可以评价污水处理过程控制策略的性能, 结果证明了该方法可以进一步提高污水处理过程的运行性能.
在本文中, R是所有实数的集合. Rn是所有n维实向量组成的欧氏空间. In是n×n维的单位矩阵.N代表所有非负整数的集合, 即{0,1,2,···}. 上标“T”代表转置操作.
1 污水处理过程分析
本文所有研究均是基于欧盟科学技术合作组织和国际水协合作组织联合开发的BSM1上进行的. 该模型为验证污水处理优化控制所设计的方法和策略是否有效提供了一个较为理想的平台,该模型一共包含两部分, 分别是生化反应池和二沉池. 其中生化反应池有五个分区, 前面两个分区为厌氧区, 后面三个分区为好氧区, 污水经过生化反应池中一系列硝化和反硝化反应之后, 进入到二沉池进行沉淀, 分离出的污泥直接排放出去或者是作为生化反应载体回流至厌氧区, 二沉池分离出的水可直接排出. 在生化反应池中, 位于好氧区第五分区的溶解氧浓度和厌氧区第二分区的硝态氮浓度很大程度上影响着污水处理过程的除氮效果, 所以设计良好的优化算法使得污水处理过程在实现水质达标的前提下尽量降低能耗, 并对溶解氧和硝态氮的浓度进行有效地跟踪控制使其保持在理想的设定点, 已经成为污水处理系统需要解决的问题.
1.1 污水处理过程能耗和水质
在设计优化算法之前, 先对污水处理过程中的能耗和水质模型进行分析, 其中能耗主要分为泵送能耗和曝气能耗, 泵送能耗(PE(t))的计算方式如下所示:
其中, τ为计算间隔,Qa(t)为t时刻的内回流量, 也是硝态氮浓度的控制量,Qr(t)为t时刻的外回流量,Qw(t)为t时刻的污泥排放量.
曝气能耗(AE(t))的计算方式为:
其中,SO,sat为溶解氧的饱和浓度,Vi为第i个反应池的体积,KLa,i(t)为t时刻第i个反应池的氧传递系数,KLa,5(t)是溶解氧浓度的控制量. 能耗(EC(t))可以表示为泵送能耗和曝气能耗的一个累加, 即
在BSM1中, 出水水质未达标需要支付一定的罚款, 这也会增加污水处理厂的运行成本, 水质指标(EQ(t))的计算表达式如下所示:
其中, SS(t)为固体悬浮物浓度, COD(t)为化学需氧量,SNO(t)为硝态氮浓度,SNkj(t)为凯氏氮浓度,BOD(t)为生化需氧量,Qe(t)为出水流量. 同时在污水处理过程中, BSM1对一些组分浓度也有一定的限制, 例如总氮质量浓度Ntot<18mg·L-1, 氨氮质量浓度SNH<4mg·L-1. 第五分区的溶解氧质量浓度SO,5(t)和第二分区的硝态氮质量浓度SNO,2(t)的变化很大程度上会影响Ntot和SNH, 从而影响水质.由于溶解氧和硝态氮浓度过高过低都会对污水处理过程产生影响, 溶解氧浓度过低会导致污泥膨胀、影响出水水质, 过高会导致系统运行能耗增加. 硝态氮浓度过低会导致有机物不能彻底被降解, 过高会导致水体富营养化, 所以应对这两个关键变量进行约束, 其约束规则为
综上所述溶解氧浓度和硝态氮浓度是关系到能耗和水质的关键因素.
1.2 污水处理优化控制过程
运行能耗和出水水质是污水处理过程中两个重要的评价指标, 用于表征污水处理过程运行成本及向水体排放污染物超标引起的罚款, 所以我们可以将污水处理的设定值优化问题理解为一个多目标优化问题. 一般的多目标优化问题可以描述为
其中,t为时间变量,x为决策变量,f(x,t)为优化目标函数, ϑ为优化空间维度,yι(x,t)和hν(x,t)分别表示不等式约束和等式约束条件. 这里考虑污水运行过程的实际情况, 优化目标定义为运行过程产生的能耗和出水水质, 优化空间维度为二维, 决策变量为溶解氧与硝态氮的质量浓度, 不等式约束条件如式(5)所示.污水处理过程的优化控制方案根据层级结构分为两部分, 上层为优化过程, 根据污水处理的运行过程构造优化目标函数, 并通过智能优化算法求解优化后的设定值. 底层为溶解氧与硝态氮浓度的跟踪控制过程, 设计控制器来跟踪上层的优化设定值, 实现污水处理的闭环优化控制. 首先,利用数据驱动的思想, 设计优化目标模型来表示优化目标与输入变量之间的关系. 其次, 在上层优化阶段采用MOPSO算法, 求解使优化目标函数最小化的设定值. 最后, 采用基于ADP的辅助控制器对PID控制策略进行补充, 从而跟踪SO,5(t)和SNO,2(t)的最优设定值. 接下来, 对此框架的多目标优化过程及底层跟踪控制过程进行详细的分析.
2 多目标优化过程
2.1 构建优化目标函数模型
污水处理过程本身具有很强的非线性、时变性等特点, 而能耗和出水水质机理模型, 其模型参数固定不变, 无法根据污水处理过程的实际情况进行自适应变化. 为了模拟污水处理过程中的动态特性, 需要利用数据驱动的思想对其进行建模,首先根据污水处理运行特点及运行数据来分析与能耗和出水水质相关的过程变量, 然后利用径向基函数(Radial basis function, RBF)神经网络建立能耗和出水水质与过程变量之间的模型.
在式(1)中,Qa(t)、Qw(t)、Qr(t)三个变量共同影响着PE(t), 但在实际运行过程中,Qw(t)和Qr(t)的变化幅度很小, 对PE(t)的影响也微乎其微, 可以将其考虑为静态量, 则与PE(t)直接相关的只有内回流量Qa(t). 在式(2)中,SO,sat和Vi保持不变, 则与AE(t)直接相关的变量为KLa,i(t), 在生化池第五单元中,KLa,5(t)为SO,5(t)的控制量. EQ(t)由SS(t)、COD(t)、SNO(t)、SNkj(t)、BOD(t)、Qe(t)共同决定. 选择EC(t)、EQ(t)作为模型的输出, 优化目标函数模型可以表示为
其中, EC(s(t))和EQ(s(t))分别为能耗模型和出水水质模型,s(t)为输入变量, 其形式定义为
在建模之前, 为提高模型训练的性能, 需要对数据进行归一化处理, 归一化后的输入变量s′(t)表示为
其中,smin表示由最小元素组成的输入变量下界,smax表示由最大元素组成的输入变量上界,在得到输出结果后还需对结果进行反归一化.
这里采用RBF神经网络对能耗和水质进行建模, 其网络拓扑结构如图1所示.
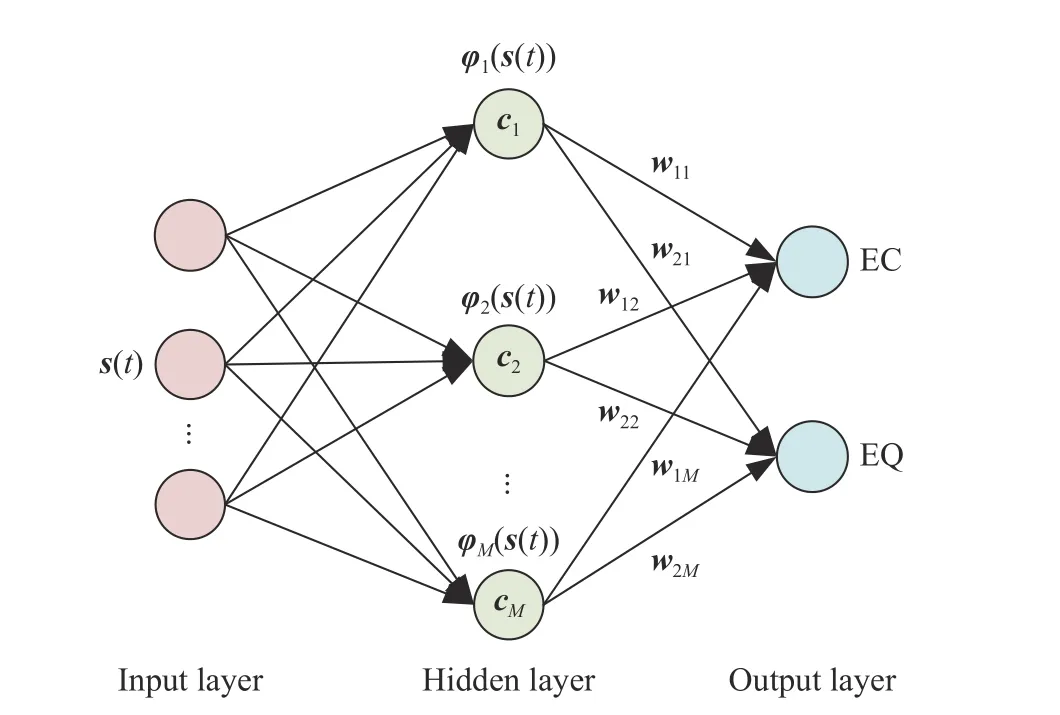
图1 RBF神经网络拓扑结构Fig.1 Topology of the RBF neural network
能耗和水质的模型表达式为
其中,w1m和w2m为权值向量, φ(·)为径向基函数, 也是隐含层的激活函数,M为隐含层神经元的个数,这里选取如下的高斯函数作为径向基函数:
其中,cm为第m个基函数的中心值, σm为第m个基函数中心的宽度.
2.2 优化设定值求解
为了同时满足降低能耗和提高出水水质的要求, 我们采用MOPSO算法来求解溶解氧和硝态氮浓度的优化设定值. MOPSO是一种基于群体的优化算法, 其中粒子之间能够相互交流信息, 从而进行协作行为. 每个粒子都有一个表示其在搜索空间中坐标的位置向量, 并使用速度向量更新位置向量. 第i个粒子的位置信息可以定义为
其中,k为迭代指标,i=1,2,···,H,H为粒子种群的个体数量,D是粒子的探索空间维数. 粒子的速度可以表示为
粒子速度和位置的更新规则如下所示:
其中,d表示搜索空间中的第d维, ϖ为惯性权值,rand为(0, 1)之间的随机值,pdi(k)为第k步迭代的个体最优值,gdi(k)为第k步迭代的全局最优值,κ1和κ2分别为个体学习系数和全局学习系数. 个体最优解的获得遵循以下原则:
其中,xi(k)≺pi(k-1)的意思是xi(k)不受pi(k-1)的支配. 另外定义一个存储库A进行实时更新以存储非支配粒子a, 其更新规则为
其中,A(k)=[a1(k),a2(k),···,aG(k)]T是第k次迭代的存储库,G为存储库的大小,A¯(k-1)是第k-1次迭代中去掉了被支配的冗余值之后的存储库,ai(k-1)≺≻pi(k-1)表示两者互相不能支配对方. MOPSO的运动过程将不断重复, 直到满足某些终止条件, 其算法过程如图2所示, 其中,p(k)为全部粒子,p_best为个体最优值,g_best为全局最优值.
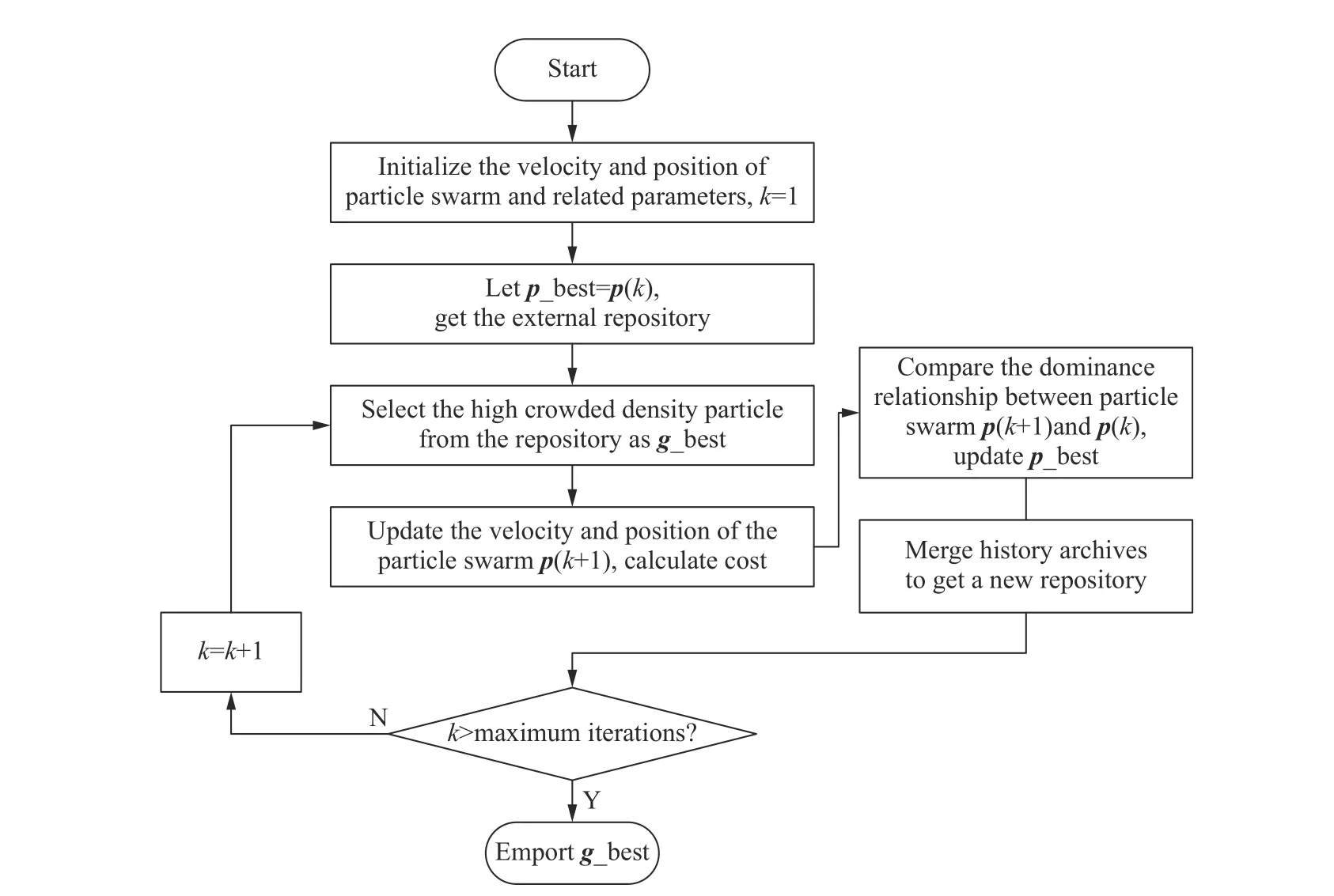
图2 多目标优化过程Fig.2 Multiobjective optimization process
3 底层跟踪控制器设计
在底层跟踪控制阶段, 一般采用增量式PID控制来跟踪溶解氧和硝态氮浓度的设定值, 控制律uo(t)可以表示为
其中
其中,e(t)表示跟踪误差,Kp、Ki和Kd分别表示PID控制中的比例系数矩阵、积分系数矩阵和微分系数矩阵. 由于原始的控制器也具备一定的优越性,且对于污水处理系统PID控制器的设备较难拆除,因此在不改变原控制器的情况下, 设计一个基于ADP算法的辅助控制器对控制律进行补充.
污水处理系统是一个典型的非仿射非线性系统, 其离散形式可以表示为
其中,x(t)∈Rn是状态变量,u(t)∈Rm是原始系统的控制输入. 系统函数F(·,·)关于其自变量是可微的.参考轨迹可以表示为r(t+1)=Γ(r(t)). 跟踪误差为系统状态与参考轨迹的差值e(t)=x(t)-r(t), 假设系统(21)存在一个原控制律uo(t)可以使系统稳定,但其性能有待进一步提高. 添加一个补充控制律us(t)来对原控制律进行调整, 则最终的控制律可以表示为
误差系统可以表示为
将效用函数定义为关于误差与补充控制律二次型的形式, 如下所示:
代价函数定义为
为了表达简洁, 将J(e(t),us(t))表示为J(t). 设计控制器的目的是找到一个最优的控制律保证系统(21)稳定的同时使代价函数最小化, 根据Bellman最优性原理, 最优的代价函数可以表示为
最优的补充控制律可以通过下式得到
接下来, 构建评判网络用来近似代价函数, 执行网络用来产生补充控制信号以提高PID控制器的控制性能.
3.1 评判网络
采用以下函数近似结构来逼近代价函数
其中, ωc1(t)和ωc2(t)分别为评判网络输入层与隐含层之间和隐含层与输出层之间的权值, δ(·)为激活函数, 这里选取双曲正切函数作为激活函数. 损失函数可以定义为
性能指标函数可以定义为
这里只对隐含层与输出层之间的权值进行更新, 其更新规则如下式所示:
其中, αc表示评判网络的学习率.
3.2 执行网络
构建执行网络用于近似补充控制律, 其表达式为
其中, ωa1(t)和ωa2(t)分别为执行网络输入层与隐含层之间和隐含层与输出层之间的权值, δ(·)为与评判网络一致的激活函数, 执行网络的损失函数为
误差性能指标函数为
隐含层与输出层之间的权值更新规则可以表示为
其中, αa表示执行网络的学习率.
4 仿真研究
整体的优化控制框架如图3所示. 针对晴天天气下的污水流量和组分数据, 在BSM1上对本文所提算法进行实验验证, 模拟时间为14 d, 每次采样间隔为15 min, 优化周期为2 h. 两个操作变量是KLa,5(t)和Qa(t).
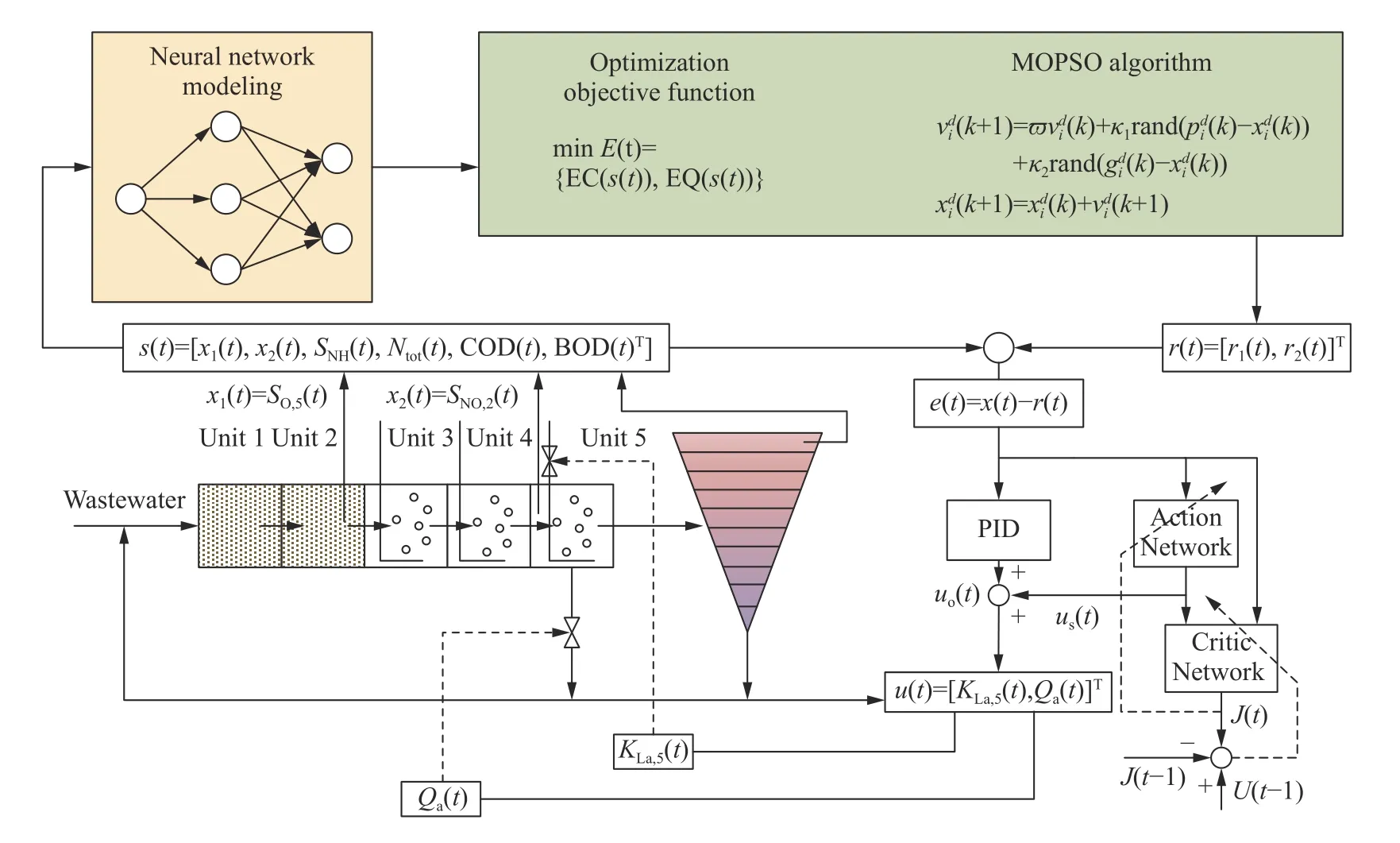
图3 污水处理过程优化控制整体框架Fig.3 Overall framework for the optimization and control of a wastewater treatment process
首先基于入水与出水组分数据对能耗和水质进行建模, 取1000组数据作为训练样本, 采用RBF神经网络进行建模, 其中隐含层神经元个数M=8.取344组数据作为测试样本, 将最终的预测效果与BP神经网络进行了对比, 从图4和图5能耗和水质模型的预测效果,图6和图7给出了模型的预测误差, 基于RBF模型的预测效果明显优于BP神经网络的预测效果.
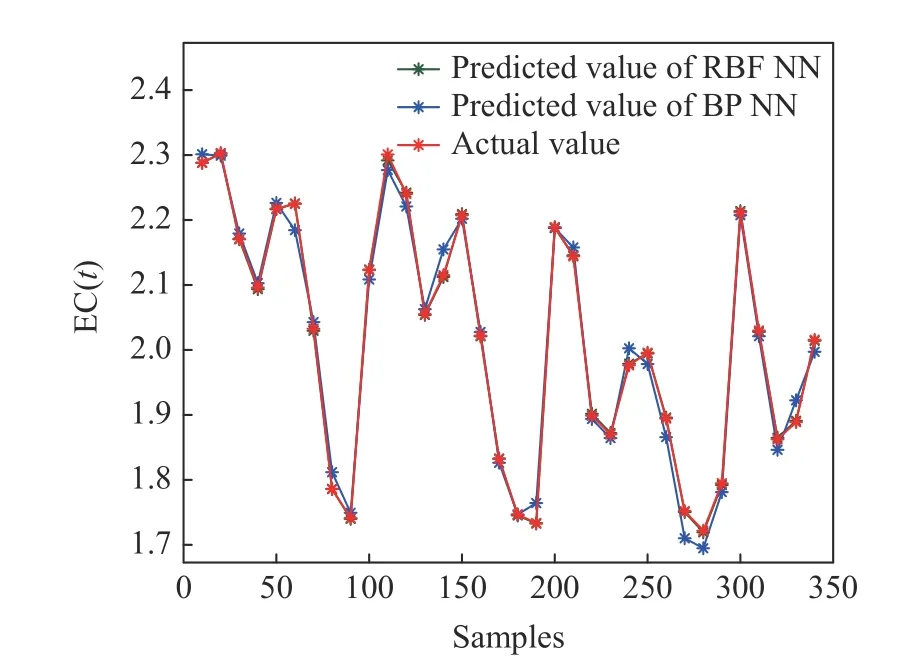
图4 运行能耗预测效果Fig.4 Prediction effect of the energy consumption
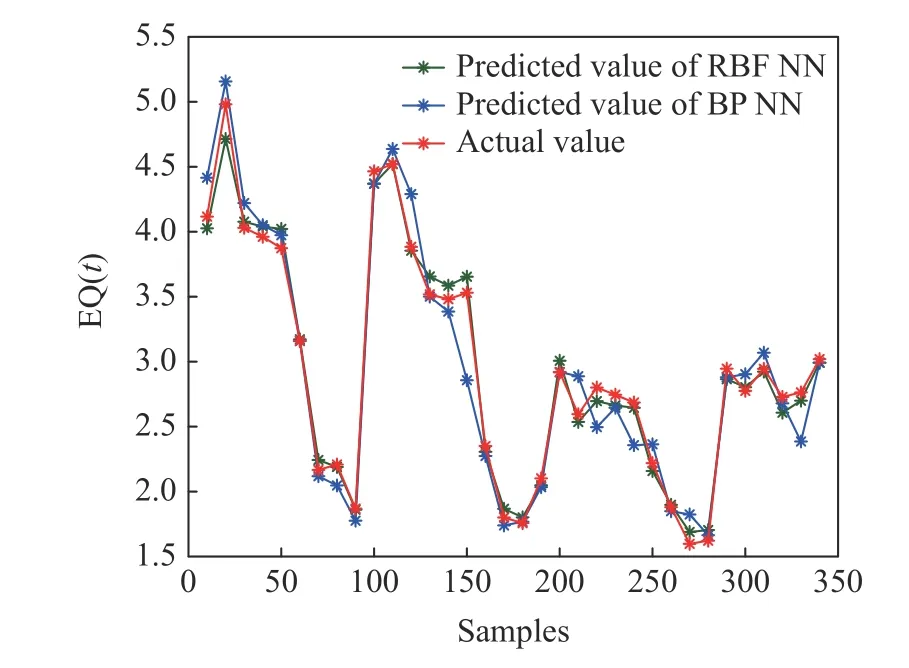
图5 出水水质预测效果Fig.5 Prediction effect of the effluent quality
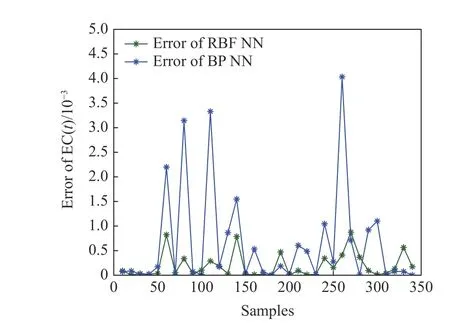
图6 运行能耗预测误差Fig.6 Prediction error of the energy consumption
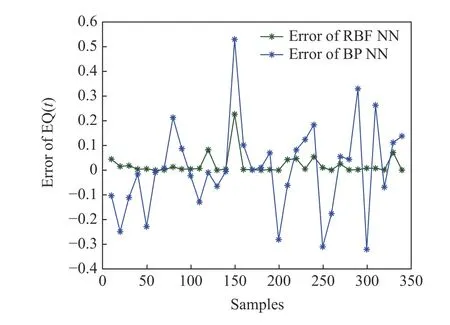
图7 出水水质预测误差Fig.7 Prediction error of the effluent quality
接下来, 基于建立好的污水处理能耗和水质模型, 采用MOPSO算法求解最优设定值, 其中, 种群规模、粒子的探索空间维数、个体学习系数、全局学习系数和惯性权值均在表1中给出.

表1 多目标优化算法的参数值Table 1 Parameter values of the multiobjective optimization algorithm
这里粒子搜索空间为二维, 决策变量为x(t)=[SO,5(t),SNO,2(t)]T. 选择一组入水组分数据作为实验样例进行展示, 经过100次的迭代计算, 对能耗和出水水质目标进行优化, 图8展示了能耗与水质两个目标优化的最优解集.

图8 多目标优化结果Fig.8 Results of the multiobjective optimization algorithm
从图中可以看出, 在这一组寻优的Pareto最优解集中, 反映出污水处理过程中的两个重要指标—能耗和出水水质呈现出一种相互制约的关系. 这与实际生产是一致的, 水质和运行能耗是一对不可兼得的目标, 提高出水水质质量势必要以增加能耗为代价, 因此需要对这两者进行一个平衡的取舍. 一般能耗和水质存在一定的偏好关系,本文将优化目标函数E(t)定义为
根据上式对最优解进行决策.将通过以上决策规则选出的最优解设定为底层跟踪系统的参考输入, 采用基于ADP算法的辅助控制器来补充PID得到的控制策略, 评判网络和执行网络的结构为4–8–1、2–8–2. PID控制器的参数以及ADP控制器的相关参数均在表2中给出.

表2 底层跟踪控制算法参数值Table 2 Parameter values of the underlying tracking control algorithm
图9 和图10分别展示了晴天天气下对污水处理系统进行优化后的溶解氧和硝态氮浓度设定值及其跟踪效果. 从图中我们可以看到本文所提辅助控制器能够将溶解氧和硝态氮浓度的实际值与设定值的差值控制在比较好的范围内. 结果表明基于ADP的辅助控制器能够对PID产生的控制策略进行补充, 实现较好的跟踪控制性能.
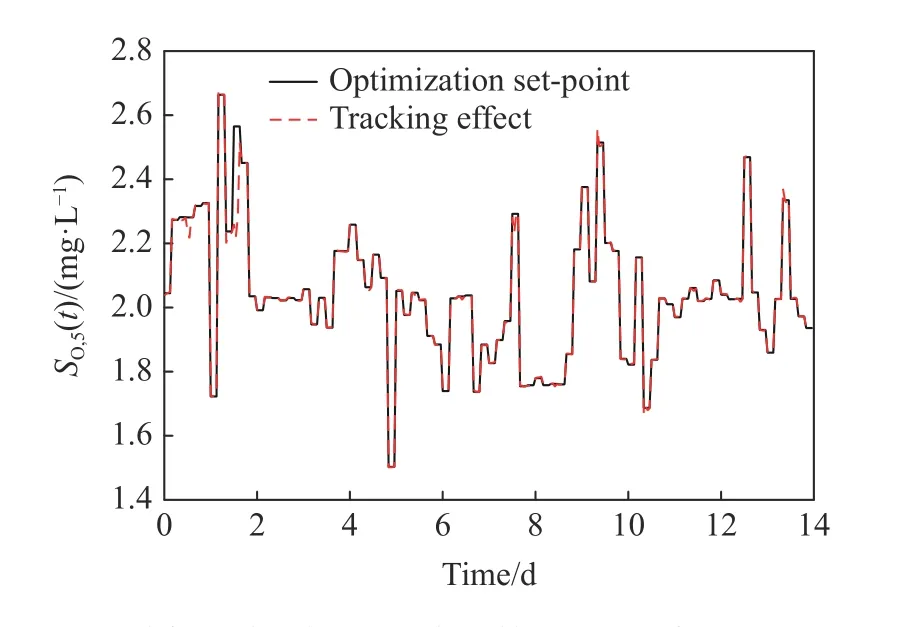
图9 溶解氧浓度的优化结果及跟踪效果Fig.9 Optimization result and tracking effect of dissolved oxygen concentration
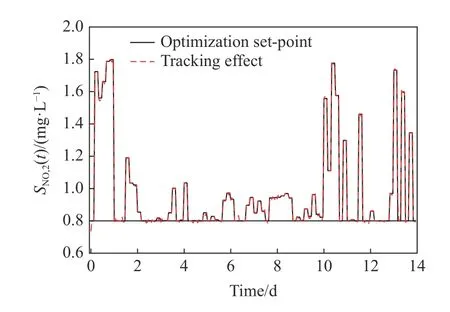
图10 硝态氮浓度的优化结果及跟踪效果Fig.10 Optimization result and tracking effect of nitrate nitrogen concentration
为了进一步说明本文所提优化控制算法的优越性, 针对不同算法获得的平均氨氮浓度、平均总氮浓度、平均生化需氧量、平均化学需氧量、平均能耗和平均出水质进行了比较, 对比结果在表3中给出. 结果表明, 本文所提算法可以通过获取动态优化设定值, 有效降低能耗, 提高出水水质.

表3 不同优化控制策略的比较结果Table 3 Comparison results of different optimal control strategies
5 结论
针对污水处理过程的多目标优化控制问题,本文提出了一种基于MOPSO算法的自适应评判优化控制方案. 通过对入水及出水组分的相关数据进行分析, 采用RBF神经网络构建了关于出水水质和运行能耗的优化目标模型. 利用MOPSO算法对能耗和水质的多目标优化函数进行求解, 并设计一个决策方式进行两个优化目标的均衡, 从Pareto最优解集中选出溶解氧与硝态氮浓度的最优设定值. 接下来, 采用一个基于ADP的辅助控制器对PID控制器的控制策略进行补充, 实现对最优设定值的跟踪控制. 所提算法在BSM1上进行了验证, 结果表明本文所提优化控制方案能有效地提高污水处理过程的运行性能.
