碎石土路基填料压实及渗透特性

2024-04-12李慎刚石云方刘晋宁

工程科学学报 2024年5期

李慎刚，石云方，刘晋宁，蒋琛

东北大学资源与土木工程学院，沈阳 110891

碎石土是一种由碎石和细粒土组成的土石混合体. 其在路基工程施工场地附近大量存在，可以快速就地取材充当路基填料广泛应用于路基工程，有利于资源的开发和原位利用，提高工程经济性. 路基作为主要受力结构，其强度、刚度及变形特性直接影响上部结构的运营效果，路基压实度是路基建设的重要指标. 碎石土作为路基填料时，块石在路基压实过程中相互接触、挤压，不断破碎形成较小的颗粒，碎石土级配产生变化，进而影响后续压实及运营过程中的工程特性. 决定路基使用性能的是经过压实后的填料，而非前期级配. 因此，研究碎石土压实破碎特性对工程实践具有重要意义. 目前已有大量学者采用大型直剪试验[1-2]、大型三轴试验[3-4]、击实试验[5]等对不同级配、多种影响因素下土石混合体破碎性能进行了研究分析. 同时，作为路基填料，不可避免的会受到降雨渗透的影响，降雨入渗会带走路基中的细颗粒导致路基使用性能下降，甚至发生边坡破坏[6].

分形理论自Mandelbrot创建以来早已广泛应用于自然科学. 谢和平等[7]在将其应用在岩土材料中. 近年来，大量学者应用分形理论对岩土材料进行分析，均表明分形维数与岩土材料的性能有良好的相关性. 刘新荣等[8]利用分形几何学的统计规律得到土石混合体剪切面上的颗粒相互作用规律. Su等[9]通过分形理论提出了多孔介质渗透特性的预测模型. 压实过程中碎石破碎是影响碎石土性能的主要因素. Chen等[10]对碎石土强夯过程中的破碎特性研究，指出碎石的破碎会影响碎石土的力学特性，并针对其破碎特性提出了修正本构模型. Cui等[11]通过模拟对比真实试验结果，指出考虑颗粒破碎时模拟结果更符合试验结果.Xu[12-13]通过统计分析前人试验数据，得出脆性颗粒破碎分维与施加应力的关系，又通过试验提出可以采用分形维数作为压实度的指标. 王启云等[14-15]对粗颗粒破碎演化过程进行了研究，并借助分形维数描述了冲击荷载下粗颗粒的破碎演化过程的级配方程. Li等[16]提出利用破碎分形对路基填料进行的级配进行分析. 研究表明，分形理论能够良好的描述不同级配填料的破碎、渗透特性. 为此，本文通过配置不同级配的碎石土进行击实及渗透试验，重点考虑不同级配下碎石土的冲击、渗透等因素对碎石土级配的影响，分析填料的破碎、侵蚀特征，为碎石土应用于路基填料的性能提供参考.

1 实验方案

1.1 试验材料及实验装置

本文依托吉林省某路基工程项目，碎石土试样取自施工场地，其中碎石材料棱角分明，经点荷载试验测定，无侧限抗压强度RC约60 MPa，为硬岩. 经筛分确定细颗粒中粒径大于0.075 mm的颗粒质量分数超过50%，属于砂类土. 采用LP-100D数显式土壤液塑限联合测定仪进行测定，细颗粒液限23，塑限9.6，根据《公路土工试验规程》[17]确定为砂类土. 参考试验[18-19]，本实验采用最大孔径为19 mm的标准方孔筛对碎石土试样进行筛分，采用5 mm作为土、石的分界标准，试样如图1所示.

图1 碎石土试样. (a) 碎石(粒径5～20 mm颗粒); (b) 细粒土(粒径＜5 mm颗粒)Fig.1 Gravel soil sample: (a) gravel (particle size 5–20mm); (b) soil (particle size＜5 mm)

击实试验按照《公路土工试验规程》[17]的要求，采用小击实筒，试样直径10 cm，高度约12.7 cm，击实及渗透装置采用自制的组合式击实渗透试验筒，可对压实后试样进行原位渗透试验，减小试样移动造成的误差.

1.2 击实试验方案

击实试验采用重型击实方案，使用4.5 kg击锤进行，落高450 mm，分3层击实，每层击实27次.参考文献[20-21]及前期试验预设3个含石量分别为50%、60%、70%，预设4个含水质量分数（简称含水率）分别为6%、8%、10%、12%，分组情况如表1所示.

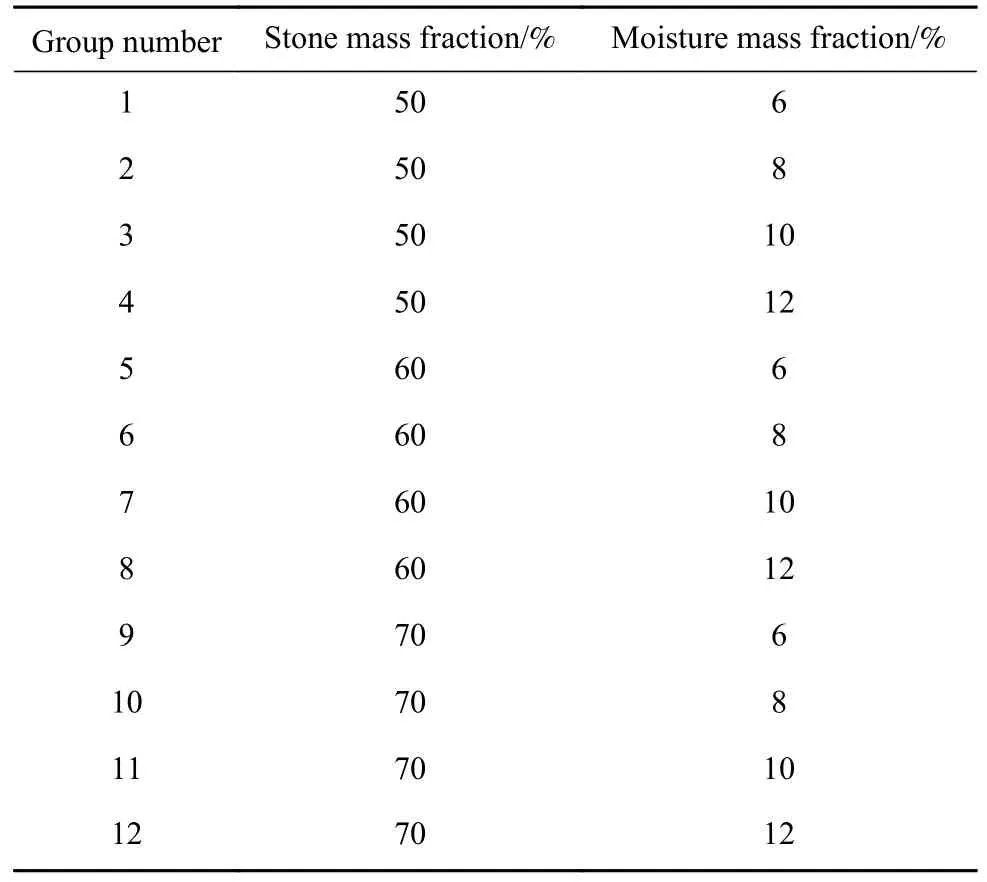
表1 试验分组Table 1 Test groups

为减小试验误差，每组试样制样6份，分别取3份进行击实试验和击实后的渗透试验. 在击实和渗透试验后，将试样烘干，进行筛分，测定击实后试样的颗粒级配，最后取每组试样的平均值进行分析.

1.3 渗透试验方案

取击实并饱和后的试样采用常水头试验方案进行，渗透装置如图2所示，自进水盒上方加水，超出进水盒高度的水自然溢出，保持水面高度为进水盒高度，进水盒高度50 mm，水压约500 Pa，采用公式(1)计算渗透系数.

图2 渗透试验装置Fig.2 Penetration testing device

式中，k为渗透系数，cm·s–1；A为试样截面积，为78.5 cm2；L为渗径即试样高度，mm；Q为t时间内总渗透水量，cm3；h为常水头，本试验中为15 cm；t为渗透时间，本实验中每60 s记录一次，共记录6次.

2 实验结果及分析

2.1 击实试验

对各组配比进行击实试验，取各组击实后的平均干密度，结果如图3所示.

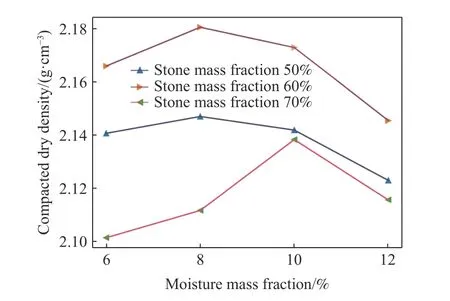
图3 不同配比试样的击实干密度Fig.3 Compacted dry density of samples for different proportions

从图3中可以看出，含石量50%和60%的变化规律相近，均在含水率8%附近达到最大干密度，但含石量60%压实密度较高. 当含水率超过10%时，试样的干密度明显下降，其主要原因是碎石土中的水主要存在于细颗粒之间，此时含水率已接近液限，细颗粒在击实过程中会产生滑移影响压实效果. 而含石量70%时在含水率10%时达到最大干密度，其原因可能是此时在压实的过程中碎石破碎程度更高，更好的填充了碎石之间的空隙，进而达到了较高的干密度.

2.2 渗透试验

对击实后试样进行常水头试验，按公式(1)计算得到渗透系数，结果如图4所示.

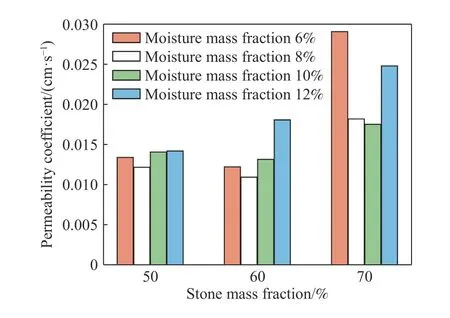
图4 不同配比试样的渗透系数Fig.4 Permeability coefficient of samples for different proportions

从图4可以看出，渗透系数在0.01～0.03 cm·s–1之间，变化趋势与干密度相反，分析这主要是试样的干密度越大表示试样的密实度越高，试样内部供液体流动的贯通孔隙就越少，进而导致渗透系数变小，反之干密度越小则密实度越低，贯通孔隙越多，渗透系数就越大. 从总体来看除含石量70%以外，各配比试样的渗透系数相近，对实际渗透效果的影响较小.

3 颗粒破碎及侵蚀特征

3.1 击实试验后试样颗粒破碎特征

采用标准方孔筛对击实前后的不同配比试样进行筛分，得到累计颗粒分布曲线如图5所示.

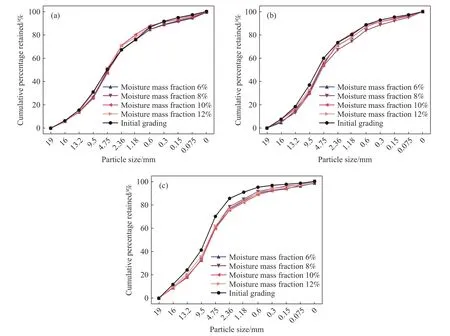
图5 累计颗粒分布曲线. (a)含石质量分数50%; (b)含石质量分数60%; (c)含石质量分数70%Fig.5 Cumulative particle distribution curve: (a) stone mass fraction 50%; (b) stone mass fraction 60%; (c) stone mass fraction 70%

由图5可以看出，同一含石量下，含水率对颗粒含量变化的影响较小，因此将同一含石量的颗粒含量变化量取平均值，通过计算得到不同含石量各粒组平均颗粒含量变化情况如图6所示，图中正值表示含量增加，负值表示含量减少. 其中，由于粗颗粒在9.5～19 mm粒径范围内均呈现减少趋势，但击实过程中颗粒破碎带来的质量变化表现出较大的随机性，因此此处仅选择了dmax/2 (即9.5 mm)作为粗颗粒控制粒径进行含量变化计算和分析.

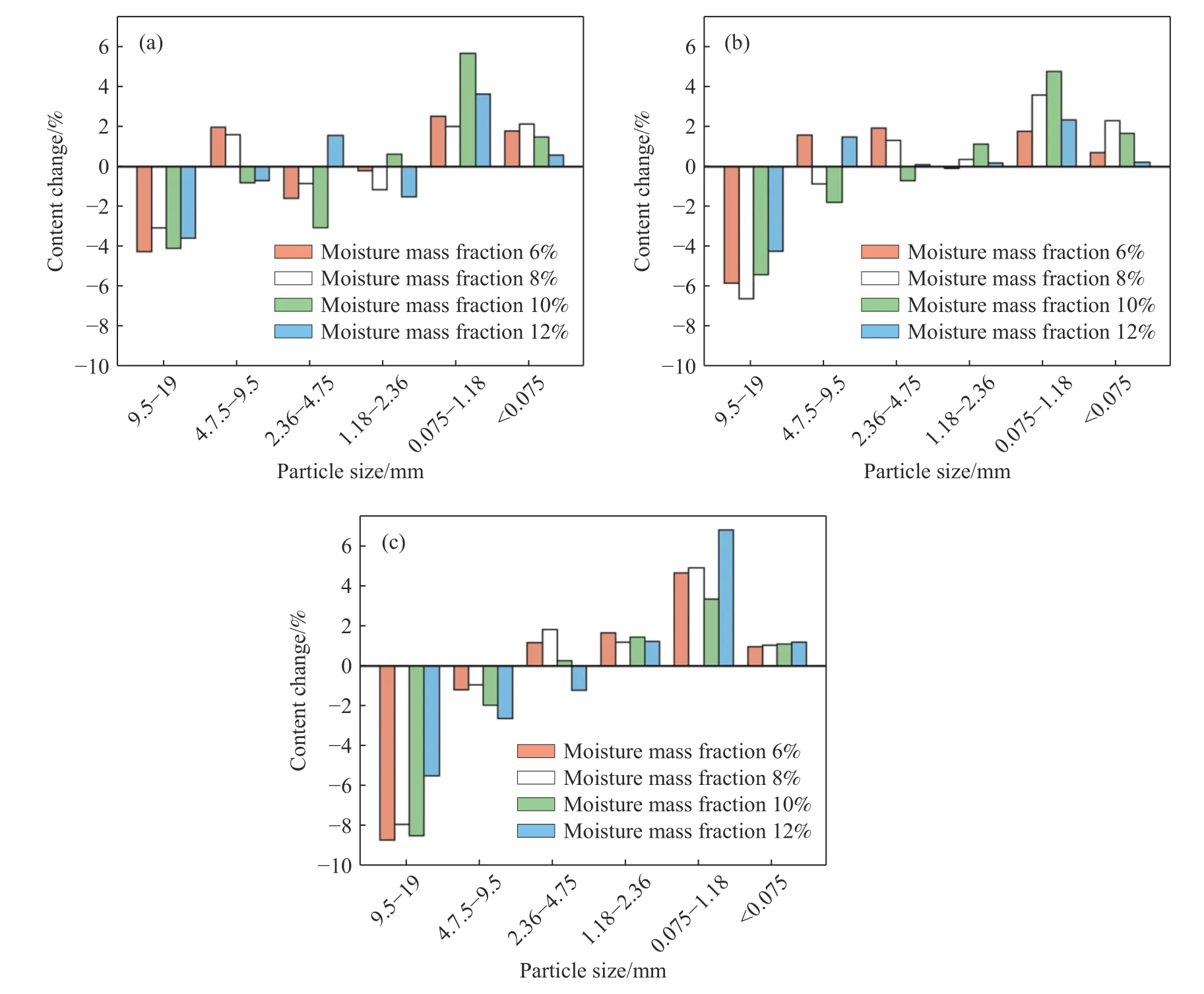
图6 击实前后颗粒含量变化. (a)含石质量分数50%; (b)含石质量分数60%; (c)含石质量分数70%Fig.6 Particle content change before and after compaction: (a) stone mass fraction 50%; (b) stone mass fraction 60%; (c) stone mass fraction 70%

从图6可以看出，击实前后各含石量的颗粒含量变化规律基本一致. 粒径在9.5～19 mm的颗粒含量分别减少2%～4%、2%～6%、5%～10%，减小幅度与含石量相关；4.75～9.5 mm的颗粒变化程度不同，当含石量达到70%时，该粒径范围颗粒含量均出现减小，而对于含石量50%和60%的试样，该范围颗粒含量也可能增加表明在击实过程中该粒组颗粒也会发生破碎，而9.5～19 mm颗粒的破碎会补充该粒组的含量，但4.75～19 mm粒径的含量变化总体是减小的，减小幅度在2%～8%之间.4.75 mm粒径以下颗粒含量整体明显增加，在最优含水率处可以达到10%左右.

同时，从图4可以看出，当含水率超过最优含水率时，粒径在0.075 mm以下的颗粒增加量明显减小，这是由于颗粒破碎主要分为破裂、破碎和研磨3种方式[22]，细颗粒主要由研磨产生，水在击实过程中主要起到降低摩擦[23]和弱化强度[24]两方面的作用. 本实验采用的硬岩强度较高，碎石受水作用弱化强度后仍能保持较高的强度，在击实过程中，水对碎石破碎的影响较小，而研磨现象主要由碎石之间的摩擦产生，含水率会显著影响碎石之间的摩擦力，含水率高时，碎石之间的摩擦力减小，研磨产生的细颗粒相对减少. 这种变化规律在不同级配的试样中变化规律相近，说明在击实过程中是具有代表性的.

为了更好地分析击实前后颗粒破碎特征，本文引入Marsal[25]提出的破碎率Bg对击实试验造成的颗粒破碎情况进一步分析，其定义如式(2)所示.

式中，Wki表示击实试验前级配曲线中某级粒组的百分含量；Wkf表示击实试验后级配曲线中某级粒组的百分含量.

在本文中破碎率Bg表示了击实试验前各粒组的质量分数减去对应粒组的质量分数的绝对值之和，本实验各配比试样的破碎率如表2所示.

表2 不同配比的破碎率Table 2 Crushing rate of different proportions

从表2中可以看出，整体上同一含石量呈现出在破碎率较高时达到更大的干密度，但过高的破碎率也不利用试样的压实这主要因为破碎率越高，压实破碎导致的粗颗粒减少、细颗粒增加的幅度越大，破碎产生的细颗粒可以更好的填充碎石之间的空隙. 但对比不同含石量的破碎率可以看出，过高或过低的破碎率都是不利于击实效果的，这是因为在一定的击实功作用下，破碎是有一定限度的[26]，达到破碎极限后仍会有碎石形成空隙，过高的破碎率在一定程度上反映出含石量是不合理的.

3.2 颗粒破碎分形分析

为表征击实后碎石土的破碎状态，根据分形几何中的质量–等效尺寸关系[27]，采用描述散体状态的式(3)计算分形维数D来对粗颗粒发生破碎的程度进行分析[28].

式中，y为破碎程度；MR为颗粒尺寸小于di的总质量；MT为颗粒总质量；dmax表示最大粒径；D为分形维数.

由于质量–等效尺寸关系基于Tyler与Wheatcraft提出的颗粒具有相同密度的假设[27]，而本实验中粗细颗粒之间密度有较大差距，但粗细颗粒分别具有密度相近的特点，同时击实过程中发生破碎现象以粗颗粒体积减小，细颗粒体积增加为主. 因此本文对分形维数的讨论以5 mm为界限进行研究，并将式(3)取对数，进一步改写为式(4)和(5)：

式中，D20与D5分别表示粗颗粒和细颗粒的分形维数；M20与M5分别表示粒径小于20、5 mm的颗粒总质量.

根据不同配比情况拟合如图7所示分形维数与含石量、含水率的关系曲线，并计算分形维数及其相关系数汇总如表3所示.

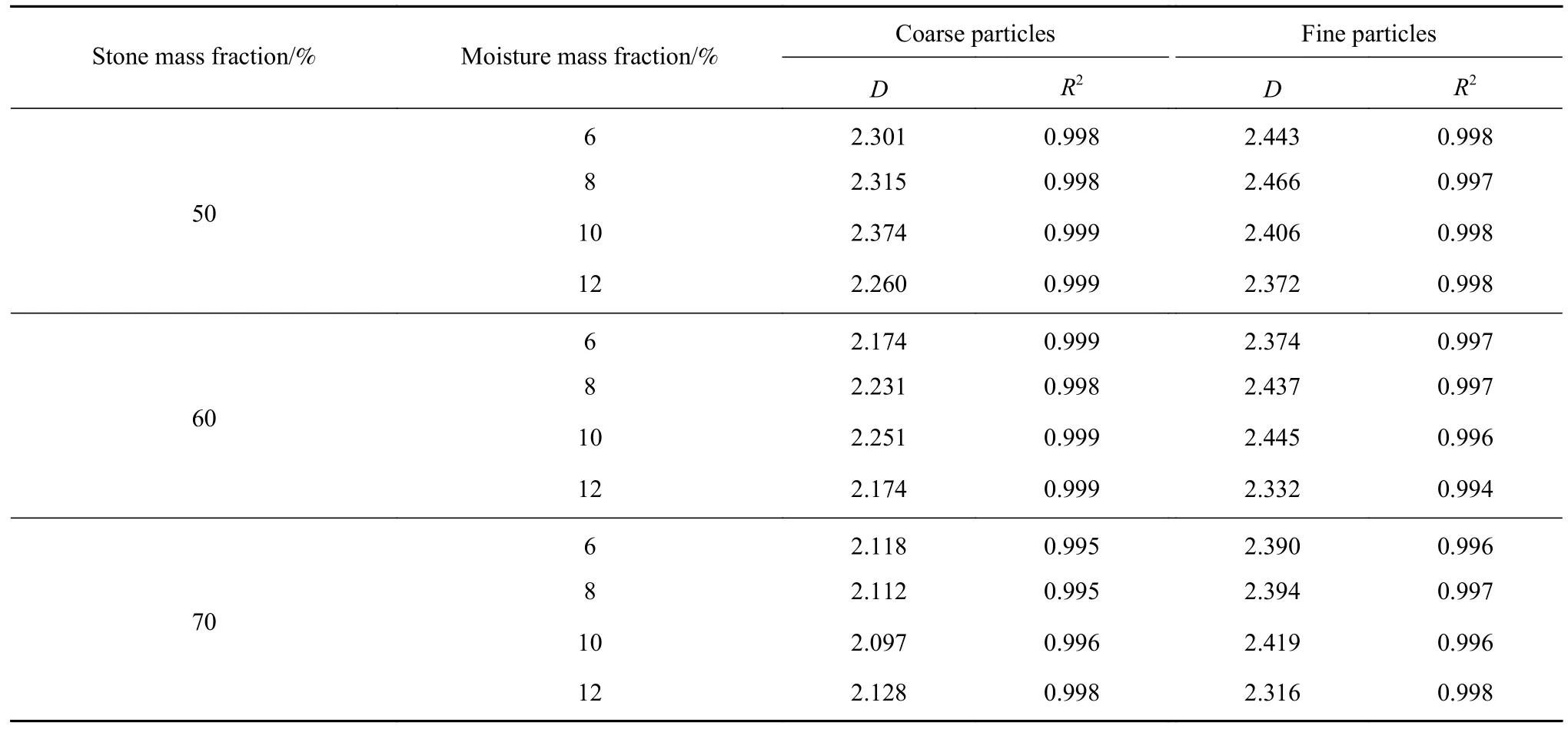
表3 不同配比的分形维数及相关系数Table 3 Fractal dimension and correlation coefficient of different proportions

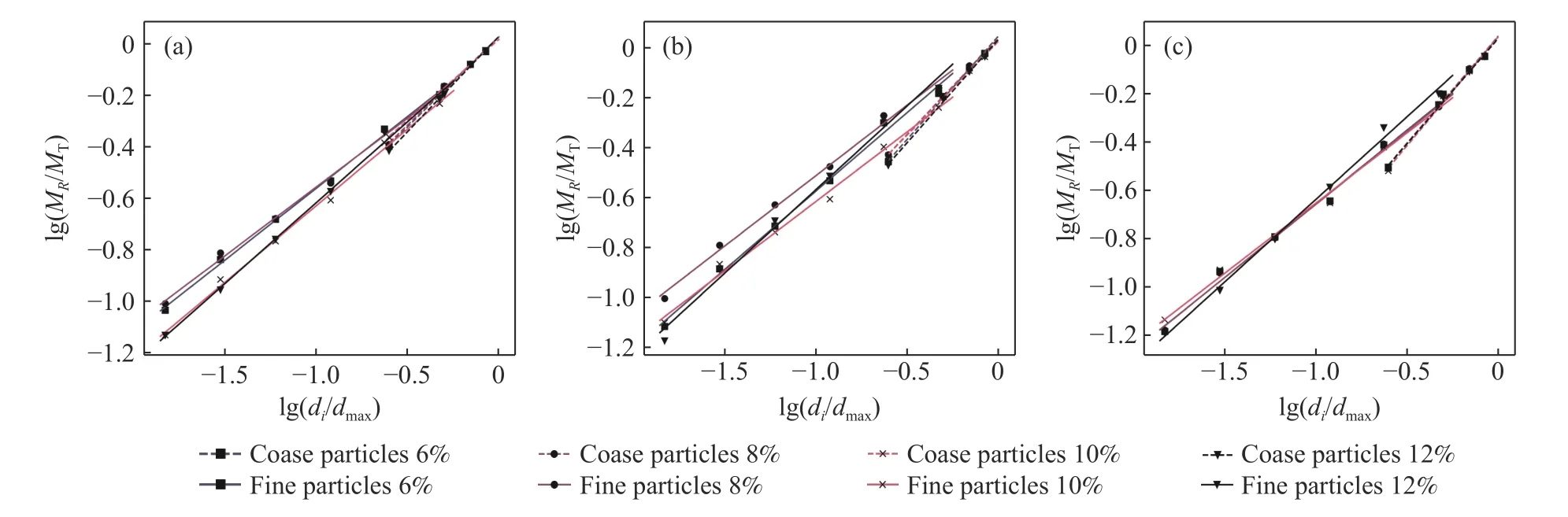
图7 不同配比的分形维数曲线. (a) 含石质量分数50%; (b) 含石质量分数60%; (c) 含石质量分数70%Fig.7 Fractal dimension curves of different proportions: (a) stone mass fraction 50%; (b) stone mass fraction 60%; (c) stone mass fraction 70%

由图7和表3中可以看出，不同配比的分形曲线具有良好的线性关系，相关系数R2均达到了0.99以上，分形模型能够良好的表现碎石土的分型特性. 对D20、D5与含石量、含水率进行非线性拟合分析，结果表明多项式拟合相关性良好，D20和D5的相关系数R2分别为0.952和0.823，得出关系式(6)和(7)：

式中，s表示含石量；w表示含水率.

此外，同一含石量在不同含水率时，粗颗粒的分形维数相近，而细颗粒的分形维数相对差值较大. 结合式(6)和(7)的系数表明粗颗粒含量变化相近，细颗粒含量变化相差较大，即含水率对碎石破裂及破碎的影响较小，对碎石发生研磨的影响更大. 同一含石量中，通常在细颗粒分形维数更大时达到最大干密度，表现出细颗粒的填充对干密度具有积极作用. 含石量对粗颗粒的分形维数影响较大，表明含石量对碎石破裂及破碎有较大的影响，这主要因为含石量会显著影响碎石之间的接触情况，含石率越高，碎石接触的概率越大，进而在冲击荷载的作用下，发生破碎的概率越大. 粗颗粒分形维数的最优区间在2.23～2.25，细颗粒分形维数的最优区间在2.43～2.45，同时分形维数D与破碎率Bg之间也存在图8所示的关联.

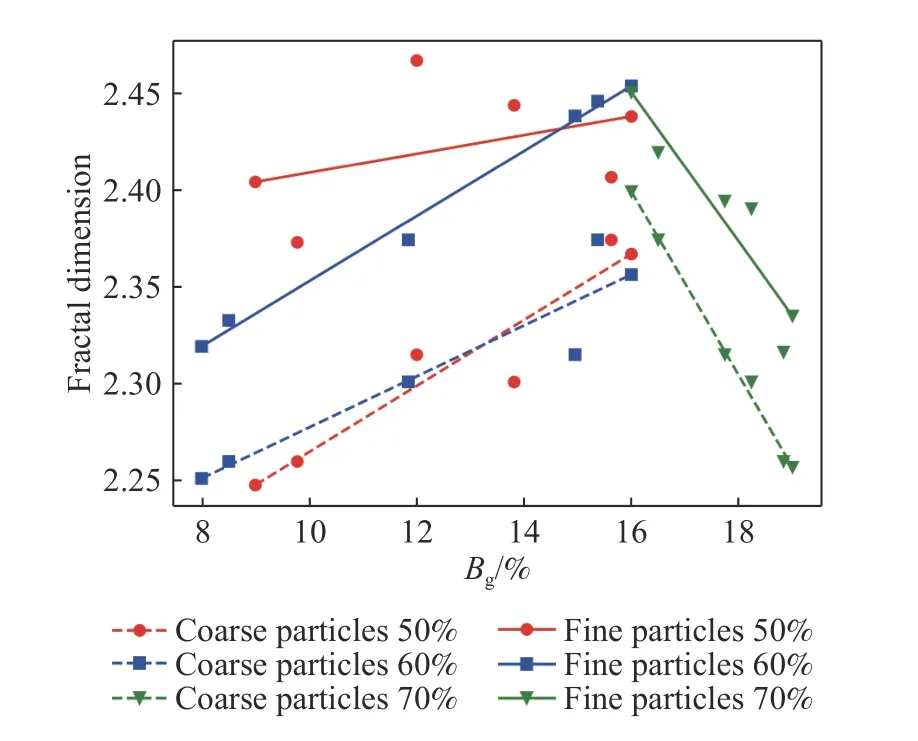
图8 分形维数D与破碎率Bg关系Fig.8 Relationship between D and Bg

从图8可以看出，当含石量不超过60%时，粗、细颗粒的分形维数均随着破碎率的增大而增大；当含石量为70%时，分形维数与破碎率的关系发生较大变化，此时的破碎规律与含石量不超过60%的规律不同，粗、细颗粒分形维数均随破碎率的增大而减小.

3.3 渗透侵蚀特征

由于击实过程导致粒径在1.18～4.75 mm范围内颗粒含量变化具有波动性，而击实对粗颗粒研磨产生的细颗粒含量变化较稳定，因此本文仅讨论了渗透前后粒径小于1.18 mm的颗粒含量变化情况，图9显示了含石量为50%～70%时的不同颗粒含量变化，图中正值表示含量增加，负值表示含量减少.

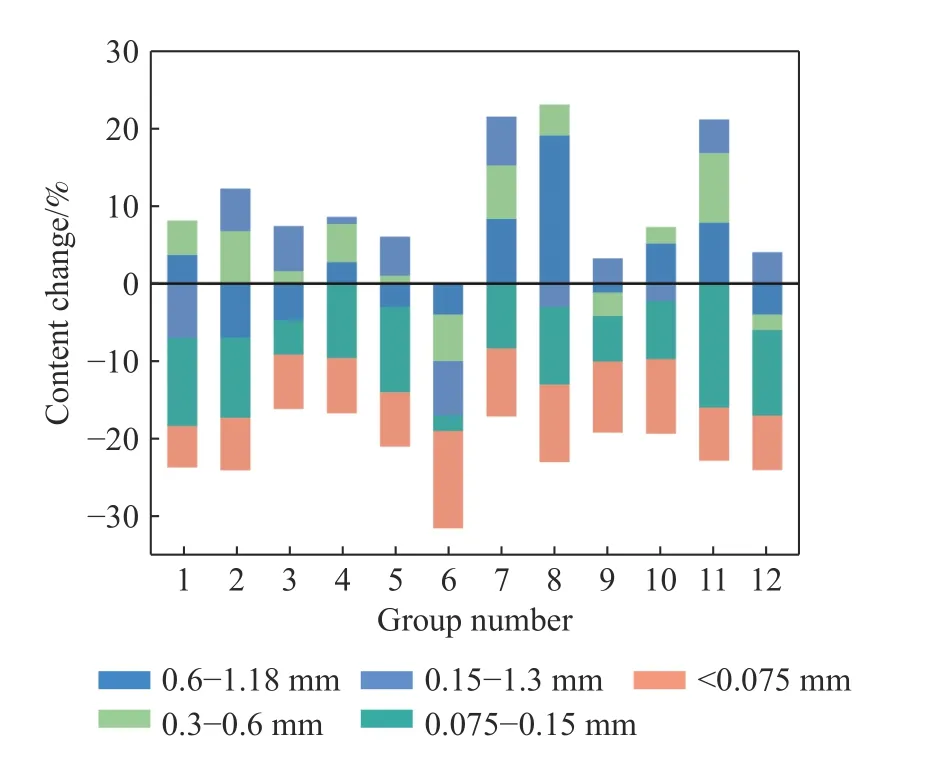
图9 渗透前后颗粒含量变化Fig.9 Change of particle content before and after infiltration

从图9可以看出，正值主要由击实破碎的波动性产生，但仍可以看出粒径小于0.15 mm的细颗粒会发生明显流失，粒径在0.15～1.18 mm范围内的细颗粒会因击实产生含量波动，但也呈现流失趋势. 虽然颗粒含量变化因击实破碎和渗透侵蚀具有一定的波动性，但整体呈现出含石量越高，颗粒流失含量越大的趋势，当含石量超过60%后粒径小于0.075 mm的细颗粒大量流失，流失率约为15%～40%.

分形维数可以反映散体颗粒级配的变化，采用分形维数分析渗透侵蚀对级配变化情况特性.经计算，不同含石量试样渗透前后分形维数如表4所示.

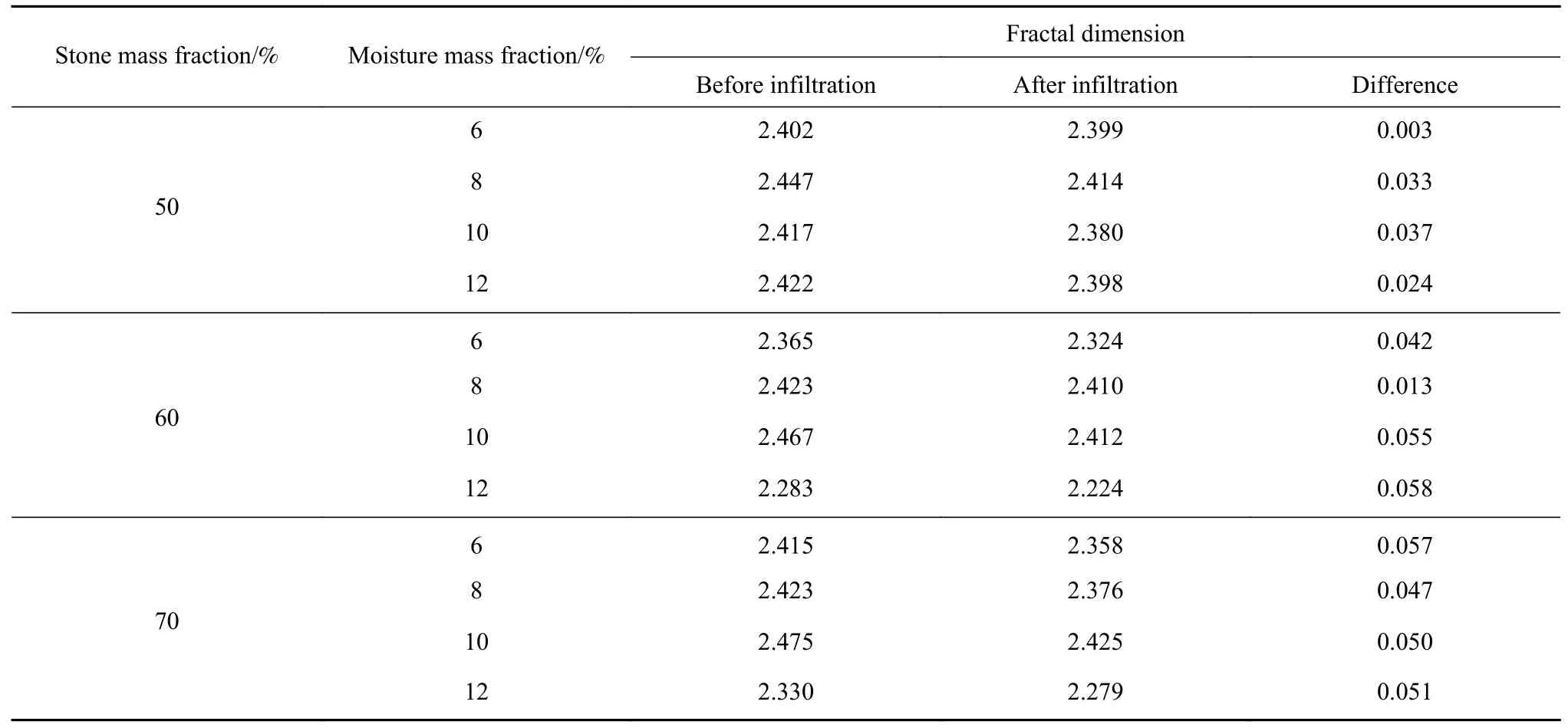
表4 渗透前后分形维数Table 4 Fractal dimension before and after infiltration

从表4可以看出，渗透后细颗粒的分形维数小于渗透前，对于50%含石量的试样，分形维数差值较小且具有一定的波动性，这主要因其细颗粒含量较高，渗透侵蚀影响的含量变化量相对于细颗粒含量不明显. 对于60%含石量的试样，随含水率的不同，干密度越大，渗透系数越小，其渗透前后分形维数的差值越小；70%含石量的试样表现为不同含水率之间分形维数的差值相差不大，这主要由于含石量达到70%时，不同含水率下的渗透系数均较高，此时含水率的变化对细颗粒的侵蚀作用差异影响不明显.