装配式建筑预制混凝土构件的布局优化
2024-04-11王淑嫱阮浩邹贻权刘苗苗
王淑嫱 ,阮浩 ,邹贻权 ,刘苗苗
(1.湖北工业大学 土木建筑与环境学院,武汉 430000;2.北京构力科技有限公司,北京 100020)
“十四五”期间,装配式建筑进入全面发展期,作为推进装配式建筑发展的重要主体,预制混凝土构件生产企业在整个装配式建筑产业链中所处的地位非常关键[1]。然而,当前大部分生产企业存在生产效率低下、管理过程混乱、智能化水平过低等问题,导致企业微利甚至亏损经营。为节约生产成本,企业必须改变当前生产方式,由粗放式生产向精益生产转变,其中预制构件生产布局优化是第一步。目前构件生产布局主要依靠经验,具有随意性和不科学性,为提高模台利用率并减少资源投入,研究预制构件生产定序和定位问题十分必要。
目前,关于布局优化的研究主要集中在原材料切割领域,涉及原材料切割定序和定位问题[2-8]。常用的定位算法包括:最左最下算法(BL)、下台阶算法和最低水平线算法[9-11],其中,BL 算法常导致排样左侧较高,无法充分利用空间;下台阶算法和最低水平线算法排样结果相近,但在某些情况下,下台阶算法会导致排样右侧偏高[12]。最低水平线算法通过确定最低水平线段,使所布物体尽可能放置在该线段最左最下侧,直至最低水平线段放置不下,再重新选择线段并重复操作,直至布局完成。刘少云[13]采用遗传算法与最低水平线算法排样,并将该算法应用于某激光装备企业的板材切割;姚刚等[14]在模型信息的基础上应用最低水平线算法排布构件,从而提高了混凝土预制(Precast Concrete,PC)构件生产的信息化程度和生产效率。
已有的定序智能算法有遗传算法、模拟退火算法和蚁群算法。张娜等[15]采用蚁群算法配合动态最低水平线法,分别计算矩形的排样序列和排放位置。凌晗等[16]使用改进遗传算法进行矩形件排样优化。夏以冲等[17]采用一种自适应遗传模拟退火算法,应用于矩形件优化排样问题。其中遗传算法全局搜索能力较好,但收敛速度慢,易受参数影响;蚁群算法收敛速度慢且易陷入局部优解的情况。灰狼算法是一种模拟狼群狩猎的元启发算法,算法中狼群被分为3 只头狼α、β、γ和普通狼群η,η会根据α、β、γ的位置进行移动并更新自己的位置,每一次更新后也会根据适应值重新选出α、β、γ,直至满足终止条件后得出最优解。徐逸凡等[18]通过灰狼算法解决带AGV 的柔性作业车间调度最小化完工时间问题;麻鹰等[19]使用灰狼算法对18 个影响民航维修人为差错的因子构建了评价模型。相较于遗传算法、蚁群算法等传统智能算法,灰狼算法具有更强的全局搜索能力,收敛速度快,更具有适用性。上述研究仅考虑原料使用率最大,而在预制构件生产中,应综合考虑模台、构件类型和尺寸构成、模具数量、操作空间等复杂条件和约束。
以满足订单生产为目标,采用灰狼算法确定构件顺序,选取最低水平线排布算法确定构件在模台上的位置,充分考虑模台、构件、模具、操作空间等约束,通过不断优化确定构件布置最优方案,使模台的空间利用率最大化,减少模台数量,进一步达到减少人工投入、降低生产成本的目的。
1 预制混凝土构件布局问题分析
现阶段,预制混凝土构件生产方式有流水线式和固定式。流水线式生产是构件与模台一起,按一定顺序,根据不同工序在各工位顺序流转,主要生产叠合板、内外墙体等常规构件;固定式生产是在一个固定模台上完成预制构件所有工序的操作,主要生产楼梯梯段等异型构件,一些小型的作坊式生产企业仅有固定模台生产线,生产所有预制混凝土构件,生产效率低下。流水线式生产方式更符合工业化生产特征,是未来构件厂生产的主流模式。笔者基于流水式生产方式,对构件布局中存在的实际约束进行分析,为建立构件布局优化数学模型提供基础。在此问题中,存在的实际约束包括以下几个方面:
1)模台空间限制。模台为混凝土或钢制矩形操作平台,预制构件生产过程是以模台为载体布置模具和构件,根据工序模台在不同工位顺序流转,常见尺寸为:宽3.5~4 m、长9~12 m,在生产过程中,任何模具和构件(含出筋长度)均不能超出模台范围。
2)构件布局尺寸计算。与一般矩形原材料不同,预制混凝土构件有叠合板、梁、柱、墙体等多种类型,很多构件有外伸钢筋,构件在布局中的尺寸应为模具尺寸和构件外伸钢筋长度总和。
3)构件摆放要求。为便于操作和质量控制,构件的各边应平行或垂直于生产模台的长和宽,构件不能重叠摆放,构件之间应预留操作空间。
4)模具数量限制。构件生产过程中,模具为周转材料,由于成本较高、模具数量有限,每次可同时生产的某类型构件数量不应大于其模具数量。
在以上约束限制下,优化过程可以分为两部分。
1)确定布局的顺序
预制构件厂主流的生产模式为按订单组合(Assemble-to-Order,简称为ATO)生产模式,即生产方在收到来自不同施工方的订单后,根据各类订单吊装需求对订单进行重新组合,生成工厂生产计划,同一生产批次有不同类型、不同尺寸的多个构件,然后确定构件的生产顺序。采用灰狼算法作为定序算法,灰狼算法是根据灰狼群体的捕猎行动而提出的优化算法,具有较强的局部搜索能力和全局搜索能力。主要步骤为:①初始化灰狼种群,确定狼群的初始位置;②计算各灰狼适应度,保留排名前3 位的头狼;③更新灰狼位置;④计算适应度,并重新确定3 只头狼;⑤重复③、④,直至达到最大迭代次数。
2)确定布局的位置
构件布局顺序确定后,通过最低水平线算法确定构件在模台上的位置。最低水平线算法的优点在于排布时更加平均,不易存在排件扎堆的情况,对于空间的利用效率更高。最低水平线算法的主要步骤为:①找到当前的最低水平线段;②在约束条件限制下,将构件置于最低水平线段上,尽可能向最左侧移动;③若最低水平线段放置不下,则转入次低级水平线段进行排布;④若所有最低线段均排布不下,则转入下一块模台。
构件生产布局问题可视为二维排布问题,即在有限的布局空间内,考虑实际约束,通过确定构件生产顺序和布局方法,使模台空间利用率最大化。
2 建立预制混凝土构件排布数学模型
根据预制构件厂实际生产条件和流水线式生产方式,模型可以描述为:以工厂生产计划为排布对象,以实际约束为前提,应用最低水平线法确定构件位置,通过不断优化得到的最优布局方案中所占模台总长度LZ最短(所占模台数量最少)。
模型的约束条件:
1)总布局构件数量符合订单所需数量要求;
2)布置构件时,构件不能超过模台所占范围;
3)所有构件之间不能相互重叠;
4)布局某类构件时,其布置数量不能超过该类构件的模具数量;
5)模具的各边与模台边平行,不存在倾斜布置的情况;
6)考虑外伸钢筋长度和构件间的操作空间。
上述约束的数学表达和基于最低水平线法的数学模型的建立过程如下:
1)确定模台坐标系和构件位置表示方法
设模台的长为L,宽为W,该模台左下角点为原点(0,0),以模台长边为x轴,模台宽边为y轴建立直角坐标系,xi,yi为坐标系内的横纵坐标。其中,xi≤L,yi≤W,xi,yi≥0。
任意一个预制构件的位置可描述为
式中:xi0,yi0为该构件左下角位置点的坐标值;xi1,yi1为右上角位置点的坐标值。
按照最低水平线法的布局规则,找到最低水平线段并尽可能向其最左侧布置,可以得出xi0,yi0,xi1,yi1的坐标计算公式。
式中:xleft为在最低水平线段上构件所能放置的最左侧点的横坐标值;ylow为最低水平线段的纵坐标值;l为平行于模台长边的构件长度;w为平行于模台宽边的构件长度。
2)考虑出筋长度和操作空间
为保证构件有适当的钢筋伸长量占用空间和操作空间,对构件尺寸做出规定
式中:lpc为该构件本身平行于模台长边的长度;wpc为该构件本身平行于模台宽边的长度;lg为外伸钢筋长度;lc为预留操作空间长度(其中预留操作空间长度表示某构件与其左右相邻两个构件之间需要保留的长度和)。
3)确定布局方式和约束条件
为满足构件不相互重叠的要求,布置方式和约束条件如图1 所示。
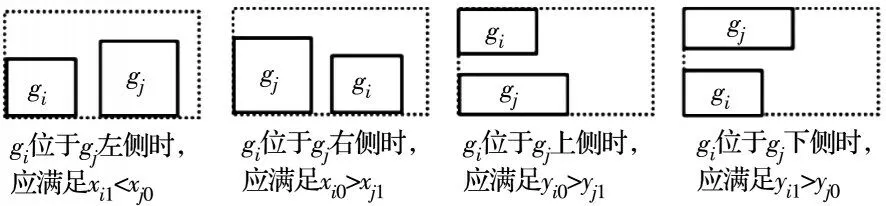
图1 构件分布情况Fig.1 Component distribution
4)计算构件和模具约束关系
设布局情况为
式中:Bi为第i次的布局情况;gin为第i次布局的第n个构件。
每次布局,构件数量不能超过模具数量,因此,构件所属种类模具数Sm应大于等于该类构件在本次布局中的数量值Sg,即Sm≥Sg。
5)目标函数的表达
最终优化目标为布局长度最短,其目标函数为
式中:LBi为第i次布局时的横向长度;Ni为第i次布局时占用模台的数量;LLi为第i次布局时,最后一块模台所占用的横向长度。
式中:LZ为本生产批次所需布局总长度之和。
6)预制混凝土构件布局数学模型
构建函数
在满足式(11)约束条件的情况下,通过重复计算构件坐标值(式(12)),最终得到目标函数解值(式(13))。
3 基于灰狼算法和最低水平法的布局优化算法
布局优化算法的核心思想是:通过灰狼算法不断优化待排预制构件的排入顺序,再由最低水平线算法将排入序列转化成模台布局方案。整体优化过程是由多约束条件限制的寻找最优解的复杂数学问题,核心算法设计如下:
设某生产方案为
其中变量xi为生产计划中的一个构件。
令每个生产构件xi为
式中:T为构件的类型;Ls为构件的短边长度;Ll为构件的长边长度。
按规定条件和约束条件得到其一组分布情况为
式中:bij为第i次布局时的第j个构件。
定义差异数组
另外,在迭代优化过程中,为使算法不陷入局部最优解的情况,设置灰狼的自由系数f,其取值范围在[0,10]之间,数值越大,全局搜索能力越强,但收敛速度越慢,除3 只头狼外,位移时其他狼群自由移动的概率为
算法的主要流程如图2 所示,其详细步骤如下:

图2 基于灰狼算法和最低水平线排布算法的布局优化流程图Fig.2 Layout optimization flow chart based on grey wolf algorithm and minimum horizontal line algorithm
步骤1:输入初始种群数、最大迭代次数、模台和模具的基本信息、生产计划的基本信息。
步骤2:建立约束条件,通过式(11)的设置,实现构件摆放、模具数量限制等要求。
步骤3:由步骤1 键入的基本信息和步骤2 中的约束条件,随机生成初始灰狼种群并进行编码处理,最终得到一组随机的构件初排序列。
步骤4:使整个灰狼种群按照最低水平线法进行布局,计算整个灰狼种群的适应度,并选择排名最靠前的3 只灰狼α、β、γ作为整个灰狼种群的头狼,将其他狼定义为狼群η。
步骤5:狼群η需要按照3 只头狼α、β、γ的位置调整自己所处的位置,η中每一只灰狼都会在α、β、γ这3 只领头狼中随机选取一只作为参照,根据差异数组判别可调节部位,并根据追随系数ε、自由系数f对每个部位做出相应调整。
步骤6:重复步骤4、步骤5,直至达到最大迭代次数,得到最优解。
4 案例分析
4.1 项目概况
以武汉市某PC 构件生产基地的一批叠合板生产任务为例,该批次叠合板需求量为87 块,共有21种尺寸类型,采用流水式生产,其构件数量、模具数量和尺寸等详细信息如表1 所示。工厂配备的模台尺寸为4 m×10 m,叠合板为双向出筋且出筋长度均按0.15 m 计算,预设工人操作空间为0.6 m。

表1 生产需求及构件信息Table 1 Production requirements and component information
4.2 数据预处理
批次划分是根据模具的数量和需要生产的构件数量并本着最大化利用模具资源的原则来确定的。假设某类构件的需求量为5 个,该类构件模具数为3。由于一批最多生产3 个,则该构件应分2 个批次进行布局操作,每个批次布局数量分别为3、2。数据的预处理使案例的布局符合实际约束限制,保证优化结果真实有效。因此由表1 分析,需要将本项目分两次进行生产,第1 次生产45 个构件,第2 次生产42 个构件,构件待排信息如表2 所示。

表2 待排构件信息Table 2 Component information to be arranged
4.3 传统排布方式模拟
在实际生产过程中,工厂生产管理人员依据个人经验随机安排构件生产顺序和模台布置,在本案例中,应用Python 的随机处理功能,通过随机生成500 组布局情况并求出其平均值作为传统生产布局的参照值。通过计算,87 块叠合板分两次生产,共占模台总长度为358.23 m,占用模台数37 个。
4.4 基于灰狼算法的优化实现
应用Python 编译工具PyCharm Community Edition,通过编码实现构件定序和定位优化算法。通过不同参数对比试验,选取收敛效果好、资源消耗低的一组参数。因此,基于最低水平线的灰狼算法相关参数设置如下:种群数为500,最大迭代次数为100,追随系数为4,自由系数为2,运行代码得出迭代过程,如图3 所示。第1 次生产45 个构件,通过不断优化,目标函数构件所需模台总长度由162.97 m降为147.84 m,迭代次数为74 次后趋于平稳;第2次生产42 个构件,通过不断优化,目标函数构件所占模台总长度由149.50 m 降为139.96 m,迭代次数为33 次后趋于平稳。两次生产排布迭代过程变化趋势如表3、表4 所示。最优构件布局方案中,87块叠合板分两次生产,共占模台总长度为287.80 m,占用模台数29 个。最终迭代后的构件布局情况如图4、5 所示。

表3 第1 次生产布局顺序优化主要迭代过程Table 3 Main iterative processes for first production layout sequence optimization

表4 第2 次生产布局顺序优化主要迭代过程Table 4 The main iterative process of second layout production sequence optimization
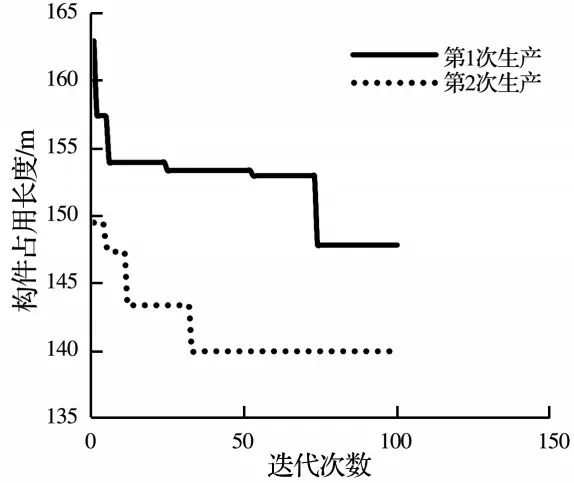
图3 构件排布优化迭代过程Fig.3 Iterative process of component layout optimization
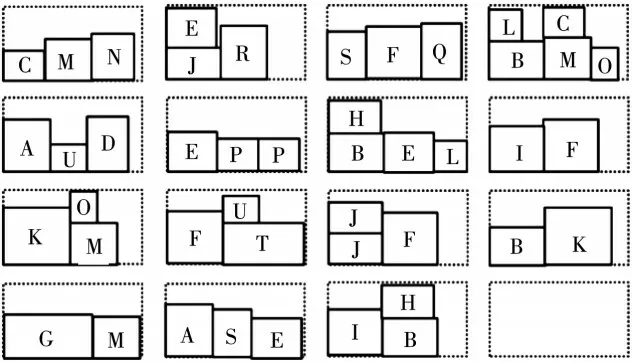
图4 第1 次生产45 个构件最优布局图Fig.4 Optimal layout for the first production of 45 components
4.5 基于灰狼算法的优化结果分析
由图3 可知,基于最低水平线的灰狼算法能够有效地朝着最优解不断优化,在迭代后期,目标函数值基本保持稳定。表3 和表4 能反映出各个构件在不同排序下对目标函数的影响及最优排序方案,图4 和图5 能直观展示出每张模台上预制构件的布置方案。按传统人工排布方式,87 个叠合板共占用模台数37 个,优化后占用模台数为29 个,模台利用率提高了21.6%。另外,模台占用数量减少后,所需操作工人的数量也相应减少,可进一步节约生产成本。

图5 第2 次生产42 个构件最优布局图Fig.5 Optimal layout for the second production of 42 components
由计算过程和优化结果可知,基于最低水平线的灰狼算法能够在较短时间内得到一个明显优于传统情况的构件排序和定位方案,适用于预制混凝土构件排件布局优化。由Python 语言完成算法设计后,生产管理人员可以便捷地通过Excel 表格导入生产构件信息,可大大降低对个人经验的依赖程度,实现科学排序和定位。优化后的模台布置图一目了然地展示了布局方案,便于车间组织生产。
4.6 灰狼算法与其他智能优化算法的对比分析
为了更直观地体现灰狼算法在构件布局优化问题上的高效性和优越性,采用模拟退火算法(SA)和遗传算法(SA)对案例进行优化,并对其优化结果进行分析。其中,模拟退火算法参数设置情况为:初始温度1 500 ℃,温度下降速度0.98,迭代次数1 000 次;遗传算法参数设置情况为:种群数500,迭代次数100,交叉概率0.7,变异概率0.05。
表5 和表6 列出了3 种算法的运行结果对比情况,表7 列出了3 种算法的性能指标对比情况。

表5 第1 次生产优化结果对比Table 5 Comparison of the first production optimization results

表6 第2 次生产优化结果对比Table 6 Comparison of the second production optimization results
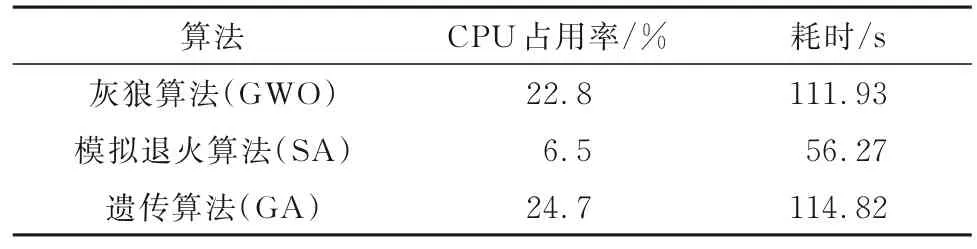
表7 算法性能指标对比Table 7 Comparison of algorithm performance indexes
由表5、表6 可知,与SA 和GA 相比,第1 次生产时灰狼算法的优化结果分别缩短了21.55、9.9 m,差距分别为12.72%和6.28%;而第2 次生产时灰狼算法同样优于SA 和GA,差距达到16.16% 和7.89%。综合表7 分析,模拟退火算法运行时资源占用和耗时很少,但优化效果一般;遗传算法资源占用和耗时多,优化结果较好;灰狼算法资源占用和耗时多,略微低于遗传算法,但优化效果更好,表明在布局问题的应用上灰狼算法更加理想和高效。
5 结论
与已有研究相比,建立的最低水平线数学模型更符合构件厂实际生产情况,更具适用性。在构件排布定序算法中,应用灰狼算法不断优化待排预制构件的排入顺序,再由最低水平线法将排入序列转化成模台布置图,形成最优布局方案。将灰狼算法结果与遗传算法和模拟退火算法进行综合对比发现,灰狼算法的优化效果最好。该优化方法能提高模台空间利用率,提高模具利用效率,进一步节约生产成本,且在构件生产规模越大时优化效果越显著。通过Excel 表格将构件信息导入模型和算法中运行,即可快速计算出优化后的布局方案,具有较好的实用性。最后,通过案例分析,验证了算法可以在较短时间内得出布局结果,并使模台利用率提高21.6%。在未来的研究中,将以此成果为基础,进一步研究流水线式生产模式下构件整体调度优化问题。
