双目标优化与生成对抗网络结合的框架结构阻尼器布置方案智能设计方法

潘毅 ,陈齐 ,王腾 ,周祎

（西南交通大学 a.土木工程学院；b.抗震工程技术四川省重点实验室，成都 610031）

目前，结构减震设计大多采用被动控制技术[1]，且多采用耗能减震设计，即在结构的合理位置布置适宜数量的阻尼器来消耗地震能量，减小结构地震反应。适宜的阻尼器数量、位置是减震设计的关键。减震设计流程大致可分为阻尼器竖向布置和阻尼器平面布置。在阻尼器竖向布置方面，将阻尼器布置在合理楼层位置，能增强耗能效果、提高抗震能力[2]。为实现减震性能和经济性的平衡，应将尽量少的阻尼器布置在最优的楼层位置，以最大限度发挥阻尼器的耗能减震性能并降低经济成本。但目前的减震设计布置方法既不能保证阻尼器布置是最优方案，又要进行繁琐的迭代，其效率有待提高[3]。在阻尼器竖向布置方面，高效、合理地确定各楼层阻尼器数量是结构减震设计亟须解决的问题。在阻尼器平面布置方面，基于阻尼器竖向布置得到各楼层阻尼器的合理数量之后，需要为各楼层阻尼器选择合理的安装位置，确定阻尼器平面位置是一个迭代、调整和耗时耗力的过程。因此，在满足业主使用功能与阻尼器平面布置规则的前提下，快速确定阻尼器平面安装位置是结构减震设计亟须解决的问题。为解决上述问题，众多学者进行了阻尼器竖向布置优化方法和阻尼器平面布置优化方法的探索与研究。

在阻尼器竖向布置优化方面，因阻尼器布置与结构地震响应之间无明显、有规律的显式关系，故目前的阻尼器竖向优化布置大多采用随机搜索优化布置方法和遗传算法。例如，Agrawal 等[4]采用3种智能搜索算法，即序列、WOBI 和ESPS，研究在不同类型目标函数下的阻尼器最优位置，结果表明，通过最小化的结构最大层间位移目标函数得到的阻尼器最佳位置取决于具体地震动，WOBI 和ESPS 在改善序列搜索最佳位置方面有效。李钢等[5]基于遗传算法，提出一种应用于耗能减震结构参数设计的新型优化数学模型，结果表明，新模型是一种有效的优化设计方法。李宏男等[6]基于遗传算法，提出阻尼器新型优化数学模型，对比了位移型和速度型阻尼器优化布设的差异，发现高层建筑宜选用速度型阻尼器。燕乐纬等[7]基于数字序列编码遗传算法，提出高层结构黏滞阻尼器优化布置方法，结果表明，该算法能加速种群进化，在高层结构阻尼器优化布置上有效。马宏伟等[8]基于粗粒度并行遗传算法，提出通过Matlab-ABAQUS-Python 的交互使用来优化被动控制结构中阻尼器位置的方法，结果表明，该算法能显著提高结构减震率。金波等[9]基于改进的遗传算法，提出以替换杆件模态应变能百分比之和最大为适应度函数来优化大跨网架结构上的黏滞阻尼器数量和位置的方法，结果表明，该方法能明显改善结构受力状况，减震效果良好。王曙光等[10]采用遗传算法进行多种不同类型阻尼器的同步优化布置，结果表明，该算法可以在较短时间内同时优化不同类型的阻尼器位置。陈丰收等[11]采用多目标并行遗传算法进行减震结构的阻尼器布置数量和布置位置的多目标同步优化，结果表明，该算法收敛性强，阻尼器主要布置在结构中下部且中部较多。周玉娴等[12]采用基因属性保留遗传算法进行阻尼器的双目标同步优化布置，结果表明，该方法可高效处理双目标阻尼器同步优化问题。尽管以上研究在阻尼器竖向优化布置方面已经很成熟，但是较少同时考虑阻尼器的竖向布置与平面布置，即在确定各楼层的阻尼器数量后，需要考虑在不妨碍业主使用功能需求且不增大刚度与质心差异、结构扭转效应的前提下，在各楼层平面上合理布置阻尼器。

在阻尼器平面优化布置方面，目前处于起步阶段，相关研究较少。例如，Erdem Çerçevik 等[13]采用蝙蝠算法和蜻蜓算法进行黏性墙式阻尼器数量、阻尼器周边布置的优化，并以楼层加速度和层间位移角为约束条件，结果表明，该方法有利于改进结构响应、最小化经济成本。程卫红等[14]通过模型算例针对墙式连接位移型阻尼器进行了平面布置分析，结果表明，阻尼器平面布置宜规则对称，且尽量布置在框架结构周边，从而减少不规则布置带来的附加扭转效应。目前针对阻尼器智能选择平面位置方面的研究较少，为实现和加速减震设计的智能化，有必要开展相关研究。

针对以上不足，笔者基于双目标优化算法（Dual Objective Optimization Algorithm，DOOA）和生成对抗网络（Generative Adversarial Network，GAN），提出阻尼器竖向优化布置与智能选择阻尼器平面位置的方法。采用双目标优化算法进行阻尼器竖向布置，并与原结构、工程师设计、逐层逼近法进行对比分析；采用生成对抗网络进行阻尼器平面布置，并与工程师设计结果进行相似性差异度对比分析。通过工程案例的应用与分析，验证方法的有效性，为减震结构的智能化设计提供参考。

1 阻尼器竖向布置优化目标

1.1 减震结构运动方程

在地震作用下，未设置阻尼器的框架结构的运动方程为

式中：M、C0、K0分别为未布置阻尼器的框架结构的质量矩阵、阻尼矩阵和刚度矩阵；(t)(t)、u(t)分别为框架结构的楼层加速度向量、速度向量和位移向量；P(t)为阻尼器所提供的阻尼力矩阵；(t)为地面加速度，即地震动加速度；I为单位列向量。

为兼容多种速度型阻尼器的力学模型，考虑3种常见的速度型阻尼器力学模型，包括线性模型、Kelvin 模型和Maxwell 模型，3 种模型均假设阻尼指数为1。线性模型的阻尼力表达式为

式中：Cd为阻尼器的阻尼矩阵；(t)为第i层楼面相对基础的变形速度。将式（2）代入式（1），可得到布置线性阻尼器模型的框架结构运动方程。

由式（3）可得出，线性阻尼器模型只改变了结构的阻尼矩阵。

Kelvin 模型采用的是刚度与阻尼并联的形式，如图1 所示。在实际减震设计中，一般设置刚度Kd=0，以此来让阻尼装置在地震作用下运动起来，故Kelvin 模型的阻尼力矩阵表达式为

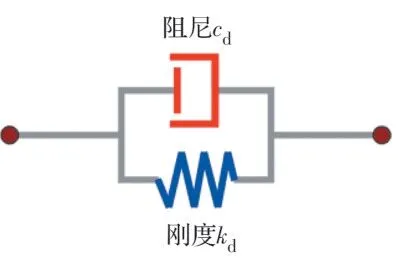
图1 Kelvin 模型Fig.1 Kelvin model

式中：Kd为阻尼器的刚度矩阵；Cd为框架结构的层间侧移刚度矩阵；u(t)为楼面相对基础的变形向量。将式（4）代入式（1），可得到布置Maxwell 阻尼器模型的框架结构运动方程同式（3）。

Maxwell 模型采用的是刚度与阻尼串联的形式，如图2 所示。在实际减震设计中，一般设置刚度为阻尼系数的100～1 000 倍，从而让阻尼装置消耗地震能量，故项可忽略不计，Maxwell 模型的单个阻尼器阻尼力表达式为

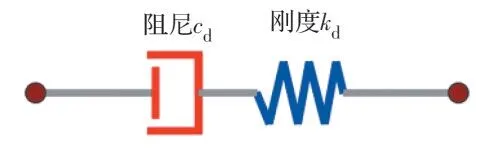
图2 Maxwell 模型Fig.2 Maxwell model

式中：p(t)为单个阻尼器提供的阻尼力(t)为单个阻尼器两端相对变形速度大小。将式（5）代入式（1），可得到布置Maxwell 阻尼器模型的框架结构运动方程同式（3）。

综上所述，当阻尼指数为1 时，3 种阻尼器模型的结构运动方程在形式上统一，均为式（6）形式。

1.2 减震结构响应求解

在布置阻尼器后，框架结构的阻尼体系变为非经典阻尼体系，即非对角矩阵，运动方程组无法解耦为N个独立的单自由度体系运动方程。为解决此类非经典阻尼解耦问题，采用复振型分解法进行方程组解耦，由线性定常动力体系的微分方程经变量代换得到减震结构体系的状态方程[15]。具体表达式为

因矩阵D为非对称矩阵，故应采用广义模态分析法进行解耦，通过特征向量的正交性计算框架结构的地震响应。假设非对称矩阵D的左、右特征向量与特征值分别为θi、φi、λi，其中i=1,2…2N。

由于振型的正交特性，框架结构的任何响应均可采用振型的线性组合进行表示。例如，采用右特征向量进行振型的线性组合，如式（8）所示。

式中：φ=[φ1,φ2…φi…φ2N]，η(t)为单模态坐标向量。

将式（8）代入式（7）可得

式（9）两侧同时左乘进行解耦

在确定的地震激励作用下，减震结构单模态响应为

因此，框架结构的楼层位移响应向量可表示为

框架结构的楼层加速度响应向量可表示为

1.3 竖向布置优化目标函数

在布置阻尼器后，一般需减小框架结构的楼层加速度峰值与层间位移角峰值，故采用多目标优化方法，优化目标函数为

2 阻尼器平面布置评价指标

2.1 布置规则

基于框架结构的平面建筑图，进行阻尼器的平面布置。在已确定框架结构阻尼器竖向布置的基础上，对需要布置阻尼器的楼层进行智能化平面布置。依据《全国民用建筑工程设计技术措施——结构（结构体系）》规范附录C.4，阻尼器平面布置应符合表1 所示的规则。

表1 平面布置规则Table 1 Rules of plane placement

2.2 评价指标

基于阻尼器平面布置规则，以较优的目标设计为设计标准，提出用于评价生成设计的相似性差异度综合评价指标E，以及两个子指标：阻尼器质心差异度、阻尼器分散性差异度。质心差异度可以反映阻尼器质心与结构质量中心之间的差异程度，该值越小则阻尼器布置越对称，其附加扭转越小。分散性差异度可以反映阻尼器是否分散布置，该值越小则结构抗扭转能力越强。将生成的平面布置与目标设计的平面布置进行逐楼层、逐柱跨对比，通过式（15）～式（17）计算两者的相似性。E值越小，说明生成设计与目标设计之间的差异越小，相似程度越高。当相似性差异度综合评价指标E小于临界值α时，则生成设计与目标设计相似性极高，结构的抗扭能力较好。

式中：E为生成设计的相似性综合评价指标；为生成设计与目标设计在阻尼器质心上的距离大小；为生成设计与目标设计在第j层楼的阻尼器分散程度上的差异大小；n为框架结构楼层数量；xg、yg分别为生成设计第j层楼X向、Y向阻尼器质心与结构质心x0、y0之间的距离；xe、ye分别为目标设计第j层楼X向、Y向阻尼器质心与结构质心x0、y0之间的距离；L、B分别为框架结构的长度与宽度；xgi、xei分别为生成设计、目标设计第j层楼第i个阻尼器与结构质量中心x0之间的距离；ygi、yei分别为生成设计、目标设计第j层楼第i个阻尼器与建筑质量中心y0之间的距离；n1、n2分别为生成设计、目标设计的X向与Y向阻尼器数量之和。

需要说明的是，生成设计是基于提取的可布置阻尼器位置图像进行的图像生成，如图3 所示，即需要对图纸做前处理工作。

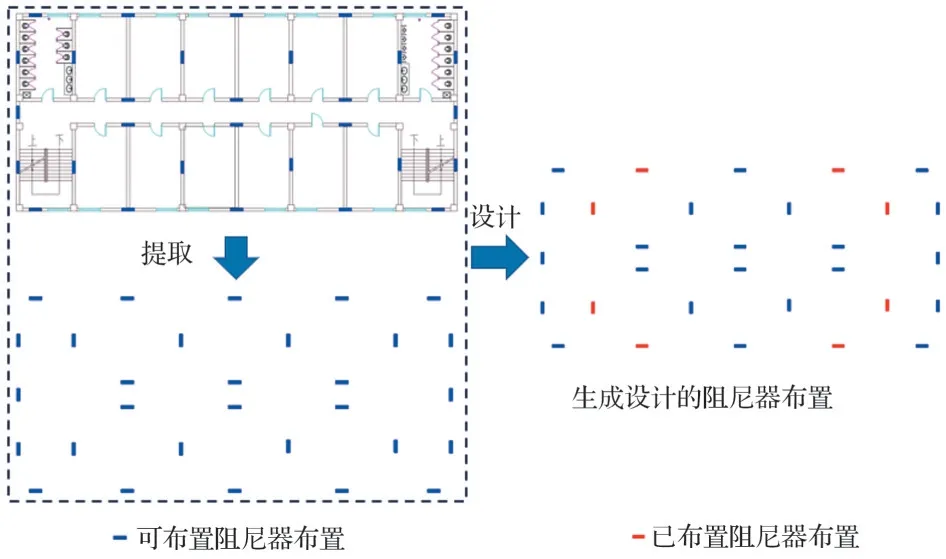
图3 生成设计图像Fig.3 The figure of generate design

3 阻尼器布置智能设计算法

3.1 阻尼器竖向智能布置

采用双目标优化算法来实现阻尼器的竖向布置。双目标优化算法是借鉴了麻雀搜索算法的优化思想,通过模拟麻雀搜索食物的行为来寻优，从而寻找最优解。在一个D维搜索空间内，存在pop只个体，第i只个体在搜索空间中的位置可表示为Xi=[xi1…xij…xiD]，i=1,2…N，其中xij为第i只个体在第j维空间的位置。基于双目标优化算法的阻尼器竖向布置流程图见图4，具体步骤如下。

图4 阻尼器竖向智能布置流程图Fig.4 Flow chart of damper vertical intelligent placement

Step1：初始化数据，种群规模pop，优化目标函数维数D，迭代次数T，初始值上下界lb、ub。

Step2：初始化种群，生成pop 个D维向量Xi，维度对应楼层数量。

Step3：计算个体的目标函数值f1和f2，选出优化目标函数f1和f2均相对较小时所对应的个体作为最优解。

Step4：循环执行step2、step3，迭代T次，每次迭代后更新阻尼器竖向布置最优解。

Step5：当迭代次数t=T，程序结束，输出最后一次迭代所得到的阻尼器竖向布置最优解。

3.2 阻尼器平面智能布置

采用GAN 来实现阻尼器的平面布置。GAN是自动化建筑设计中应用最广泛的框架之一[16]，是一种深度生成模型，该模型框架包含两个相互竞争的神经网络结构：判别器D 和生成器G。生成器用来捕获数据分布并生成样本，而判别器用于将生成的样本与真实样本区分开来[17]，二者通过对抗学习提升各自的能力。生成对抗网络可通过对既有设计图像或文本的学习，掌握已有设计数据中的潜在设计规律，实现新设计图像的生成[18]。基于GAN 的阻尼器平面布置流程图见图5，算法具体步骤如下。

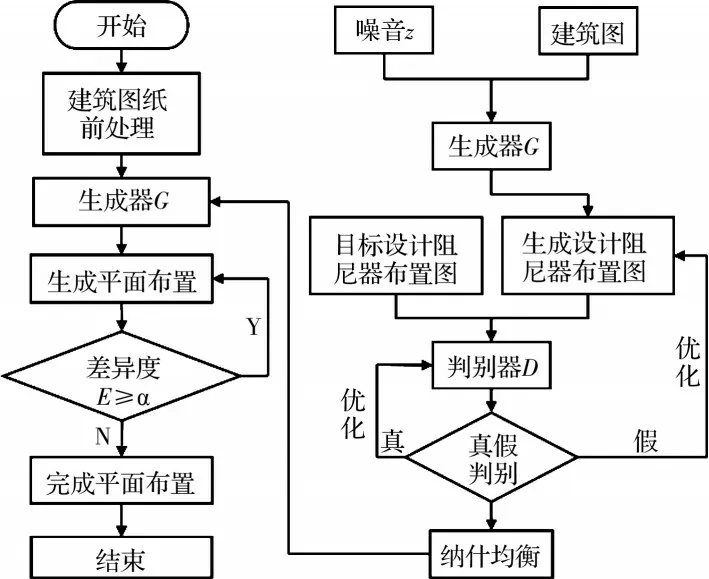
图5 阻尼器平面智能布置流程图Fig.5 Flow chart of damper plane intelligent placement

Step1：将用于训练、验证和测试的建筑平面图进行前处理，即用蓝色标出所有能布置阻尼器的位置，用红色标出已布置阻尼器的位置。

Step2：将建筑平面图纸的所有合理阻尼器布置用于训练生成器，在与判别器博弈过程中，不断学习阻尼器布置规律。当达到纳什平衡时，生成器训练完成，可用于阻尼器平面布置。

Step3：将训练好的生成器用于生成与工程师设计相似的阻尼器平面布置，从而得到平面布置的生成设计。

Step4：采用相似性差异度综合评价E进行生成设计评价。若E≥α，返回到step3 中重新进行训练和生成，重新评价，直至E＜α。

4 阻尼器布置智能设计工程应用

为研究双目标优化算法和生成对抗网络的可行性和通用性，采用2 个实际减震设计工程案例进行阻尼器布置设计，并开展性能分析、对比。基于阻尼器竖向布置双目标优化算法和阻尼器平面布置生成对抗网络算法，对地震动作用下的框架结构进行阻尼器竖向布置与平面布置，在竖向布置上与逐层逼近设计、工程师设计进行对比，在平面布置上与工程师平面设计进行对比，从而验证阻尼器布置方法的有效性。

4.1 工程案例一

4.1.1 结构模型

某5 层钢筋混凝土框架结构教学楼，首层层高4.9 m，标准层层高4 m，总高20.9 m；柱截面为600 mm×600 mm，边主梁截面为500 mm×800 mm，内主梁截面为400 mm×800 mm，次梁均为300 mm×600 mm，具体结构平面布置如图6 所示，各楼层的质量和刚度见表2。抗震设防烈度为8 度（0.2g），地震分组为第2 组，场地类别为Ⅱ类，设防类别为乙类。

表2 某5 层RC 框架结构的质量和刚度Table 2 The mass and stiffness of a five story reinforced concrete frame structure

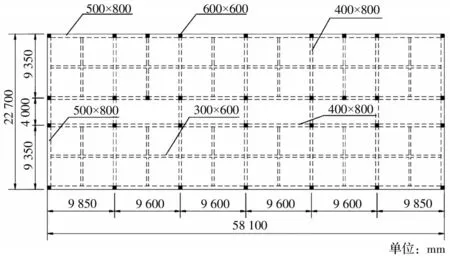
图6 案例一框架结构平面布置Fig.6 Plane placement of frame structure of case one

按照工程师试算，案例一结构需安装30 个黏滞阻尼器，具体阻尼器参数见表3。优化并求解阻尼器合理位置，提高框架结构在地震波作用下的抗震性能，使其层间位移角和楼层加速度满足一定的减震目标，具体减震指标为：在8 度罕遇地震作用下，层间位移角控制在1/200 以下，楼层加速度控制在5 m/s2以下。

表3 阻尼器参数Table 3 Parameters of dampers

4.1.2 阻尼器竖向优化布置

依据场地特征周期Tg1=0.45 s、结构基本周期Ta1=1.25 s，选取与其周期相近的3 条地震动：SAN FERNANDO（台站110）波、COALINGA（台站1624）波、NORTHRIDGE（台站5366）波，分别记为A 波、B波、C 波，并将地震波的峰值加速度调整至400 cm/s2。

在不同地震波作用下，双目标优化算法能保持目标函数值f1、f2变动幅度较小，且在同一方向上的阻尼器布置近似相同，反映了该算法对不同地震动的鲁棒性能较好。同一楼层依据出现次数较多的阻尼器数目、接近平均数和阻尼器总数量为15 的原则，双目标优化算法在X向与Y向的最终阻尼器竖向布置如表4 所示。相比于逐层逼近法，双目标优化算法的目标函数值与其几乎相同，侧面说明该算法在阻尼器竖向布置上的优化能力较好。相比于工程师设计，双目标优化算法的目标函数值f1、f2均小于工程师设计，说明该优化算法在阻尼器数量固定的前提下能辅助工程师进行竖向布置修正，充分发挥阻尼器的减震性能，减小各楼层的最大加速度与最大层间位移角。

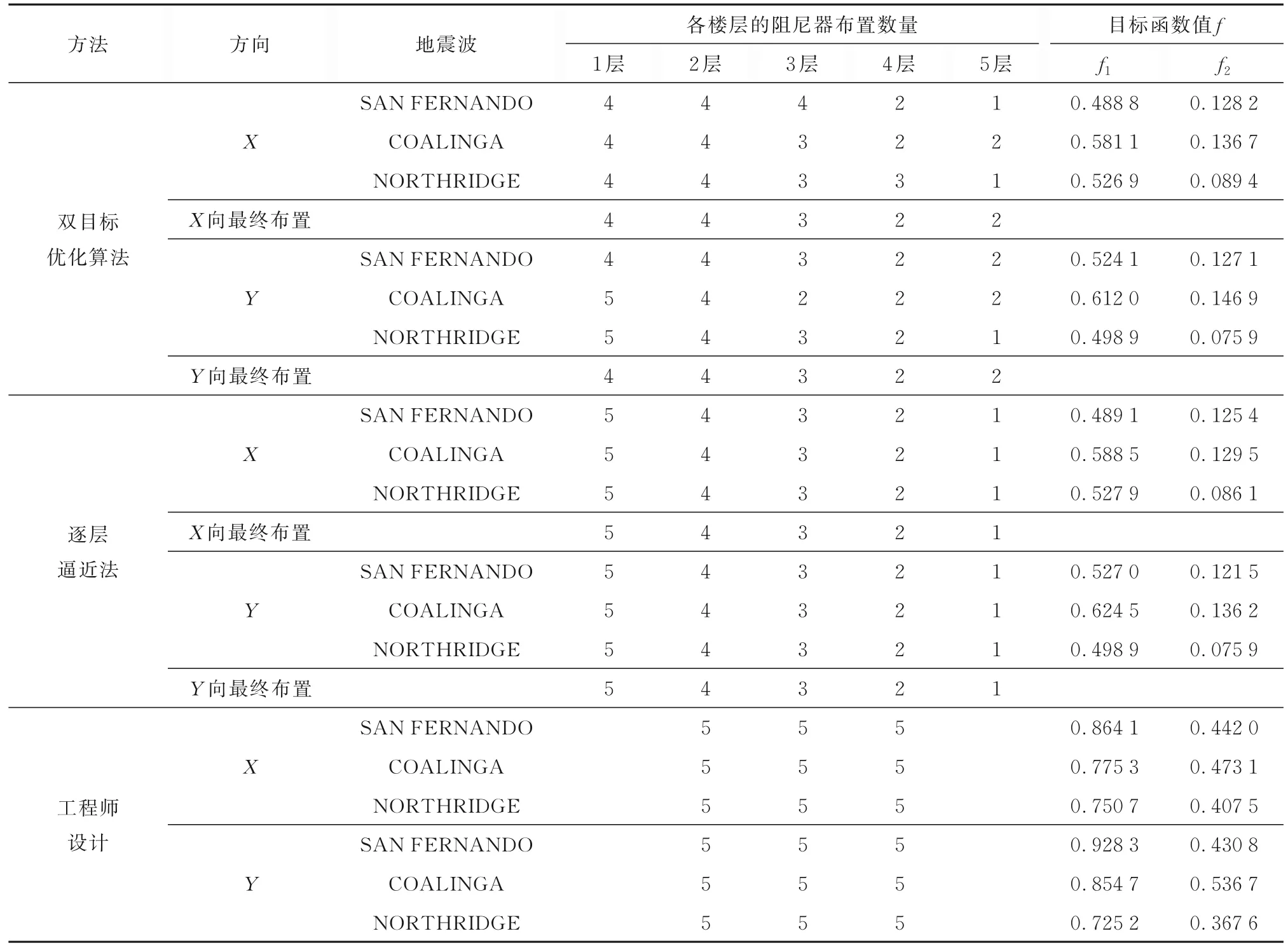
表4 案例一的阻尼器布置方案与目标函数值Table 4 Damper layout schemes and objective function values of case one

与原结构相比，采用不同阻尼器竖向布置方法得到的结构最大层间位移角和最大楼层加速度均有所降低。对于最大层间位移角，双目标优化算法与逐层逼近法的竖向布置均能满足减震目标1/200的要求，而工程师设计不能满足减震目标，如图7 所示。主要原因在于工程师设计的首层与顶层未布置阻尼器，导致其首层、顶层成为楼层薄弱处，层间位移角未能减小至减震目标。对于最大楼层加速度，双目标优化算法与逐层逼近法的最大楼层加速度均小于减震目标5 m/s2，但工程师设计未能达标，如图8 所示。这是因为首层、顶层为薄弱层，导致首层与顶层的最大楼层加速度未减小，甚至增大。

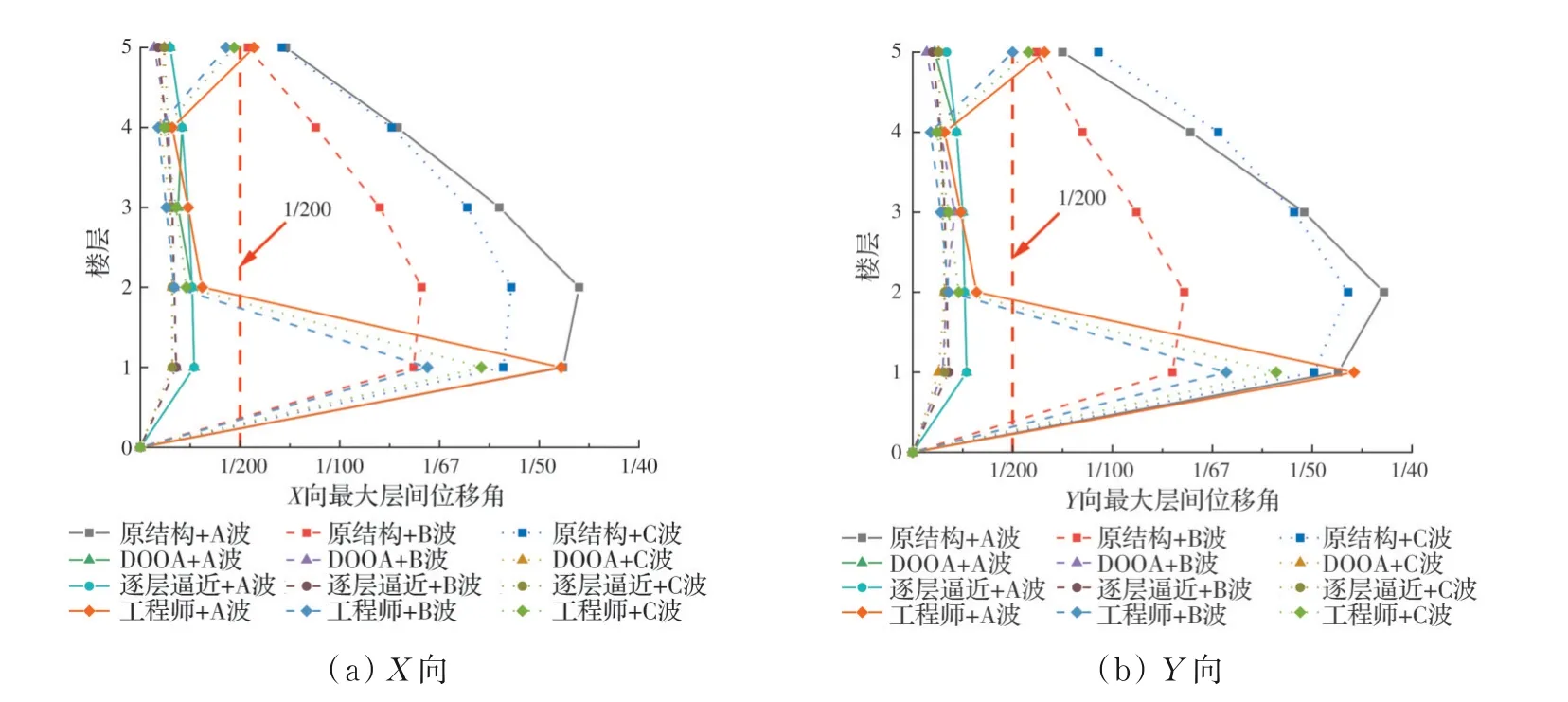
图7 最大层间位移角包络图Fig.7 Envelope diagram of maximum inter-story displacement angle

图8 最大楼层加速度包络图Fig.8 Envelope diagram of maximum floor acceleration

4.1.3 阻尼器平面优化布置

在双目标优化算法确定的案例一阻尼器竖向布置的基础上，分别让训练好的生成对抗网络模型和工程师进行阻尼器平面布置，并以工程师设计的阻尼器平面布置为目标设计。案例一的目标设计与生成设计如图9、图10 所示。

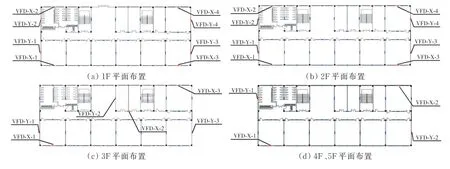
图9 案例一目标设计Fig.9 Objective design of case one

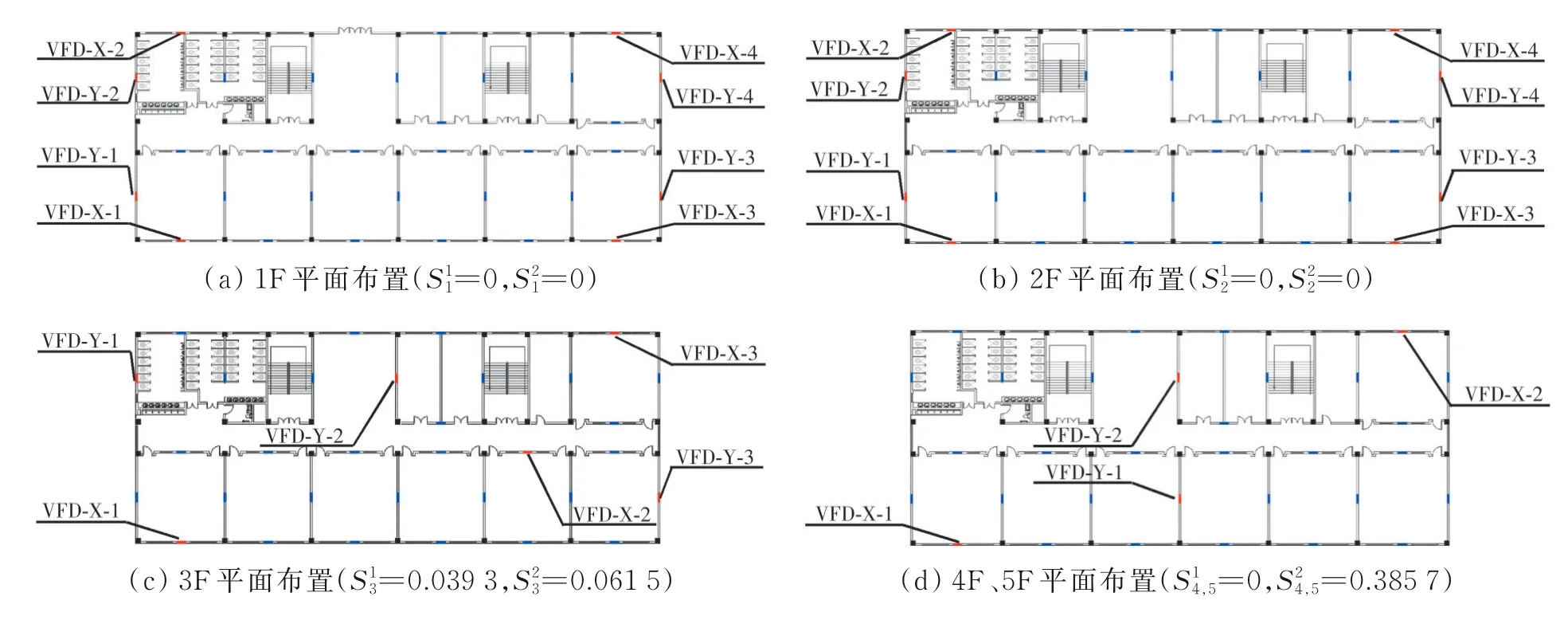
图10 案例一生成设计Fig.10 Generative design of case one

在该工程案例中，生成设计的相似性综合评价值为E1=0.05，各楼层的质心差异度和分散性差异度见图10。由于相似性综合评价E比较接近0，生成设计与工程师设计具有较高的相似度。

4.2 工程案例二

4.2.1 结构模型

某6 层钢筋混凝土框架结构办公楼，首层层高6 m，标准层层高4 m，总高26 m；柱截面为650 mm×650 mm，边主梁截面为600 mm ×800 mm，内主梁截面为400 mm×700 mm，次梁均为300 mm ×600 mm，结构平面布置如图11所示，各楼层的质量和刚度见表5。抗震设防烈度为8度（0.3g），地震分组为第3组，场地类别为Ⅱ类，设防类别为乙类。

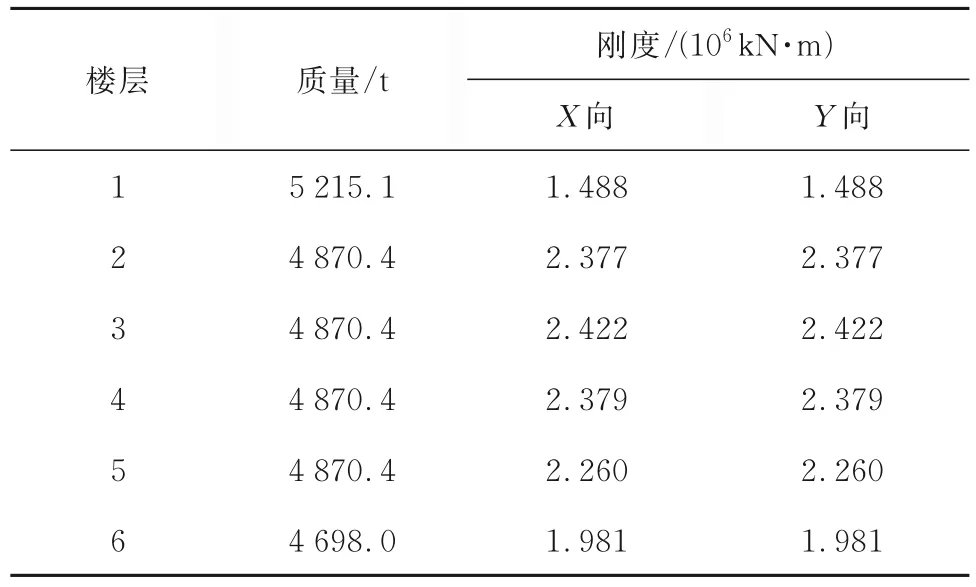
表5 某6 层RC 框架结构的质量和刚度Table 5 The mass and stiffness of a six story reinforced concrete frame structure

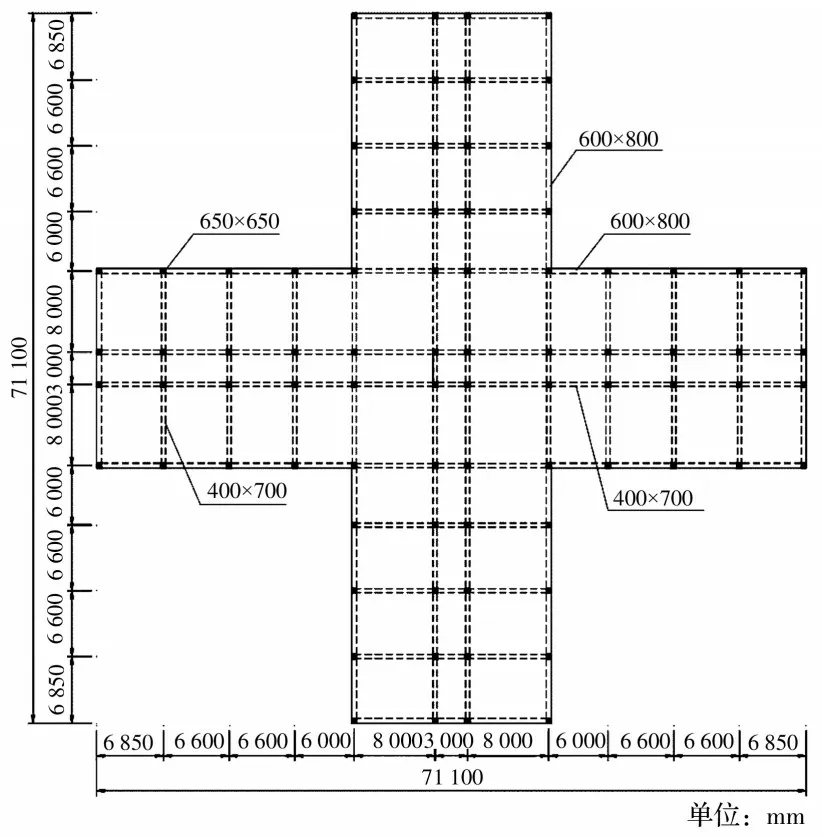
图11 案例二框架结构平面布置Fig.11 Plane placement of frame structure for case two

依据工程师试算，案例二需安装48 个黏滞阻尼器，具体阻尼器参数见表6。在工程师设计的基础上，优化阻尼器布置位置，提升框架结构的抗震性能，使其层间位移角和楼层加速度满足一定的减震目标，具体减震指标为：在8 度罕遇地震作用下，层间位移角控制在1/200 以下，楼层加速度控制在6 m/s2以下。

表6 阻尼器参数Table 6 The parameters of dampers

4.2.2 阻尼器竖向优化布置

根据案例二场地特征周期Tg2=0.5 s 与结构基本周期Ta2=1.27 s，选取出与其周期相近的3 条地震 动：SAN FERNANDO（台 站110）波、SAN FERNANDO（台站160）波、NORTHRIDGE（台站5366）波，分别记为A 波、D 波、C 波，并将各地震波的峰值加速度调整至510 cm/s2。

案例二结构在X向与Y向的质量、刚度和平面布置完全相同，故在各楼层两主轴方向上布置同等数量的阻尼器。同一楼层依据出现次数较多的阻尼器数目、接近平均数和阻尼器总数量为24 的原则，双目标优化算法在X向与Y向的最终阻尼器竖向布置如表7 所示。在3 条地震动作用下，双目标优化算法的目标函数值与逐层逼近法、工程师设计非常接近，但其f1值均优于逐层逼近法，f2值均优于工程师设计，再次说明该算法在阻尼器竖向布置上的有效性、合理性。而且，布置的阻尼器集中于中下部楼层，符合以往的阻尼器布置经验。

表7 案例二的阻尼器布置方案和目标函数值Table 7 Damper placement schemes and objective function values of case two

与原结构相比，不同阻尼器布置方法的最大层间位移角和最大楼层加速度均有所降低。对于最大层间位移角，双目标优化算法与逐层逼近法的竖向布置均能满足减震目标1/200 的要求，而在A 波作用下，工程师设计的1、2 层的层间位移角未能满足减震目标，如图12 所示。主要原因在于首层的楼层剪力较大和阻尼器数量不足，导致首层的层间变形过大，使其层间位移角未能满足减震目标。对于最大楼层加速度，双目标优化算法、逐层逼近法和工程师设计的最大楼层加速度均小于加速度减震目标6 m/s2，如图13 所示。

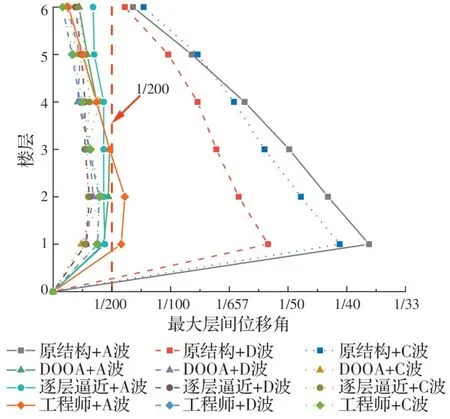
图12 最大层间位移角包络图Fig.12 Envelope diagram of maximum inter-story displacement angle

图13 最大楼层加速度包络图Fig.13 Envelope diagram of maximum floor acceleration

4.2.3 阻尼器平面优化布置

在双目标优化算法确定的案例二阻尼器竖向布置的基础上，分别让训练好的GAN 模型和工程师进行阻尼器平面布置，并以工程师设计的阻尼器平面布置为目标设计。案例二的目标设计与生成设计如图14、图15 所示。

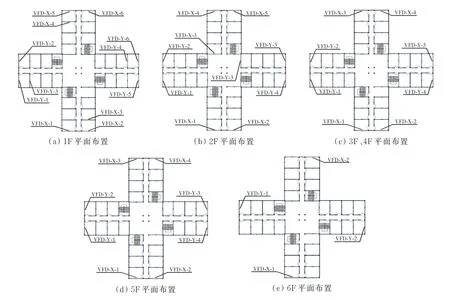
图14 案例二目标设计Fig.14 Objective design of case two

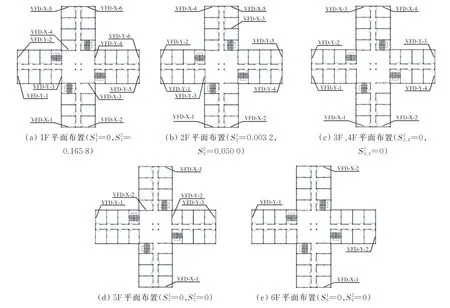
图15 案例二生成设计Fig.15 Generative design of case two

在该工程案例中，生成设计的综合相似性评价值为E=0.02，各楼层的质心差异度和分散性差异度见图15。由于相似性综合评价E非常接近0，生成设计与工程师设计具有较高的相似度。虽然生成设计与目标设计的阻尼器平面位置不完全相同，但阻尼器质心与分散性相同，导致其实际减震效果完全相同，例如该案例的5F、6F。

4.3 双目标优化算法效率分析

阻尼器智能布置在竖向布置上耗时占比最大，对算法效率影响最大，故只针对双目标优化算法进行效率分析。

在EI Centro 地震波作用下，以案例二的标准层平面布置、阻尼器参数为依据，开展2、4、6、8、10 和12 层框架结构的双目标优化算法效率分析，并与逐层逼近法、工程师设计进行对比。采用双目标优化算法、逐层逼近法和工程师设计对框架结构分别进行5 次设计，取其所用平均时间，其统计结果如表8所示。

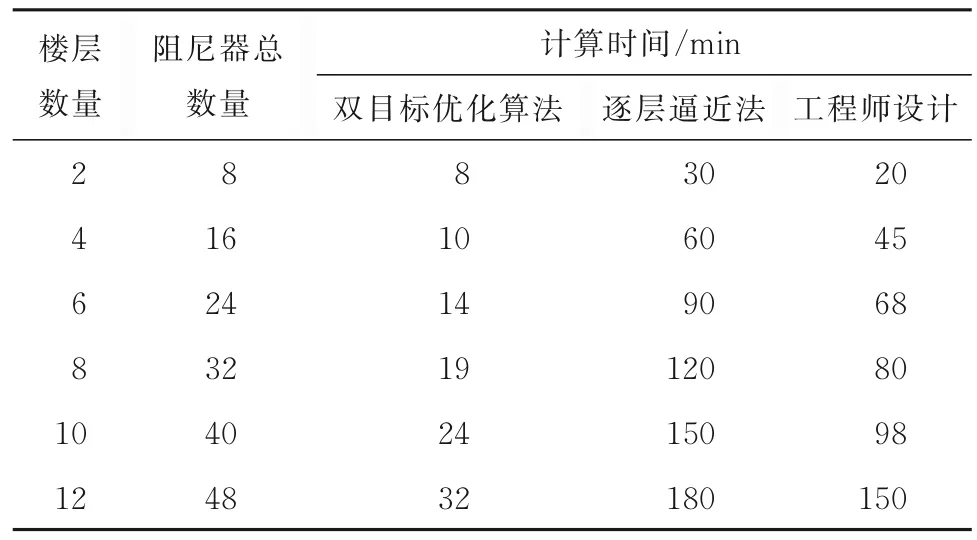
表8 计算时间Table8 The time of calculation

由表8 可知，双目标优化算法在阻尼器竖向布置上所用时间随楼层数量与阻尼器数量增大而增长，且远小于逐层逼近法与工程师设计。双目标优化算法计算时间较短，分析原因主要有两点：1）算法内嵌入了楼层地震响应有限元程序，可快速计算最大楼层加速度、最大层间位移角，避免了调用有限元软件计算速度慢的问题；2）调整双目标优化算法的种群数量为5，迭代次数为100，既能保证优化结果较好，又能极大降低优化计算所用时间。而逐层逼近法计算时间最长，主要原因在于需要工程师使用有限元软件迭代计算并确定每个阻尼器所在楼层，直至布置完所有阻尼器。工程师设计所用时间位于两者之间，是由于工程师可以利用积累的减震设计经验减少迭代次数，从而较快地完成阻尼器竖向布置。

4.4 平面布置评价指标临界值α

目前，尚未明确平面评价指标E的临界值，即：当E小于某个临界值时，生成设计与目标设计相似度较高，平面布置可靠，结构力学性能较好。因此，以抗扭力学性能的优劣来搜寻平面布置评价指标临界值α。针对阻尼器平面布置的相似性综合评价指标E的临界值，以工程案例二为试算模型，基于工程师设计的阻尼器竖向布置，开展12 种不同平面布置的扭转力学分析。值得说明的是，虽然工程案例采用的黏滞阻尼器在理论上不提供刚度，但在实际工程中存在一定的刚度，会对结构的扭转产生影响。经过试算得到不同平面布置方式下的框架结构扭转周期比和考虑偶然偏心作用下的X、Y方向最大位移比，以及相似性综合评价E值，如表9 所示。其中，考虑偶然偏心的位移比采用规范反应谱方法进行计算，偶然偏心取0.05[19]。已知工程师设计的扭转周期比为0.785 9，最大扭转位移比均值为1.173。

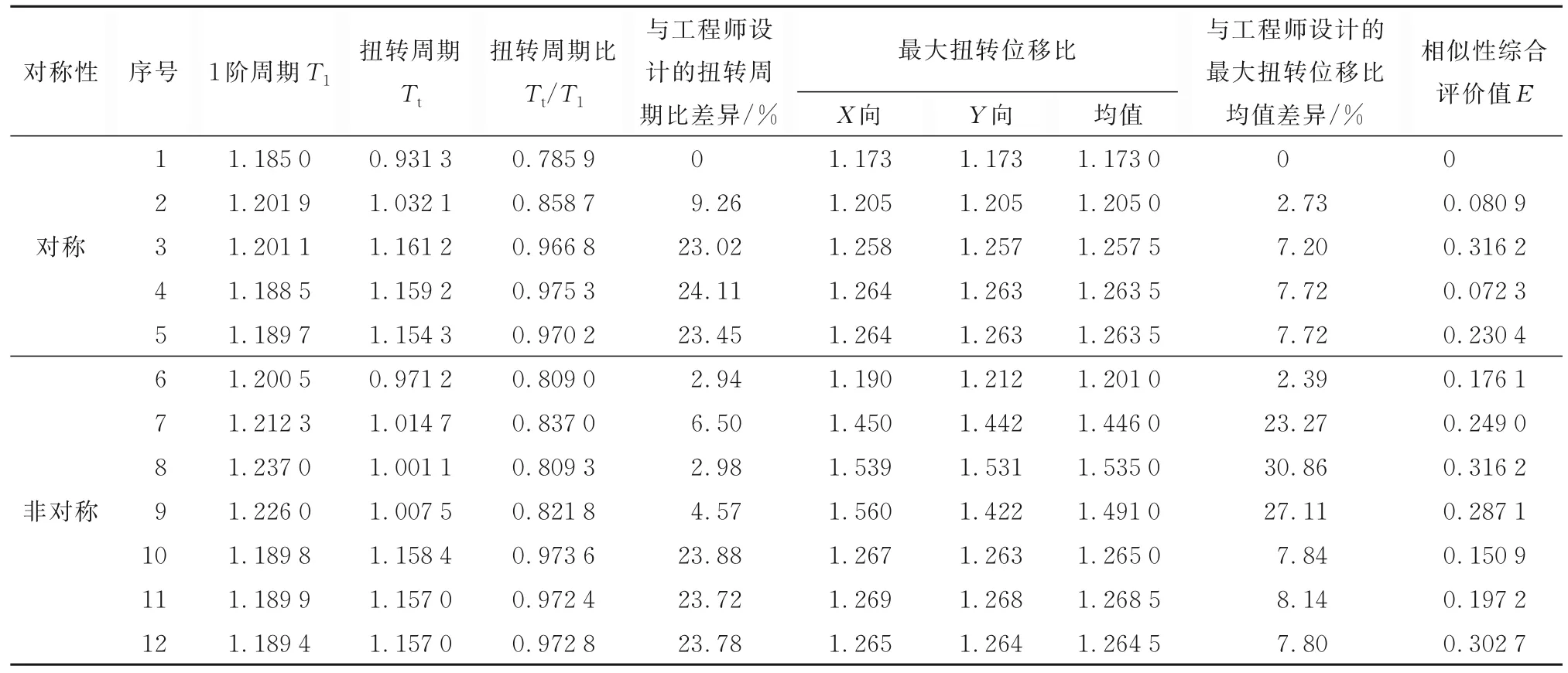
表9 结构扭转周期比、位移比和E 值Table 9 The torsion period ratio,displacement ratio and E value of the structure

将12 种平面布置方式的分析结果绘制在图16中，可以看出：当相似性差异度综合评价E＜α=0.1时，可保证生成设计与工程师设计的扭转周期比差异在10%以内，最大扭转位移比差异在5%以内，且扭转周期比、扭转位移比分别满足规范要求的0.9、1.6。案例一、案例二的相似性差异度综合指标E均小于0.1，间接说明生成对抗网络生成的平面布置满足结构抗扭力学性能要求。

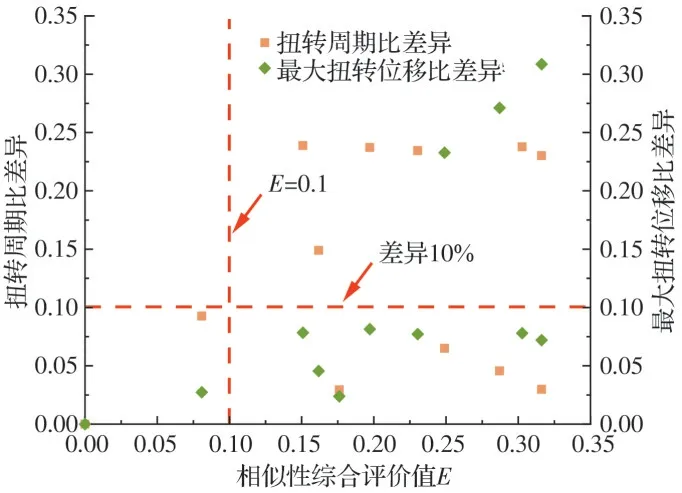
图16 力学性能与评价指标相关性Fig.16 The correlation between mechanical properties and evaluation indexes

5 结论

基于双目标优化算法和生成对抗网络算法进行阻尼器竖向和平面布置的智能设计，并进行了工程应用，得到以下结论。

1）基于结构地震响应公式与双目标优化算法进行阻尼器竖向智能布置。在推导出线性黏滞阻尼减震结构弹性阶段地震响应公式后，采用双目标优化算法求解优化目标函数值f1、f2最小时的各楼层阻尼器数量，可实现线性黏滞阻尼器的竖向智能布置。

2）基于生成对抗网络进行阻尼器水平智能布置。在完成阻尼器竖向布置后，即在确定各楼层阻尼器数量后，采用生成对抗网络算法，对其生成器进行训练，利用生成器完成阻尼器平面智能布置，可实现线性黏滞阻尼器的平面智能布置。

3）对两个框架结构减震设计案例进行双目标优化算法与生成对抗网络的工程应用。通过在竖向布置上同逐层逼近法、工程师设计进行对比，在平面布置上同工程师平面布置进行对比，可知：双目标优化算法生成的阻尼器竖向布置方案满足减震目标、生成对抗网络算法生成的阻尼器平面布置方案均与工程师的布置方案基本一致，直接说明了所提智能设计方法在阻尼器布置上的有效性。