基于多种群遗传算法的钢框架结构优化设计

2024-04-11周俊文刘界鹏

土木与环境工程学报 2024年1期

周俊文,刘界鹏

（重庆大学土木工程学院；山地城镇建设与新技术教育部重点实验室，重庆 400045）

中国位于地震多发带，受地震作用的影响，大量建筑物被损毁，造成了巨大的经济损失和人员伤亡[1-3]。据建筑业发展报告统计，2021 年上半年，中国建筑业企业完成建筑业总产值119 843.55 亿元，同比增长18.85%，呈现出蓬勃向上的发展趋势，建筑结构的安全性和经济性成为重要的关注点。因此，研究高效的建筑结构设计方法，对保证建筑行业的快速发展具有重要的现实意义。

传统的建筑结构设计方法主要依赖PKPM 等设计软件的力学计算分析结果，凭借专家经验对结构进行人为调整，包括合理的构件布置和截面取值等，使其满足相关规范的要求，以实现优化设计，在保证结构安全性的同时降低建筑材料成本[4-8]，该方法受人为主观因素的影响较大且耗时耗力，已无法满足建筑行业快速发展的需求。以智能化方法实现结构的自动建模分析和优化设计，能有效改善传统结构设计效率低下的问题，并保证优化后结构的经济有效性[9-12]。

与传统的混凝土结构、砌体结构相比，钢框架结构具有轻质高强、延性好、结构形式简单、施工方便等优点，应推广其在地震区的应用[1]，近年来，在钢框架结构的智能优化设计方面已有大量学者进行了相关研究。Degertekin 等[13]考虑截面选型和位移约束，采用和声搜索算法对钢框架进行了优化设计，降低了钢框架的重量。Gholizadeh[14-15]采用智能算法对平面钢框架结构进行了优化设计，包括蝙蝠算法和海豚回声算法，研究了结构尺寸的优化，实现了结构总质量的降低，研究了剪力墙位置的优化，得到了最优布局。Talatahari 等[16]采用基于差分进化的鹰策略算法，Çarbaş[17]采用基于生物地理学的优化算法，Kaveh 等[18]采用先进的充电系统搜索算法对钢框架结构进行优化，优化后的结构能够满足约束限值的要求，其材料总成本得到了有效地降低。智能算法已在结构优化的研究中有了广泛的应用，在每次优化过程中，需要首先对算法参数进行相应的设置，当其取值不合理时，容易会引起算法的收敛性和优化结果的优异性等问题，造成计算量大、耗时长、结果不理想、随机性强等后果，如遗传算法中的变异概率，当其设定较大时，容易破坏原有优秀个体的基因，当其设定较小时，可能使优化陷入局部最优解而过早收敛。在单次优化过程中，引入多种群的概念，每个种群设置不同参数值而表现出不同的优化性能，通过信息共享来进行不同种群间的交流，从而发挥多种群算法的综合性能优势，能够有效提高搜索能力，降低优化结果对参数设置的依赖性[19-20]。基于多种群思想的算法在优化问题中存在一定的优势，已应用到兵工、计算机等领域[21-22]，然而其在土木工程领域的应用仍有限。对于建筑结构设计而言，优化问题比较复杂，涉及非凸性、非线性、变量离散性、局部最优解众多等，优化对象存在较大的结构差异和较强的构件相互作用，且优化结果和收敛性高度依赖于算法的更新机制和搜索能力，因此，在实现高效的结构优化设计方面，该算法的适用性仍有待研究。

目前，中国正在大力推进经济有效结构的发展，以最小的资源和成本，造出外观美、空间分布合理并满足安全性要求的建筑物，实现资源的最大化利用和经济性。笔者以遗传算法为基础，通过多种策略对其进行改进并引入多种群思想，将其应用于钢框架结构的优化问题中，以验证方法的有效性，旨在为钢框架结构的优化设计提供参考。

1 优化问题

1.1 优化对象

研究对象为4 跨10 层的平面钢框架结构，截面为工字型钢，钢号为Q235，跨度为4 m，层高为3 m，从下往上总共分为3 个标准层，其中1～4 层为标准层1，5～7 层为标准层2，8～10 层为标准层3。考虑荷载工况为1.3 倍重力荷载代表值+1.3 倍水平地震作用，前者由恒载4.5 kN/m2（楼面恒载2 kN/m2+楼板自重2.5 kN/m2）与活载2 kN/m2计算得到，将其等效为竖向线荷载作用在梁上；采用底部剪力法计算等效水平地震作用，地震设防烈度、地震动设计特征周期、地震影响系数最大值、阻尼比分别取为6度、0.35 s、0.04、0.04，将其等效为水平荷载作用到每一层柱顶节点上。通过MSC.Marc 软件建立钢框架结构的有限元模型，见图1，梁柱构件均采用梁单元，结构底部和梁柱节点均为刚接。由于本文旨在研究智能算法在结构优化设计中的有效性，而优化过程最耗时部分为结构的有限元分析，因此，为了节约计算时间，仅考虑弹性分析，钢材密度取为7 850 kg/m3，弹性模量取为206 GPa。

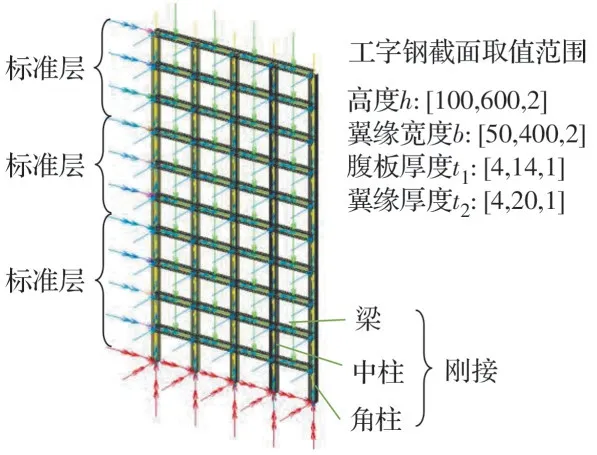
图1 钢框架结构的有限元模型Fig.1 Finite element model of steel frame structure

1.2 约束条件

根据《建筑抗震设计规范》（GB 50011—2010）[23]和《钢结构设计标准》（GB 50017—2017）[24]规定，在钢框架的优化设计中考虑以下结构约束条件。

最大层间位移角约束

式中：dri为第i层的层间位移角；dru为最大层间位移角限值，取为1/250；ns为楼层数量。

应力约束

式中：σi为第i组构件的最大应力；σu为钢材的屈服强度值，取为235 MPa；ng为构件的组数。

稳定性约束

式中：Ei、Ai、Wxi、Wyi、Ni、Mxi、Myi分别为构件i的材料弹性模量、截面面积、x向毛截面模量、y向毛截面模量、轴力、x向最大弯矩、y向最大弯矩；λxi、λyi分别为构件i对x轴、y轴的长细比；λxi、λyi为构件i的截面塑性发展系数；φxi、φyi分别为构件i对x轴、y轴的轴心受压整体稳定系数；βmxi、βmyi为构件i按《钢结构设计标准》（GB 50017—2017）第8.2.1 条弯矩作用平面内稳定计算采用的等效弯矩系数；βtxi、βtyi为构件i按《钢结构设计标准》（GB 50017—2017）第8.2.1 条弯矩作用平面外稳定计算采用的等效弯矩系数；f为构件i的材料强度设计值；η为截面影响系数，取为1；nm为构件的总数。

尺寸约束

计算后约束：

式中：hbi、tbwi分别为第i组框架梁的腹板高度和腹板厚度；ρi为第i组框架梁的最大轴压比；λci为第i组框架柱的长细比；λu为框架柱最大长细比限值，取为100ε，ε为钢号修正系数。此类约束需要在有限元分析后由其结果计算得到，包括框架梁的腹板宽厚比和框架柱的长细比。

计算前约束

式中：bci、hci、tcfi、tcwi分别为第i组框架柱的翼缘外伸部分宽度、腹板高度、翼缘厚度、腹板厚度；bbi、tbfi分别为第i组框架梁的翼缘外伸部分宽度、翼缘厚度，ngc、ngb分别为框架柱、框架梁的组数。此类约束可以在进行有限元分析前计算得到，包括框架柱的翼缘外伸部分和腹板宽厚比、框架梁的翼缘外伸部分宽厚比。

2 优化方法

2.1 设计变量

如图1 所示，钢框架结构总共设有3 个标准层，将每个标准层中的构件划分3 组，包括角柱、中柱和梁，总共有9 组构件，每组构件设置4 个参数，包括工字型钢截面的翼缘宽度b、总高度h、腹板厚度t1、翼缘厚度t2，记为（b、h、t1、t2），单位为mm，因此，该优化问题中总共考虑36 个设计变量，变量的取值范围见表1。

表1 设计变量取值范围Table 1 Range of design parameters

2.2 目标函数

以结构的钢材总质量最小化为目标函数，包括所有的框架梁柱构件，其数学表达式为

式中：li分别为构件i的长度。

采用外部罚函数法计算惩罚后的结构总质量，构造辅助函数对约束条件进行处理，其表达式为

通过辅助函数，将约束条件考虑到目标函数中，得到惩罚后的目标函数，称为伪目标函数，其数学表达式为

式中：gi为约束条件值，由式(1)～式(6)计算得到；n为约束条件总数。

当结构满足所有的约束条件时，式（12）第2 项为0，伪目标函数等于结构总质量；当结构存在约束超限的情况时，式（12）第2 项将远大于0，伪目标函数大于结构总质量。因此，伪目标函数值越小，则结构更好，其既能满足所有的约束条件，又能实现经济性。

伪目标函数是一项考虑结构原始总质量和所有约束条件的综合指标，可以将有强约束的结构优化设计问题转换为无约束问题，通过种群个体函数值之间的对比，能够反映出结构违反约束条件的程度、超限数量、材料质量和结构相对优劣等信息，以实现对个体的比较选择。

2.3 优化算法

以遗传算法为基础，引入多种改进策略和多种群思想，结合结构和设计变量特征，基于规范要求对钢框架结构进行优化设计，旨在说明多种群遗传算法的有效性。采用的所有算法都具有相同的种群初始化、适应度评估步骤，在设计变量生成和更新时都采用了基于约束的策略，将先对其进行统一描述。

基于约束的策略见图2。遗传算法是一种随机性较强的算法，在初始化和迭代过程中生成种群时不具有方向性，通常存在新个体无法满足约束条件或原本满足要求的个体在变量更新后出现超限的情况，这会增加无效个体（存在超限情况的个体）的数量，从而导致计算时间的增加。为了减少该情况发生的可能性，以构件组为单位，采用基于约束的策略来改善该问题，仅针对计算前约束条件。在初始化过程中或在迭代过程中通过交叉、变异操作后，当有新个体生成时，遍历每个构件组，均通过式（7）～式（9）对其截面参数进行相关验算，当满足要求时，该构件组生成有效，否则重复进行相同操作，直至满足要求为止，为了避免某些构件组始终无法满足要求而陷入死循环的情况，设置最大重复操作的次数，在超过30 次后，将该构件组的4 个参数在取值范围内重新随机生成，直到满足要求。该策略将应用于包括种群初始化、交叉、变异、重生成等所有会生成新个体的步骤中。

图2 基于约束的策略Fig.2 Constraint-based strategy

种群初始化。个体的所有设计变量在相应的取值范围内随机选择，以构件组为单位，采用基于约束的策略生成最终个体，最大限度地保证初始种群在可行域内均匀分布和算法的全局搜索能力。

适应度评估。采用式（12）计算每个个体的伪目标函数值，进而得到其适应度。

2.3.1 遗传算法

遗传算法（Genetic Algorithm，GA）是基于大自然中生物体进化规律，模拟达尔文生物进化论的自然选择法则和遗传学机理的生物进化过程思想的一种优化算法，具体为将优化问题以基因的形式对种群中所有个体进行编码，通过自然选择、遗传和变异过程实现新种群的更新迭代，最终获得适应性高的个体，即最优个体，该方法已被广泛应用于机器学习、信号处理、组合优化等领域。该算法的主要流程（见图3）如下。

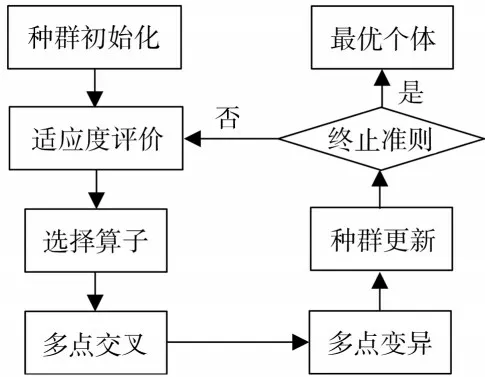
图3 遗传算法流程Fig.3 Process of genetic algorithm

1）个体编码。采用实数编码方式将求解问题转换为可供遗传算法进行后续操作的带有数据信息的染色体或个体，建立问题解空间和算法参数搜索空间的映射关系。

2）选择算子。根据遗传算法中“适者生存”的思想，从上一代种群的适应度选择出优质个体作为交叉和变异操作的基础。采用轮盘赌策略对个体进行选择，即通过计算所有个体的适应度，其值越高，则被选择的概率越大。

3）交叉算子。在荷载作用下，结构构件具有较强的相互作用关系，存在着荷载的分配问题，如应力不仅与该构件的截面尺寸相关，还与其他构件的刚度以及分配的荷载相关，若在所有设计变量之间采用多点交叉，容易导致原本满足应力要求的构件发生超限的情况，使算法的收敛速度降低等问题。为了提高算法的性能，采用基于构件层次的多点交叉策略，即在每一组构件的4 个参数中随机选择一个点位进行交叉，突出相同构件组之间父代特性的继承和遗传。

4）变异算子。与交叉算子相似，采用基于构件层次的多点变异策略，即在每一组构件的4 个参数中随机选择一个点位，在其取值范围内随机生成，提高对构件组的局部搜索能力，增加种群的多样性并避免“早熟”现象的发生。

5）终止准则。设置最大迭代次数和最优解保持在误差范围内的最大连续次数，当满足任意一种情况时，优化过程终止，输出最优解。

2.3.2 改进遗传算法

经典遗传算法存在着一些弊端，在基于轮盘赌策略的选择操作中，迭代后期的个体差异较小，由于适应度相近较难选择出真正的优质个体，在交叉和变异操作中，概率固定且缺乏搜索方向的引导，对设计变量的取值扰动较大，容易破坏构件层次的优质基因，使算法的局部搜索能力降低，整体未设置精英保留策略，可能造成优质个体基因的浪费。因此，考虑采用适应度尺度变换、基于方向的交叉算子、非均匀变异算子、自适应概率、精英保留策略、重复项替代机制对其进行改进，称为基于方向的自遗传算法（genetic algorithm，DBAGA），其主要流程见图4。

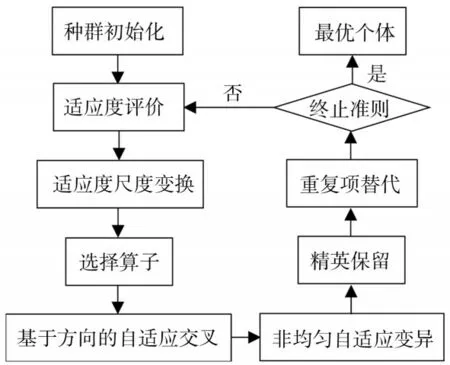
图4 DBAGA 算法流程Fig.4 Process of DBAGA

适应度尺度变换[25]。适应度对算法的收敛性有一定的影响，为了在优化初期对少数适应度较高的个体进行控制，降低其与其他个体的差异，以维护种群多样性，在优化后期适当放大个体之间的差异，提高优质个体的竞争性，采用线性尺度变换策略对适应度进行处理，其数学表达式为

式中：f、f ′分别为尺度变换前后的适应度值；a、b为系数，由式（14）～（15）计算得到，即尺度变换后的适应度平均值f ′ave和最大值f ′max应分别等于尺度变换前的适应度平均值fave和其指定倍数；c为最佳个体期望复制系数，一般取为1～2。

基于方向的交叉算子[26]。智能算法如粒子群算法中通常通过较优个体来引导种群中其他个体的搜索方向，从而使其向更好的方向移动，采用基于方向的交叉算子来实现，其数学表达式为

式中：、分别为第k次迭代中选择出的第i个和第j个个体；λ为步长，取为1；R1、R2为取值为[0,1]且与维度设计变量相同的随机数向量；D为和中较优个体与较差个体的向量差，即交叉方向。

非均匀变异算子[27]。通过基因位随机数替代可能导致优质个体被破坏，采用非均匀变异算子，仅在所选点位附近作一微小随机扰动，可以提高对重点区域的局部搜索，其数学表达式为

式中：x、xu、xl分别为基因位对应参数的当前取值、最大取值、最小取值，r为[0,1]的随机数；t为当前迭代数；T为最大迭代数；b为系数。

自适应概率。固定概率的设置会影响算法的性能，当其过大时，优质个体的基因被破坏的可能性变大，从而增加算法的随机性，当其过小时，会使搜索过程缓慢，陷入局部最优解，采用自适应概率可以改善该问题。根据适应度的不同，在交叉操作中，设置2 阶段概率[25]；在常见的2 阶段变异操作中，较大概率值通常较小，难以达到变异作用，为了增加种群的多样性，增加变异的可能性，设置3 阶段概率。当适应度低于设定适应度时，说明个体较差，采用较大的交叉和变异概率，当适应度高于设定适应度时，采用较小的交叉和变异概率，以自适应概率的方式增加个体的竞争，提高算法的收敛速度，其数学表达式为

式中：pc1、pc2分别为较大和较小交叉概率；pm1、pm2、pm3分别为较大、一般和较小变异概率。

精英保留策略[25]。为了避免精英个体的丢失，提高子代个体对父代个体优质基因的继承特性，将历史最优解保存并在每一次迭代过程中用于替代最劣解，可以有效保证最优个体不会被破坏，提高算法的收敛性，但同样存在某个局部最优解不易被淘汰而使优化过早收敛的问题，因此与重复项替代机制配合使用。

重复项替代机制[26]。由于算法的遗传特性，经过选择、交叉和变异操作后，种群中很可能存在重复个体，为了避免重复计算和降低优化时间，用变异后的精英个体来替代重复项，能够有效增加种群的多样性，同时提高对精英个体参数取值附近的局部搜索，改善因精英保留策略带来的过早收敛和陷入局部最优解问题。

2.3.3 多种群遗传算法

优化算法的性能和结果受到算法中参数的影响，如遗传算法中的交叉概率等，基于固定参数的优化随机性较强、鲁棒性较差，采用基于多种群的思想可以改善此类问题。在同一次优化中，同时生成多个初始种群或者将整体群体划分为多个子群体，每个子群体设置不同的算法参数，各自同时进行优化，在一定的迭代次数后，通过移民算子将各子种群在进化过程中出现的最优个体引入相邻的子种群中，实现种群之间的信息交换。该方法能够有效降低的单一种群算法的随机性和提高鲁棒性，减少对参数设置的依赖性。对上述GA 和DBAGA都进行多种群的设置，即多种群遗传算法（Multi Population GA，MPGA）和基于方向的多种群遗传算法（Direction-based MPGA，DMPGA），以MPGA为例进行说明，见图5。在多种群算法中，各参数值不固定，只给定各自的取值范围，在每次优化开始时随机得到。

图5 多种群遗传算法Fig.5 Multi population genetic algorithm

移民算子。在多种群算法中，将群体划分为一些子种群，通过移民操作建立子种群之间的相互联系并实现信息交流，具体步骤如下：设置子种群数、移民间隔（相邻两次移民的间隔迭代数）和移民率（每次被移民的个体数量）；每个子种群按一定的模式（即独立优化器，在图5 中为GA）分别进行独立优化；当迭代次数满足移民间隔时，相邻子种群进行有序的移民操作。如设置子种群数为4，移民间隔为5，移民率为1，则将群体划分为4 个子种群，每个子种群进行独立优化，每5 次迭代时，用子种群1 中历史最优的1 个个体替换子种群2 中当代最差的1个个体，以此类推，按顺序完成所有子种群间的移民操作（2→3，3→4，4→1）。

2.4 自动优化过程

结构体系的自动优化设计过程主要包括结构的有限元分析和智能算法的迭代更新两步，搭建优化算法框架，通过MSC.Marc 有限元软件完成对初始化种群的力学分析，基于Python 二次开发技术对结构的计算结果进行提取和整理，得到个体的适应度，再由优化算法生成新一代种群，基于参数化建模方法和智能算法实现结构设计的反复计算分析和自动寻优过程，见图6。为了节约结构分析时间，利用多核CPU 设置并行计算。

图6 结构自动优化设计过程Fig.6 Automatic structural optimization design process

采用4 种算法对钢框架结构进行优化，各进行20 次优化，在优化过程中，各算法的参数设置保持不变，具体取值见表2。在2 种单种群算法中，因试算后发现种群规模设置较小时会出现过早收敛情况且优化结果不理想，故均设置为100；在2 种多种群算法中，移民算子均设置为每1 次迭代后进行相应操作，子种群均设置为5 个且每个子种群10 个个体。

表2 算法参数设置Table 2 Parameter setting of algorithms

3 结果分析

钢框架结构不同算法的优化曲线和计算结果见图7、图8 和表3。对于GA，20 次优化后的结构均能满足所有的约束条件，但最优解呈现出较强的离散性，其标准差为1.79 t，其中，最优解和最劣解分别为19.75、27.04 t，差值较大，达到7.29 t。从图7（a）中可见，大多数优化所需的分析次数在4 000 次左右，其中，有6 次优化所需的分析次数小于2 800次，计算成本较小，但在1 000 次分析后，大多数优化曲线进入平稳阶段且后期仅存在1～2 次下降，由此说明，该算法容易陷入局部最优解而过早收敛，局部搜索能力较差，这是因为其交叉和变异策略都是针对每个构件组的某一个随机的基因位进行的相关操作，不确定性较高，缺乏一个搜索方向的引导，容易造成优质基因被破坏。

表3 不同算法的优化结果Table 3 Optimization results of different algorithms

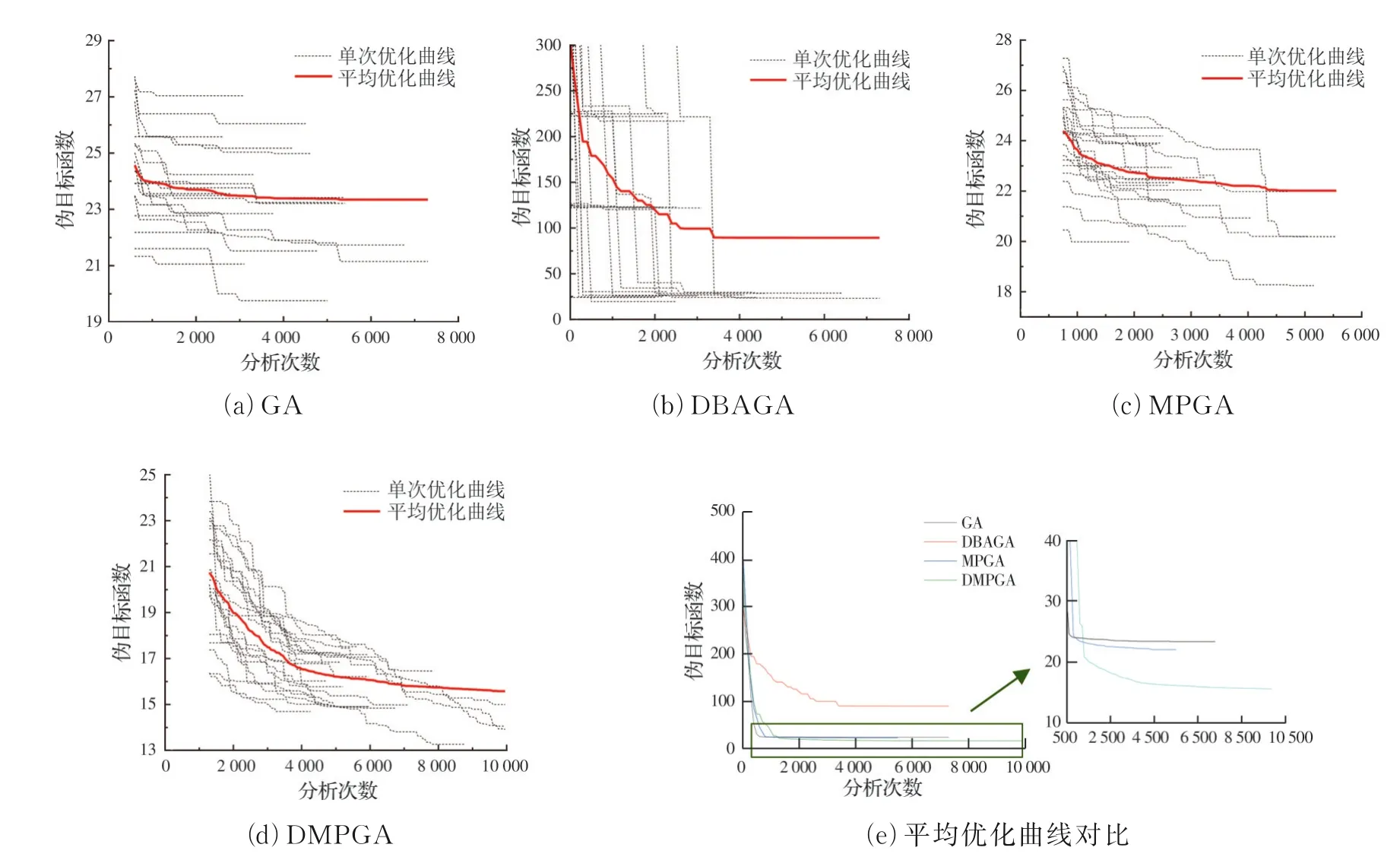
图7 不同算法的优化曲线Fig.7 Optimization curves of different algorithms

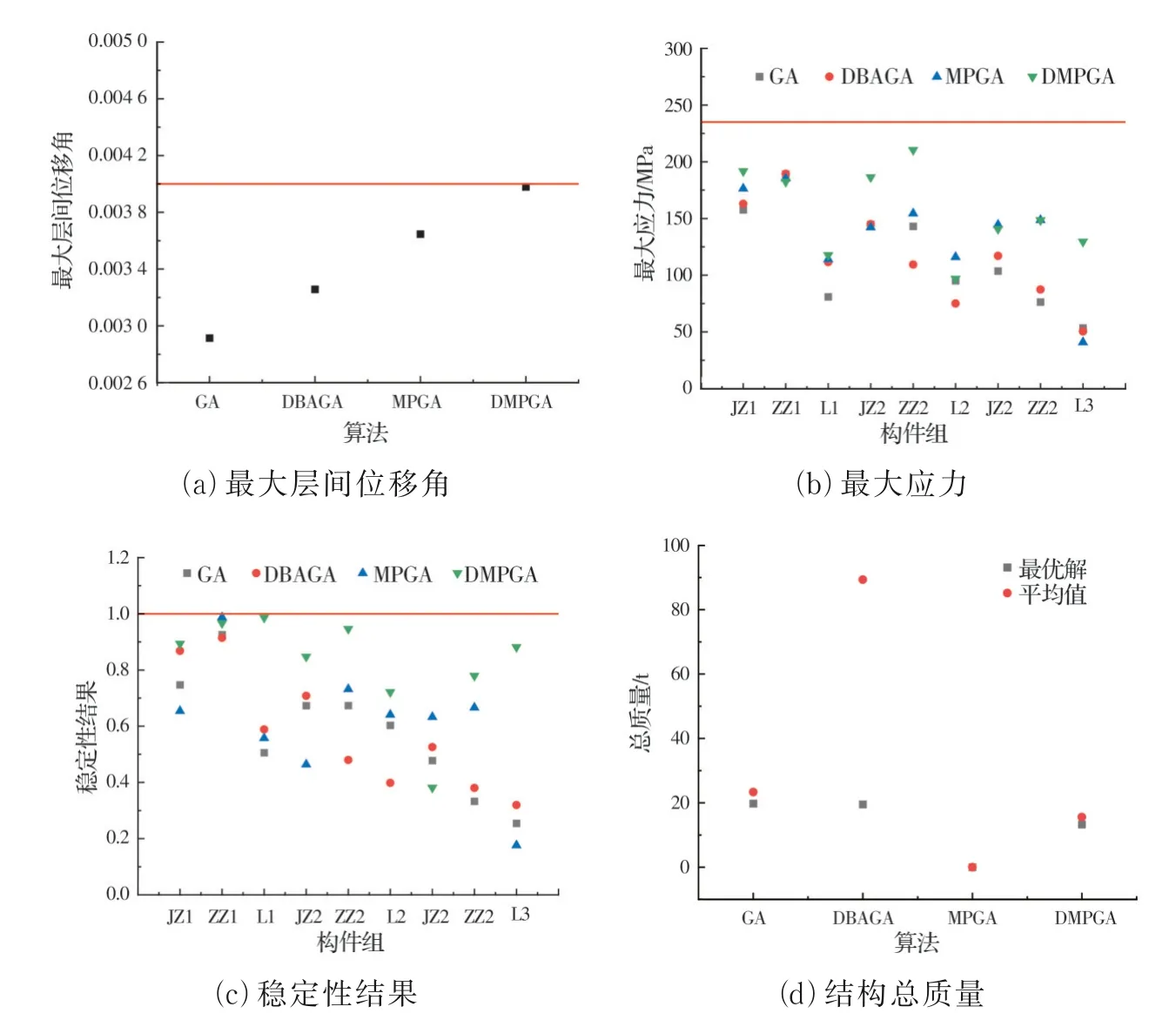
图8 不同算法的最优解计算结果Fig.8 Results of optimized solutions by different algorithms

对于DBAGA，优化后的结构中有8 次无法满足所有的约束条件，由于伪目标函数中考虑了约束条件的影响，因此，受多个最劣解的影响，优化结果的平均值和标准差均较差，分别达到89.35、89.11 t，在该算法参数的设置下呈现出较强的离散性和随机性。从优化所需的分析次数来说，有14 次算例小于3 000 次即可达到终止判别条件，计算代价较低，同样存在容易陷入局部最优解而过早收敛的问题。这是因为该算法的交叉策略是针对设计变量的所有维度，虽然通过较优个体向较差个体提供了搜索方向的引导，但受到算法参数的设置影响，如果交叉的两个个体都较差，其交叉后的子代个体则有较大可能无法得到好的改善，此外，在迭代后期，由于精英策略保留的历史最优个体将在种群中重要性增加，即使设置了重复项替代机制对该个体的重复项进行了变异且在其参数取值附近进行了局部搜索，但由于该个体本身质量较差且每一次迭代仅存在少数重复项，算法的局部搜索能力仍不易寻到更优质的解。

对于MPGA，优化后的结构均能满足所有的约束条件，最优解和最劣解分别为18.25、24.50 t，差值达到6.25 t，但除少数案例以外，其他优化结果相对集中且标准差仅有1.56 t，表现出较大的离散性，但优于GA。从图7（c）中可见，大多数优化所需的分析次数小于2 700 次，计算时间较短，在迭代前期能下降到接近最终解便进入到平稳阶段且后期出现下降的次数较GA 有所增加，说明算法的局部搜索能力较GA 更好，这是因为采用了多种群思想，部分改善了GA 存在的局部搜索能力较差的缺点。该算法的基础是GA，同样是基于构件组进行的交叉操作，在迭代过程中容易破坏较优个体，缺少搜索方向的引导，大多靠全局搜索来寻优，具有一定的随机性。

对于DMPGA，优化后的结构均能满足所有的约束条件，其中，最优解和最劣解分别为13.27、17.52 t，标准差仅有1.17 t，该算法的鲁棒性较好。从图7（d）可见，优化所需的分析次数大多集中于5 000 次左右，少数案例进行到了最大迭代次数才终止，受其影响，20 次优化所需的平均分析次数达到6 403 次，所有的优化曲线表现出较多次的下降，说明该算法的局部搜索能力较强。这是因为DMPGA设置了多个子种群，集合了多个不同参数设置且独立的DBAGA，极大地降低了单种群算法对其参数取值的依赖性，由于自适应概率和基于方向的交叉算子，每个DBAGA 都存在较差个体向较优个体前进的机制，即使其历史最优解的质量较差，但通过移民算子可以得到极大地改善。

由图7（e）可见，除DBAGA 之外，其他3 种算法优化后的结构均能满足约束条件。其中，GA、DBAGA 和MPGA 的平均优化曲线分别在约1 000、2 000 和1 500 次分析后下降到较低水平，优化前期的收敛速度较快，但随后基本保持平稳状态，此外，由表3 可见，3 种算法所需的平均分析次数分别为4 195、3 305、3 205 次，整体表现为局部搜索能力不足，存在早期陷入局部最优解而过早收敛的问题。相比之下，DMPGA 的平均优化曲线在1 000～3 000次分析中仍有较大幅度的下降，约6 000 次分析后进入稳定期，所需的平均分析次数为6 403 次，虽然远高于其他算法，但优化前期和后期均能表现出较好的搜索能力且最终得到的优化结果远好于其他算法，具体如下：从平均解来说，DMPGA 的结果为15.58 t，比GA、DBAGA、MPGA 的结果分别低33.3%、82.6%、29.2%；从最优解来说，DMPGA 的结果为13.27 t，比GA、DBAGA、MPGA 的结果分别低32.8%、32.1%、27.3%；从标准差来说，DMPGA 的结果为1.17 t，比GA、DBAGA、MPGA的结果分别低34.7%、98.7%、25.2%；从最劣解来说，DMPGA 的结果为17.52 t，比GA、DBAGA、MPGA 的最优解都小，分别低11.3%、10.3%、4.0%。因此，由于采用了并行计算技术，平均一次结构分析所用时间约为1～2 s，一次结构优化所需的总体计算时间约为1～4 h，耗时较短，DMPGA 在计算效率方面虽有不足和有待改进之处，但在可接受范围之内，此外，该算法在搜索能力和优化后结构的质量结果方面有明显的优势。

由图8 和表3 可见，不同算法的最优解都能满足约束条件，但最优结构的设计变量参数值和性能指标结果相差较大，这是因为每种算法都是基于遗传算法的思想，具有一定的随机性，即使结构总质量相近，但构件尺寸和结构性能仍存在较大差异。与GA 和DBAGA 相比，总体来说，基于多种群思想的MPGA 和DMPGA 最优解的结构性能指标更接近限值，两者相比，DMPGA 的结果更好，如最大层间位移角为0.003 98，基本等于限值1/250，多组构件的稳定性结果接近1，说明其优化后的结构更优，既能满足约束条件，又具有较小的总质量。

总体来说，DBAGA 比GA 的局部搜索能力更强，这是因为非均匀变异算子和重复项替代机制同时增加了种群的多样性和历史最优个体参数取值附近的局部搜索，但优化结果仍较差；基于多种群的算法能够有效改善基于单种群的算法的随机性和鲁棒性，通过多组不同参数设置降低了优化结果对其的依赖性，如在前面分析中提到的DBAGA 可能由于精英策略保留的个体质量较差而不易寻到更优质的解，但通过多种群机制的移民算子，能够有效建立起子种群之间多个历史最优解的联系，有效弥补了单种群算法的不足；与MPGA 相比，由于增加了基于方向的交叉算子能够引导较差个体向较优个体学习，DMPGA 具有更强的全局和局部搜索能力。