含内聚裂纹弹性体的能量释放率与断裂能*
2024-04-10安蕊梅侯永康李云峰段树金
安蕊梅, 侯永康, 李云峰, 段树金
(1. 石家庄铁道大学 土木工程学院, 石家庄 050043;2. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室, 石家庄 050043;3. 河北地质大学 城市地质与工程学院, 石家庄 050031;4. 山东科技大学 土木工程与建筑学院, 山东 青岛 266590;5. 山东华宇工学院 能源与建筑工程学院, 山东 德州 253034)
0 引 言
对于韧性材料、胶结材料等,当构件尺寸较小或裂纹尺寸较大时,其裂尖附近的塑性区或微裂区等非线性区域的大小往往不可忽略[1-2].自从Barenblatt[3]提出内聚裂纹模型(cohesive zone model,CZM)以来,裂纹尖端内聚区的内聚力与内聚区应变关系的表述就一直是断裂力学、特别是弹塑性断裂力学研究所关注的核心问题.由Dugdale[4]的解可以得到塑性区的长度或裂纹尖端张开位移,并为δ断裂判据提供了理论支撑,但这一解答只有在材料为理想刚塑性的假设下才能得到,因此只适用于低碳钢或塑料薄板受面内作用的断裂问题[5-6].文献[7]建立了基于黏聚区模型的纯Ⅱ型断裂的ENF试件裂纹扩展模型.
混凝土材料切口附近的非线性表现往往伴随着断裂过程区,其尺度大至分米甚至米级.Hillerborg等[8]将条形状的断裂过程区用虚拟裂纹来代替,提出了更具实用价值的虚拟裂纹模型(fictitious crack model, FCM),断裂能GF和拉应变软化曲线(即内聚区内聚力与内聚裂纹的关系曲线)被定义为材料断裂的两个控制参数,并应用于混凝土类材料的断裂分析.
内聚区模型具有普遍意义,适用于任何工程材料,但不同材料表现为不同的内聚区受力、变形特征,主要是不同的内聚区形状、尺度和本构关系.由于其解析的难度,目前绝大多数的研究都是采用试验测试数据结合有限元等数值方法进行迭代求解,内聚区的本构关系被假定为线性软化、双线性软化、指数函数等形式,或者内聚区的内聚强度被假定为恒定(Dugdale模型)、水压力、指数函数等形式[9-15].
段树金、中川建治等[16-17]把裂纹尖端的形状由椭圆形转换为尖劈形,提出了虚拟裂纹一般问题的解析方法.这种解消除了裂尖的应力奇异性,在全域都是解析的,从理论上为内聚区模型的发展和应用开辟了新途径.
为了避开裂纹尖端附近的复杂区域,从能量的观点出发,Rice[18]提出了J积分作为描述裂纹尖端应力应变场的参量.在线弹性情况下,J积分就是能量释放率G;对于Dugdale模型等虚拟裂纹模型,由于除线状的断裂过程区外,整个体都是弹性的,所以可以给出G=J.
在虚拟裂纹模型中存在两个裂纹尖端,即物理裂纹尖端和虚拟裂纹尖端,因此需要定义两个相应的能量释放率来描述两个裂尖的扩展[19].
本文将内聚区简化为虚拟裂纹,导出一种满足虚拟裂纹条件的解析函数,给出物理裂纹尖端扩展的能量释放率Ga、内聚裂纹尖端扩展的能量释放率Gb的计算公式,讨论Ga,Gb,J积分及断裂能GF之间的关系.
1 内聚区内聚力和张开位移函数
1.1 Westergaard应力函数与裂尖奇异解
弹性力学平面问题的求解归结为寻求一个满足双调和方程
∇2∇2φ(z,a)=0
(1)
的解φ(z),并满足弹性体相应的边界条件.对于含裂纹的弹性体,采用复变函数更为便利,其中z=x+iy,a为物理裂纹长度.由此可以求出全部应力分量和位移分量.
对于图1所示的边裂纹平面应力问题,垂直于裂纹面的应力函数为
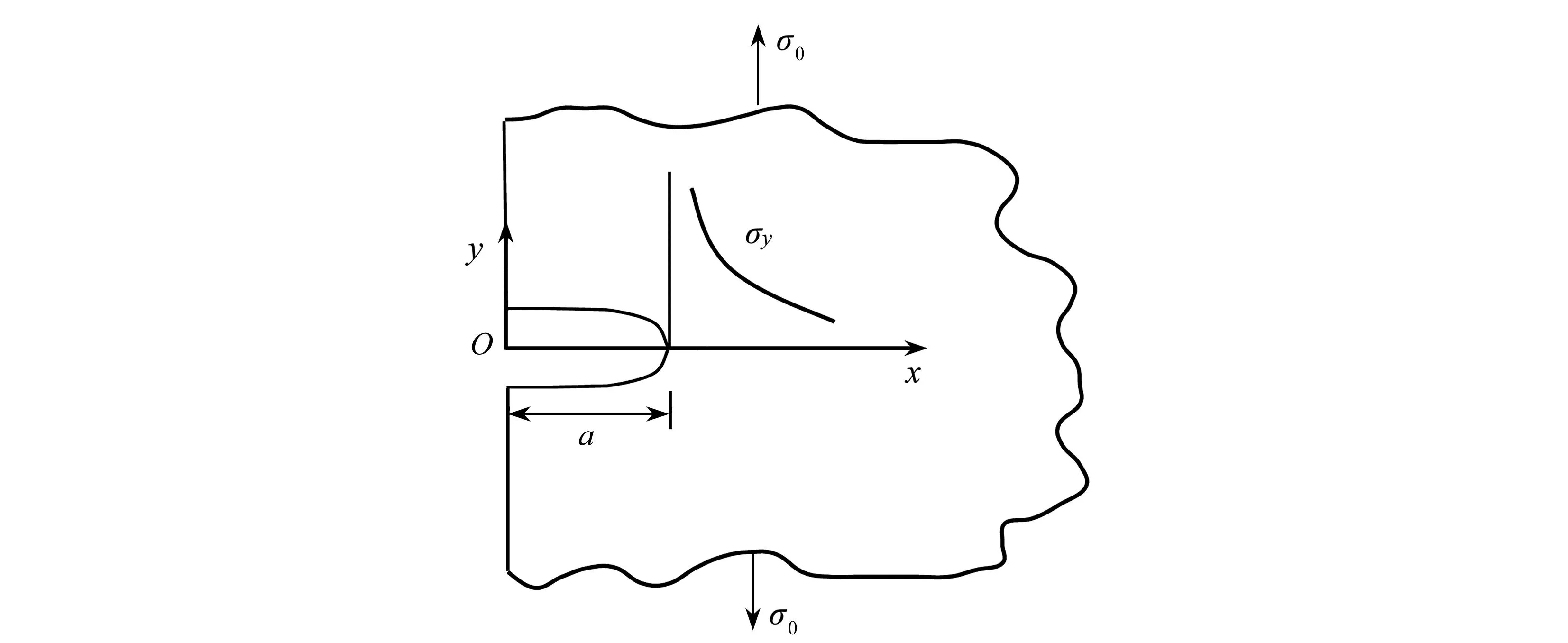
图1 Ⅰ型边裂纹的椭圆张开位移和奇异应力Fig. 1 The elliptic opening displacement and singular stress of a mode-Ⅰ edge crack
(2)
相应的位移函数为
(3)
从式(2)、(3)和图1可以看出,应力在裂尖呈奇异性,其根本原因在于裂尖处的张开位移为椭圆形.
1.2 满足虚拟裂纹条件的非奇异解
参照图2,将带状内聚区模型化为一虚拟裂纹;由文献[15],问题的非奇异解可由对奇异解的加权积分得到,有

图2 内聚区模型的尖劈形张开位移和非奇异应力分布Fig. 2 The wedge opening displacement and nonsingular stress distribution based on the cohesive zone model
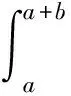
(4)
其中,t替代了a作为积分自变量,b为从裂尖算起沿裂纹扩展方向的长度,ρ(t)为定义在[a,a+b]区间的权函数,其面积标准化为1.为简便起见,令c=a+b,以下的公式仅给出沿x轴的结果.
积分得到的Φ(z,a,b)仍为解析函数,可以作为弹性力学平面问题的应力函数.以权函数为ρ(t)=1/b(a≤t≤c)为例,对式(2)加权积分, 有
得
(5)
对式(3)积分, 得
(6)
从式(4)、(5)和图2可以看出,加权积分解消除了裂纹尖端的奇异性,在区间a≤x≤c,有限应力集中(即内聚力)和光滑尖劈形张开位移相并存,二者关系呈非线性,在物理上可以表征内聚裂纹;但除内聚区外的整个体都是弹性的.
2 内聚区模型的能量释放率Ga和Gb
2.1 内聚区模型的能量释放率Ga和Gb的定义
由上节结果可知,在裂尖延长线上构成了一过渡区间,即把含裂纹界面划分为3个区域(见图2):物理裂纹(真实裂纹)区(x
由Irwin定义的能量释放率G,定义物理裂纹扩展(b一定)的能量释放率Ga和虚拟裂纹扩展(a一定)的能量释放率Gb,分别为
(7)
(8)
其中,B为板的厚度,W(a,b)为裂纹扩展时释放的总势能.
2.2 Ga和Gb的计算
对图2所示的内聚区模型,系统的势能可按下列步骤求得:
1) 首先,考虑在无穷远处作用有垂直于x轴均匀拉应力σ0;同时假设在区间x≤a+b的裂纹表面作用着均匀拉应力σ0,那么这一问题等同于受均匀拉应力作用的无裂纹板.
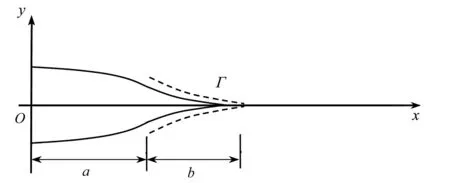
2) 无穷远处的拉应力恒定,物理裂纹区间x (9) 虚拟裂纹区释放的能量为 (10) 3) 所以,从无裂纹均匀受拉状态到形成裂纹a+b的状态,释放的总能量为 W(a,b)=W1(a,b)+W2(a,b). (11) 考虑单位厚度的薄板,Ga和Gb分别为 (12) (13) 由定义,有 (14) (15) 本文模型中,由于消除了裂尖的应力奇异性,若a一定,一旦给定了σ0/σs,b值就唯一确定;由于在裂纹尖端(x=c)处,KⅠ=0,所以有 (16) 则 (17) 或者 (18) 显然,式(18)比式(17)更为便捷. 对于图2所示问题的应力和张开位移解,b一定,物理裂纹尖端t从零扩展到a,将式(6)代入式(14),可得 (19) 同理,a一定,虚拟裂纹尖端t从a扩展到a+b,将式(6)代入式(18),得 (20) 如果虚拟裂纹长度b=0,由上述公式可得 (21) (22) 则式(21)中Ga的结果与基于奇异解的能量释放率G完全一致,具有唯一性;而Gb的值则依赖于虚拟裂纹区的内聚力与张开位移的关系,其值介于(0~1.0)Ga之间,在本文中依赖于假设的权函数. 特别地,虚拟裂纹区的内聚力为恒定值σs时的应力无奇异条件为 (23) 得物理裂纹尖端张开位移为 (24) 此时有 (25) 或者表示为 (26) 由式(26)可得,当b=0时,Gb=0. Rice定义沿路径Γ的J积分为 (27) 其中,ω为应变能密度;Ti为沿路径Γ的作用力矢量;ui为位移矢量;Γ为围绕裂纹尖端的积分线路. 对于本文定义的尖劈形裂纹,取如图3所示的积分路径,此时ω=0,Ti=σy(x,a,b),ui=v(x,a,b),即 图3 J积分线路ΓFig. 3 The J integral path Γ (28) 比较式(17)和(28),因在区间(a,c),对x和对b求偏导等同,可得 Jb=Gb. (29) 对于Dugdale模型,有 Jb=σsδ. (30) 受拉混凝土断裂能GF定义为单位面积内聚裂纹吸收的能量.在虚拟裂纹模型中,被定义为材料拉应变软化曲线下的面积,即 (31) 其中,wc为临界裂尖张开位移,即内聚力σ降为0时虚拟裂纹的最大宽度,而在虚拟裂尖处的内聚力达到材料极限强度σs,此处的w对应于本文模型的2v,wL与虚拟裂纹临界长度bc一一对应.因此,GF在数值上等于临界能量释放率Gc或临界J积分值Jc,即 GF=Gbc=Jbc. (32) 文献[20]的解析模型揭示了虚拟裂纹面上某点处的内聚力σy与该点的张开位移v之间的关系,这一关系正是材料拉应变软化曲线,软化曲线包围的面积正是断裂能GF,即每单位面积裂缝面完全断开所吸收的能量. 本文的解析对象为一半无限大板,且除了内聚区外,材料处于线弹性状态,因此: 1) 随着试件尺寸的增大,整体的线弹性条件逐渐得到满足,测得的Gac和Gbc也趋于真实值. 2) 只有当b/a趋于零(相当于完全线弹性或小范围屈服),即内聚区不存在或很小时,才可以测得真实的Gac值(相当于线弹性断裂韧度GIC),此时Gbc将失去意义. 3)Gb随着b的增加而增大,当b达到一临界值bc时,内聚区完全形成,其物理裂尖的内聚力降为零,Gbc=GF,裂纹开始失稳扩展,所以Gbc可以作为含内聚区材料的断裂韧性. 4) 对于类似于混凝土的拉应变软化材料,裂纹失稳扩展后,试件的承载力会逐渐下降,内聚区不断前移,可以由Gac来评估试件的剩余强度. 5) 但在实验测试中,断裂能GF的尺寸效应还来源于内聚区以外的附加耗能.采用一般测试手段,要测得真实的断裂能,除了试件尺寸要求外,还对加载试验机提出了很高的刚度要求.如采用三点弯曲试件由实测P-δ曲线计算断裂能时,就包含了内聚区以外的能耗,因而高估了GF值.试件尺寸越大,内聚区以外的塑形能也越多[21],使得小试件情况下,GF>Gbc;只有当试件足够大,且扣除了内聚区以外的附加耗能时,才有GF=Gbc[22]. 6) 文献[23-24]的研究表明:试件尺寸、初始裂缝相对尺度对测试断裂能产生显著影响.本文的理论模型具有普遍意义,有限边界试件的内聚区模型解可结合边界配置法得到近似解[25],并由此导出Gb,Jb等的计算值;随着物理裂纹的扩展,有效韧带的尺度逐渐减小,边界条件的变化使得能量释放率G或J积分值的精度会越来越差,由此可以对材料断裂参数的尺寸效应进行评估.如果采用通过测试内聚区张开位移获得拉应变软化曲线的方法,所得的断裂能将不受内聚区以外附加耗能的影响[26]. 基于导出的满足内聚裂纹条件的解析解,讨论了物理裂纹尖端扩展的能量释放率Ga、内聚裂纹尖端扩展的能量释放率Gb的计算,以及Gb与J积分之间的关系,推导出了Gb更为简洁的计算公式(18),并证明了Gb=Jb.只要试件足够大,临界能量释放率Gbc(或临界积分Jbc)就是断裂能GF,表明Gbc可以作为含内聚区材料的断裂韧性来判别裂纹的失稳扩展.但试件的实测GF值总是大于Gbc(Jbc)值,主要是源于内聚区以外的附加耗能的影响. 本文提出的方法适用于所有含Ⅰ、Ⅱ、Ⅲ型内聚裂纹的弹性体,对于断裂力学内聚区模型的研究和应用具有重要参考价值.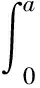
2.3 Dugdale模型的Gb
3 Ga,Gb与J积分、GF的关系
3.1 J积分与Gb的关系
3.2 Gb与GF的关系
3.3 讨论
4 结 论
