数据驱动下的声学器件音质优化*
2024-04-10张维声
许 磊, 张维声, 朱 宝, 郭 旭
(大连理工大学 工程力学系, 辽宁 大连 116024)
0 引 言
近几十年来,结构设备和电子器件的声学性能逐渐成为工程设计中的一个研究热点.随着声学器件的性能需求的提升,相关设计问题也不断面临新的挑战.
为了满足声学设计要求,拓扑优化[1-3]已被广泛地应用于声学优化设计中.2007年,Yoon等[4]提出了一种混合有限元公式,并结合变密度法(SIMP)有效地解决了材料在结构域与声学域之间的平稳过渡,实现了参考域内的声压水平最小化设计.Du等[5]考虑了结构与周围声学介质间发生耦合作用,通过对无阻尼振动双材料弹性结构进行拓扑设计,实现了结构振动传递到声介质的声能最小化.Lee等[6]采用正态导数积分方程求解了薄体结构的声学问题,并使用遗传算法对薄体结构的孔洞设计进行了拓扑优化.Hu等[7]提出了一种基于混合有限元公式和替代材料模型的浮动投影拓扑优化方法,能够有效地降低声学优化问题中由极高的质量和刚度比引起的人工局部振动模式.
尽管现阶段在声学拓扑优化设计方面已开展了诸多研究,但大多关注的是单一频率下的声压/声能最小化设计[8-10],而对频带内音质的提升关注较少.在电子声学器件中,音质指的是在某一频带内,声音能够以一定的幅值强度平稳输出.音质优化一般将关注频带离散成一定数量的频点,并对所有频点的声学响应进行协同优化.事实上,当频带内离散的频点数量足够多时,声频响曲线的表现精度会更高.然而伴随着高精度的声曲线输出,大规模频点响应的反复优化使得问题的可求解性大幅降低.
针对上述问题,本文提出了一种基于人工神经网络的声-结构耦合系统的显式拓扑优化框架.在该框架下,采用MMC[11]显式描述结构域与声学域的边界,并以人工神经网络模型代替求解耗时的有限元计算模型对声-结构系统的声频响进行预测,从而实现音质优化问题的快速求解.
1 声-结构系统优化模型
在本文中,音质优化的目标是通过改变设计域的拓扑结构来找到最优的声学结构(如图1所示),从而提高某一频带内声压频响的幅值,改善频带内声频响的均匀性.引入2014年由Guo等[11]提出的MMC法,以声学指标I最小化为目标函数,优化列式可以表述为
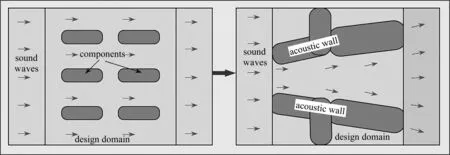
图1 声学优化问题示意图Fig. 1 Schematic diagram of the acoustic optimization problem
(1)
其中,di(i=1,2,…,N)为第i个组件的设计变量向量,N为组件总数;Ud为d的可行集;I为由声压表示的目标函数;K为总体刚度矩阵;F为全局载荷向量;U为包括机械场和声场的结构响应;Da为给定的设计域;γ为在0和1之间的体积分数.
式(1)中,忽略体积力,声-结构耦合系统控制方程KU=F的离散形式为
(2)
其中,ω=2πf为角频率;ρa为声学材料密度;Kuu和Muu分别为结构刚度矩阵和结构质量矩阵;Kpp和Mpp分别为声学刚度矩阵和声学质量矩阵;Kup为耦合矩阵;u和p分别为结构位移向量和声压向量;fu和fp分别为结构载荷向量和声力向量.式(2)的详细推导过程和公式表达可参见文献[12-13].
对于声压级最大化问题,目标函数可以表示为
I1=-‖pi‖2, ∀i∈[fl,fu],
(3)
其中,pi表示频带[fl,fu]内频点i的声压频响.而对于音质优化,需要对声压幅值和均匀性同时进行优化,目标函数可以表示为
(4)
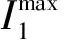
(5)
其中,Nf是离散频率点的总数,p是一个惩罚因子,在本文中,p=6.
2 方 法 介 绍
2.1 MMC方法介绍
在MMC拓扑优化框架中,结构构型可以由一系列组件通过移动、变形、旋转等行为搭建而成,这些组件可以由拓扑描述函数显式表达.在本文中,一个2维结构组件的拓扑描述函数[14]可以表示如下:
(6)
其中
(7)
(8)
在这里,向量d=(x0,y0,L,t1,t2,t3,θ)表示组件的设计变量.其中,(x0,y0)表示组件中心点的坐标,L表示组件的半长,t1,t2,t3分别为组件两端和中间的半宽,θ表示坐标系x′O′y′相对于坐标系xOy的倾斜角,m为一个较大的偶数,在本文中,m=6.向量d所描述的组件如图2所示.
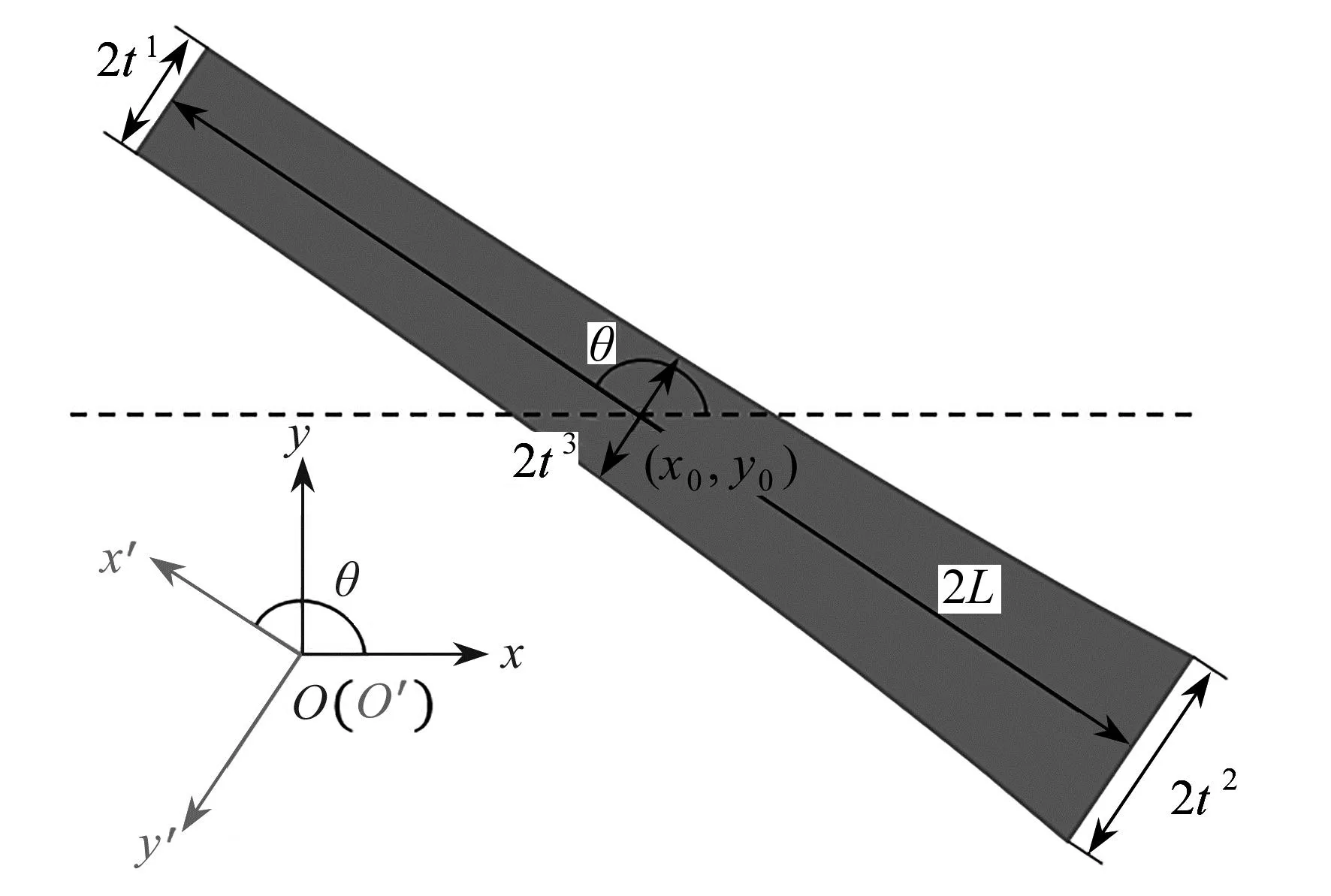
图2 一个二维结构组件Fig. 2 A 2D structural component
对于每个组件,第i个组件占据材料域Ωi和边界∂Ωi的拓扑描述函数如下:
(9)
其中,x为设计域Da中的任意一点并且Ωi⊂Da,φi(i=1,2,…,N)为第i个组件的拓扑描述函数.由此,设计域内所有结构组件的拓扑描述函数可以写为
(10)
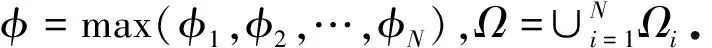
2.2 灵敏度计算
为了求解优化公式,采用伴随法求出目标函数/约束函数对设计变量的灵敏度.式(4)中音质问题的目标函数I2关于设计变量x的导数为
(11)
其中
(12)
(13)
在本文中,由于目标函数I是由神经网络模型预测获得的,因此可以直接通过有限差分法来计算目标函数I对设计变量x的导数,这对复杂问题的灵敏度计算十分有效.
2.3 BP神经网络模型原理
近些年来,数据驱动方法得到了快速发展,并在力学领域的求解计算方面开展了诸多应用[15-17].本文通过构建基于BP神经网络的声-结构耦合系统频响预估模型,可以快速准确地预测声频响.典型的BP神经网络分为3个层次:输入层、隐藏层、输出层.每一层包含一组神经元,神经元和连接它们的各种权重组成了神经网络.通过输入一定数量的数据集,并对其进行训练,神经网络可以快速准确地预测一系列输入所对应的输出.
在本文中,以结构组件的几何参数和激励频率作为输入变量,以声压频响作为输出变量,构建用于预测声-结构耦合模型声频响的BP神经网络模型.BP神经网络模型详细的构建过程如下:
1) 采集数据.使用Latin超立方采样(Latin hypercube sampling,LHS)均匀产生组件几何参数d和激励频率f,并与仿真计算得到的目标函数I一起作为数据样本.
2) 预处理数据.为了避免奇异样本的出现,对原始数据进行归一化处理,使得数据映射在[-1,1]之间.
3) 建立BP神经网络.BP神经网络包含1个输入层、10个隐藏层、1个输入层.输入层包含15个神经元,每个隐藏层包含200个神经元,输出层包含1个神经元.
4) 设置训练参数、测试性能及计算误差.设置包括学习率、一次性选取样本数、训练周期等相关参数.对建立的模型性能进行检测,通过计算均相对误差(mean relative error,MRE)对模型的预测结果进行评估.
图3为使用BP神经网络模型进行音质优化的流程图.
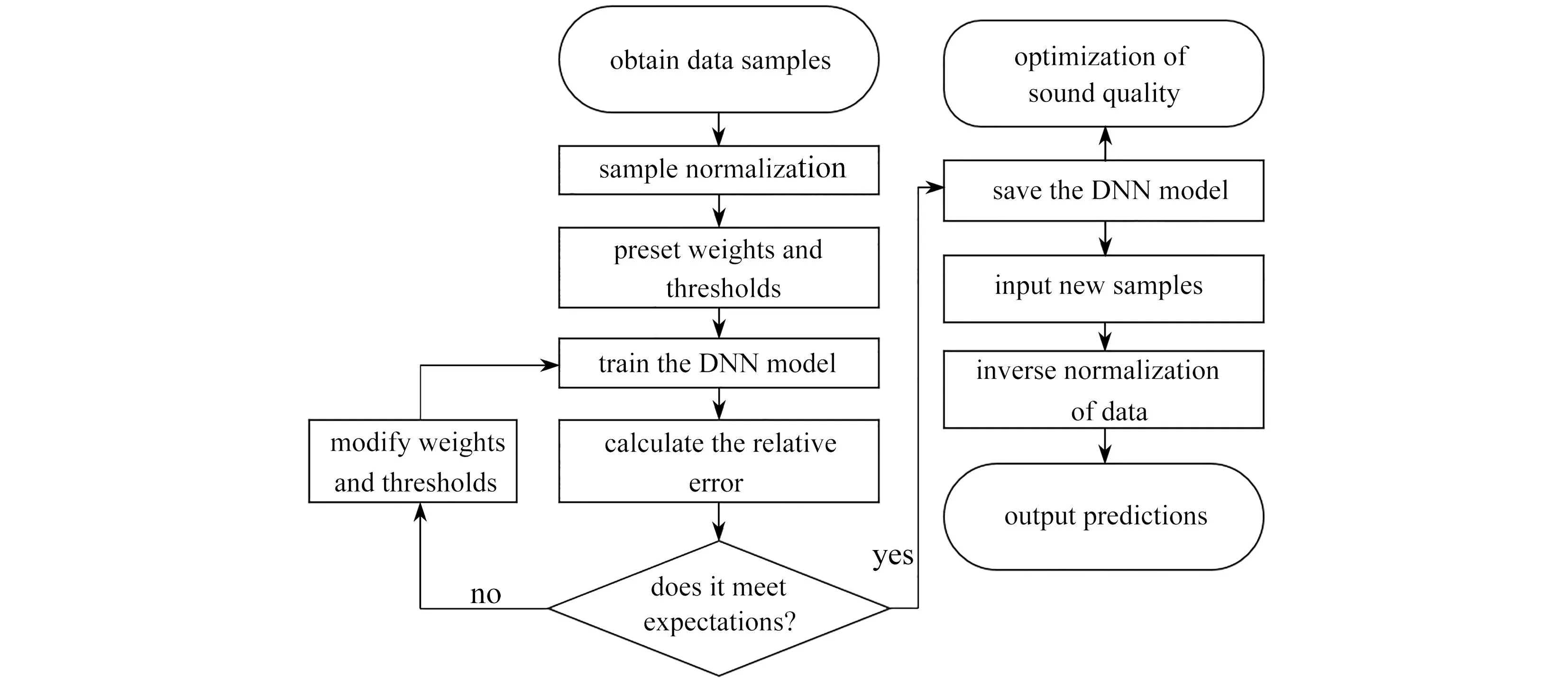
图3 利用BP神经网络进行音质优化流程Fig. 3 The flow chart for the sound quality optimization with the BP neural network
3 数 值 算 例
3.1 有限元模型
如图4所示:声-结构耦合模型左侧为结构域, 材料为塑料, 尺寸为0.2×10, 上下为固定边界, 载荷F=1 N;右侧为声学域并充满空气,尺寸为20×10,上下为声场硬边界,右边界为声场辐射边界,左边界为声-结构耦合边界.声学设计域尺寸为2.5×10,与耦合边界相距5,点A为声辐射边界中点.在本文中,为了解决声压级最大化和音质优化两个不同的问题,模型的尺寸单位分别采用mm和cm.整个结构离散化采用202×100的均匀网格.
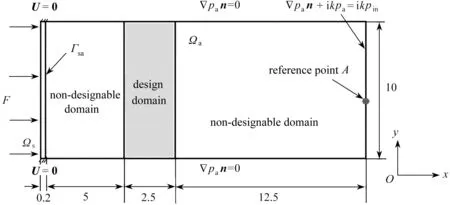
图4 一个简化的二维声-结构耦合模型Fig. 4 A simple 2D acoustic-structural coupled model
我们为了简化计算,随机产生14个几何参数生成2条结构组件,然后通过对称操作在设计域上方生成2个镜像组件,组件的内部材料为铝.材料属性如表1所示.

表1 3种材料的参数
针对声压级最大化和音质优化两个问题,24万组单频(频率为7 000 Hz)声学响应数据样本和18万组多频(频带范围为3 000~4 000 Hz)声学响应数据样本分别被收集并用于训练BP神经网络,计算所得MRE均在1%以下.
3.2 声压级最大化问题
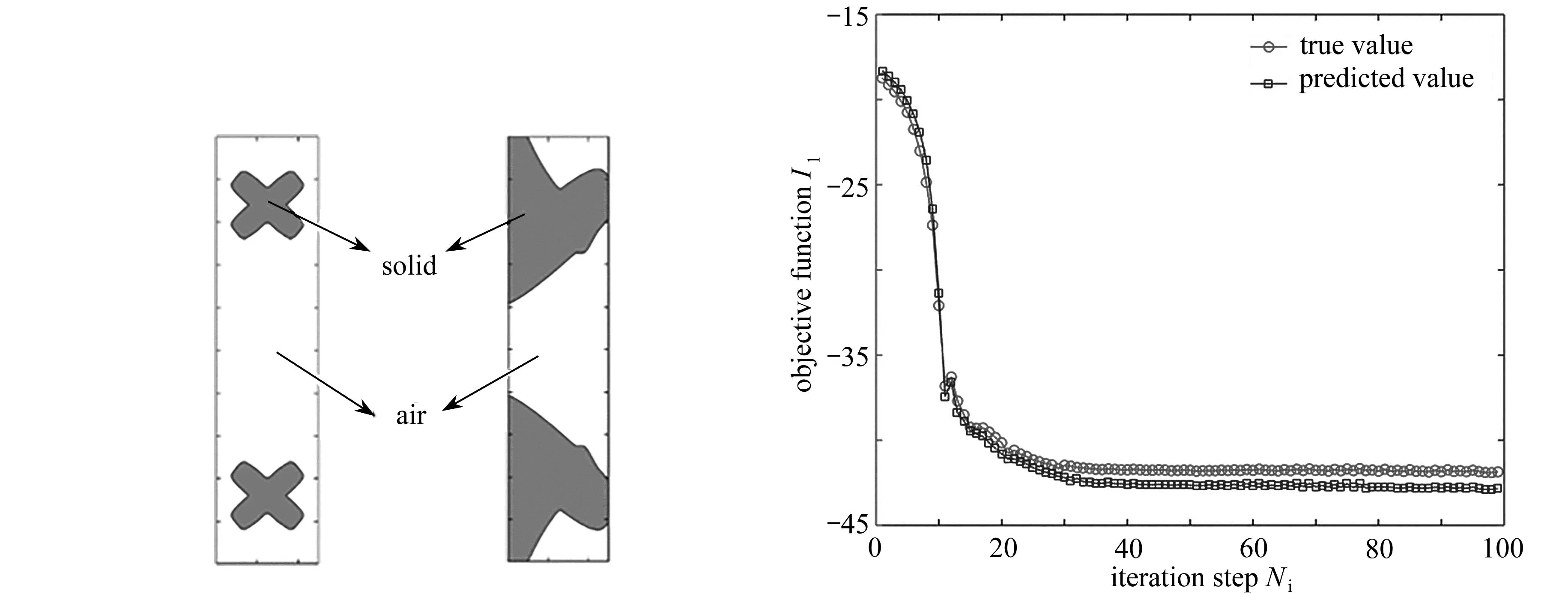
图5 组件初始布置和最终优化设计
图7显示了纯空气设计与最优设计的声压级场分布.图8为纯空气设计与最优设计的声压级曲线,可以发现7 000 Hz下点A处的声压级由102.89 dB提升至107.43 dB,优化效果显著.

(a) 纯空气设计 (b) 最优设计(a) The pure air design (b) The optimized design

图8 纯空气设计和最优设计的声压级曲线([6 000 Hz, 10 000 Hz])Fig. 8 SPL curves of pure air design and the optimized design ([6 000 Hz, 10 000 Hz])
3.3 音质优化问题
接下来是音质优化.在3 300~3 700 Hz频带范围内均匀选取41个频点,目标函数为I2,系数η=0.01.图9显示了最终优化构型,可以发现组件在设计域内形成了3个声通道,中间的声通道成左宽右窄状,上下两端各有一个不规则的狭窄声通道.其中,上下两端的声通道有利于声波向目标点A处聚集,能够在一定程度上提升声压级值;而中间的声通道形状比较复杂,对声波起到一定的反射和抑制作用,这一复杂的声腔结构能够有效地提高目标频带内声压级值的均匀性,有利于改善音质.图10为目标函数和体积约束的历史迭代过程,可以发现目标函数快速下降并在第46步后收敛.对最优构型进行有限元扫频计算,图11为纯空气设计和最优设计的声压级曲线,可以发现在3 300~3 700 Hz频带内,纯空气结构的声压级曲线出现了明显的波峰与波谷,声压级大小在32.99 dB至77.88 dB范围内(差值为44.89 dB).而最优结构的声压级在68.93 dB至75.42 dB范围内(差值为6.49 dB),声压级频响曲线更加平稳,音质得到了显著提升.另外,本算例中,200迭代步只花费了446 s,相比完全基于有限元与解析敏度的优化计算(41个频点,200迭代步花费7 300 s),求解速度约为之前的16.3倍.对于三维声学器件模型,使用上述优化方法同样可以快速得到最优拓扑构型,并能够有效改善音质.三维算例的具体流程与二维情况相同,这里不再赘述.
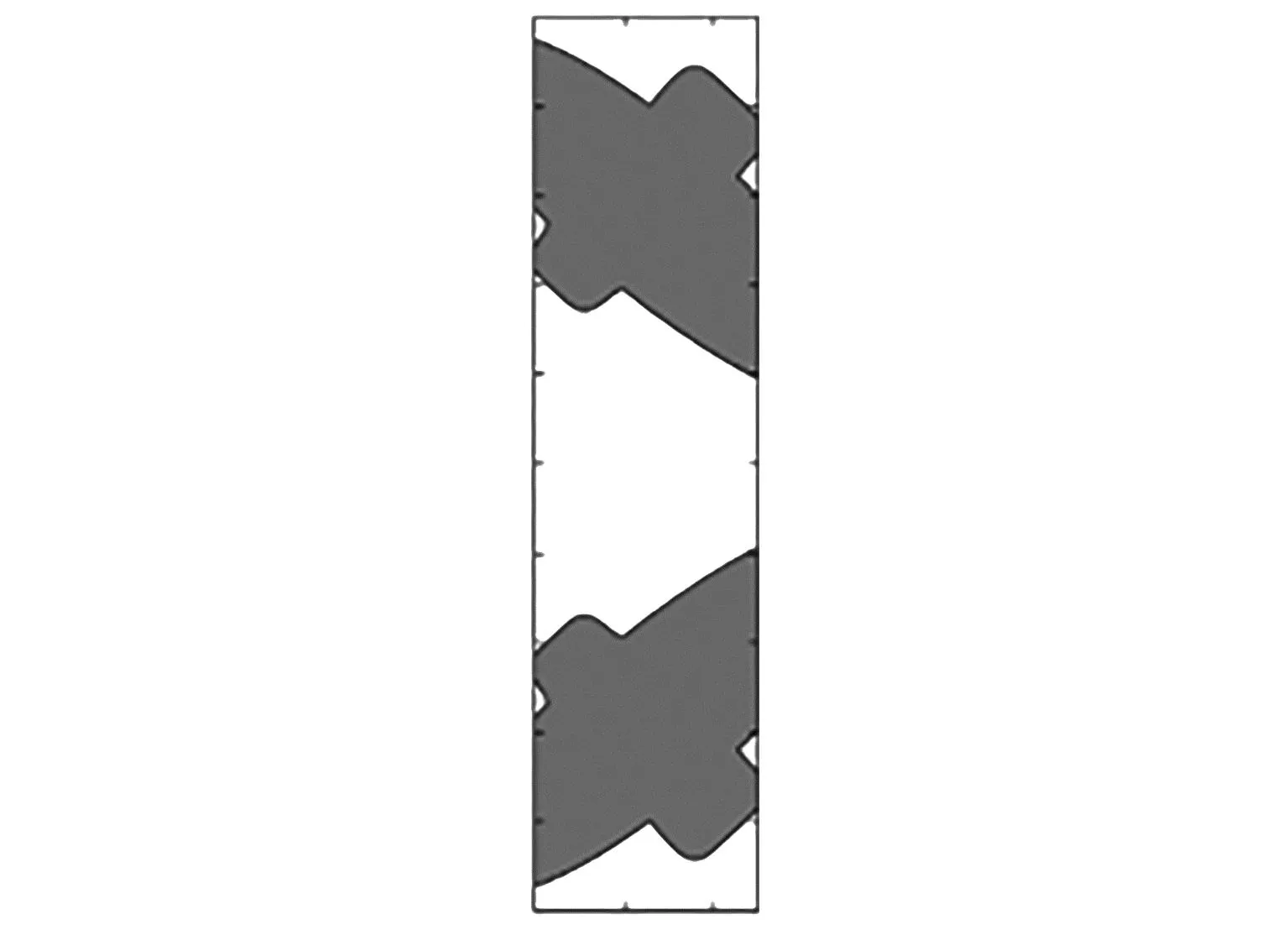
图9 最终优化构型Fig. 9 The final optimized design
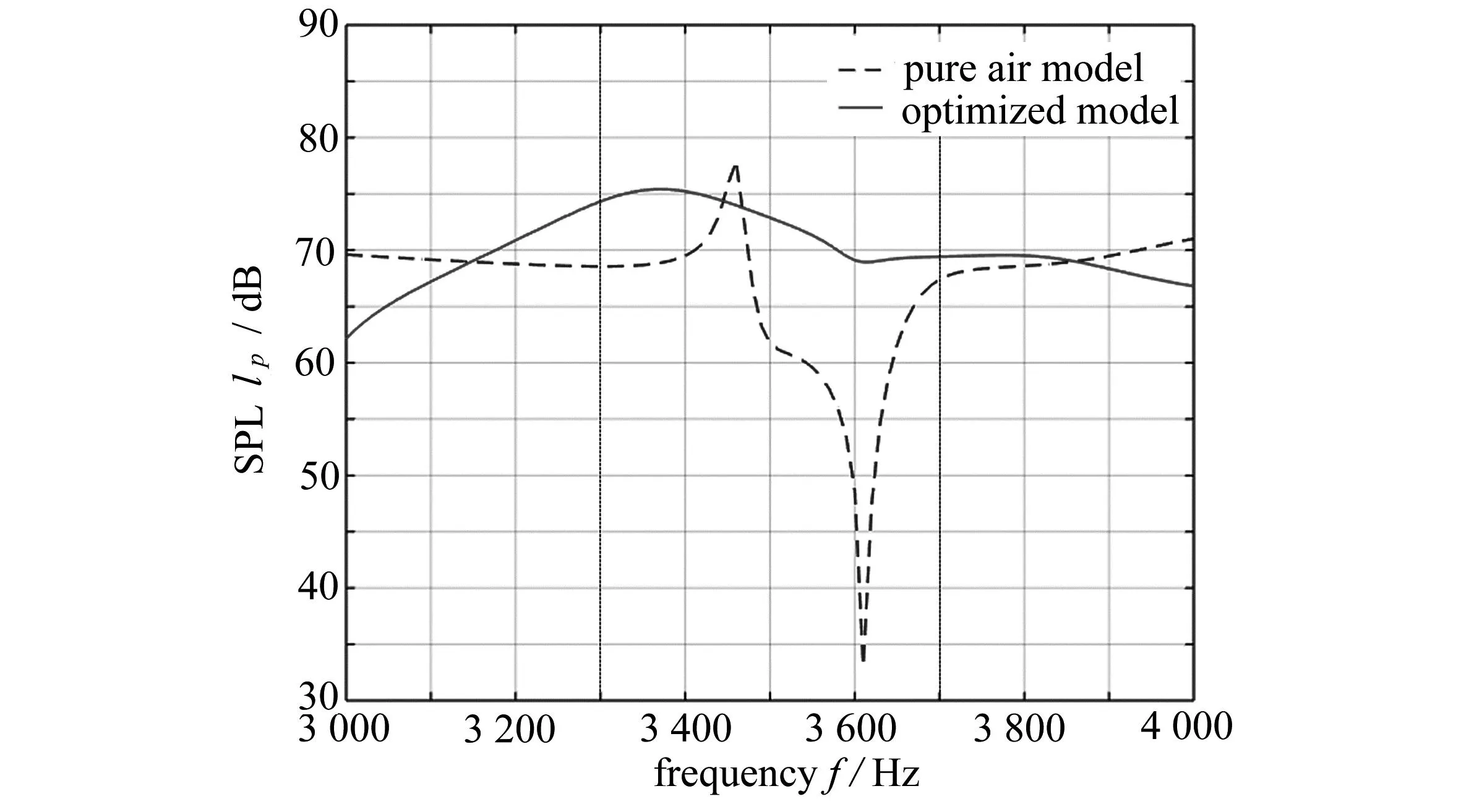
图11 纯空气设计和最优设计的声压级曲线([3 000 Hz, 4 000 Hz])Fig. 11 SPL curves of the pure air design and the optimized design ([3 000 Hz, 4 000 Hz])
4 结 论
本文针对音质优化问题,利用人工神经网络建立了声-结构系统的声频响预测模型,解决了由于结构设计参数、激励频率与声频响之间的非线性关系造成理论建模困难的问题.结合MMC显式拓扑优化方法的少量几何参数,极大地降低了神经网络模型的输入维度.利用LHS得到均匀分布的几何设计变量和激励频率,与有限元计算的声频响作为数据样本,通过训练得到了神经网络模型.数值算例验证了神经网络预测结构声频响的准确性,预测值和优化过程的真实值之间的吻合性很好.利用训练好的神经网络对声学结构进行音质优化,所得最优结构可以有效地将目标频带内的声压级范围差从44.89 dB缩小至6.49 dB,声学器件音质改善明显.另外,在该方法下,目标函数可以快速收敛,相较于基于有限元与解析灵敏度的优化计算,求解速度约为之前的16.3倍,计算效率得到了大幅提升.
