弹性膜对部分充液罐车内液体晃动的抑制效果研究*
2024-04-10祁文超王琼瑶陈馨儿
祁文超, 王琼瑶, 平 凯, 陈馨儿
(五邑大学 智能制造学部, 广东 江门 529020)
0 引 言
液体和储罐结构之间的相互作用可能导致结构失效或损坏.由于负载总质量的限制,储罐通常处于部分填充状态[1].在制动操作过程中,液体运动将导致液体货物的载荷转移,从而产生晃荡力和力矩,导致车辆侧倾稳定性和制动性能下降[2].报告的事故数据表明,由于液体晃动引起的动态晃动力和力矩,液体罐车会比其他货运车辆更频繁地发生事故[3-5].
早期的研究集中在隔间或刚性壁[6-7].然而,隔间或刚性壁除了大大增加系统的重量外,还对清洁和维护工作造成障碍.在随后的研究中,挡板作为一种更优化的结构被研究人员广泛研究和采用[8-11].Goudarzi等[12]的研究表明,挡板的抑制效果受储罐纵横比的影响.Kolaei等[13]使用边界元方法研究了具有不同长度的底部安装、顶部安装和中心安装部分挡板的储罐.结果表明,底部安装的挡板仅在非常低的填充率下有效,而顶部安装的挡板在高填充率下更有效.除了在固定式储罐中的应用外,挡板也广泛用于移动式储罐[14].Wang等[15]研究了几何参数(如挡板曲率、开口尺寸和形状以及倾斜度)对晃荡力和载荷传递的影响,并注意到挡板之间的气压对抑制液体晃荡的贡献.Ünal等[16]评估了T型挡板的抑制晃动性能.结果表明,当T形挡板的高度超过液位的80%时,可以得到很好的抑制效果.Korkmaz等[17]发现,穿孔挡板会消耗储罐中液体晃动的动能,这将降低侧壁上的压强,并改变储罐的固有频率.Thirunavukkarasu等[18]发现,当挡板放置在自由表面附近时,挡板在抑制液体晃动方面非常有效,并且在不同情况下给出了挡板结构的最优形式.
尽管刚性挡板对液体晃动有明显的抑制效果,但刚性挡板大大增加了系统的质量,并且在应用中有许多限制.因此,一些研究人员提出用弹性挡板代替传统的刚性挡板,并通过实验或仿真证明弹性挡板大大减轻了系统的重量,并获得了相对较好的抑制晃动效果.Hwang等[19]通过比较无挡板、刚性挡板和一组弹性挡板的数值结果发现,弹性挡板在抑制晃动效果方面与刚性挡板相当,但弹性挡板更轻,因此单位质量更有效.Zhang等[20]通过基于光滑有限元法(SFEM)和改进的光滑粒子流体动力学(SPH)的耦合策略,对带有弹性挡板的储罐中的晃动现象进行了数值研究.结果表明,弹性挡板的几何方位和参数特性对罐壁冲击压强有显著影响.
此外,一些研究人员认为弹性膜对液体晃动也有抑制作用[21-22].Chiba等[23]研究了在垂直激励下,覆盖弹性膜的球形储罐中的液体晃动特性.结果表明,覆盖自由表面的弹性膜显著抑制了自由表面的大振幅非线性响应.Wang等[24]研究了液体与弹性膜的相互作用,并在纵向或横向谐波加速度激励下,在带有弹性膜的按比例缩小的储罐上进行了一系列实验,还对弹性膜的抑制晃动效果进行了仿真分析.结果表明, 膜的加入可以大大降低晃动幅度, 从而降低俯仰力矩, 并且晃动频率可以增加到更高的值, 以避免部分填充储罐中的共振.
本文提出了一种覆盖液体自由表面的多段弹性膜.考虑了空气、液体和弹性膜在封闭罐中的相互作用.对部分填充的矩形储罐进行了流体-弹性膜相互作用的双向流固耦合(FSI)模拟.进行了实验室实验,证明了模型的有效性.通过比较不同弹性膜配置的储罐获得的储罐晃动响应,验证了弹性膜的有效性.
1 流固耦合模型
1.1 基本参数
模拟是在一个长10 m、高2.4 m的二维矩形储罐中进行的.填充比设置为0.5,液体自由表面被几段弹性膜覆盖,弹性膜的厚度为0.01 m,每个膜的边缘保持固定,如图1所示.为了便于描述,将4种罐配置分别命名为T0、T1、T2和T3.Wang等[24]获得的研究结果表明,如果液体被膜完全覆盖,施加在罐壁上的液体压强将比T0罐更大.因此,在本研究中,液体自由表面被几段膜覆盖,如图1所示.即每个弹性膜之间有一个间隙.

(a) 无膜储罐 (b) 装有两段弹性膜的储罐(a) The tank without membrane (b) The tank with 2 elastic membranes
对于T1、T2和T3储罐,间隙的总间距保持恒定为0.5 m,因此单段弹性膜的尺寸分别为4.75 m,3.17 m和2.375 m; 液体和空气的密度分别为1×103kg/m3,1 kg/m3; 弹性膜的弹性模量为2×108Pa,Poisson比为0.38,密度为9.6×102kg/m3.考虑到弹性膜的大变形,数值模型中采用超弹模型对弹性膜进行建模.
1.2 流体域控制方程
在开源软件OpenFOAM中对部分填充液罐车内的液体和气体进行建模.液体和气体的运动可以通过连续性方程和动量方程描述:
(1)
(2)
u为速度矢量,p为流体压强,ρ为流体密度,μ为流体黏度;ai表示由于重力或液罐车操纵引起的加速度激励的加速度分量.
流体体积法(VOF)用于跟踪液相和气相之间的界面[25].VOF方法引入了标量α来表示液相在给定网格中占据的体积.因此,当α=1时,意味着网格完全被液相占据;当α=0时,意味着网格完全被气体填充;当0<α<1时,表示网格在气液界面上由部分气体和部分液体组成.
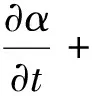
(3)
式中,第三项为人工添加的可压缩项,在纯相中为0,仅在0≤α≤1处存在值;c表示可控的压缩因子,c=0时无压缩效果,c越大,压缩效应越明显.某一单元中的局部密度(ρ)和黏度(μ)由相应的α决定[26]:
ρ=αρfluid+(1-α)ρair,
(4)
μ=αμfluid+(1-α)μair.
(5)
考虑到实际运输容器为密闭容器,因此将储罐壁建模为刚性壁面,应用无滑移边界条件.这意味着流体在壁面的速度(ufluid)等于壁面的速度(uwall):
ufluid=uwall,
(6)
对于壁面边界条件,除了将边界法向通量设置为零以外,同时也需要考虑剪切应力:
(7)
式中,u∥为平行于壁面的速度,d⊥为从边界单元形心到壁面的法向距离.
1.3 固体域控制方程
在开源软件deal.Ⅱ中对弹性膜进行建模.弹性膜的控制方程可以表示为[27]
(8)

(9)
式中,L0和Ls分别为弹性膜变形前后的长度,c为弹性膜的跨度.
将弹性膜均分为M个单元,使用Hermite多项式逼近变量y,方程(7)的空间离散形式使用Galerkin加权余量法获得[28]:
(10)
式中
(11)
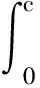
(12)
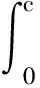
(13)
(14)
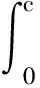
(15)
方程(10)—(14)组成了非线性常微分方程组,使用广义α(generalizedαmethod)方法进行求解.
本文使用Gauss-Seidel迭代法逐步逼近解来得到最终的解.在每次迭代过程中,Gauss-Seidel方法会更新未知变量的值,直到达到预设的精度要求或最大迭代次数.对于一个给定的线性方程组:
Ax=b,
(16)
Gauss-Seidel方法可以表示为
(17)
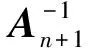
1.4 流固耦合
PreCICE是一个基于C++的开源多物理场耦合环境库,使用任意Lagrange-Euler方法(ALE)的方式实现分区模拟,并使用现有求解器的API实现数据交互.对于流体子问题,使用Euler方法描述流体的运动;对于固体子问题,使用Lagrange方法描述固体的运动和变形.PreCICE通过交换力和位移数据实现流体域和固体域之间的数据交换和耦合[29].耦合面控制条件可以表示为
Ff·nf=Fs·ns,
(18)
xf=xs,
(19)
式中,Ff和Fs分别表示耦合面上的流体作用力和作用域固体的作用力,nf和ns分别表示流体域和固体域耦合面的法向向量,xf和xs分别表示流体域耦合边界和固体域耦合边界的位移.

(20)
式(20)被称为定点方程(fixed-point equation).本文采用IQN-LS方法来稳定和加速耦合迭代,通过利用前一步迭代的输入和输出数据来近似计算固定点公式残差算子的逆Jacobi矩阵,并执行类似于Newton法的求解步骤.同时,为避免潜在的奇异性问题,采用基于QR的滤波技术来过滤掉线性相关的数据,以确保计算的稳定性和准确性.
式(20)可以改写为如下形式:
sn+1=S(F(sn+1))=S∘F(sn+1),
(21)
其广义形式为
x=H(x),
(22)
式中,H表示S∘F,所以迭代松弛法可以将式(21)改写为
xi+1=H(xi)+(ωi-1)(H(xi)-xi),
(23)
式中,ωi为第i次迭代的松弛系数.
该松弛过程收敛的判断条件为
(24)
(25)
式中,ξ为预先设定的收敛限,‖·‖2为矩阵的二范数.
本文采用径向基函数映射算法(RBF)处理耦合面网格单元拓扑信息不匹配的问题.在位移变换过程中采用了一致映射,而对于力映射则采用了保守方式,这使得两侧的数据值之和相等,从而确保了界面处的能量平衡.
1.5 晃动响应分析
模拟是在纵向加速度激励下进行的,这是理想化的刹车激励.加速度激励可以用斜坡阶跃的方式表示:
(26)
式中,a(t)为加速度函数,k为加速度上升率,β取0.2,是用于分层斜坡阶跃函数不连续性的弧函数的参数,ε是加速度的稳态值,取为0.3g,如图2所示.从图中可以看出,加速度的值在达到最大值后保持不变,这与实际的刹车加速度激励有所不同,采用这种设定主要是为了分析弹性膜在液体晃动达到稳态时对其的影响.

图2 斜坡阶跃加速度激励Fig. 2 The rounded ramp-step acceleration input
载荷转移量是判断液体晃动剧烈程度的重要指标.通过液相的质量中心(cg)的瞬时坐标相对于坐标原点的变化来评估:
(27)
(28)
式中,V是液体总体积,xc和yc是单元c的中心坐标,φ定义积分域,如图3所示.图3中纵向定义为X方向,而垂向则表示为Y方向.

图3 质心坐标以及晃动力和俯仰力矩的计算Fig. 3 Calculation of centroid coordinates, slosh forces and pitch moment
晃动力由储罐内壁和弹性膜的边界单元的压强积分获得
(29)
式中,Fi是沿着轴线i(i=x,y)的合成晃荡力,Aei是沿着轴线i投影的单元e的面积.
力矩是通过每个单元力和单元相对原点的位置矢量的叉积的积分获得,因此
(30)
式中,le是单元相对于坐标原点的位置矢量,Fe是施加在单元格e上的力.
2 实验和模型验证
2.1 实验设计
为了验证数值模型的准确性,我们进行了一系列晃动实验.实验是在尺寸为0.3 m长、0.2 m高的矩形储罐中进行的,电动机的转速使用可编程电机控制器控制,如图4所示.

(a) 控制部分 (b) 移动平台(a) The control module (b) The movement platform
该储罐由丙烯酸制成用于可视化并安装在移动平台上.为了消除液体晃动的三维效应,储罐的宽度设置为0.04 m.罐壁的厚度设置为8 mm以避免罐壁的振动.将分辨率为0.000 5g、采样间隔为0.1 s的加速度传感器安装在储罐上以记录加速度的时间历程.传感器使用蓝牙与个人电脑进行数据传输.容器内水的深度为35 mm,并加入蓝色染料以提高能见度.使用分辨率为每秒60帧的相机来捕捉实验的快照以与模拟结果进行比较.
2.2 两相流模型验证
加速度传感器记录的储罐运动加速度的时间历程如图5所示.在运动的初始阶段,可以看到-4.55 m/s2的加速度值,这是由于电机突然接收到运动命令后速度突变引起的.在随后的往复运动过程中,加速度的时间历程体现了类似正弦波的特征,并且当移动平台运动到极限位置时,加速度在一定程度上波动.
数值模拟是在与实验相同的条件下进行的.通过实验和模拟获得的自由表面变形的比较如图6所示,左图为实验快照,右图为数值模拟.选择0.4 s至7.3 s之间的8个时刻进行比较.从图中可以看出,数值模型获得的自由表面变形与实验结果吻合得很好,这表明了本文数值模型的有效性.然而,在3.2 s,4.4 s和5.5 s,实验中可以看到自由表面附近的一些空气夹带,而在模拟结果中没有看到这种现象.数值结果与相应实验结果之间的微小差异可能归因于本研究中采用的层流模型,显然,湍流模型更适合捕捉液体晃动的微小特征.由于在本研究中主要关注液体的整体运动,因此选择层流模型是可以接受的.
2.3 流固耦合模型验证
Liao等[30]进行了溃坝冲击弹性板的实验,弹性板固定在水箱下端,距离右侧0.2 m,水柱靠近水箱左侧,如图7(a)所示.水柱通过闸门保持静止.当闸门移除时,在重力的作用下水柱会向下倾泻并冲击弹性板.在液体的冲击下,弹性板会发生严重变形,这使其成为评估本文提出的流固耦合数值模型稳健性的良好基准.

(a) 模型设置 (b) 弹性板顶端位移时程(a) The initial problem setup (b) The plate tip horizontal displacement time history
图7(b)显示了在弹性板尖端测量的水平位移的时间历程.目前的数值结果与Liao等[30]的结果较为一致.值得注意的是,在t=0.4 s以后,数值结果和实验结果之间会出现一些差异.这些差异可能归因于数值模型中采用的超弹模型.
3 结果和讨论
根据晃动力和力矩、液体载荷转移、施加在罐壁上的压强等方面的晃动响应,评估了各种膜结构抑制晃动的效果.
3.1 网格无关性检验
在本研究中使用了结构网格.考虑了1.8 cm,1.6 cm,1.4 cm三种网格尺寸进行网格无关性检验.在斜坡阶跃加速度下对具有50%填充率的T0储罐进行了测试.此外,通过将Courant数限制在0.5以下的条件自动调整时间步长.由于T0储罐中的液体晃动更剧烈,如果在这种情况下通过网格无关性验证,则足以满足其他储罐配置的要求.图8显示了三种网格尺寸获得的俯仰力矩的时间历程.结果表明,用1.4 cm和1.6 cm网格获得的结果较为一致,但用1.8 cm网格得到的结果在2 s后产生一些偏差.原因是储罐中的液体冲击罐顶,经历大的液面翻转和液面破裂.粗网格在描述自由表面变形时缺乏准确性,导致俯仰力矩的偏差较大.因此可知,1.6 cm网格尺寸在精度和效率之间保持了良好的平衡,将在本研究中采用.
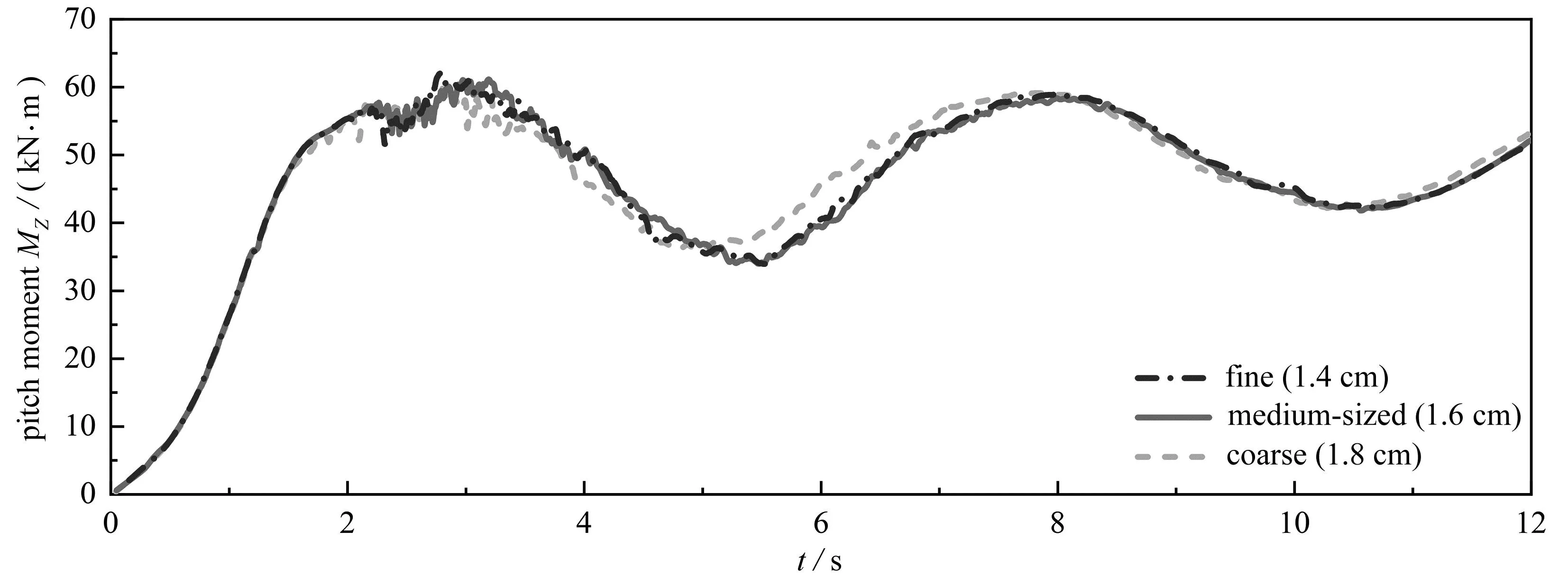
图8 三种不同网格尺寸的俯仰力矩时程比较Fig. 8 Comparison of time histories at pitch moments obtained for 3 different mesh sizes
3.2 合力和力矩
图9显示了不同储罐配置下纵向力的时间历程.结果表明,对于T0储罐,纵向力在1.6 s时达到最大值然后缓慢下降,即使在12 s时也表现出小振幅振荡.对于T1储罐,纵向力的峰值显著大于T0储罐的峰值,并且纵向力表现出更明显的振荡.原因是T1罐的单段弹性膜过长,导致液体和弹性膜之间产生了强烈的相互作用.但对于T2和T3储罐,随着膜长度的减小,纵向力的峰值急剧下降,纵向力时间历程迅速衰减,在4 s时即可达到稳态值.上述讨论表明,采用短长度的多段弹性膜而不是长的单段弹性膜,将对抑制液体晃动产生更明显的阻尼作用.

(a) 纵向力 (b) 频率 (a) Longitudinal forces (b) Frequencies
通过对纵向力的快速Fourier变换(FFT),得到了四种不同结构储罐纵向液体晃动的基频.结果表明,无论弹性膜的配置如何,安装有弹性膜的储罐的纵向基频都显著高于清孔储罐的纵向基频.具有不同弹性膜配置的三种类型储罐的纵向基频分别相对T0储罐增加了2倍、4倍和1倍.由于油罐车的纵向基本晃动频率约为0.2 Hz[25],添加弹性膜将使基频偏移到更高的值,以避免部分填充的液罐车发生共振.
在油罐车的制动操作过程中,液体的显著晃动可能会导致车辆载荷的不均匀分布.图10显示了不同储罐配置的垂向力的时间历程.在2.5 s时,在T0储罐中观察到显著的波谷值.在安装了弹性膜的储罐中没有观察到这种波谷值,并且垂向力变化的幅度明显小于T0储罐的垂向力变化幅度.图11显示了具有不同膜配置的储罐在2.5 s时自由表面的变形.从图11可以看出,T0储罐中的大量液体积聚在储罐右侧,并猛烈冲击储罐顶部导致液面翻转,这解释了图10所示垂向力的剧烈变化.通过对不同膜配置获得的垂向力和自由表面变形的比较表明,膜的添加可以有效地降低液体晃动的严重程度,从而有效地防止油罐车纵向载荷的不均匀分布.
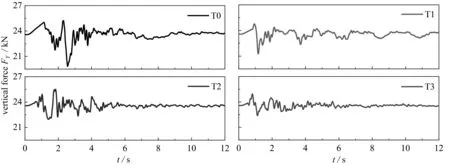
图10 不同配置储罐垂向力的时程比较Fig. 10 Time history comparison of vertical forces for different configurations of storage tanks

(a) T0 (b) T1
俯仰力矩是评价坦克车制动性能的一个重要指标.图12显示了具有和不具有弹性膜的储罐的俯仰力矩的时间历程.T0储罐的俯仰力矩在3 s时达到峰值,并在大范围内波动,这可能导致液罐车偏离运动方向.T1储罐的俯仰力矩在1.4 s时达到峰值,峰值比T0储罐低58%,并显示出相对较高的振荡频率,波动的幅度和平均值也显著降低.而T2和T3储罐的俯仰力矩峰值被有效消除.这是因为弹性膜将液体限制在膜下方的有限区域,限制了液体质心的转移.此外,由于T2和T3储罐使用了多段弹性膜,弹性膜间隙的位置比T1储罐更靠近右壁.液体的相互碰撞导致部分液体通过弹性膜间隙溢出,从而导致俯仰力矩缓慢上升.
图12 不同储罐配置俯仰力矩的时程比较Fig. 12 Time history comparison of pitch moments for different tank configurations
3.3 液体载荷转移
液体载荷转移是液罐车相比运输刚性货物的车辆更危险的一个重要因素[3].储罐中液体质心随时间的变化可以反映液体晃动的强度.图13显示了不同配置储罐的液体质心在纵向和垂向上的变化.很明显,T0储罐的液体质心位置随时间变化很大,无论是纵向还是垂向,而弹性膜的存在阻碍了液体在储罐中的流动.对T1、T2和T3储罐获得的液体载荷转移的比较表明,当弹性膜间隙的位置靠近储罐中心时,弹性膜抑制晃动的效果更显著.
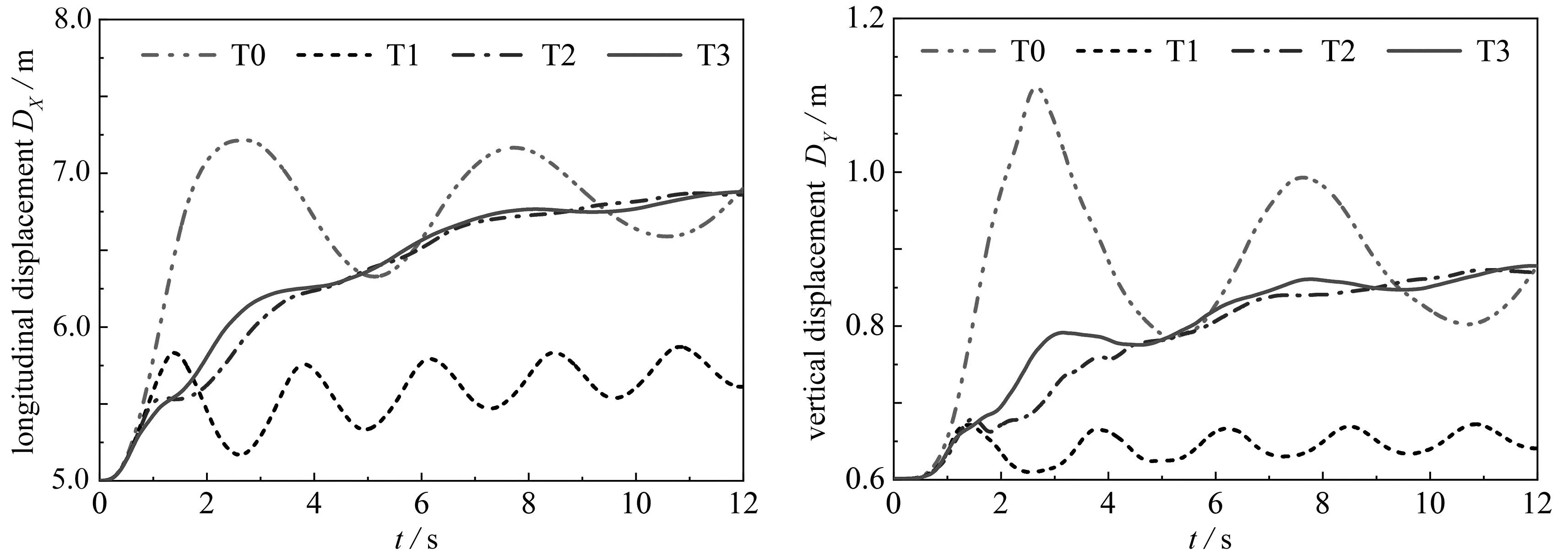
(a) 纵向位移 (b) 垂向位移(a) Longitudinal displacements (b) Vertical displacements
图14显示了不同配置下储罐中液体质心坐标的变化.可以发现,T0储罐中的液体质心可以到达储罐的右上角,并在较高的位置来回移动.在所有储罐配置中,T1储罐显示出最小的液体载荷转移范围.从图14中的局部放大图可以看出,质心位置呈现出往复变化,这导致了图12所示的俯仰力矩时程的高频振荡.相比之下,T2和T3储罐的液体质心显示出单向运动.这意味着液体被弹性膜包裹,并通过弹性膜间隙缓慢溢出并积聚在弹性膜上方.

图14 不同储罐配置液相质心坐标变化历史的比较Fig. 14 Comparison of coordinate change histories of liquid-phase mass centers for different tank configurations
3.4 罐壁压强
表1和表2分别比较了储罐右壁上不同高度位置的压强峰值和稳态值.弹性膜位于a/H=0.5处.结果表明,无论储罐配置如何,压强峰值都随着压强监测点高度的增加而减小.此外,当压强监测点的位置在弹性膜下方时,T1、T2和T3储罐的压强峰值均显著大于T0储罐.这是因为液体积聚在由膜和罐壁包围的空间中,与T0罐相比产生了更高的液体压强.当压强监测点的位置在弹性膜上方时,T1、T2和T3储罐的这些监测点的峰值压强均显著低于T0储罐的峰值压强.这是因为膜的添加抑制了液体在弹性膜以上位置处的流动,使得这些监测点的峰值压强接近于零.对于压强稳态值,可以得出相同的结论.由于在稳态时,液体表现出轻微的晃动,T1、T2和T3储罐的弹性膜以下位置处的稳态压强均略大于T0储罐的稳态压强值.
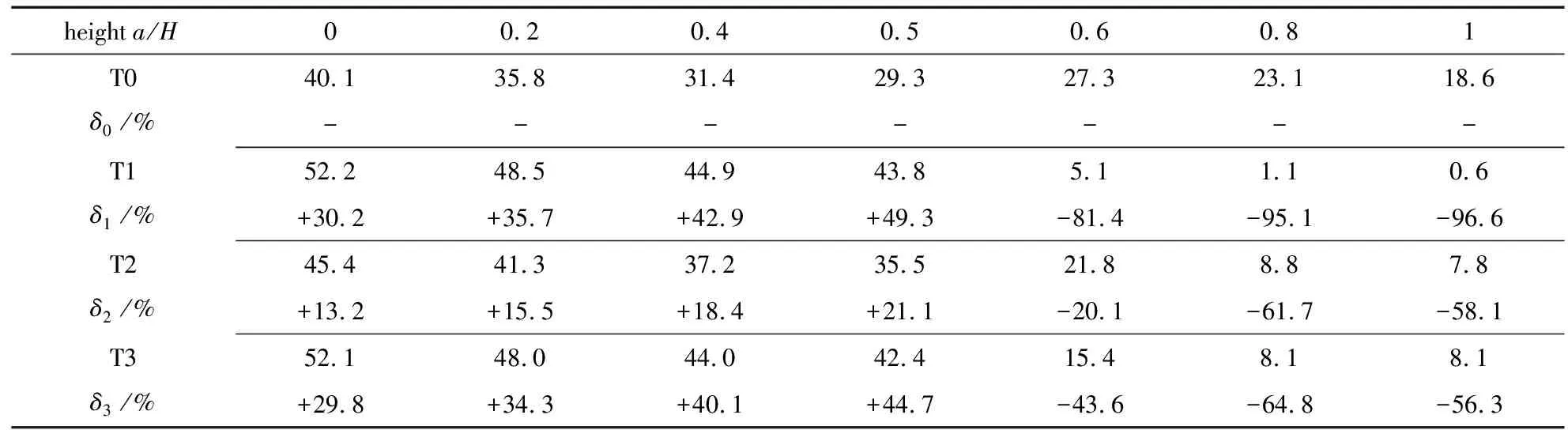
表1 右壁上不同高度位置(a)的压强峰值时程比较

表2 右壁上不同高度位置(a)的压强稳态值时程比较
4 结 论
本文建立了一个流固耦合模型,研究了二维部分填充矩形储罐中不同弹性膜配置的抑制晃动效果.通过数值计算结果与实验室实验结果的比较,验证了该模型的有效性.验证后的数值模型被进一步用于研究膜的数量对抑制液体晃动的影响.通过将弹性膜在力、力矩和液体载荷转移方面的晃动响应与无膜储罐的晃动响应进行比较,评估了弹性膜的抑制晃动效果.一些结论可以总结如下:
1) 数值结果与实验结果吻合较好,证明了数值模型的有效性.
2) 膜的加入使晃动力的时间历程衰减得更快.然而,在某些情况下,由于液体和弹性膜之间的相互作用,膜的存在会增加晃动力的峰值.
3) 随着膜段的增加,纵向力的峰值急剧下降,纵向力时程衰减更快,这意味着采用短长度的多段弹性膜而不是长的单一弹性膜将对抑制液体晃动产生更明显的阻尼作用.
4) 弹性膜的加入将显著降低俯仰力矩的峰值,这将显著提高液罐车的制动性能.
5) 弹性膜的存在阻碍了液体的运动,抑制了液体载荷的转移,这将在一定程度上缓解纵向载荷分布的不均匀.
