柱状螺纹直线超声电动机结构设计与实验研究

秦鸿飞,王中营,宋勇宏,张高任,游 蕾

(河南工业大学 机电工程学院,郑州 450001)

0 引 言

超声电动机是20世纪80年代发展起来的新型驱动电机,利用压电材料的逆压电效应,激发定子在超声频段内产生微幅振动,通过摩擦实现动子的宏观运动[1]。柱状直线超声电动机具有结构简单、无电磁干扰、功率密度高、断电自锁、适合微型化等优势,在光学仪器、精密工程等领域有广阔的应用前景[2-3]。柱状直线超声电动机因其特有的优势,受到国内外研究学者的广泛关注。文献[4]提出一种螺纹副驱动超声电动机。文献[5]研制出基于弯振模态的微型直线超声电动机并将其运用到微控制系统中。文献[6]提出的微型直线超声电动机,通过两个金属的摩擦来实现直线运动。文献[7]研制的柱状双足驱动直线超声电动机,采用柱体两端驱动足的三阶弯曲模态实现驱动,电机最高速度超过20 mm/s,最大负载11 N。文献[8]提出一种多面体螺母型超声电动机,粘有压电陶瓷的多面体铜管作为定子,动子的外螺纹与定子的内螺纹相互啮合,通过定子产生2个面内弯曲模态实现驱动。文献[9]提出一种直线超声电动机,采用分体式结构,解决了螺纹直线电机定子和动子之间预压力施加的难题。

柱状直线超声电动机大多是利用柱体轴向的弯曲振动模态,定子多为细长状,空间适配性较差,为了改善螺纹直线超声电动机定子结构刚度,降低谐振频率以及提高电机输出力和空间适配性,将现有柱状螺纹超声电动机定子进行结构设计。基于机械原理螺纹传动和机械振动的相关知识,提出一种在电机定子内壁进行开槽处理的设计方案,通过结构设计改善振动体的模态特性,提高驱动点的位移响应,之后利用定子的两个相互正交的面内三阶弯曲模态和螺纹传动相配合,实现电机的转动[10]。

1 电机结构设计与驱动原理

1.1 电机结构设计

柱状螺纹直线超声电动机主要由定子基体和动子组成。定子基体由开有内螺纹的中空金属方柱体和4片压电陶瓷组成,并通过环氧树脂胶粘贴为一整体。定子基体材料为黄铜,经过前期的分析与对比,确定定子基体的长、宽、高分别为10 mm×10 mm×9 mm,中心加工M8×1 mm的螺纹通孔,整体结构如图1所示。

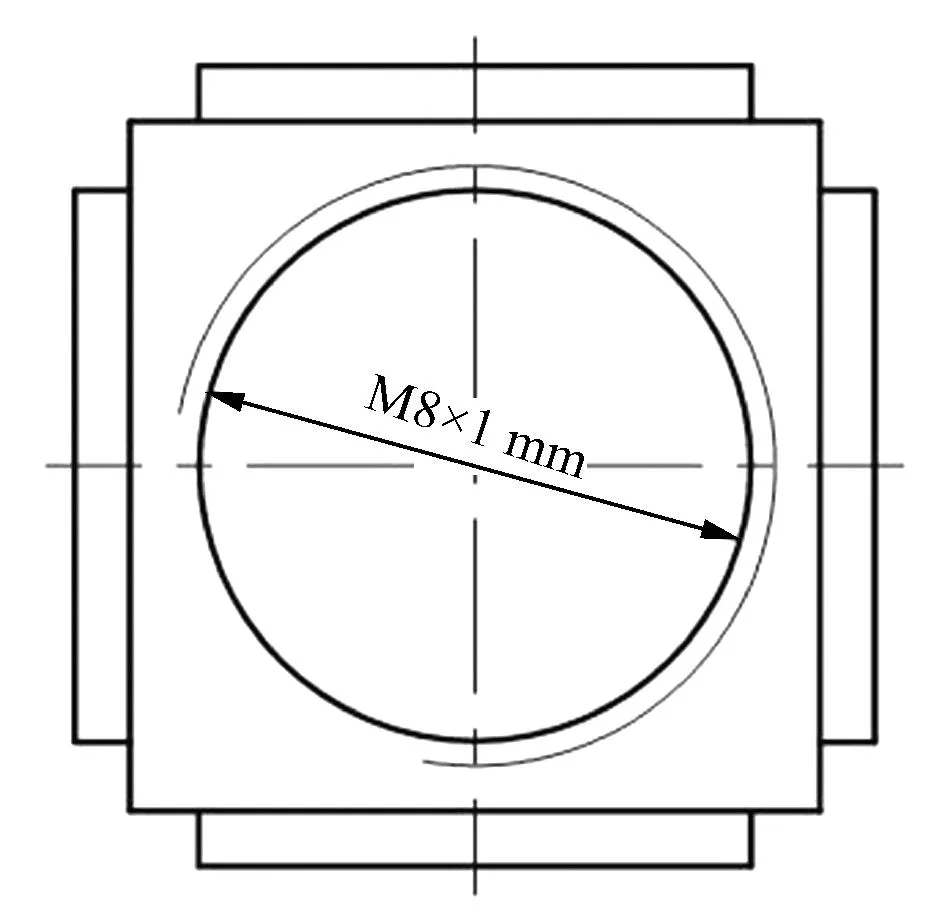
图1 定子基体主要参数

在螺纹传动过程中,通过内螺纹和外螺纹的牙面相接触来传递力矩,由于定子的内螺纹和动子的外螺纹刚度和形变不同,即使采用高精度设备进行加工,各个螺纹环上的受力也各不相同,往往只有旋合的第一圈处受力最大,后端螺纹传递力矩依次减小。为了改变电机定子的结构刚度,降低其谐振频率,增加电机输出力;同时考虑到柱状螺纹超声电动机的起停及换相问题,从定子螺纹内壁中央部分进行开槽L处理,开槽位置如图2所示[11]。

图2 定子基体开槽位置示意图

设定定子凹槽内径为9 mm,研究不同槽宽L对定子谐振频率的影响。为保证定子螺纹和动子螺纹间的接触面积,槽宽L的变化区间设定为0～4 mm,每隔0.5 mm对定子进行模态分析,并对分析的数据进行记录整合,绘制结果如图3所示。

图3 定子频率随凹槽宽度响应曲线

由图3的槽宽-频率变化曲线可知,定子工作模态频率随凹槽宽度的增加而逐渐降低,同时左右相邻模态频率也随着电机工作频率的降低而降低,两者的差值变化较小,对电机工作模态不产生干扰。据此可以确定开槽的几何参数,其中槽底直径为9 mm,槽宽为4 mm。

动子采用不锈钢材质,外螺纹为M8×1 mm,内孔直径为6 mm,总长为12 mm。

压电陶瓷材料为PZT-4,长、宽、高分别为8 mm×7 mm×0.8 mm,沿厚度方向极化,采用d31振动模式。将定子面对面的一对压电陶瓷定义为A组,另外一对定义为B组,压电陶瓷的粘贴方式、极化方向和分组情况如图4所示。

图4 压电陶瓷粘贴方式和极化方向

1.2 驱动原理

同时给A、B组压电陶瓷施加同频同幅且相位差为90°的激励电压,A、B组分别激励出一个驻波,这两个驻波叠加后形成为一个行波,行波沿逆时针方向行进[12],如图5所示。选取P点为研究对象,当t=0时,P点位于行波的波谷位置,如图5(a)所示;当t=T/4时,P点位于节点位置,如图5(b)所示;当t=T/2时,P点位于波峰位置,如图5(c)所示,此时定子驱动面与动子外螺纹面接触,通过摩擦力推动动子沿顺时针方向转动;当t=3T/4时,P点重新回到了节线位置,如图5(d)所示;当t=T时,P点回到原点,此时P点完成一个运动周期,P点的运动轨迹为一个椭圆,以此来驱动转子运动。

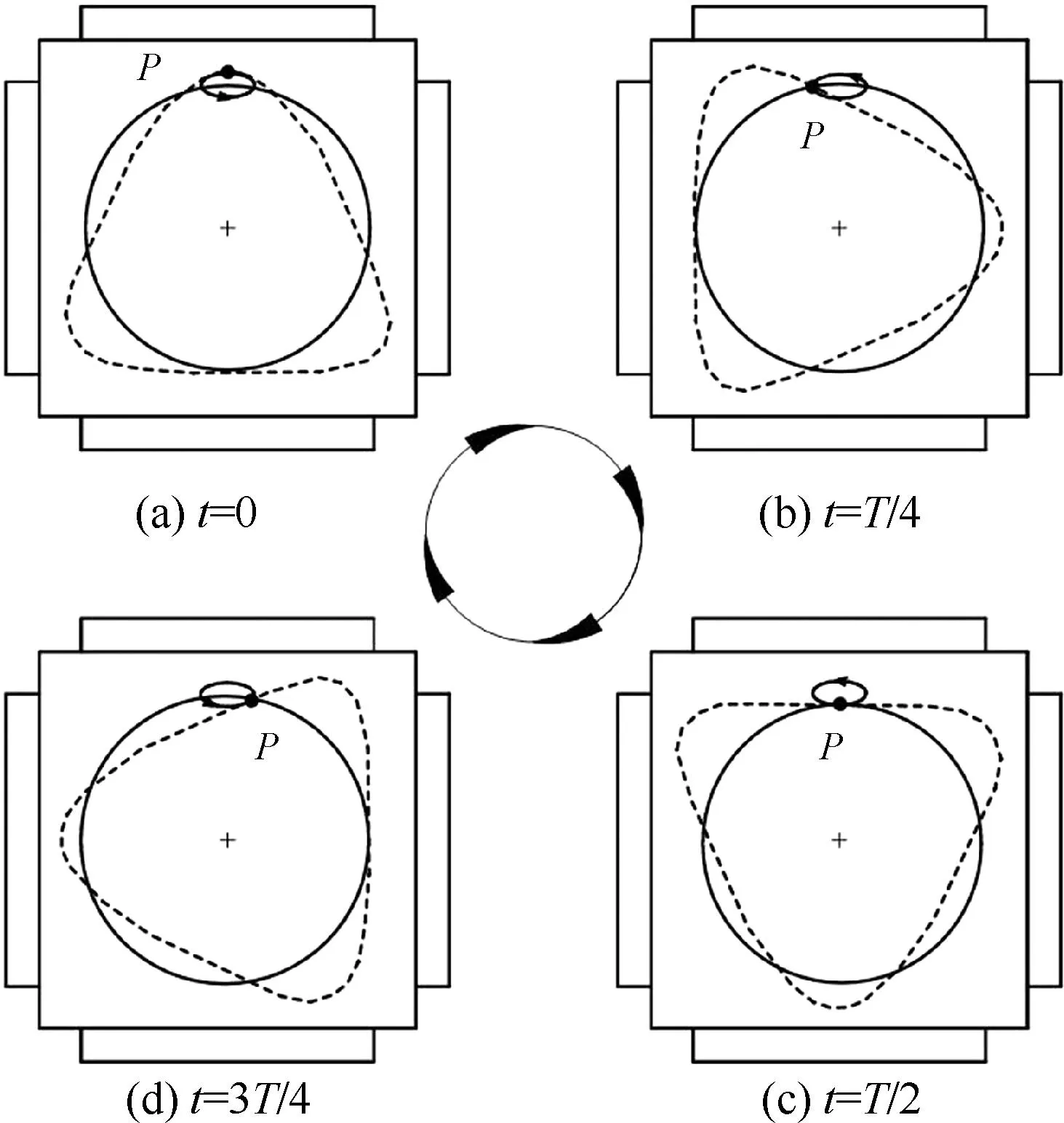
图5 质点椭圆轨迹形成过程

2 结构动力学分析

2.1 定子有限元模型

为了研究开槽后定子的振动频率和驱动点的位移响应改变情况,采用有限元软件ANSYS Workbench对开槽后的定子进行结构动力学分析,采用六面体单元对定子基体和压电陶瓷进行网格划分,有限元模型如图6所示。

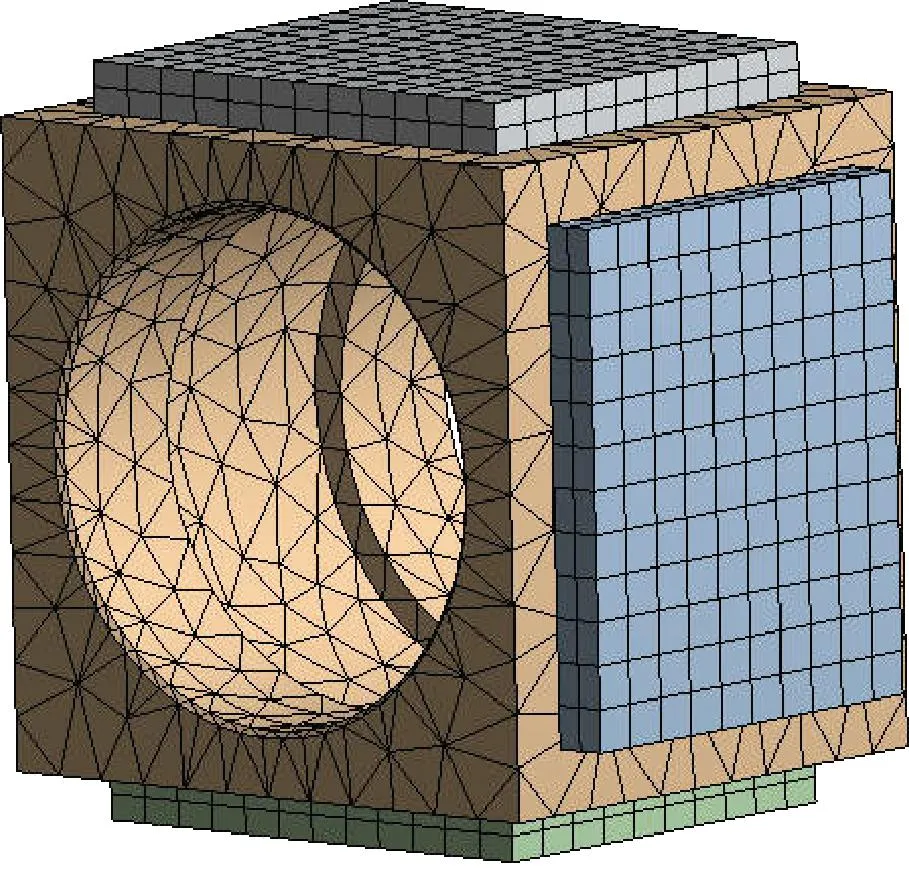
图6 定子有限元模型

分析过程中所涉及的材料参数如表1所示。

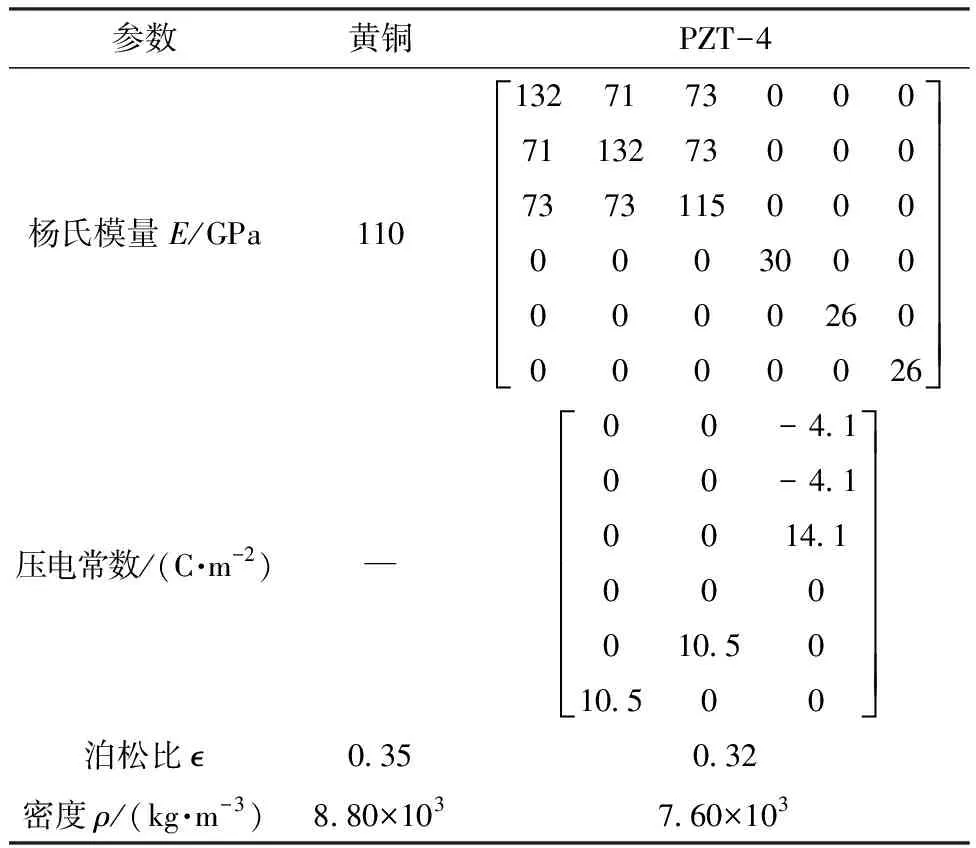
表1 定子材料参数

2.2 模态分析

为分析开槽设计对定子的模态振动频率改变情况,将建立好的几何模型导入到Model分析模块中,输入相关材料参数,定子保持自由边界约束条件,为尽可能多的分析定子各模态的变化情况,将模态阶数设定为20,从分析结果中提取出两个正交的三阶面内弯曲模态,如图7所示。

两模态的共振频率分别为76.385 kHz和76.392 kHz,差值仅为7 Hz,共振频率接近。相比于开槽前定子X方向和Y方向的共振频率83.462 kHz和83.537 kHz,分别降低了7.077 kHz和7.145 kHz,共振频率的差值也降低了68 Hz,两相工作模态频率一致性有了显著提高,同时共振频率的降低减少了高频振动导致的定子压电材料的疲劳损坏。由此可见,对定子螺纹内壁进行开槽处理的设计方案,可以降低电机的电源功耗,减少定子发热量,提高电机工作效率,延长电机的使用寿命。

2.3 谐响应分析

谐响应分析用来反映系统受到周期性变载荷作用下的稳态响应。为研究定子弹性体在开槽处理后变载荷作用下的稳态响应情况,对定子进行谐响应分析,保持自由-自由的边界约束条件,分别给A、B组压电陶瓷施加相位差为90°、峰值幅值为100 V的激励电压,分析开槽后定子谐振频率点的变化情况。

结果如图8所示,开槽后定子的X向和Y向谐振频率点均接近76.88 kHz,相较于开槽前的复合谐振频率点83.88 kHz,开槽后的共振频率点降低了7 kHz,同时位移响应输出也从8 μm提高到了10 μm,提高了约25%。位移响应越大,表明定子对转子的驱动能力越强。由分析结果可知,开槽处理后定子螺纹内壁驱动点的振幅有所提高,超声电动机的驱动能力进一步增强,同时在该频率附近无其他干扰模态频率,可以用该频率驱动电机。

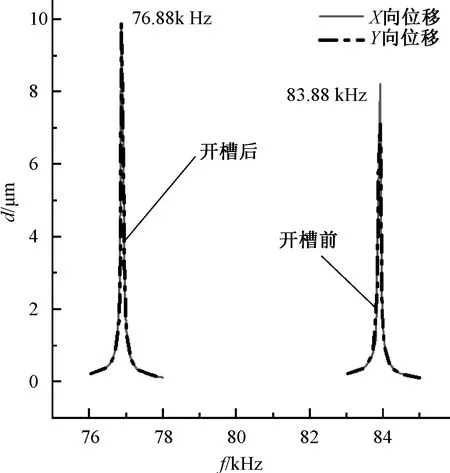
图8 定子开槽前后位移响应对比

2.4 瞬态分析

为研究定子内壁驱动点的瞬态运动轨迹变化,对其进行瞬态动力学分析。采用命令流的方式对A、B组施加频率为76.88 kHz、峰值幅值为100 V、相位差为90°的激励电压,提取定子内表面P点沿X、Y向的瞬态位移。

由图9可知,随着电压持续不断的激励,定子工作模态逐渐得到激发,定子内壁P点沿X、Y向位移均逐渐增大,经过一定周期的运转后,P点运动轨迹形成稳定的椭圆。

图9 定子内P点运动轨迹

3 实验研究

3.1 样机试制与定子阻抗分析

根据上述分析结果,对定子进行图纸绘制,加工定子,采用型号为JA203的电子质量测量仪器分别测试开槽前后的电机定子质量。结果显示,开槽后的定子相比于未开槽的定子质量减轻0.4 g,同时订购压电陶瓷片,组装零部件,完成样机装配,如图10所示。

图10 样机实物

采用型号为PV70A的阻抗分析仪对电机定子A相和B相进行阻抗测试,将样机两相信号输入端口依次接入阻抗分析仪,分别测试其阻抗,参考上述谐响应分析结果,设定扫描频率为73～88 kHz,并对阻抗测试的数据进行整合,整合结果如图11所示。

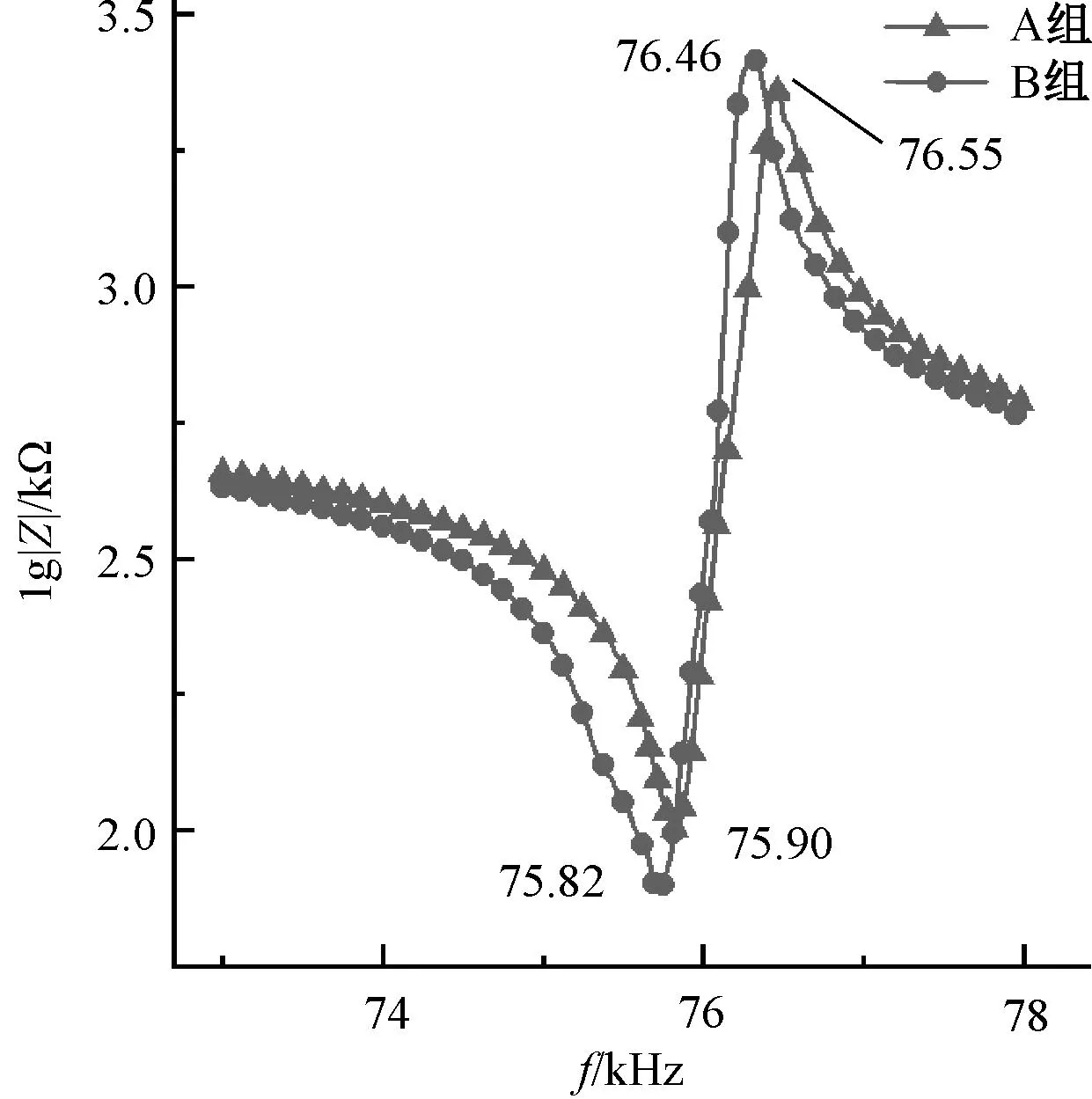
图11 样机阻抗测试结果

由图11可知:A组共振频率为75.82 kHz,反共振频率为76.46 kHz;B组共振频率为75.90 kHz,反共振频率为76.55 kHz。两组共振频率差值较小,数值略低于上述有限元分析结果,误差可能来源于:有限元分析时未考虑胶层对样机振动的影响;定子和压电陶瓷的加工和装配有误差;计算所用材料属性和实际数值有所出入,两者的误差较小,在可接受范围内。

3.2 样机性能测试

采用型号为LYC-400D的超声功率放大器以及RIGOL-DG1032型号的信号发生器给电机定子提供两相电压信号,同时使用德国SICK公司型号为ODI-B035H15U25的高精度位移传感器与STM32 单片机以及PC机组成的测试系统对电机的各项性能进行测试。

3.2.1 频率-速度特性

首先确定电机的最佳工作频率,在频率-速度特性测试中可以较好地确定电机的最佳工作频率,在样机负载0.5 N的情况下,施加峰值幅值为90 V、相位差为90°的电压,在频率范围为74.8～75.6 kHz时,电机开始运行,测试结果如图12所示。

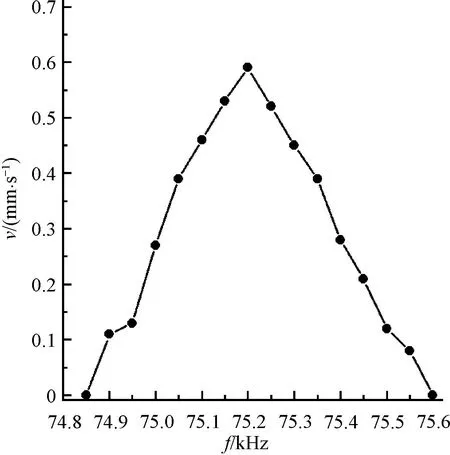
图12 频率-速度特性曲线

随着输入信号频率不断增加,电机的速度呈先增大后减小的变化趋势,当输入电压信号频率为75.2 kHz时,电机运行速度达到最大,最大速度为0.59 mm/s,相比于电机定子未开槽优化前0.45 mm/s的速度最大值,提高了31.1%。

3.2.2 相位差-速度特性

确定了定子的最佳工作频率为75.2 kHz后,同样施加负载为0.5 N,峰值幅值为90 V的电压信号,用信号发生器调节两相信号的相位差在0～180°的范围内变化,实验结果如图13所示。

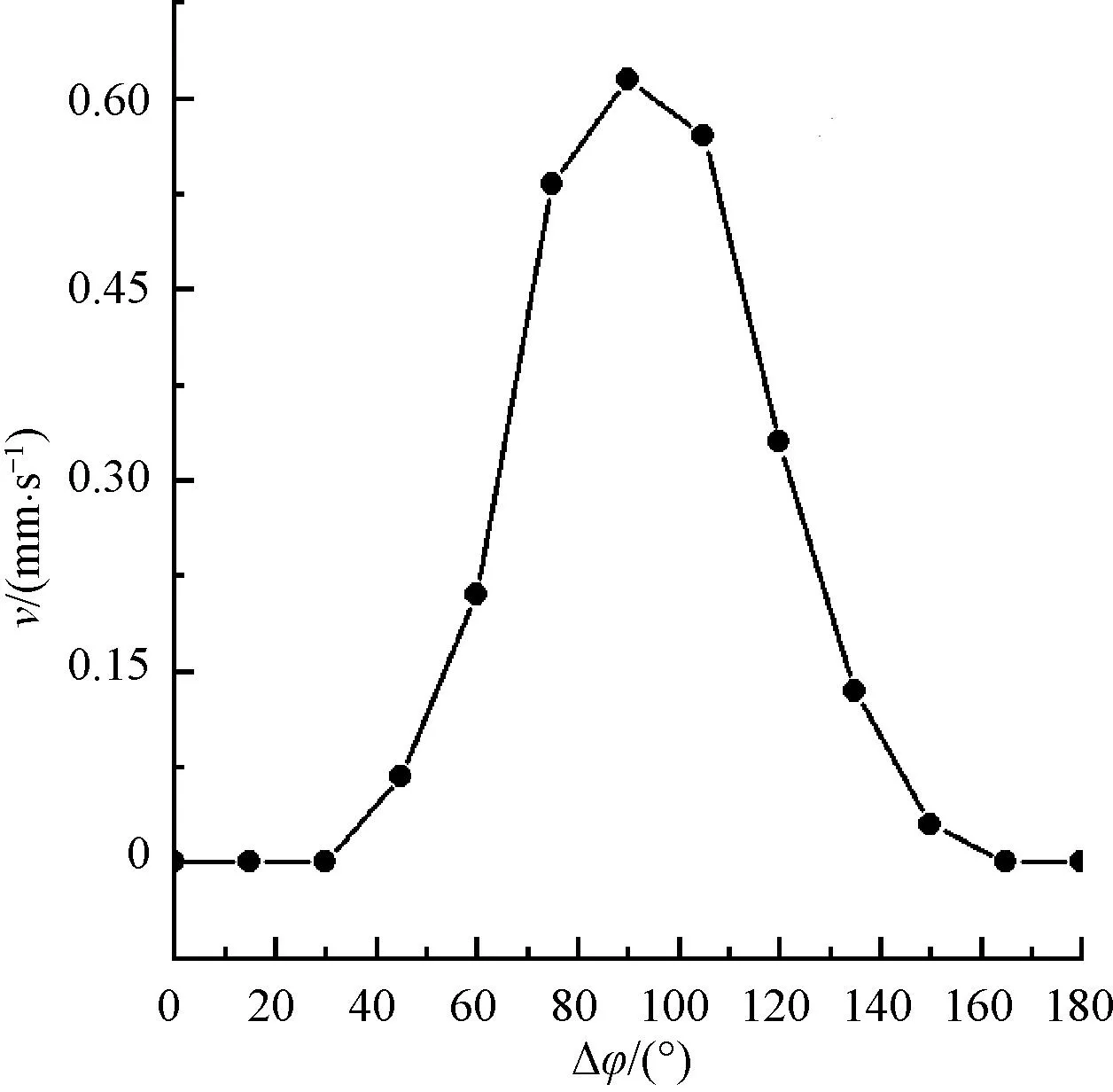
图13 相位差-速度特性曲线

电机在两相输入信号相位差为30°～150°的范围内均可实现运转,在30°～90°以及90°～150°间调速线性度较好,同时相位差对电机速度的调节作用基本呈对称形态,当相位差为90°时电机运转速度最大,与上述的理论分析相契合。

3.2.3 负载特性实验

负载特性的性能指标对电机的实际应用场景具有重要参考意义。在实验室条件下,通过在电机转子上悬挂不同质量的砝码来给电机动子施加负载,测试实物如图14所示。

图14 负载测试实物

为了测得电机平稳运行条件下的最大输出力,将电机的输入电压幅值进行上调,然而过高的电压幅值和频率将导致定子发热量过大,从而导致压电陶瓷退极化,故将电机的输入电压峰值幅值增加到130 V,驱动频率为75.2 kHz,相位差为90°,测试电机的最大输出力,结果如图15所示。

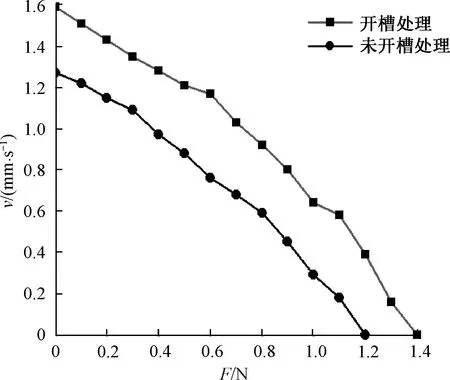
图15 输出力-速度特性曲线

随着负载的增大,电机的速度近似线性下降,最大输出力为1.4 N,相比于开槽前1.2 N的最大负载,电机最大输出力提高了16.7%,推重比提高了30.8%。

4 结 语

本文设计了一种柱状螺纹副驱动直线超声电动机。电机定子基体为方柱结构,将定子内壁进行开槽处理,通过粘贴于方柱基体上的4片压电陶瓷,激励定子产生两个相互正交的三阶面内弯曲模态,在定子驱动面叠加形成行波,驱动动子运动。采用有限元方法对开槽后的电机定子进行了分析,确定开槽宽度,提取定子的工作模态,计算出定子的谐振频率及驱动点运动轨迹。

研究表明,对定子内螺纹进行部分开槽处理能够改善定子的振动特性,对定子内螺纹开槽处理能够降低定子结构刚度,减小谐振频率,提高位移响应。

制作样机,搭建测试平台并开展实验研究。结果表明,开槽处理后的电机最大运行速度为0.59 mm/s,最大推力为1.4 N,分别提高了31.1%和16.7%。开槽后的电机最佳工作频率降低了7 kHz,位移响应提高了25%。本文的研究对于减少压电材料的振动疲劳损坏,降低电机的内部机械损耗和电源功耗,提高电机工作效率和寿命具有借鉴意义。