RaptorQ喷泉码编译码算法分析及优化
2024-03-27马梦宇罗长洲梁春瑞
马梦宇, 罗长洲, 梁春瑞, 王 杰
(1. 北京控制与电子技术研究所, 北京 100038; 2. 中国航天科工集团二院研究生院, 北京 100854)
0 引 言
喷泉码作为一种新兴的前向纠错码,其优势体现在“无码率性”[1-2]、“鲁棒性”和“独立于信道删除概率特性”。喷泉码的编码器如源源不断产生编码数据包流的“喷泉”,译码器接收到一定数量的编码数据包后,就可以以极高的成功率恢复出源码信息。从理论上讲,编码端可以源源不断地产生编码数据包,而译码端没有固定的接收编码数据包的数量,所以称喷泉码具有无码率特性。喷泉码数据结构灵活,可以根据信道状态调整编码包生成数量和接收端的实际接收需要,具备很好的鲁棒性[3-4]。喷泉码能否成功译码只取决于译码端收集到的“喷泉”的数量,与“喷泉”在信道上的损失无关,其独立于信道删除概率特性,使喷泉码能够自适应于时变信道状态的变化,在信道状态未知的数据传输[5]和多媒体分发网络中具备良好的传输性能。
喷泉码设计的初衷是解决删除信道上的数据分组传输问题,随着研究的逐渐深入,喷泉码的应用场景也在逐渐拓展。除了删除信道,喷泉码在加性高斯白噪声和衰落信道下也能发挥很好的性能。喷泉码已经被广泛应用于各类场景中[6-8]。
自2002年LT(Luby transform)码被提出,在其基础上依次出现了Raptor[9-10]码和RaptorQ[11]码,并在高通公司的推广下分别将Raptor码和RaptorQ码写入国际标准RFC5053和RFC6330,喷泉码的编译码算法[12-14]是重要的研究方向之一。由于在实际应用中,喷泉码的符号长度存在上限,文献[15]就LT码的设计及其有限长度进行了分析;度的分布计算同样影响喷泉码算法的性能,诸多学者[16-19]对喷泉码的度分布计算方法展开了研究;文献[20]推导了以最大似然解码算法为基础的Raptor码解码失败概率的上限和下限。
RaptorQ码是以LT码和Raptor码为基础进一步发展的最新研究成果,针对RaptorQ码的研究是这3类喷泉码研究中最少的,整理后发现,RaptorQ码的性能在喷泉码中没有清晰的定位和评估,对于RaptorQ码复杂度较高这一问题,也没有相对合理的解决方案。文献[21]利用降维变换,将需要计算的逆矩阵转化为维度更小的矩阵求逆,以此简化RaptorQ码的译码复杂度,但该算法需要在删除概率较小(小于0.2)的信道中才能发挥作用;文献[22]提出基于消元方式的编码算法来规避编码过程中需要的矩阵乘法,但是其推出的矩阵预先求逆算法仅适用于编码时A矩阵为方阵的情况,对于算法消耗时间占比很大的译码端来说并不适用;文献[23]提出一种模式选择解码算法,需要提前对信道的状态进行探究,而模式选择器的设计策略也将影响喷泉码编译码算法的效率,在一定程度上弱化了喷泉码的自适应能力。
基于上述分析,本文从LT、Raptor及RaptorQ码的角度,采用理论分析加仿真验证的方法将三者进行横向对比,以此对RaptorQ码的性能和编译码复杂程度进行全面的评估。针对RaptorQ码编译码复杂度高的问题,以RFC6330编译码方案为基础,在保证性能不变的前提下,通过固定生成矩阵A,通过提前列变换和去稀疏化对其编译码算法进行优化,并通过仿真实验和对比分析验证了方法的可行性和有效性。
1 RaptorQ编译码算法分析
1.1 LT码编译码算法
LT码是第一种实用数字喷泉码,其具体编译码过程如下:在每产生一个编码符号之前,先由度分布函数生成该编码符号的度d,随后根据度值,随机选取d个原始的信息位进行异或运算,运算结果即为所要传输的编码符号。待接收端接收到编码符号之后,一般采用高斯消元(Gaussian elimination, GE)法译码,即GE译码算法,将编码符号与原始信息位之间的关系用矩阵的形式表现出来。由于每个编码符号通过原始信息位异或生成,对应于生成矩阵,就是在该行相应的位置置1,将原始信息位和接收到的编码符号以列向量的形式表示出来,就可以得到以下关系式:
G×F=E
(1)
式中:G是生成矩阵,矩阵元素仅由0和1组成;F为原始信息位组成的列向量;E为接收到的编码符号组成的列向量。译码问题转化为已知G和E,求解线性方程组解出F的问题。采用GE法,将G矩阵转化为单位矩阵,得到原始信息位的值,即译码成功。
从整体的编译码算法角度观察LT喷泉码,其编译码算法较为简单,计算复杂度与码长K呈现非线性关系:
O(KlgK)
译码失败的错误下限较高,为了较好地覆盖到所有原始信息,增加成功解码概率,需要设置一定数量的度值较高的编码符号,这增加了系统的异或计算次数,一定程度上增加了编译码复杂程度。为解决上述LT喷泉码高误差下限问题,降低编解码复杂度并实现线性编解码,在此基础上设计增加了预编码手段,即Raptor码。
1.2 Raptor码编译码算法
Raptor码可看作一种级联编码方式,是在LT码的基础上,增加了预编码的过程。源码首先以预编码的方式生成带有一部分冗余信息的中间符号,再将中间符号通过弱化的LT编码产生编码符号。所谓弱化的LT编码,是指规避上述LT码产生高连接度值的编码符号,尽量弱化由中间符号生成编码符号过程的度值,这样做的好处是减少异或计算次数,后果是导致译码过程中,由于对中间符号覆盖度不高,无法完整地恢复所有中间符号,不过未被恢复的中间符号只占一小部分,且中间符号在生成时就具有一部分冗余位,可根据预编码的纠错能力,将完整的原始信息从中间符号中恢复出来。Raptor码以预编码加弱化的LT编码形式,加强了喷泉码的纠错能力,减少了计算复杂程度,同时实现了线性编解码,其编解码算法复杂度为
O(Klg 1/ε)
式中:ε为译码冗余。
1.3 RaptorQ码编译码算法
RaptorQ喷泉码是在Raptor码基础上的进一步提升,在预编码和译码算法等方面均采取了更为复杂的计算方式,旨在将译码冗余信息减少到最低限度,同时拓展喷泉码的使用条件:RaptorQ码最大源符号长度从Raptor码的8 192 拓展到了56 403;可产生编码符号数量的上限也从216拓展为224,增加了256倍;生成矩阵A的元素从0和1变为0~256;运算范围从伽罗华域(Galois field,GF)(2)变为GF(256)。根据有限域GF(q)的分析,有:
q=pn
(2)
式中:p是素数;n是大于0的整数。
在GF(q)的任意有限域上,喷泉码的解码性能存在如下理论极限:
(3)
式中:Psuccess为成功解码概率的理论极限;O为译码冗余。
可以看到,在译码冗余相同的条件下,q越大,成功解码概率的理论极限越高。但是编译码复杂程度也在随之增加,即使RaptorQ很巧妙地将高效GF(256)算法和低复杂度GF(2)算法结合起来,尽可能减小GF(256)的辐射范围,降低编码时的计算复杂度,译码时算法复杂度的急剧增加仍不可避免。采用了优化失活高斯译码算法的RaptorQ编译码复杂度为O(L2),其中L为RaptorQ码产生的编码符号的长度。
1.3.1 RaptorQ的编译码流程
图1为RaptorQ喷泉码编绎码的数据流图。

图1 RaptorQ编译码流程Fig.1 RaptorQ encoding and decoding flowchart
RaptorQ喷泉码编译码步骤分为3步:参数初始化、预编码和编码。
首先以补零的方式将K个源符号拓展为K′,该扩展的目的在于最小化编译码过程中信息的存储量,加快编译码速度,以K′为输入,计算得到构建预编码生成矩阵A的一系列参数。
预编码阶段,A矩阵行列值的数量关系由K′决定,在参数初始化体现,满足如下关系:
L=S+H+K′=B+S+U+H
(4)
使A矩阵成为L×L的方阵。根据图2中的RaptorQ译码公式,A矩阵代表中间符号C向量与源符号D向量的线性关系,利用A矩阵和源符号向量D两个已知条件,即可解出中间符号向量C。
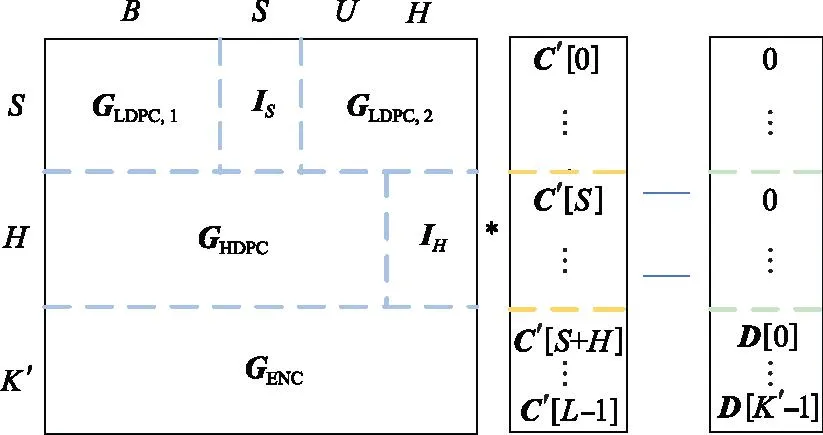
图2 RaptorQ译码公式Fig.2 Formula of RaptorQ decoding
中间符号向量C为预编码阶段的输出,将其成功解码的前提条件为生成矩阵为列满秩矩阵。将其进行LT编码,得到最终输出的编码符号,该编码符号由源码与修复码组成。编码符号的数量N可根据所需的速率和预期的信道丢包概率提前设置。
译码是编码的逆过程,编码符号经过信道后,译码器整理好接收到的编码符号,再次进行参数初始化和预编码阶段处理,对于译码阶段的预编码矩阵RecA,除第3层GENC矩阵的行数外,其他参数与编码阶段生成的矩阵A一致。
在RaptorQ编译码中,最核心也是计算复杂度最高的部分是利用A和RecA矩阵通过解线性方程组求取中间符号的这一过程,在RFC6330中采用优化失活GE解码法,通过将矩阵分块,将GE过程限定在较小的范围内,分5个阶段将生成矩阵处理为单位矩阵,将中间符号向量和源符号向量进行相应的变换,则变换后的中间符号的值即为源符号的值。接下来以译码时M×L的生成矩阵RecA为例,详述失活解码GE法。
1.3.2 失活解码GE法
图3所示为RaptorQ失活解码GE法的流程图。

图3 RaptorQ失活解码GE法Fig.3 RaptorQ deactivation decoding GE method
失活解码GE法共分为5个阶段,首先根据非负参数i和u,以及RecA的行列值M、L,将RecA矩阵在概念上划分为多个子矩阵,进行第一阶段(即算法核心阶段的操作)由寻找标准行和GE两部分组成,值得注意的是,高密度奇偶校验(high density parity check, HDPC)行不在标准行的选取范围之中,这也是RFC6330设计标准行选取的原因所在,除HDPC行之外的所有行均定义在GF(2)上,选取GF(2)以及非零元素个数最小的行作为GE的标准行,就能最大限度地降低GE的计算次数。在第一阶段开始之前,将RecA矩阵复制,设其为X矩阵,直到GE过程之前,保持与RecA矩阵相同的操作。
第二阶段是使用Uupper子矩阵对Ulower子矩阵进行GE的过程,将Ulower矩阵的前u行消元为单位矩阵。
由于Uupper子矩阵非零元素较为密集,RFC6330设计第三阶段对Uupper子矩阵进行稀疏化,对于在第一阶段生成的矩阵X,取其前i行i列的稀疏下三角方阵Xi,与RecA矩阵的前i行进行相乘,将Uupper子矩阵稀疏化。

需要注意的是:
(1) 译码算法只是聚焦于RecA矩阵上,对于在RecA矩阵上的行列变换及消元等操作,中间符号向量C和源符号向量D要进行相应的变换;
(2) 不同于基本的矩阵运算,RFC6330中矩阵运算基于有限域GF(256)的运算法则,以异或、查表等操作对应于实数集的加减乘除运算法则。
2 喷泉码编译码算法仿真分析
喷泉码基于增加冗余位原理来对抗信道干扰,以增加译码开销的方法提高可靠性,所以,在同等条件下,保证相同误码率所需要的译码开销数量成为衡量喷泉码性能的重要指标。从LT码发展为Raptor码再到RaptorQ码的出现,喷泉码以降低译码开销为核心思想不断改进和优化,在实现这一核心思想的过程中,很可能造成喷泉码编译码算法复杂程度的提高,造成喷泉码性能和系统处理时延的相互制约。
为对比验证3种编译码算法的性能优劣,基于Intel(R) Core(TM) i5-3470 CPU @ 3.20 GHz~3.2 GHz和Matlab R2016b环境(本文实验均以此环境为背景)进行信道随机删除,删除概率为0.1;试验次数为105;码长K=128;译码冗余变化的仿真试验,实验结果如图4所示。

图4 译码冗余不同时3种算法的误码率对比Fig.4 Comparison of bit error rate of three algorithms with different decoding redundancy
喷泉码最耗时的操作为对生成矩阵求逆,据统计,码长K=4时,求逆过程耗时占用了整个编解码过程耗时的99%,码长K=1 024时,求逆过程耗时占用了整个编解码过程耗时的95%。而在求逆过程中,异或运算是运行次数最多、最核心的运算。为对比验证3种算法的编译码复杂程度,设置信道随机删除概率为0.1;译码冗余为0.15;试验次数为105;通过码长从128~2 048变化的仿真试验,统计3种算法程序的总异或次数。仿真实验结果如图5所示。

图5 码长不同时3种算法的总异或次数对比Fig.5 Comparison of total XOR times of three algorithms with different code length
为进一步对比验证3种算法的编译码复杂程度,进行信道随机删除概率为0.1、译码冗余为0.15、试验次数为105、码长从128~2 048变化的仿真试验。统计3种算法的平均编解码时长,实验结果如图6所示。

图6 码长不同时3种算法的编译码时间对比Fig.6 Comparison of encoding and decoding time of three algorithms with different code lengths
从图4可以看出,在相同的译码冗余条件下,LT编码的系统误码率最高,若达到相同的误码率,采用LT编码所需的译码冗余是最多的,且其误差下限较高;其次是Raptor码;所需译码冗余最少的为RaptorQ码。仿真数据表明,译码冗余在0.11以上时,RaptorQ码就可以达到99%以上的成功解码概率。
从图5可以看出,RaptorQ码的异或计算次数高于Raptor码和LT码,其次为LT码,最次为Raptor码。这是因为Raptor码采用预编码方式,规避了高连接度值的情况,减少了系统的总异或次数。RaptorQ码对码长进行了0拓展处理以及对生成矩阵的元素进行了改变,增加了码长以及生成矩阵维度,进而增加了编译码过程中的总异或次数。
从图6可以看出,在码长相同时,RaptorQ码的编译码时间远远高于LT码和Raptor码,这一结论与理论分析一致,三者的编译码复杂度依次为:O(KlgK)、O(Klg 1/ε)、O(L2)。在码长K增加时,RaptorQ码耗时曲线上升幅度最大,编译码耗时急剧增加。另一方面,RaptorQ中的异或运算的元素为GF(256)域中的元素,异或运算时间远远高于GF(2)域中的元素异或运算时间,以至于相比于LT码和Raptor码,RaptorQ码的编译码耗时与二者存在数量级的差距。三者比较,编译码用时最少的是Raptor算法,相同条件下Raptor喷泉码较LT码成功译码所需的译码冗余更少,且编译码耗时更少,是各方面都较为成熟的算法。RaptorQ码更像双刃剑,在追求性能极致的同时,编译码复杂度牺牲最大。
由于在信道删除的情况下,译码端需要接收K个编码符号和额外的译码冗余(修复符号)才能成功解码,为进一步验证RaptorQ码的性能,使用3种算法分别进行删除概率为0.1、0.3、0.5,码长为32、512、1024的仿真试验;设置译码端收到的译码冗余从0开始逐渐增加,直到译码端收到K个编码符号加此译码冗余后,进行105次试验,直至平均误码率小于5×10-5时停止,此时认为排除信道随机删除的不确定影响,喷泉码基本实现无误码。由于删除概率为0.1、0.3和0.5所取得的试验结果一致,选取删除概率为0.1的实验结果如图7~图9所示。

图7 K=32时3种算法所需译码冗余Fig.7 Redundancy of decoding required by three algorithms when K=32

图8 K=512时3种算法所需译码冗余Fig.8 Redundancy of decoding required by three algorithms when K=512

图9 K=1 024时3种算法所需译码冗余Fig.9 Redundancy of decoding required by three algorithms when K=1 024
根据实验结果所示:同等条件LT码需要6~9个译码冗余才能基本实现无误码解码,Raptor码需要2~4个译码,而RaptorQ码仅需1个译码冗余,就能实现极高概率的成功解码。
排除仿真实验的不确定性概率,可以看出,无论是LT码、Raptor码或是RaptorQ码,在信道删除概率为0.1、0.3、0.5以及码长为32、512、1 024条件下成功解码所需的译码冗余几乎相同,说明喷泉码的解码性能与信道删除概率无关,与码长K几乎无关,验证了喷泉码的“独立于信道删除概率特性”。
3 RaptorQ码编译码算法优化
根据仿真及理论分析,RaptorQ喷泉码是性能最好的喷泉码,但也是编译码复杂度最高的喷泉码,在RFC6330设计的RaptorQ喷泉码编译码算法基础上,基于失活解码GE法,提出一个优化版本,针对一部分编解码步骤进行改进。
(1) 固定生成矩阵
第1节详细阐述了RaptorQ码的编译码流程,发现预编码生成矩阵A仅由参数K决定;译码生成矩阵RecA由K以及接收到的编码符号数量决定,RecA矩阵与A矩阵仅在第三层是不同的,前两层完全一致。在实际应用背景下,数据传输的长度K都是提前设置好的,这也就意味着在编译过程中可以提前固定A矩阵以及RecA矩阵的前两层,节省生成时间。
(2) 提前列变换
研究表明,在整个喷泉码编译码算法中,根据生成矩阵和原始信息位求解中间符号的过程是最耗时的操作,将占用整个过程92%~95%的时间,所以优化的重点也聚焦于译码过程,如图10所示。译码过程的第一阶段通过选择标准行和GE法实现,最终形式是在RecA的左上角形成一个单位矩阵。仔细观察生成矩阵的格式,矩阵第一层在G_LDPC,1,G_LDPC,2之间是单位矩阵IS。在选取标准行之前,提前进行列变换,将单位矩阵IS所在列移到生成矩阵的最前方,并将单位矩阵IS固定为前S个标准行,就可以省去S个扫描矩阵行列变换寻找标准行的过程。

图10 提前列变换Fig.10 Advance column transformation
(3) 去稀疏化
为将Uupper子矩阵稀疏化,RFC6330采取将Xi矩阵与其相乘的方法。X矩阵由生成矩阵复制而来,需要与生成矩阵进行同样的标准行选择等复杂计算;其次,采用Xi矩阵稀疏化的过程需要用到矩阵乘法,而且破坏了原生成矩阵左上角单位矩阵的格式,需要在第五阶段再次消元,这些都增加了译码过程的计算量。在第二阶段结束时,生成矩阵中Ulower子矩阵已经化为单位矩阵,所以去掉稀疏化这一步骤,直接用单位矩阵Iu将Uupper子矩阵消元为0矩阵,将生成矩阵直接转化为单位矩阵,将原译码方案的五个阶段也缩减为三个阶段,在一定程度上减少了计算量,优化后的译码流程如图11所示。

图11 优化后的译码流程Fig.11 Optimized decoding process
4 编译码算法优化前后仿真验证
为对比验证优化前后RaptorQ编译码算法的性能变化,进行信道删除概率为0.1、试验次数为105、码长K=128、译码冗余变化的仿真试验,实验结果如图12所示。

图12 优化前后算法误码率对比Fig.12 Comparison of bit error rate before and after optimization
为对比验证优化前后RaptorQ码编译码复杂程度,进行信道删除概率为0.1、译码冗余为0.15、试验次数为105、码长从128~2 048变化的仿真试验。统计3种算法的总异或次数,实验结果如图13所示。

图13 优化前后算法异或次数对比Fig.13 Comparison of XOR times before and after optimization
为对比验证优化前后RaptorQ码编译码复杂程度,进行信道删除概率为0.1、译码冗余为0.15、试验次数为105、码长从128~2 048变化的仿真试验。统计3种算法的平均编解码时长,实验结果如图14所示。

图14 优化前后算法编译码时间对比Fig.14 Comparison of encoding and decoding time before and after algorithm optimization
图12实验结果表明,优化前后RaptorQ码在译码冗余相同时,系统误码率基本一致,排除信道删除的不确定性影响,说明优化后RaptorQ码没有影响原RaptorQ码的解码性能;由图13、图14得知,优化后的RaptorQ编译码流程中的异或运算次数有所减少,同等条件下优化后RaptorQ码所需的编译码时间相比原编译码耗时减少,其编译码复杂程度得到了一定程度的优化。不过将4种算法编译码耗时进行对比,发现即使优化后,RaptorQ码的耗时仍大于Raptor码,其编译码算法仍存在改进的空间。在实际应用中,可根据系统对性能和编译码复杂度的需求选择合适的算法。
5 结 论
针对RaptorQ喷泉码性能和编译码复杂度的评估不够全面清晰的问题,本文在RaptorQ的编译码算法层面,通过理论论证和仿真对比的方式对RaptorQ喷泉码进行全面分析,并针对RaptorQ码编译码复杂度过高这一弊端,以RFC6330所设计的RaptorQ码编译码算法为基础,通过固定生成矩阵、提前列变换和去稀疏化,提出一种RaptorQ码编译码算法的优化版本。通过仿真试验得知,该优化版本在保持原有RaptorQ喷泉码性能的基础上,简化了编译码复杂度,减少了算法中重要运算的计算量,降低了系统处理时间,其有效性和可行性得到了验证。
