基于EM-VB的分布式接收运动目标直接符号检测方法

张 凯, 田 瑶

(1. 中国人民解放军63891部队, 河南 洛阳 471003; 2. 中国人民解放军96862部队, 河南 洛阳 471000)

0 引 言

以提取信息符号为目的,经典组阵接收广泛采用参数差异估计、信号校准合成以及符号检测的逐级处理结构,主要包括符号合成和基带合成两种典型技术方案[1-4],其在不改变现有设备状态条件下,在射频系统和解调单元之间加入合成处理环节,将多路低信噪比信号合成为一路高信噪比信号进行处理,以提升系统性能。在进行合成之前,需要首先对信号进行校准,以保证独立接收信号在时间、频率和相位上保持同步,核心问题是信号间参数差异估计和信号校准,典型做法包括固定参考类方法[5]和多路联合处理方法[6-7]。

现有信号参数差异估计方法主要利用信号间相关性对不同观测站信号时延差异和相位差异进行估计,在诸如小天线组阵、非合作接收、短突发信号处理等应用场合,不同支路信号间的相关性大大减弱,直接影响信号校准精度。在传统合成处理架构下,对存在较大参数差异的观测信号进行合并,容易造成无法恢复的信息丢失,降低系统性能。有别于传统的先合成后解调的解耦处理方案,直接利用多个独立观测站信号进行信息符号的提取,通过有效利用信号接收处理不同环节之间以及多个观测信号之间的关联性进行联合寻优,能够获得更优的系统性能。对此,文献[8]和文献[9]分别给出了基于前向迭代处理的定时同步和载波同步方法。文献[10]和文献[11]则分析了基于频偏和信道参数联合估计的方法。文献[12]进一步给出了载波频偏、信道参数和信息符号的联合求解方法。上述方法将接收处理划分为多个阶段进行综合考虑,以获得性能提升。近年来基于深度神经网络的方法受到广泛关注,文献[13]和文献[14]针对正交频分复用(orthogonal frequency division multiplexing, OFDM)系统的特定应用,分别研究了基于深度神经网络的接收机结构。文献[15-18]则进一步研究了更加通用的深度学习接收机模型,使用深度神经网络代替传统接收机从接收信号中恢复信息比特流。然而上述方法主要针对单个观测站接收系统模型,对于多站分布式接收,文献[19]提出了一种针对分布式接收信号相位偏移和时延的联合处理方法,但主要针对同频非同源信号的参数估计和符号检测的具体应用。文献[20]给出了多天线接收中符号检测、定时参数估计和相位校准的联合处理结构,但其未考虑不同接收信号的质量差异,且主要针对目标和观测站均静止或理想载波同步应用场景,对于实际运动目标或存在收发机频率扰动条件下的处理依然依赖于单路载波同步,实际应用受限。

本文在现有研究基础上,提出了针对未同步运动目标的多天线接收直接符号检测方法。首先基于最大似然准则建立了多天线联合接收直接符号检测求解模型,针对模型中多组未知参数的联合优化问题,理论推导了各未知参数的变分分布,通过泰勒级数展开和数值积分近似方法给出了所有待估参数的闭式解,避免了网格搜索带来的计算量负担。

1 信号模型与问题描述

采用L个独立观测站对同一目标信号进行接收,观测站和目标辐射源均处于运动状态,第l个观测站的等效基带接收信号可表示为

xl(t)=hls(t-τl)ej2πΔfl(t-τl)+vl(t), 1≤l≤L

(1)

基于式(1)的信号模型,传统方法采用参数差异估计、信号合成以及符号检测的逐级处理结构,主要包括符号合成和基带合成两种典型方案,二者结构分别如图1和图2所示。在进行合成之前,首先需要对信号进行校准,以保证独立接收信号在时间、频率和相位上保持近似同步。在诸如小天线组阵、非合作接收、短突发信号处理等应用场合,信号间相关性将大大减弱,合成处理将使独立观测信号信息受到无法恢复的损失,影响系统性能,利用多路观测信号直接进行符号信息的提取具有更优的性能。

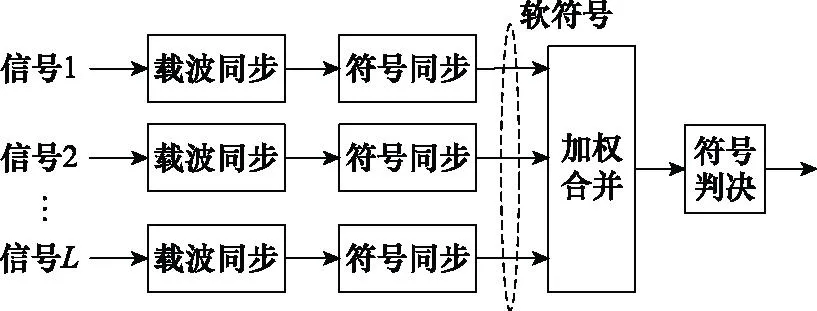
图1 符号合成方案结构示意图Fig.1 Structure schematic diagram of symbol stream combining scheme

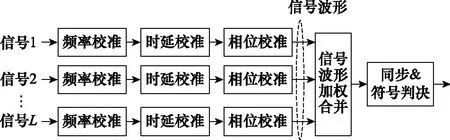
图2 基带合成方案结构示意图Fig.2 Structure schematic diagram of baseband combining scheme

在信道参数已知条件下,对接收信号xl(t)进行匹配滤波后,在t=nTs+τl处进行采样,即可获得待判决的软符号序列,即:

xl,n(τl)=xl(t)|t=nTs+τl=
hlanej2πΔ flnTs+vl,n, 1≤l≤L; 1≤n≤N

(2)

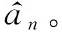
当信道参数未知时,则需要对信道参数和符号序列进行联合求解。令X=[x1,x2,…,xL]为L个观测站采样信号的集合,对应第l个列矢量为xl=[xl,1(τl),xl,2(τl),…,xl,N(τl)]T,a=[a1,a2,…,aN]T为发送符号序列组成的矢量,则多维观测信号X关于待估符号序列a的似然函数可表示为

(3)

式中:βl表示对应噪声序列vl,n的精度参数,为方差的倒数;Dl=diag[ej2πΔflTs,ej2πΔfl2Ts,…,ej2πΔflNTs]为对角阵,对角线元素取决于载波频率偏移Δfl。

基于最大似然准则,最优估计为

(4)

式中:Θ={τ,Δf,h,β}为未知信道参数的集合,Δf=[Δf1,Δf2,…,ΔfL]T,τ=[τ1,τ2,…,τL]T,β=[β1,β2,…,βL]T,h=[h1,h2,…,hL]T。

式(4)优化问题难以直接进行求解,本文借助期望最大化(expectation-maximization, EM)算法对其进行近似求解。以提取信息符号序列a为目标,未知信道参数Θ可视为缺失数据集,观测信号样本X和Θ共同构成完备数据集,则在EM算法框架下,在获得第i次符号序列检测结果ai的基础上,对数似然函数lnp(X,Θ|ai)的条件期望可表示为

Q(a,ai)=EΘ|X,ai[lnp(X,Θ|a)]=

(5)

忽略与a无关的项,式(5)可近似为

Q(a,ai)∝

(6)

式中:R[·]表示取实部运算。对式(6)最大化即可求得新的软符号序列估计式为

(7)

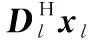
从上面分析可以看出,信息符号的提取依赖于联合条件后验分布p(Θ|X,ai),该后验分布为多组不同类型未知参数的集合,难以直接获得解析解,典型做法为蒙特卡罗和变分贝叶斯(variational Bayesian, VB)方法。蒙特卡罗方法需要大量的观测样本,这也意味着更长的观测时间,容易造成信道参数发生改变。为兼顾复杂度和估计的准确性,本文选用VB对该问题进行处理。

2 联合条件后验概率分布推导及近似处理方法

2.1 VB推导

在给定观测样本X和ai的条件下,本文使用变分分布q(Θ)替代p(Θ|X,ai)进行近似估计,在借助平均场理论对未知参数进行分解的基础上,VB采用迭代处理方式对各参数变分分布进行联合求解[21],估计式为

(8)

式中:θk为Θ的子集,θ1∪θ2∪…∪θK=Θ,且θk∩θj(k≠j)为空集;Θ-θk表示Θ中除θk外元素的集合,C为常数。该估计式中p(X,Θ|si)为p(X|Θ,si)与p(Θ)的乘积,p(X|Θ,si)为多维复高斯分布,通过对各未知参数进行合理先验假设,即可利用式(1)求得其各自变分分布。

在多观测站独立接收系统模型下,可假设各信道系数相互独立,且均服从零均值复高斯分布,从而可令p(h|α)=

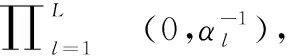
q(hl)∝

CN(μl,Σl)

(9)

式中:μl和Σl的表达式分别为

(10)

(11)

令αl和βl均服从Gamma分布,p(βl|al,cl)=G(al,cl),p(αl|ρl,δl)=G(ρl,δl),则有:

(12)

式中:

4．休闲时间“自由化”。网络方便人们利用点滴时间，在日常工作、学习之余，冲破时间和空间的限制进行休闲活动。“鼠标一点”就可以在网络平台自由、平等选择休闲时间，进行各类休闲活动，突破现实休闲中的种种限制性因素，改变传统某些休闲项目被动、被支配、被监控的状态，它使人们更能切实做到解除体力上的疲劳，获得精神上的慰藉，更为重要的是在网络空间里人们更容易达到休闲的状态，实现工作、学习与休闲无明显界限的和谐理想状态。

(13)

对应βl的期望为

(14)

同理:

(15)

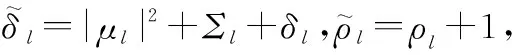
(16)

在残余频偏Δfl先验信息未知的条件下,采用贝叶斯估计的普遍做法[22-24],可令其在取值区间服从先验等概的均匀分布,称为无意义先验,以避免人为错误对估计结果的影响,则有:

(17)

从而有:

(18)

同理,可令τl在取值区间内服从均匀分布,则有:

(19)

从而有:

(20)

2.2 近似解析闭式解

由上述推导结果可以看出,无法直接利用变分分布获得残余频偏Δfl和传输时延τl的闭式解,直接利用式(18)和式(20)进行求解通常需要借助网格搜索。估计精度与网格分辨率密切相关,较高的分辨率意味着庞大的运算复杂度。为此,本节进一步给出其近似形式的闭式解。

(21)

将其代入式(18),容易得到残余频偏近似估计式为

(22)

式中:I[·]表示取虚部运算。

对于传输时延τl,求解过程需要利用q(τl)计算xl,n(τl)关于未知时延的积分,实际上无需获取时延参数的解析解。借鉴文献[26]的思路,可将连续变量积分转化为离散求和问题,即:

(23)

式中:D为离散化时间间隔,求和项∑mql(mD)xl,n(mD)D可视为观测站输出信号波形以D为间隔进行过采样后,对不同子序列进行加权合并,权值则由不同子序列对应时延参数变分分布q(τl)决定。

将上述参数估计结果代入式(7)可得

(24)

2.3 算法流程总结

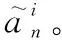
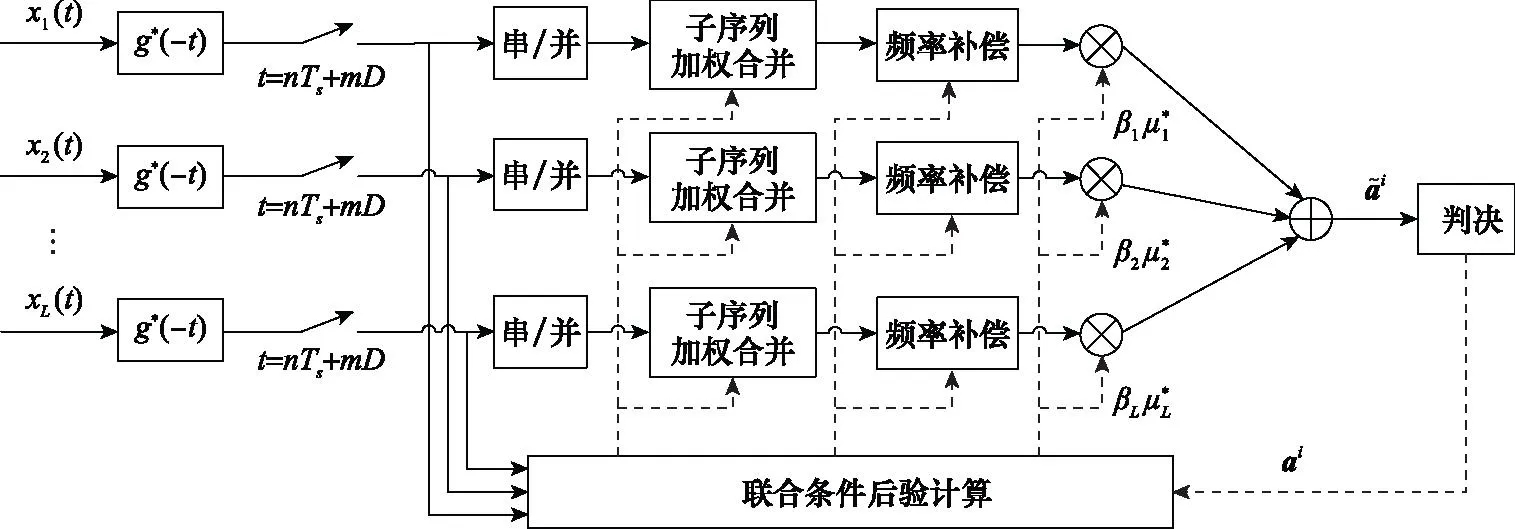
图3 算法流程示意图Fig.3 Schematic diagram of algorithm flow

ai+1←arg max[Q(a,ai)]=

(25)

VB迭代则实现了多组未知参数的联合估计,即:

Θ←arg max[p(Θ|X,ai)]

(26)

EM算法和VB方法的收敛特性分别在文献[27]、文献[28-29]中已有详细的分析,本文在此不再赘述,在第3节结合仿真对其收敛性进行说明。

上述算法的核心为基于VB的多参数联合估计,其利用了信号接收处理不同阶段的关联性,采用迭代重估的思路,借助不同参数估计过程以及参数估计与符号检测之间的相互促进作用,进行联合处理,能够获得比传统解耦处理更优的系统性能。该迭代处理算法性能容易受到初始条件、信号间参数差异及残余频偏大小的影响。在处理过程中,需注意以下几点:

(1) 初始值的选取。

由上文的分析可知,联合条件后验概率计算依赖于符号序列初始检测结果a0,实际在没有导频序列的条件下,可以使用经典合成处理方法的符号检测结果作为初始值,以进行迭代。

(2) 残余频偏Δfl的限定

在式(21)基于泰勒级数展开的近似求解中,需要将残余频偏限定在较小的范围内。残余频偏越小,近似误差也越小。实际接收信号残余频偏主要来源于由目标与观测站相对运动引起的多普勒频率偏移,以及由发射机和接收机之间频率扰动引起的频率误差。上述两种误差难以预先获知,在实际处理过程中,可以使用已有的载波同步技术对各观测信号进行载波频率估计和载波恢复,将载波频率偏移Δfl控制在较小的范围内。

(3) 时延参数积分区间及离散化间隔的选取

根据文献[26]的分析,针对时延参数积分区间的选取,从定时同步角度考虑,τl的取值范围不大于一个符号间隔Ts。而在本文信号模型中,τl表示信号传输时延,通常可以覆盖几十甚至上百个符号周期。在实际处理过程中,不同观测站信号传输时延主要取决于各观测站与目标之间的空间位置关系,较大的时延差异可利用观测站位置关系进行粗补偿,在此基础上可以进一步利用多个观测站接收信号之间相关性对剩余时延差异进行估计和补偿。根据文献[20]的分析,采用根升余弦成型脉冲的信号时,不同观测信号相关函数峰值附近较为平坦,难以直接利用相关函数获取精确的时延差异估计结果,但当时延差异大于半个符号周期后,信号间相关性将大大减弱,可以很容易地将信号间时延差异控制在一个符号周期以内。因此,在实际处理过程中可将积分运算区间设定为0～2Ts。另外,采用式(23)的数值积分方法,通常离散化间隔取值越小越好,这同时意味着较高的计算复杂度。根据文献[26],通常取1/4个符号周期,即可满足实际需求。

3 算法仿真

本节通过仿真对所提算法性能进行分析,并与相关方法进行对比。目标信号采用符号速率为1 MBd的正交相移键控(quadrature phase shift keying, QPSK)调制信号,发射机和接收机的根升余弦成型脉冲滚降系数均为0.25,接收端的采样率为4 Msps,不同支路信道系数独立同分布,服从零均值复高斯分布,且不同观测站处加性噪声平均功率相同,观测信号残余频偏在-1～1 kHz内独立生成。采样信号数据段长度为128个符号周期。

3.1 仿真1:收敛特性分析

以权值估计归一化均方根误差(normalized relative mean squre error,NRMSE)为指标对所提算法收敛性进行说明。由第2节分析可知,各观测站加权合并权值估计式为

(27)

NRMSE的计算式为

(28)

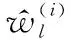
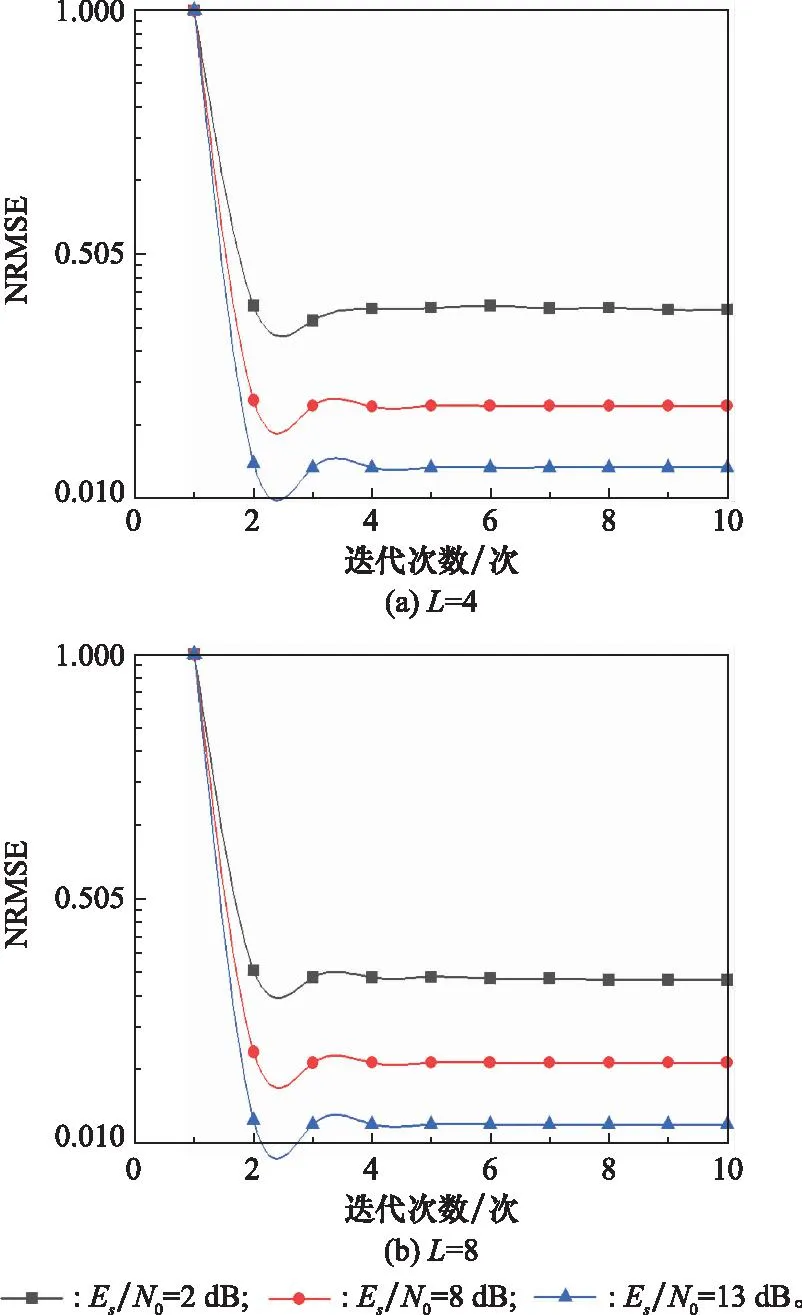
图4 不同观测站数目、不同信噪比下的算法收敛特性曲线Fig.4 Algorithm convergence curves with different number of observation stations and different signal-to-noise ratio

3.2 仿真2:不同信噪比下算法性能分析

图5所示为所提算法与典型合成处理结构的稳态性能对比。图中纵坐标为系统平均误码率(symbol error rate, SER),横坐标为观测站接收信号平均信噪比Es/N0。分别使用符号合成(图中标注为“SymCom&Sync”)、基带合成(图中标注为“BandCom&Sync”)和信道参数已知条件下理想SER曲线(图中标注为“Ideal”)作为对比。在“Sym-Com&Sync”方法中,各观测站信号依次完成载波同步[30]和符号同步[31],得到软符号序列,然后对各软符号序列进行加权合并[32];在“BandCom&Sync”方法中,同样需要首先对各观测站信号进行载波同步[30],然后对同步后的信号波形进行时延和相位校准[6],计算加权合并权值,对多个观测过采样信号波形进行加权合并,并对合成信号进行定时恢复,以得到信息符号序列。

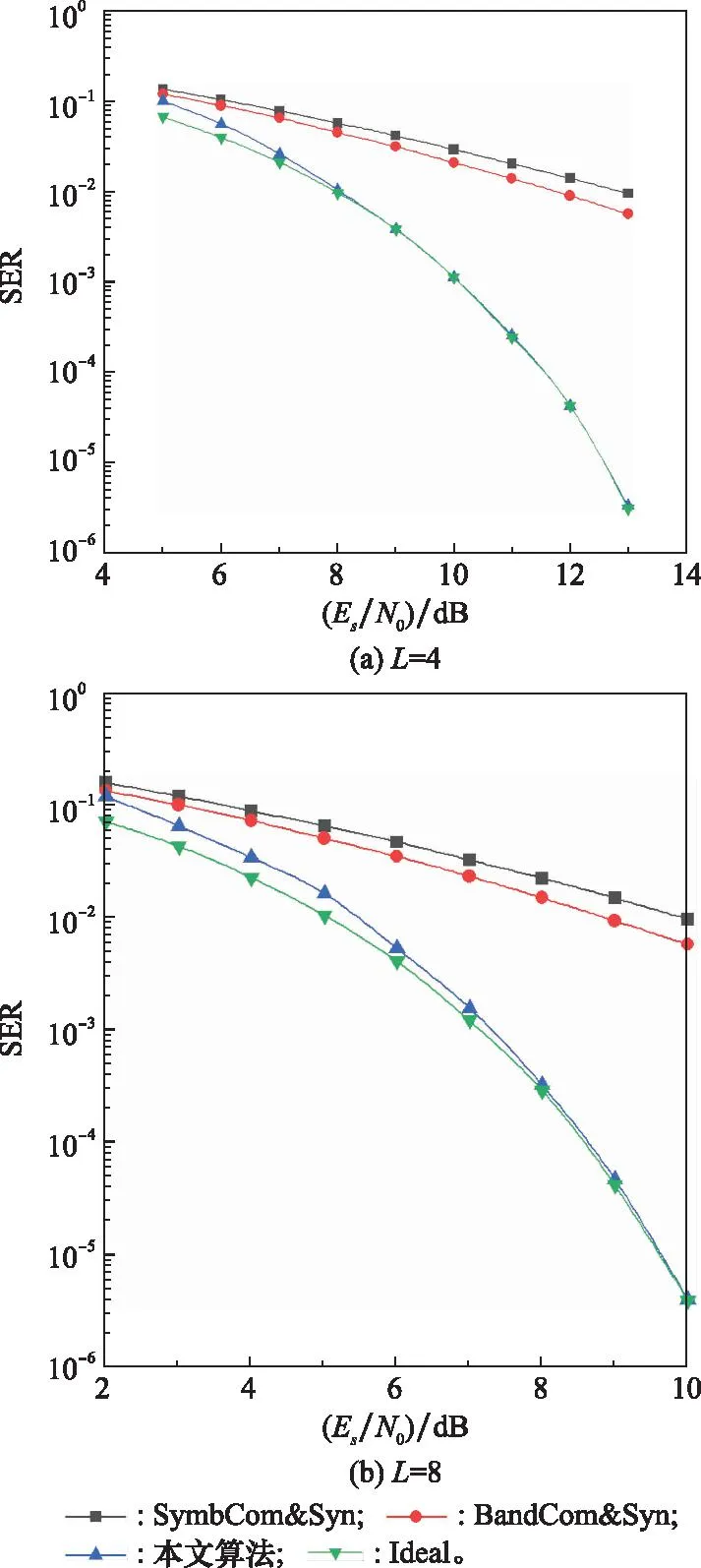
图5 所提算法与典型合成处理结构的性能对比Fig.5 Performance comparison of the proposed algorithm with typical combining structures

从对比结果可以看出,所提联合处理方法性能明显优于传统合成处理方法,且在高信噪比区域体现更加明显。传统合成处理结构采用开环的前向处理结构,依次完成参数差异估计、信号校准/同步、信号合成以及符号检测,上述不同处理阶段实际上是相互关联的,符号检测易受到前端同步参数估计、信号校准等结果的影响。本文算法采用基于迭代重估的闭环判决反馈结构,利用多个参数估计以及符号检测与参数估计之间的相关促进作用进行联合寻优,获得了比传统解耦处理更优的系统性能。

以载波频偏估计为例,图6给出了本文所提算法和文献[30]非数据辅助载波频偏估计方法(图中标注为“NdafreqEst”)的性能对比,图中纵坐标为频偏估计均方根误差(relative mean squre error, RMSE),横坐标为观测信号平均信噪比Es/N0。文献[30]方法为单路估计结果,本文算法观测站数目分别为2、4和8。从图6可以看出,在本文联合处理框架下,载波频偏估计性能明显更优,且估计精度随着接收单元数目的增加而有所提升。

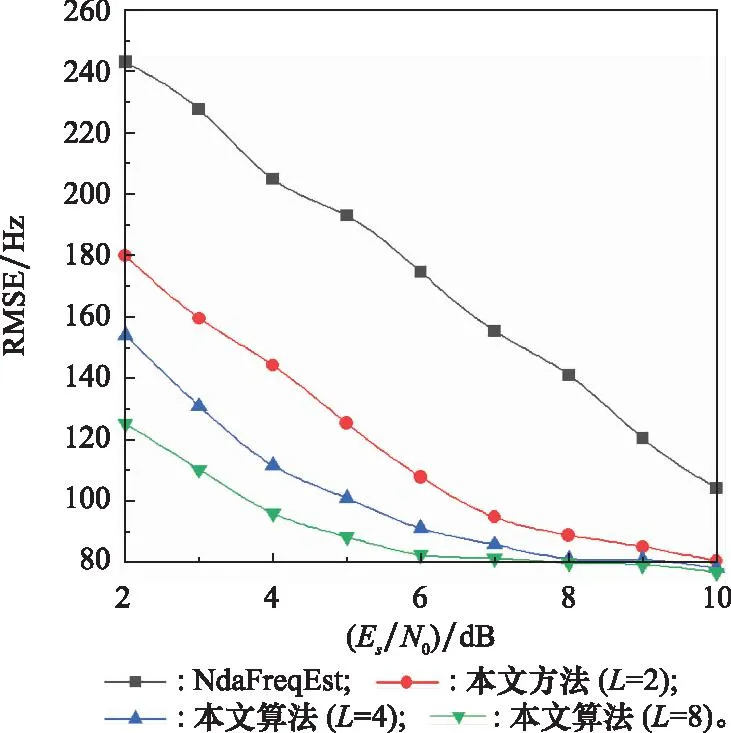
图6 载波频偏估计性能对比Fig.6 Performance comparison of carrier frequency offset estimation

图7所示为所提算法与文献[20](图中标注为“FreqSyn&Shen”)联合处理结构的性能对比。文献[20]仅考虑了多天线信号的时延和相位联合校准问题。在仿真中,首先对各观测站信号进行载波同步和载波恢复[30],然后采用文献[20]方法对载波恢复后的信号进行时延和相位校准,并使用改进二阶、四阶矩信噪比估计方法[32]计算各自加权合并权值,对校准后的信号进行加权合并,最后对合并后软符号序列进行判决得到符号检测结果。从结果可以看出,在相同条件下,所提算法SER性能优于“FreqSyn&Shen”方法,且该优势在观测站数目较多时体现得更加明显。文献[20]方法只考虑了传输时延和载波相位的联合估计,未考虑信号间的质量差异,也没有考虑由目标与观测站之间相对运动、收发机频率扰动等引起的载波频率偏移、载波频偏,以及权值估计均是利用单个观测信号进行,而本文算法则在统一框架下实现联合估计,具有更优的系统性能。

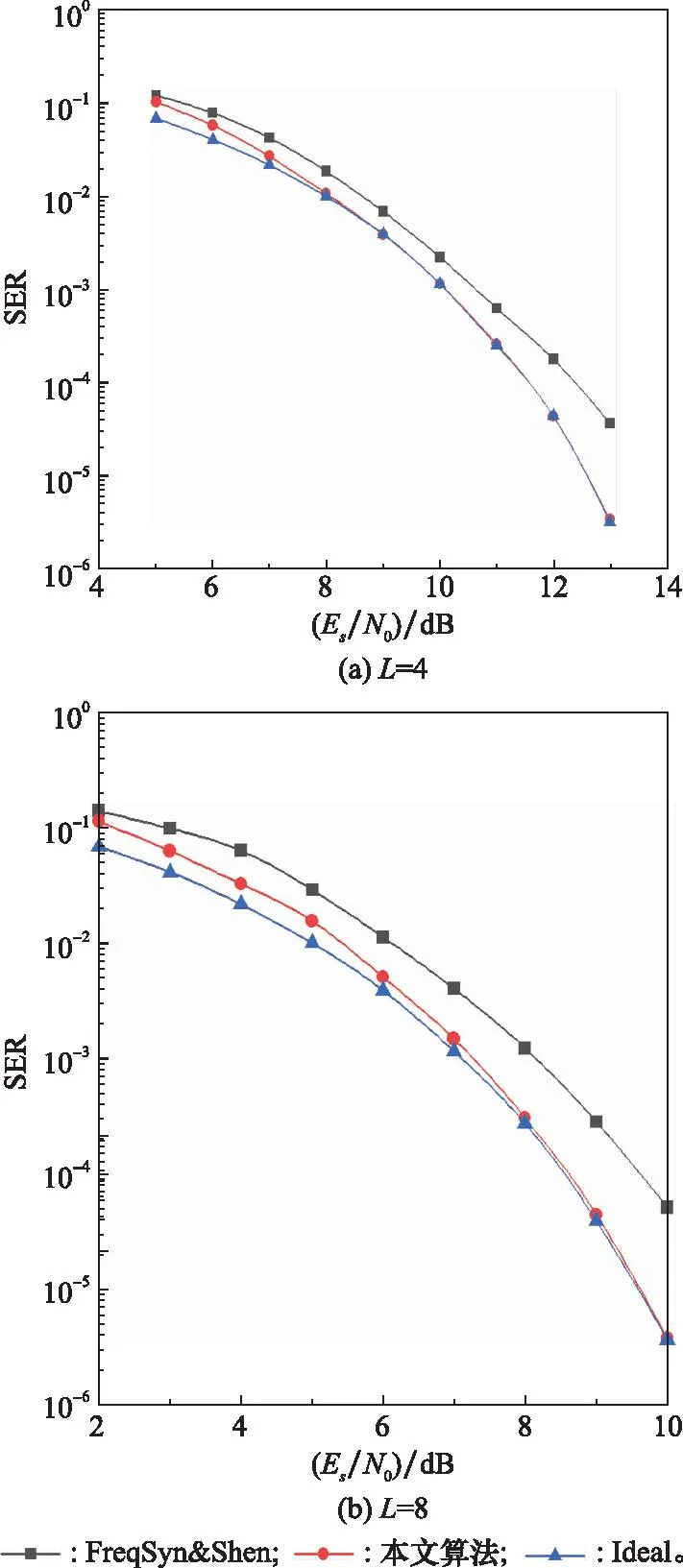
图7 与现有联合处理方法的性能对比Fig.7 Performance comparison with current joing processing methods

3.3 仿真3:不同观测量下算法性能分析

图8所示为不同观测信号长度下,本文算法与Sym-Com&Sync方法、BandCom&Sync方法及FreqSyn&Shen方法的SER性能对比,图中纵坐标为系统平均SER,横坐标为观测信号长度,接收信号平均信噪比Es/N0设为6 dB,接收单元数目为8。从结果可以看出,基于符号流合成的SymCom&Sync方法性能最差,在小样本点(观测信号长度较短)情况下,BandCom&Sync方法与FreqSyn&Shen方法性能接近,但随着观测信号长度的增加,FreqSyn&Shen方法优于BandCom&Sync方法,本文算法SER性能则明显优于其他3种方法,能够获得最优的系统性能。

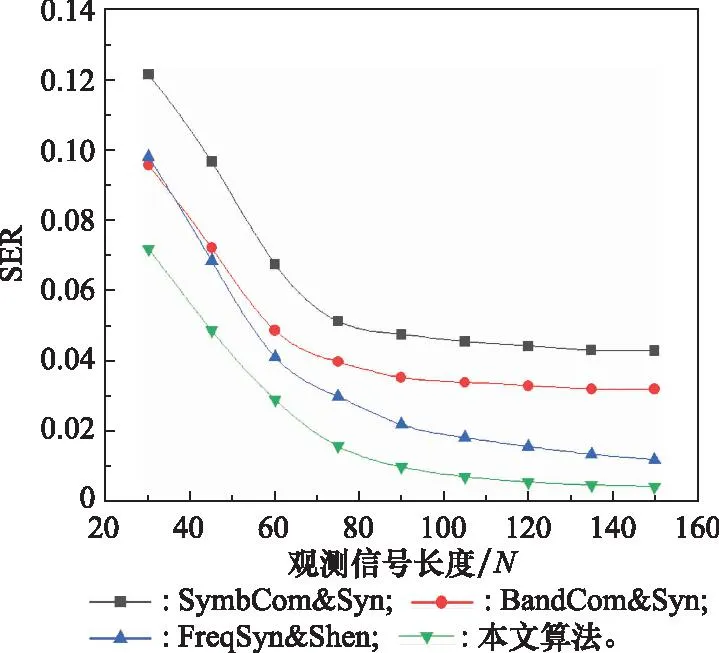
图8 不同观测信号长度下SER性能对比Fig.8 SER performance comparison with different observation signal lengths

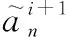
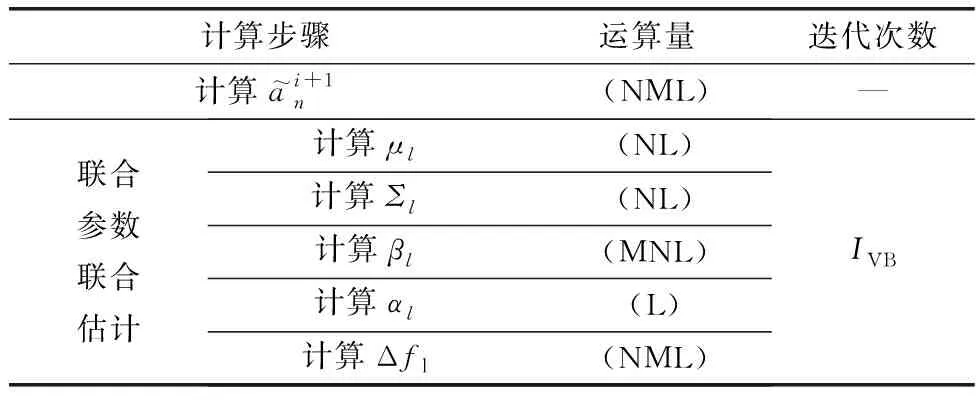
表1 算法运算量分析Table 1 Algorithm complexity analysis

4 结 论

本文提出了一种基于EM-VB的分布式接收运动目标直接符号检测方法,采用迭代重估的闭环判决反馈结构,借助接收处理过程不同阶段的相互促进作用进行联合寻优,获得更优的系统性能。本文主要针对独立信道模型下的处理方法进行了研究。在实际中,当观测站距离较近或存在相关衰落时,不同信道系数将不完全独立。此外,受大气背景噪声和可能存在近场辐射源的影响,在某些环境下各接收信号加性噪声也可能存在一定相关性,对于该非独立信道模型下的处理方法,后续将进行进一步分析研究。