基于波束补偿的成像增强算法研究
2024-03-27宋少秋邢世其汪俊澎李永祯
宋少秋, 邢世其, 汪俊澎, 李永祯, 庞 礴
(国防科技大学电子科技学院电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410073)
0 引 言
合成孔径雷达(synthetic aperture radar, SAR)是一种具有全天时、全天候和高分辨成像功能的雷达[1-4],其被广泛应用于地理遥感探测领域。其中,毫米波近场高分辨率SAR成像是近年来SAR成像技术的研究热点之一,其在机场安检、医疗诊断、自动驾驶、深空探测、车载平台警戒、军事侦察等诸多领域中发挥着重要的作用[5-11]。毫米波作为一种30~300 GHz的电磁波,其波长为1~10 mm,介于微波与光学之间,具有兼顾二者特性的特点[5]。与低频段的微波相比,毫米波段目标的雷达散射截面(radar cross section, RCS)更为敏感,可实现厘米乃至毫米级的高分辨率成像;与光学相比,毫米波具有强穿透性,可穿透如陶瓷、木板、衣物、雨滴等光学不透明材料,并具有对人体皮肤无电离辐射等优点。
毫米波近场成像技术最早提出于20世纪70年代,随着半个多世纪的发展,其在算法研究和实际应用中取得了较大的进展。在国外,美国西北太平洋国家实验室(Pacific northwest national laboratory, PNNL)研制了首台近场毫米波成像系统[12]。Yanik等[3]研究开发的稀疏多输入多输出(multi-input multi-output, MIMO)-SAR毫米波成像系统,可实现任意天线阵列下的成像。新加坡国立大学电气与计算机工程系的Tan等[13-15]研究了用于近场三维成像的快速成像算法研究。在国内,Chen等[16-17]提出了一种近场非均匀 MIMO-SAR体制下基于衰减补偿的快速成像算法,在保证快速成像的前提下有效降低信号传播衰减对成像质量造成的损失。Liu等[18-20]对近场毫米波非视距高分辨率成像也展开了相应研究。与此同时,傲酷雷达、承泰科技、华为科技等企业也对车载毫米波成像展开了系统性研究。
近场毫米波雷达的主要成像算法基于距离徙动算法(range migration algorithm, RMA)[21-27]和后向投影算法(back projection algorithm, BPA)[28-30]。其中,RMA是一种频域成像算法,要求雷达阵列结构为均匀阵列,通过对回波信号进行快速傅里叶变换(fast Fourier transform, FFT),并根据电磁波传播的波动方程理论,将球面电磁波近似分解成一系列平面电磁波的叠加,从而实现了对目标的高分辨率成像聚焦[12],适用范围受限。BPA是一种时域成像算法,可以在任意的天线阵列配置下实现高分辨率成像,这使其成为该领域的研究热点。但传统BPA需要将所有方位向数据相干积累,导致了计算负荷很高,且在实际成像场景中,自然电磁现象、人为电磁辐射、强散射体形成的复杂电磁环境会严重影响近场雷达成像,其产生的旁瓣泄漏、散斑、相干瓣、多次复杂散射和叠影遮挡等现象会存在于目标的局部或整体之上,从而影响成像质量。
针对上述问题,本文提出了一种基于后向投影的成像增强技术,实验结果表明,通过提前生成自适应能量衰减系数矩阵,对目标回波中杂波能量进行衰减,可有效降低周围复杂电磁环境对成像过程的不良影响,从而实现高分辨率三维成像。
本文研究主要分为以下3个部分:第1节分析回顾近场BPA成像与回波模型;第2节介绍BPA成像优化的过程,并给出了自适应回波衰减系数矩阵;第3节通过实测数据进行分析,对比3种成像算法的优劣。
1 成像算法
单基站SAR的等效几何模型如图1所示,以坐标O(0,0,0)为圆心建立笛卡尔直角坐标系,其中雷达以Z形轨迹进行扫描,其均匀等效阵列面上的子阵元坐标为(xi,yi,0),待测目标与阵列面平行,设待测目标上任意一点坐标为(xm,ym,z0)。当雷达发射信号为线性调频连续波时,雷达的回波信号可表示为

图1 SAR成像几何模型Fig.1 SAR imaging geometry model
(1)
式中:tr和ta为雷达快时间和慢时间;fc为雷达的信号载频;Tp为信号脉宽;B为雷达信号带宽;Kr=B/Tp为距离向调频斜率;R为阵列子阵元与待测目标上任意一点的等效距离;τ=2R/c为回波时延。在此,R运用的等效相位模型可表示为
(2)
对回波信号进行去斜,将回波信号与发射信号进行共轭相乘,则基带信号[2]可表示为
(3)
将式(3)进行FFT可得
(4)
式中:fb=Krτ是差频。进一步,将待测目标所在平面网格化,定义成像网格Pjk=(xj,yk,z0),j=1,2,…,m,k=1,2,…,n,其中m,n为成像网格规模大小,则回波时延可表示为
(5)

(6)
由此,可得每个阵列子阵元对整个成像网格的距离向聚焦,遍历所有的阵列子阵元,即可实现方位向聚焦,从而成像。
(7)
2 基于后向投影的成像增强方法
与传统的BPA不同,本文对成像过程中能量的相干积累考虑了衰减补偿,利用雷达天线方向图波束实现自适应能量衰减校准。雷达均匀阵列阵元和归一化天线方向图函数如图2所示,可表示为

图2 雷达均匀阵列阵元和天线方向图Fig.2 Diagram of array elements of radar uniform array and antenna orientation
(8)

在仿真参数中,波长λ=3.89 mm,θ为电磁波与阵元夹角,阵元间隔d=λ/2,β为恒定相位差,雷达天线阵元N=4。
等效阵列面上的子阵元发射的电磁波以球面波的形式向空间扩散后在成像网格上映射为圆,半径r=R′θ′,R′是子阵元与网格上对应圆心的垂直距离,单位为mm。θ′是天线方向图的瑞利宽度(主瓣峰值到第一零点)所对应的角度[8]。圆内成像网格点与圆心间距如图3所示。将圆内的网格点与基于瑞利宽度界限下的雷达天线方向图离散化后的值一一对应,每一个网格点对应一个能量衰减系数。圆之外的网格点处系数为0,从而得到二维自适应能量衰减系数矩阵Qjk,j=1,2,…,m,k=1,2,…,n。其中,m,n为成像网格规模大小,并对其加窗。自适应能量衰减系数矩阵Qjk如图4所示,其表达式为

图3 成像网格点与圆心间距图Fig.3 Distance between imaging grid point and circle center
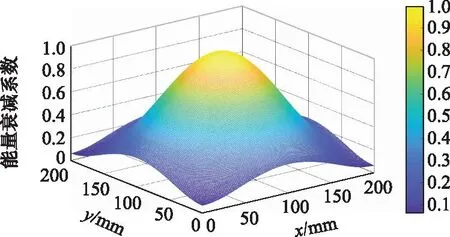
图4 自适应能量衰减系数矩阵图Fig.4 Diagram of adaptive energy decay coefficient matrix
(9)
式(7)经过衰减补偿后,最终成像结果可表示为
(10)
3 实测论证与结果分析
3.1 实验系统和实验方案
为模拟图1中的SAR体制模型并验证所提算法的有效性,本文搭建了一套频率为77 GHz的近场毫米波成像雷达系统。其基本配置由3部分组成:德州仪器公司研发生产的毫米波雷达传感器IWR1843、高性能数据采集卡DCA1000和四川Fuyu公司生产开发的一台高精度三轴轨道。电脑通过串口来控制雷达传感器和导轨的工作,并使用网口获取雷达目标原始回波数据。实测成像场景如图5所示。算法的设计主要包括以下5个步骤,如图6所示。

图5 成像场景图Fig.5 Imaging scene map

图6 本文算法流程Fig.6 Flowchart of the proposed algorithm
步骤 1雷达发射电磁波照射物体获得回波数据,并对回波距离维执行FFT操作,将时域回波信号变为频域回波信号,得到S(fr,ta)。
步骤 2利用雷达系统参数及天线尺寸,仿真天线方向图,将瑞利宽度作为判决标准,形成二维波束图,将其离散化并与成像网格点一一对应,生成二维自适应能量衰减系数矩阵Qjk。
步骤 3计算当前方位点与成像网格上所有点的距离,得到其双程时延。
步骤 4将步骤1中的频域回波进行距离索引、相位校准、衰减补偿,并遍历所有方位点,获得一个等距离切片的二维图像。
步骤 5判断是否有待测物体的其他距离切片,若有,则转到步骤3,对新的距离切片进行二维成像;若无,则将所有切片合并,实现三维图像重构。
本文对上述算法方案进行实测论证。近场毫米波SAR平台通过Z形轨迹进行扫描,毫米波雷达以正侧视模式对剪刀进行成像。毫米波雷达系统参数如表1所示。
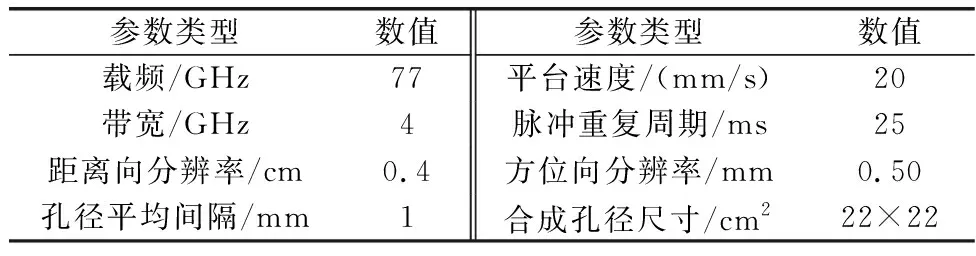
表1 毫米波雷达系统参数表Table 1 Parameters table of millimeter wave radar system
3.2 实测结果及分析
本文用实测数据验证一种基于后向投影下天线方向图波束补偿的成像增强方法(以下简称BPA增强算法)的有效性。BPA、RMA及BPA增强算法对同一组剪刀数据进行成像后的重构示意图分别如图7~图9所示,从图中可以看出,这3种方法都可以对剪刀模型进行恢复重构。

图7 BPA成像重构图Fig.7 BPA imaging reconstruction map
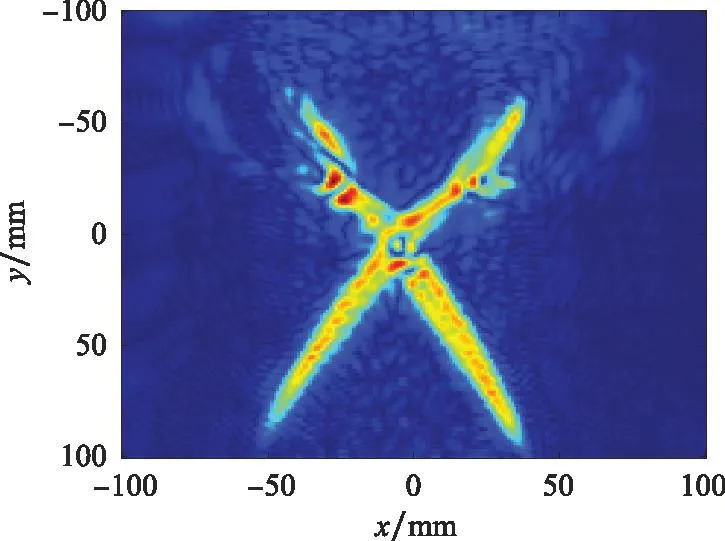
图8 RMA成像重构图Fig.8 RMA imaging reconstruction map

图9 BPA增强成像重构图Fig.9 BPA enhanced imaging reconstruction map
数据采集过程在实验室进行,室内放角反和大量强散射体形成复杂的电磁环境。由图7~图9可以看出,由于BPA的图像质量较差,图像上存在大量的旁瓣且物体细节信息丢失较为严重,背景区域杂波较多;RMA则清晰地还原了图像的整体轮廓和细节,且周围环境杂波较少;相比于前两种算法,本文算法在实现二维图像重构的同时也进一步降低了旁瓣,使成像聚焦效果明显,细节恢复更好。
为定量分析这3种方法下散射点的成像效果,三者在同一方位向下剪刀刃处的像素幅度值如图10所示。从图10可以清晰地看到,BPA得到的待测目标上散射点的主瓣强度有所衰减,且旁瓣强度大约为20~40 dB,而BPA增强算法和RMA得到的目标散射点主瓣强度无明显衰减。对比BPA与RMA,BPA增强算法下的旁瓣强度可衰减到60 dB,且主瓣更窄,旁瓣衰减更快,目标成像聚焦效果更好。
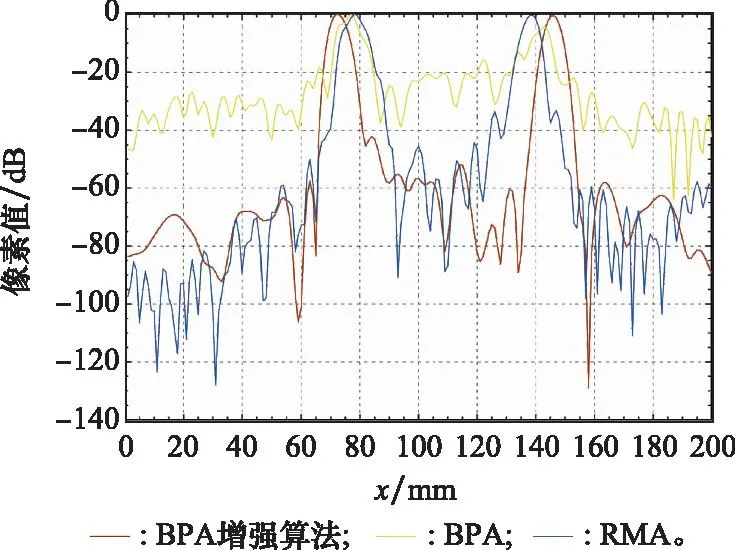
图10 方位向散射点像素幅度Fig.10 Azimuthal scattering point pixel’s amplitude
3.3 三维成像重构
将这3种成像算法得到的图像数据进行自适应滑窗滤波后,实现三维重建[31]。图11为待测物体的光学图像;图12是三维(three dimensional,3D)-BPA成像结果;图13是3D-RMA图像;图14是3D-BPA增强重构图。从图中可以看出,利用BPA得到的图像中剪刀刀刃存在短缺,剪刀把完全缺失,而RMA和本文算法则较为完整地实现了高分辨率三维图像重构,基本恢复了图像原貌。

图11 剪刀光学图Fig.11 Scissors optical diagram

图12 3D-BPA图像Fig.12 3D-BPA image
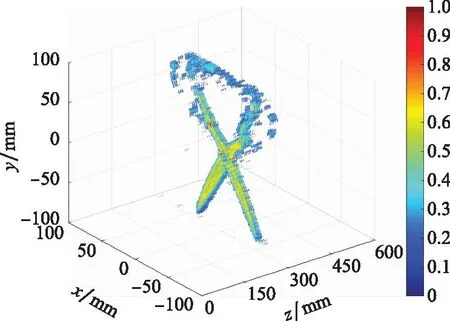
图13 3D-RMA图像Fig.13 3D-RMA image

图14 3D-BPA增强图像Fig.14 3D-BPA enhanced image
由分析结果可知:毫米波雷达发射的电磁波以球面波的形式向空间四周传播,而BPA成像则是将每个子阵元与待测目标上散射点之间的距离通过距离索引得到的幅度信息填充到成像网格单位上。当周围电磁环境较为复杂时,自由空间中其他区域的杂波信息也会相应覆盖到成像网格,使成像物体上目标的弱散射体信息被淹没,从而导致图像细节不清晰。而本文提出的算法能有效抑制周围杂波并降低旁瓣,从而实现成像增强,有效提高了图像质量和成像过程中的鲁棒性。
4 结 论
本文通过优化BPA提出了一种基于天线方向图波束补偿的成像增强技术。该技术通过生成自适应能量衰减系数矩阵,对回波模型进行了幅度衰减补偿,能有效克服复杂环境对成像过程的不良影响,提高图像质量。其次,由于本方法提前生成了能量衰减矩阵,有效降低了BPA成像过程中相干积累的次数,从而提高了成像效率。实验结果表明,该方法的提出可以保证BPA优化后的算法能达到与RMA相同的成像效果,并提高了成像的动态范围,有利于将高质量图像作为输入服务于后续的图像检测识别应用中。
