面向直流受端新型电力系统暂态电压稳定的紧急控制策略

李轻言，林 涛，杜 蕙，付希越，李 君，徐遐龄，李大虎，饶渝泽

（1.交直流智能配电网湖北省工程中心，湖北 武汉 430000；2.武汉大学 电气与自动化学院，湖北 武汉 430072；3.国家电网公司华中分部，湖北 武汉 430077；4.国网湖北省电力有限公司，湖北 武汉 430077）

0 引言

大规模可再生能源发电已成为中国乃至世界实现低碳社会目标的重要举措。在特高压交直流互联电网中，往往通过常规高压直流输电（high voltage direct current，HVDC）实现跨区域远距离输电［1］。直流馈入导致受端电网换流站近区同步发电机为主的动态无功源减少［2］，同时，若受端电网换流站近区存在一定比例的新能源电源出力，则同步机开机将进一步减少，受端电网动态无功平衡将更为紧张［3］。HVDC 落点通常位于受端电网负荷中心附近，当异步电动机作为负荷中心主要负荷时，受端电网，尤其是换流站近区的故障可能会导致持续的电压下降。一般认为，暂态电压失稳与异步电动机转差的持续增加有关［4］，这会导致更多的无功功率消耗，负荷节点电压进一步降低，转差继续增加。这种等效转差无功正反馈过程最终导致暂态电压失稳。

为避免暂态电压失稳，需要在故障发生后进行紧急控制，通常的紧急控制手段包括切机、切负荷等，然而切机不利于电网的恢复，发电机再并网还可能造成冲击，切负荷则存在经济性和可靠性的问题［5］。此外，新一代调相机在动态无功及暂态电压稳定支撑能力上具有突出性能，部分研究考虑提高调相机的励磁电流和强励时间的紧急控制策略以对电网进行无功支撑［6］，但会相应地大幅增加调相机等设备的建设与运维成本。

HVDC 具有毫秒级的响应速度，可以快速对互联电力系统进行有功功率调控［7］。文献［8］以降低直流电流的方式调节直流输送功率，释放换流站电容的无功能力，将直流逆变站作为受端电网大容量动态无功源，在暂态电压失稳为主导的失稳状况下提升受端电网的电压水平。基于此，可以考虑调节直流有功功率来应对直流受端电网的暂态电压稳定问题。然而，文献［8］的不足之处在于采用试探性的方法逐步降低直流电流指令，对电压恢复的控制效果较为缓慢。文献［9］考虑到固定参数的依压限电流控制器（voltage dependent current order limiter，VDCOL）难以适应直流馈入地区电网的运行方式和故障复杂性，提出了一种基于换流母线电压水平的自适应电流控制策略，依据逆变站交流母线电压水平动态改变VDCOL 高电压门槛值，表明在不同情况下动态地控制直流电流能够提高受端电网的暂态电压稳定性，然而如何根据受端电网的运行方式或故障等信息设置高电压门槛值缺乏明确的理论指导。文献［10］通过优化VDCOL 曲线来提升直流系统对受端电网暂态电压恢复的支撑能力，然而该方法属于预防控制方法，优化的VDCOL 曲线难以适用于直流受端电网复杂运行方式下的紧急控制。

直流受端新型电力系统中，新能源电源开机及出力变化导致电网运行方式多变，不同的运行方式下电网的稳定形式有所差别，因此紧急控制策略也有所不同。常规做法为离线生成1 个或多个较为保守的紧急控制策略来应对新型电力系统大量不同运行方式和故障场景，因此控制代价较大。为了降低控制代价，有必要针对具体的运行方式和故障场景在线获取紧急控制方案。

为了解决上述紧急控制策略在线制定在计算效率上的不足，人工智能领域中的深度强化学习（deep reinforcement learning，DRL）方法逐渐进入研究者视野，并应用于电网紧急控制策略的制定。文献［11-12］针对故障后的电压延迟恢复问题，通过对电网状态的实时监测，提出基于DRL 方法制定连续时段内的切负荷策略。为应对大电涌导致的瞬时电网冲击，文献［13］提出基于多Q 学习算法和深度确定性决策梯度（deep deterministic policy gradient，DDPG）的紧急频率控制模型，实现以切负荷为控制手段的紧急控制。然而，以上研究对象均为常规交流电网，并未考虑直流和新能源场站的接入，相应的紧急控制策略也未考虑直流功率调控。此外，以上研究并未考虑电网拓扑结构的变化，若电网拓扑或故障位置发生变化，训练好的基于DRL 的紧急控制模型的有效性需进一步探讨。

图卷积神经网络（graph convolutional network，GCN）是一种能够反映节点之间连接关系的深度学习方法，相较于常规全连接神经网络仅以电网状态信息为输入，GCN 还能兼顾电网拓扑结构信息。文献［14］通过预处理将微电网拓扑图转化为线图，从而基于GCN 实现微电网拓扑状态的辨识。文献［15］利用直流电网节点电压信息，基于GCN 考虑节点之间的拓扑信息，实现节点电压估计。文献［16］为解决故障后的电压延迟恢复问题，提出GCN 改进的深度Q 网络（deep Q network，DQN）算法，用于紧急控制策略的快速制定，然而受制于DQN 算法的神经网络结构，该算法难以适应连续动作空间上的决策。

基于以上考虑，针对直流受端电网暂态电压稳定问题，为高效快速获取紧急控制策略，即直流电流控制方案，并使其适应不同的电网运行方式和故障，尤其是电网拓扑结构的变化，本文基于GCN 对常规深度强化学习模型DDPG 的网络结构进行改造，构建了GCN-DDPG 融合模型，在此基础上，引入双评价网络机制和评价网络与动作网络非同步更新策略以提升算法效果；进一步地，在应用方面，基于GCNDDPG 融合模型构建紧急控制模型并将其下达至安控主站。具体应用时，安控主站将依据电网实际运行方式和故障等信息，对紧急控制策略进行在线量化计算并将其发送至直流控保系统执行。

1 GCN-DDPG融合模型

以电网为研究对象时，传统的神经网络仅以电网状态信息作为输入，忽略了节点间的连接关系，导致部分有用信息遗失，而GCN 除电网状态信息外，还兼顾了电网拓扑结构，考虑的信息更为全面。DDPG 是一种基于价值与基于策略结合的DRL 算法，优势在于能够适用于高维连续的输入与输出［17］，然而，作为基于传统神经网络的DRL 算法，DDPG 模型也忽略了电网拓扑结构，故本章用GCN 替代DDPG 网络结构中的部分全连接网络层，构建了GCN-DDPG融合模型，实现对拓扑结构的感知。

1.1 GCN简介

GCN作为一种直接在图上进行类卷积操作的神经网络，能够直接处理非欧氏数据［18］，其结构如附录A 图A1所示，输入包括n×d（n为节点个数，d为各个节点的特征个数）维特征矩阵X和n×n维邻接矩阵A。在图卷积层中，节点的特征以隐藏特征的形式在图结构中流动。图卷积层的具体运算表达式为：

式中：L为卷积层的总数；Hl为第l层卷积层的输入特征数据，当l=0时，Hl=X；Wl为第l层卷积层的权重矩阵；σ(·)为激活函数。

然而这种传递规则之下，由于节点不存在自连接，邻接矩阵A对角线位置的元素均为0，节点自身信息在特征提取时被忽视。此外，由于邻接矩阵A没有被规范化，在经过多层的矩阵变换后，它和输入特征的幅值差距将越来越大，不利于神经网络的训练。为此，将邻接矩阵A与单位矩阵I相加，从而给每个节点增加了1条自连接，并对邻接矩阵A进行规范化，如式（2）所示。

式中：A′为考虑节点自连接的规范化后的邻接矩阵；D̂为邻接矩阵A的度矩阵。

GCN 以梯度下降的方式对各层的权重矩阵Wl进行更新优化。根据式（1）、（2）的传递规则可知，当输入特征数据H的维数为n×1 时，图卷积前后Hl始终保持n×1 维，与传统全连接神经网络的输入与输出结构相似。因此可以考虑用GCN 替代DRL 神经网络中的部分全连接层，实现DRL 对拓扑信息的感知。基于此，本文提出了GCN-DDPG 融合模型，具体见1.2节。

1.2 GCN-DDPG融合模型网络构建

DDPG 模型网络包括动作网络和评价网络两部分，动作网络用于生成动作，评价网络基于对回报函数的定义生成动作的评价［19］。为了进一步反映电网拓扑结构，本节基于1.1节中的GCN 模型，用GCN 替代DDPG 网络中的部分全连接神经网络层，构建了GCN-DDPG 融合模型，以提升DDPG 模型对拓扑结构的感知，其结构如图1 所示。动作网络的输入为由特征矩阵X表征的节点电压信息和由邻接矩阵A表征的电网拓扑结构，输出为直流电流控制量；评价网络的初始输入与动作网络相同；图卷积层后的第1 个全连接层由卷积层输出和动作网络生成的动作组合而成，输出即为该环境状态下所施加的动作的Q值，用于动作的评价。

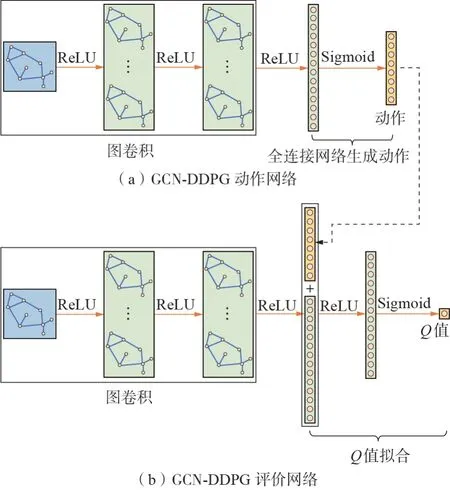
图1 GCN-DDPG融合模型网络结构Fig.1 Network structure of GCN-DDPG integrated model

特征矩阵X用于描述某一时刻下的节点电压，因此节点特征数d为1，GCN-DDPG 融合模型网络的图卷积层和全连接层运算的区别在于是否引入了邻接矩阵，即层间信息传递规则的不同，对于图卷积层，层间信息传递规则具体为：

式中：H和H'分别为层级输入和输出；WGCN为图卷积层权重矩阵；bGCN为图卷积层偏置向量；ReLU（·）为激活函数。

对于全连接层，层间信息传递规则具体为：

式中：WFC和bFC分别为全连接层权重矩阵和偏置向量。

根据式（3）、（4）可知，各层输入与输出均为一维向量，权重矩阵WGCN与偏移向量bGCN也均为一维向量，其维数与输入保持一致。因此，考虑图卷积层参数WGCN和bGCN与全连接层参数WFC和bFC在数据结构上的一致性，本文将以上参数进行协同优化，对于评价网络和动作网络，分别构建参数组θQ和θμ。

由于GCN 结构的引入，GCN-DDPG 融合模型的复杂度提升，导致受噪声影响更加严重，易出现过拟合现象；此外，常规DDPG 模型算法中动作-评论框架采用的Q值估计往往会出现高估偏差的情况，为此引入双评价网络机制，在原评价网络基础上，增加一个相同结构的评价网络，2 个评论网络都用来估计目标Q值，每次更新时都选取较小的Q值，从而减少噪声和高估偏差带来的影响。需要说明的是，这2 个评价网络结构相同，但参数及其更新互不影响，本文将这2 个评价网络分别表示为Q1和Q2，其参数分别为θQ1和θQ2。

常规DDPG 模型算法中评价网络以损失函数最小为目标实现评价网络的优化［19］，GCN-DDPG 融合模型算法基于以上改进，损失函数修改如下：

在训练过程中，为了提高训练的稳定性，目标网络每间隔一段周期通过在线网络更新，记周期为K，更新策略如式（6）所示。

式中：τ为网络更新速率。

模型训练过程中，动作网络进行参数更新时的误差会影响到评价网络对Q值的估计，Q值反过来也是动作网络更新的参照，因此Q值的不稳定会引起训练过程的较大波动。另一方面，由于引入了双评价网络，GCN-DDPG 模型网络参数进一步增加，导致训练复杂度进一步提升。因此训练过程中更容易出现Q值不稳定引发的波动，加大训练结果的不确定性。评价网络稳定后再训练动作网络有利于减少不合理的策略出现，因此本文采用评价网络与动作网络非同步更新策略，评价网络参数更新若干次稳定后再更新一次动作网络参数，一方面避免Q值的不稳定引发的波动，另一方面降低参数更新频率提高训练效率，从而提升算法效果，动作网络更新策略如式（7）所示，对算法的改进详见附录A图A2。

式中：t=1，2，…，T，为动作或状态的时刻，T为控制的最终时刻；∇表示求梯度。

与常规的DDPG 模型相比，GCN-DDPG 融合模型得益于GCN 的引入，实现了对数据连接关系、即拓扑的感知。因此，当应用于电网等具有拓扑连接关系的研究对象时，能够避免对电网连接关系或故障导致的拓扑变化等信息的忽略。

本章提出的GCN-DDPG 融合模型应用于直流受端电网紧急控制策略，即直流电流控制方案的快速求解，得到基于GCN-DDPG 融合模型的紧急控制模型，其过程将在第2章详细阐述。

2 基于GCN-DDPG融合模型的紧急控制模型

面向直流受端电网故障后的暂态电压稳定问题，基于直流逆变站可用作受端电网的紧急无功电源的思想［8］，为实现紧急控制策略，即直流电流控制方案的量化计算，根据文献［20］构建了以直流电流能控制变量，以直流传输能量降低最小为目标，以节点电压等为约束的优化模型，详见附录B。然而基于优化的方法难以适用于大量不同运行方式的紧急控制策略的获取，为此本章将电网作为环境，将直流电流Id作为动作，基于GCN-DDPG 融合模型构建HVDC 受端电网紧急控制模型，以快速获取直流电流控制方案。本文借助电力系统分析综合程序（power system analysis software package，PSASP）构建电网模型，电网模型与基于GCN-DDPG 融合模型的紧急控制模型每0.2 s 进行一次交互：通过故障后暂态过程的时域仿真获取节点电压等电网数据，发送至GCN-DDPG 融合模型，GCN-DDPG 融合模型据此生成动作并作用于电网，依据电网状态的变化对动作进行评价。动作如式（8）所示。

式中：Idt为t时刻的直流电流控制量。依据CIGRE直流标准测试系统，直流电流区间设定为［0.5，1.0］ p.u.［21］。

对于DDPG 模型，其动作与GCN-DDPG 融合模型相同，而状态量方面，由于DDPG 模型采用全连接神经网络，其状态量SDDPG如式（9）所示。

式中：Ut为t时刻电网各个节点的电压向量。

为了反映电网拓扑信息，根据1.1 节的描述，GCN-DDPG 融合模型输入为特征向量X和邻接矩阵A，状态量SGCN-DDPG表示为：

式中：X即为Ut；At为t时刻表征电网拓扑的邻接矩阵；D̂t为At的度矩阵。

依据《电力系统安全稳定计算技术规范》［22］，本文采用如下暂态电压稳定判据：在电力系统受到扰动后的暂态过程中，负荷母线电压能在故障后10 s内恢复到0.8 p.u.以上（记为判据1）。综合考虑稳定性、稳定裕度和稳定控制代价，回报函数rt表达式为：

式中：tf为故障时刻；min(v(t))为时刻t全网电压最低值，通常对应故障位置附近母线电压幅值；at表示时刻t的动作量。在故障后10 s 内，若施加动作后，全网最低节点电压大于等于0.8 p.u.，则表明暂态电压恢复至稳定标准以上，给予正回报，且该电压值越大，回报越大；若最低节点电压仍小于0.8 p.u.，则给予负回报，且该电压值越小，回报越小。若故障10 s后，在施加动作的情况下电网最低节点电压仍小于0.8 p.u.，则给定回报-500，并结束该训练轮次。此外，为满足受端电网功角稳定和频率稳定，若故障后功角差大于180°或稳态频率超出基准频率 ±0.2 Hz（本文算例中直流受端电网为220 kV 电压等级，因此采用此标准）的波动范围时，同理给定回报-500，并结束该训练轮次。

需要说明的是，《南方电网安全稳定计算分析导则》［23］规定的暂态电压稳定判据（记为判据2）如下：故障后暂态过程中系统中枢点母线电压下降持续低于0.75 p.u.的时间不超过1 s，且暂态过程结束后220 kV 及以上电压等级中枢点母线电压不低于0.9 p.u.。判据1 与判据2 在电力系统暂态电压稳定判别方面均得到了广泛应用。本文采用判据1 对电网暂态电压稳定进行约束，若采用判据2 或结合判据1和判据2对电网暂态电压稳定进行约束，则可通过调整式（11）所示的回报函数实现。

GCN-DDPG 融合模型与直流紧急控制结合工作，体现在紧急控制措施的获取及实施方式上。常规做法为离线生成1 个或多个较为保守的紧急控制策略来应对新型电力系统大量不同运行方式和故障场景，因此控制代价较大。为了快速生成紧急控制策略并降低策略的保守性，本文将训练好的基于GCN-DDPG 融合模型的紧急控制模型而非具体的紧急控制策略表下发至安控主站，安控主站将依据电网实际运行方式和故障信息，在线生成相应的紧急控制策略，即直流电流控制方案，并将该方案发送至直流控保系统执行：在直流恒电流控制模式下，将直流电流控制方案作为电流参考值Iref，Iref与VDCOL得到的电流IVDCOL相比较，取较小的值作为最终的电流指令，应用流程如图2 所示。因此，本文所提方法将紧急控制从传统的离线制定在线应用的方式转变为在线制定并执行，实现紧急控制策略的快速生成，提高效率并降低了策略保守性。

图2 紧急控制模型应用流程Fig.2 Application process of emergency control model

3 算例分析

本章以改造的IEEE 14 节点系统为例验证本文所提方法的有效性和优越性，算例系统的结构见附附录C图C1，参数设置见附录C表C1 — C3。

常规紧急控制策略输出为离散控制量，由于DQN 在动作生成方面，其输出的动作指令值为离散值，因此适用于常规紧急控制策略的生成。而本文紧急控制策略输出的直流电流控制指令为连续值，此时DQN 不再适用，因此本文采用DDPG 来满足输出动作为连续值这一要求，而未采用DQN 及其他相关强化学习算法。进一步地，本文将DDPG 模型与GCN 结合，提出了GCN-DDPG 融合模型，实现对电网拓扑结构的表征，因此，本文聚焦GCN-DDPG 融合模型相对DDPG 模型的效果提升，在3.2 节进行了详细分析。

3.1 样本获取

不同的负荷水平及参数、发电机及新能源场站开机及出力情况、故障位置等会影响电网的暂态电压稳定性［24］。因此为了获取大量不同的运行方式来训练基于GCN-DDPG 融合模型的紧急控制模型，调整表C1中的负荷以设置不同的电网整体负荷水平，包括基准负荷水平的80 %、90 %、100 %、110 % 和120 % 这5种负荷水平，每种负荷水平下随机改变各个负荷出力和负荷类型及其比例，并相应调整表C2中的发电机开机情况和出力情况以维持潮流收敛，因此可以认为通过以上调整，电网整体的负荷特性也随之改变；同时调整风电场出力以改变新能源电源渗透水平，风电机组以每4 台机为单位控制机组启停。故障位置考虑线路9-14 的节点14 近端或线路9-10的节点9近端，故障均为三相短路接地故障。此外，断开原始拓扑的1 条线路以考虑不同的电网拓扑，基于以上分析，样本获取的具体方案如附录C表C4所示。

基于表C4 样本获取方案，若样本类型不重复，则将包含400 种可能的组合。在训练阶段按照每种组合等比例随机出现原则，通过PSASP 时域仿真生成4 000个训练样本。需要说明的是，在样本生成过程中，由于发电机出力及负荷等的调整，可能出现潮流不收敛的情况，若潮流不收敛，则舍弃该样本继续生成，直至得到4 000个训练样本。

在测试阶段，同理生成800 个常规测试样本。此外，考虑70 % 和130 % 这2 种负荷水平（均考虑G2不开机），线路2-3 及线路4-5 断开2 种拓扑，故障位置设置为线路9-14 的节点14 近端或线路9-10 的节点9 近端，同理生成400 个泛化测试样本。因此，总训练样本为4 000个，总测试样本为1 200个。

3.2 紧急控制模型训练及测试

本节基于图C1 所示的算例系统，按照3.1 节所述方案生成样本训练基于GCN-DDPG 融合模型的紧急控制模型。为验证其优越性，本节同时训练基于常规DDPG 模型的紧急控制模型作为对比。以上算法均基于python 语言在PyCharm 平台运行，深度学习框架为Tensorflow2.0。计算机硬件配置为32 GB内存Intel Xeon Platinum 8124M CPU，GeForce RTX 3909Ti GPU。

基于GCN-DDPG 融合模型与常规DDPG 模型的紧急控制模型训练过程回报如附录D 图D1 所示。由图可见：GCN-DDPG 融合模型各个训练轮次的总回报呈现逐渐上升后稳定的趋势，基于式（11）对回报函数的定义可知，在训练初期，存在施加动作后仍然暂态电压失稳的情况，训练后期，各个轮次的回报维持在-100 左右，可见后期对直流电流的控制能够实现直流受端电网暂态电压稳定；常规DDPG 模型训练后期各个轮次的回报维持在-150 左右。基于GCN-DDPG 融合模型的紧急控制模型具有更快的收敛速度，训练过程波动更小，一方面，这得益于动作与评价网络非同步的更新策略，评价网络稳定后再训练动作网络，更新其参数，从而一定程度上避免了不合理策略的出现，提升了训练效率；另一方面，双评价网络的引入减轻了高估偏差和噪声的影响，使训练过程更加稳定。

基于GCN-DDPG 融合模型与常规DDPG 模型的紧急控制模型测试过程回报如附录D 图D2 所示。可以看出，常规测试过程的回报分别在-100 和-150左右，根据式（11）对回报函数的定义可知，施加GCN-DDPG 融合模型生成的直流电流控制方案后，整体电压恢复效果更佳。

为了进一步验证GCN-DDPG 融合模型的有效性和优越性，从常规测试样本中随机抽取某样本，该样本负荷水平为100 %，发电机组全部开机，线路2-4断开，故障发生在线路9-10的节点9近端，故障发生后，节点9 的电压为全网最低值，直流电流控制方案、节点9的电压分别如图3（a）、（b）所示。图中：Id、U为标幺值，后同。

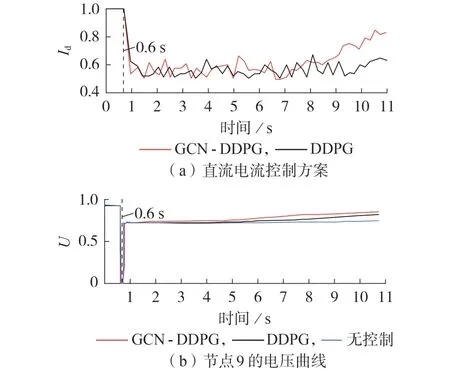
图3 常规测试样本的直流电流控制方案及电压曲线Fig.3 DC current control scheme and voltage curve of normal test sample

从图3（b）可以看出：施加直流电流控制方案后，节点电压在故障后10 s 内均恢复至0.8 p.u.以上；而不施加控制直流电流控制方案时，故障位置节点电压低于0.8 p.u.，电网电压失稳。施加基于GCNDDPG 融合模型的紧急控制模型生成的直流电流控制方案后，节点电压恢复更快，根据图3（a）可知，该方案下直流传输能量降低3.86 p.u.；而施加基于DDPG 模型的紧急控制模型所生成的直流电流控制方案后，直流传输能量降低4.32 p.u.。可见，基于GCN-DDPG 融合模型的紧急控制模型所生成的直流电流控制方案能够在降低较少直流传输能量的情况下，实现节点电压更快、更好地恢复。其他测试样本均具有类似结果。

受端电网频率变化曲线如附录D 图D3 所示。由图可见：由于t=0.6 s 时线路9-10 的节点9 近端发生三相短路接地故障，受端电网无功消耗增加，有功消耗降低，受端电网短暂有功过剩，出现频率尖峰；t=0.7 s 时继电保护动作，频率快速下降并在100 ms内快速恢复至50 Hz 附近，并未引发切负荷等紧急频率控制；t=0.9 s 时本文所提受端电网暂态电压稳定紧急控制启动，直流电流控制方案下达给直流控保系统，由于直流传输有功降低，受端电网频率在t=0.9 s 时开始下跌，并在t=1.1 s 左右达到频率最低点49.83 Hz，此后频率逐渐恢复，最终维持在49.8 Hz以上，可见受端电网频率稳定。对于其他样本，经验证受端电网均能维持频率稳定，由于篇幅所限，频率变化曲线未一一列出。

通过GCN 对电网拓扑进行表征后，GCN-DDPG融合模型相对于常规DDPG 模型而言，在节点特征矩阵X的基础上增加了表征节点连接关系的邻接矩阵A，各节点连接关系信息得到补充。此外，由于暂态电压稳定问题属于局部问题，故障位置近区节点信息具有更高的相关性，依赖GCN 对电网拓扑结构的感知，各个节点到故障位置的距离一定程度上得以表征，因此特征矩阵X中各个元素的相关性得到了补充。可以认为，通过GCN 替换DDPG 网络结构中的部分全连接网络层实现对电网拓扑进行表征，可在图卷积过程中实现更加有效的信息筛选和降维，从而有利于生成更为合理的动作。

基于GCN-DDPG 融合模型与常规DDPG 模型的紧急控制模型泛化测试过程回报如附录D 图D4 所示。由图可见：GCN-DDPG 融合模型泛化测试样本回报均大于-300，针对未曾训练过的样本能够生成有效的紧急控制策略，即所有泛化测试样本下，电压均恢复至0.8 p.u.以上；而对于常规DDPG模型，出现部分泛化测试轮次回报低于-500 的情况，可知这部分样本下，电压恢复较差，甚至最终也未能满足暂态电压稳定标准。

为了进一步验证GCN-DDPG 融合模型的有效性和优越性，随机抽取某泛化测试样本，负荷水平设置为70 %，发电机G2不开机，稳态拓扑线路4-5 断开，三相短路接地故障发生在线路9-14 的节点14近端，故障发生后，节点14 的电压为全网最低值，生成的直流电流控制方案及节点14 的电压曲线分别如图4（a）、（b）所示。

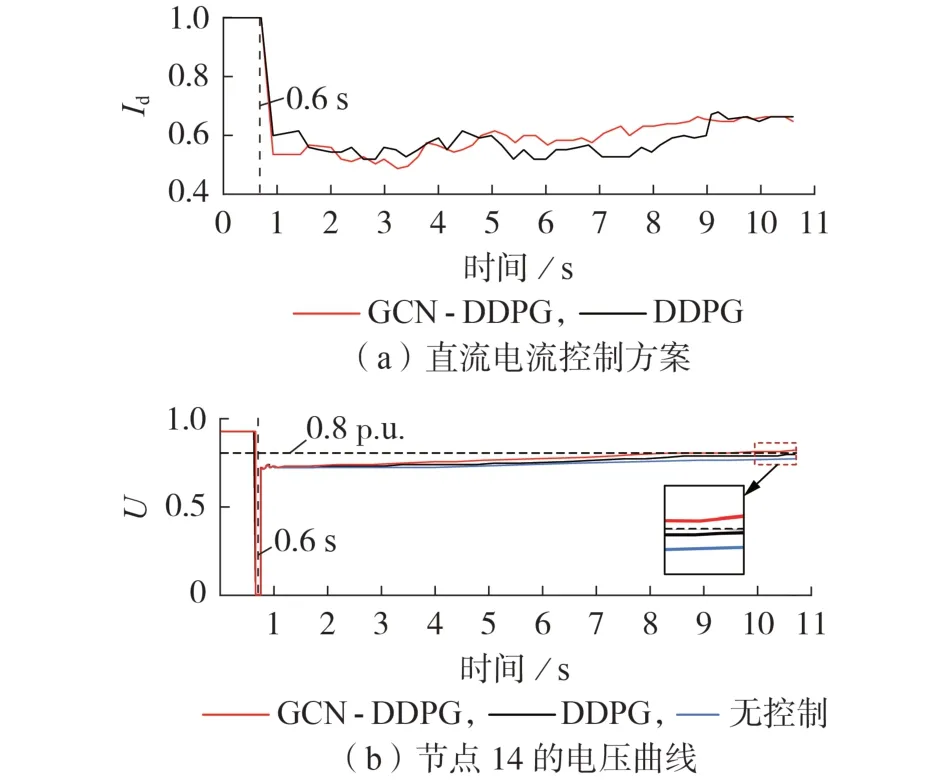
图4 某泛化样本的直流电流控制方案和电压曲线Fig.4 DC current control scheme and voltage curve of generalization test sample

从图4（b）可以看出：不施加控制或施加基于常规DDPG 模型生成的紧急控制策略时，节点14 的电压低于0.8 p.u.，电网电压失稳；而施加基于GCNDDPG 融合模型的紧急控制策略后，节点电压恢复至0.8 p.u.以上。从图4（a）可以看出：基于GCNDDPG 融合模型与常规DDPG 模型的紧急控制模型生成的直流电流控制方案传输能量分别降低了4.14 p.u.和4.27 p.u.。其他泛化测试样本也均具有类似结果，可见，针对泛化测试样本，即训练过程中未曾出现的样本类型，基于GCN-DDPG 融合模型的紧急控制模型在电压恢复效果和降低较少直流传输能量方面取得了更为稳定且优越的结果。

4 结论

为应对直流受端电网暂态电压稳定问题，本文基于直流逆变站可用作受端电网的紧急无功电源的思想，为了高效快速获取紧急控制策略，即直流电流控制方案，并使其适应不同的电网运行方式和故障位置，尤其是电网拓扑结构的变化，提出了GCNDDPG 融合模型，并基于GCN-DDPG 融合模型构建紧急控制模型，用于在线量化计算得到紧急控制策略。通过对比本文所提基于GCN-DDPG 融合模型的紧急控制模型与基于DDPG 模型的紧急控制模型的有效性和优越性，得出如下结论：

1）本文提出的基于GCN-DDPG 融合模型的紧急控制模型应对不同的测试样本和和泛化测试样本，均能在线生成相应的紧急控制策略，即直流电流控制方案，以维持电网暂态电压稳定；

2）基于GCN-DDPG 融合模型的紧急控制模型与基于DDPG 模型的紧急控制模型相比，所生成的直流电流控制方案能使电网电压更快地恢复，而控制代价，即直流能量传输的减少量与基于DDPG 模型的紧急控制模型生成的方案相比要更小，能够在一定程度上降低控制代价，同时提升暂态电压恢复效果。

本文研究目前以直流电流为单一控制变量来应对新型直流受端电网的暂态电压稳定问题，后续工作将包括以下两方面：

1）通过结合判据1 与判据2 制定更为严苛的暂态电压稳定标准来提高电压故障后的恢复效果；

2）考虑到强化学习的优势在于应对更大规模的复杂电网，快速生成紧急控制策略，将直流电流控制与调相机出力调整、切机／切负荷等措施进行协同控制，并进一步考虑多种稳定形态约束的紧急控制策略及大规模算例分析将在未来研究中开展。

附录见本刊网络版（http：//www.epae.cn）。