西北电网330 kV尖樊线人工短路试验中接地距离保护适应性分析

2024-03-26李怀强张健康蒋嘉桁任龙飞张晨浩宋国兵

电力自动化设备 2024年3期

李怀强，张健康，蒋嘉桁，任龙飞，张晨浩，宋国兵

（1.国家电网有限公司西北分部，陕西西安 710048；2.西安交通大学电气工程学院，陕西西安 710049）

0 引言

近年来，以风电为代表的逆变型新能源场站广泛接入电网，使得电源性质相对传统同步机发生了变化，给以距离保护为代表的传统保护带来挑战［1-2］。

距离保护以测量阻抗反映故障距离，其保护范围与灵敏度受系统运行方式的影响较电流保护更小［3］。然而过渡电阻的存在使得距离保护仍受两侧故障电流的影响，同时逆变型电源的弱馈特性有可能放大过渡电阻的影响，降低距离保护的灵敏度和可靠性。文献［4-5］分析了双馈风电场对距离保护的影响，但是仅考虑了新能源场站的频率偏移特性和谐波对工频量提取的影响，并未考虑新能源场站弱馈特性对过渡电阻影响的放大作用。文献［6］分析了全功率换流器型新能源场站对距离保护的影响，但是分析完全依赖于仿真。文献［7-9］在考虑逆变型电源负序电流抑制的基础上，结合场站侧和网侧的故障电流特征分析了距离保护在两相接地、两相相间和三相接地故障下的性能。文献［10］基于文献［6］的仿真分析了光伏场站送出线单相接地故障情景下距离保护的适应性，但并未进行理论分析。因此有必要进一步分析发生单相接地故障时，新能源场站电源故障特征影响距离保护的机理。

西北电网于330 kV 尖樊线组织进行了2次人工短路试验，以检验单相接地故障下距离保护的动作情况，该试验属于近年来陕西电网最大规模的新能源涉网性能扰动试验。本文将概述该试验的场景和操作过程；分析风电场的各种控制策略对故障电流的影响，进而研究单相接地故障下风电场故障特征影响接地距离保护性能的机理；最后结合试验所得保护录波数据和新能源场站电压、电流数据进行验证。

1 试验概况

1.1 系统拓扑

尖樊线为尖山变和樊学变330 kV 联络线，线路长度为22.9 km，其拓扑结构如图1 所示。图中：Um、Un和Im、In分别为樊学变和尖山变保护测量的电压、电流；ZWf、ZGf分别为风电场侧和网侧母线与故障点之间的线路阻抗；Rf为过渡电阻；尖山变接入油房庄风电场，并有尖夏线和尖边线2 条出线；樊学变接入石涝河风电场。

图1 尖樊线拓扑结构示意图Fig.1 Topology of Jian-Fan transmission line

尖山变接入风电场装机容量约为350 MW，樊学变接入风电场装机容量约为200 MW；2 个风电场采用的风电机组包含双馈风机和直驱风机2 种类型，且来自不同厂家。

尖山变通过尖夏线与夏州站相连，通过尖边线与定边站相连，三者形成环网，且夏州站为750 kV变电站，是该地区的主站，故尖山变一侧可以视作大电网。而樊学变不再与相同或更高电压等级的变电站联通，其接入的风电场仅通过尖樊线向外输送功率，不与其他电源连接，故可以认为风电场的故障特征即是樊学变一侧的故障特征，尖樊线是典型的新能源场站送出线。

短路试验地点设置在距樊学变约60 % 线路全长处，故障类型设置为A相接地故障，故障持续时间约为80 ms。

1.2 人工短路试验操作流程

330 kV 架空线路人工短路试验示意图如附录A图A1所示。在尖樊线停电后装设试验用金属棒，该金属棒通过2 根引下线与架空线相连，为短路试验提供安全的接触点，从而避免短路试验影响架空线结构。接地部分由接地线和引弧线构成：接地线固定在杆塔脚部接地；引弧线一端固定在接地线上，另一端固定在弹头上。进行人工短路试验时，通过发射装置将弹头发射到金属棒与引下线中间，通过弹头带动引弧线搭上金属棒并短接，从而形成单相接地故障。故障后，线路保护跳单相；燃起的电弧会将引弧线烧断，在断路器动作后电弧熄灭，单相接地故障在80 ms 内被清除，继而线路重合闸启动，一般在故障后的200 ms 内三相电压、电流全部恢复，线路恢复供电。

2 风电场故障特征

风电场故障穿越策略决定其故障特征，可根据故障穿越策略分析风电场故障电流和等效阻抗。

2.1 正序故障电流

故障穿越时，换流器应输出与正序电压降落成正比的无功电流［11］，同时在不超过电流限值的情况下尽可能输出有功。综合参考文献［11-12］，正序d、q轴电流可表示为：

式中：id+、iq+分别为正序d、q轴电流；P为风电场输入的有功；U+为换流器端口正序电压幅值；Imax为换流器允许流过的最大电流；K1为风电场动态无功电流比例系数；IN为风电场额定电流。

此时风电场侧的正序电流IW+可以表示为：

式中：θ+为换流器端口正序电压相角。

2.2 负序故障电流

关于不对称故障下的控制策略标准［11］在2021年才正式颁布，故较老型号的风机可能采用不同的控制策略，因此需要讨论各种负序控制策略下的负序电流特征。

2.2.1 新标准负序控制策略

新标准要求在发生不对称故障情况时从电网吸收负序动态无功电流抑制负序电压升高；而对负序有功电流没有明确要求，一般控制为0。因此，负序d、q轴电流表达式［11］为：

式中：id-、iq-分别为负序d、q轴电流；K2为风电场负序动态无功电流比例系数；U-为换流器端口负序电压幅值。

应注意的是，新标准将发生不对称故障时正序无功电流动态调节对应的正序电压范围变为了0.6～0.9 p.u.，实际减小了输出正序无功电流的上限。根据文献［12］试验所得结论，各型号的风机在不对称故障下普遍会减小输出的无功功率。

2.2.2 不采取负序控制策略

如果风机不采取负序控制策略，则其换流器仅输出正序电压，因此在负序网络中无负序电压源。此时的风机可以等效为纯阻抗，该阻抗包含滤波电感和电力电子开关导通电阻。

2.2.3 传统负序控制策略

在不对称故障下，只可选择对4 个功率量或者对2 个负序电流进行控制［13］，根据选取受控量的不同有3 种实用的控制策略［14］：①抑制负序电流为0；②抑制有功功率二倍频分量；③抑制无功功率二倍频分量。

在负序旋转坐标系d轴与负序电压同步的前提下，负序q轴电压uq-=0，根据文献［15］提出的3种控制策略的统一表达形式，可以得到负序d、q轴电流表达式为：

式中：K为控制策略相关参数，K取值为0、1、-1分别对应抑制负序电流为0、抑制有功二倍频分量、抑制无功二倍频分量策略。

应注意的是，在采取抑制有功或无功二倍频分量策略时，由于id-≠ 0，在正常输出有功时id+的表达式为：

在明确了负序d、q轴电流后，风电场侧的负序电流IW-可以表示为：

式中：θ-为换流器端口负序电压相角。

特别地，由式（4）、（6）可知，采用抑制有功或无功二倍频分量控制策略时，风电场侧的负序电流和正序电流幅值有如下关系：

2.3 双馈风机故障电流

2.3.1 投入Crowbar电路

在发生故障后，双馈风机检测到转子过电流和直流过电压时，会迅速投入Crowbar电路以保护转子侧换流器。此时转子侧换流器被旁路，双馈风机可视为一台转子侧带大电阻的异步电机［16］，其正、负序等值阻抗为［17］：

式中：Zeq+、Zeq-分别为双馈风机正、负序等效阻抗；Rr和Xr分别为转子电阻和漏抗；Rc为Crowbar 电阻；Xm为风机励磁电抗；Rs和Xs分别为定子电阻和漏抗；s为转差速率。

双馈风机的s∈[-0.3，0.3]。双馈风机处于超同步运行时，-0.3≤s＜0，双馈风机的正序等效阻抗的电阻分量为负，而其他情况下均为正。双馈风机的负序等效阻抗在任何情况下都为正阻抗。

双馈风机投入Crowbar电路时，故障电流中除了工频分量外，还有衰减直流分量和衰减转速频率分量［18］。保护测量时会进行差分滤波处理以滤除衰减直流分量，单相接地故障下衰减转速频率分量比例非常小，对离散傅里叶变换相量计算和测量阻抗影响很小［19］，因此可以忽略两者对距离保护的影响。

2.3.2 未投入Crowbar电路

如果双馈风机未投入Crowbar电路，在故障穿越时其可以通过控制转子侧电流控制定子侧电流，与直驱风机的故障特征几乎相同。根据文献［20-21］，3 种负序控制策略下的双馈风机正序定子电流和网侧换流器电流为：

式中：isd+、isq+分别为双馈风机正序定子电流的d、q轴分量；igd+、igq+分别为网侧换流器电流的d、q轴分量；Ps为定子应输出的有功；Isd，max为定子侧换流器d轴电流限值，与转子侧电流限值、转子q轴电流有关；Pg为网侧换流器应输出的有功。

双馈风机输出电流为定子电流和网侧换流器输出电流之和，而负序电流与正序电流的关系与直驱风机相同，如式（4）所示。

3 接地距离保护适应性分析

3.1 保护原理

接地距离保护的测量阻抗计算公式［22］为：

式中：m、n 分别表示风电场侧和网侧；Zxϕ为x侧ϕ相测量阻抗；Uxϕ、Ixϕ分别为x侧的ϕ相测量电压、电流；Ix0为x侧的零序测量电流；KZ为零序补偿系数。

以发生A 相接地故障时的风电场侧保护为例，在不考虑线路电容的情况下，可以认为保护测量电流就是风电场输出电流。由图1 可知，风电场侧的故障相测量电压为：

式中：IWA为风电场侧A 相故障电流；IW0为风电场侧零序故障电流；IGA为网侧A相故障电流。

将式（11）代入式（10）可得风电场侧故障相测量阻抗与过渡电阻的关系为：

式中：KR为附加阻抗系数。

可见KR越大，附加阻抗越大，测量阻抗就越偏移实际的线路阻抗；如果KR的相角接近 -90°，则附加阻抗呈容性，将引起稳态超越问题，导致发生区外故障时保护误动。KR实际表征了两侧电流对附加阻抗的影响，因此分析两端电源对接地距离保护影响机理的关键就是分析两侧电流与KR的幅值和相角的关系。

3.2 两侧电流对附加阻抗的影响

由于风电场的正、负、零序电流相互独立，为便于讨论，将式（12）中的相电流替换为序电流，可得风电场侧保护的附加阻抗系数KRm如式（13）所示。

式中：IW+、IW-分别为风电场侧正、负序故障电流；IG+、IG-、IG0分别为网侧正、负、零序故障电流。

同理可得网侧保护的附加阻抗系数KRn如式（14）所示。

由式（13）、（14）可知，风电场侧和网侧正、负、零序电流之间的相对关系决定了附加阻抗系数的幅值和相角，下面讨论电流之间的相互关系。

3.2.1 电流幅值

A 相接地故障的复合序网图［23］如图2 所示。图中：UW+、UW-分别为风机端口的正、负序电压；UG+为网侧正序电压；Uf+、Uf-、Uf0分别为故障点处正、负、零序电压；If+、If-、If0分别为正、负、零序故障电流；ZW+、ZW-分别为故障点到风机端口正、负序等效阻抗，包含ZWf、风电场侧主变等效阻抗、集电线路等效阻抗和箱变等效阻抗；ZW0为故障点到风机端口零序等值阻抗，包含ZWf、风电场侧主变等效阻抗；ZG+、ZG-、ZG0分别为网侧正、负、零序等效阻抗，包含ZGf和网侧系统等效阻抗。

图2 A相接地故障复合序网图Fig.2 Composite sequence network diagram of phase-A grounding fault

发生A 相接地故障时，正、负、零序网络串联，因此If+=If-=If0，且If+=IW++IG+。网侧系统为强源，可以提供很大的故障电流；而综合风电场各种故障穿越策略可知，针对风电场的正序电流有着严格的限流策略，因此风电场侧能提供的正序电流很小，只略微大于额定电流。因此可以认为网侧正序电流远大于风电场侧正序电流，故障电流中网侧正序电流占主导。

对于负序电流，采用抑制有功或无功控制策略时，由式（7）可得风电场的正、负、序电流幅值与正、负、序电压幅值比相等，而一般情况下风机端口负序电压小于正序电压，故负序电流幅值小于正序电流幅值。如果风电场采用新标准控制策略，由于负序电压一般较小，提供的负序电流也不大。如果风电场不采取负序控制策略，或者双馈风机投入Crowbar电路，则风电场的负序等效阻抗呈阻感性质，且其阻抗较大，负序电压又较小，故负序电流仍然很小。综上所述，在各种控制策略下，风电场提供的负序电流都远小于网侧提供的负序电流。

对于零序电流，由于采用Y／△接线，两端背侧系统都被隔离，风电场侧与网侧零序电流的相对大小取决于两侧零序阻抗的大小。两侧零序阻抗包含线路阻抗和变压器阻抗，一般情况下，线路阻抗远小于变压器阻抗，因此故障点位置不同造成的两侧线路阻抗差异对两侧零序电流分流的影响可以忽略。对于风电集中送出的场景，风电场侧的变压器阻抗仅是风电场主变阻抗和少数下级线路变压器阻抗的并联；而网侧则接入大电网，网侧母线不仅与本地的变压器连接，还与其他地区变电站的母线和变压器相连，因此网侧并联的变压器多于风电场侧，一般情况下网侧零序阻抗小于风电场侧零序阻抗，风电场侧分流流过的零序电流也更小。另一方面，风电场侧零序电流不受风电场电流限值的影响，因此风电场侧零序电流一般大于正、负序电流。

进一步讨论网侧正、负、零序电流之间的相互关系。对于单相接地故障，正、负、零序故障电流相等，因此有如下关系：

由于风电场侧正、负序电流幅值均远小于网侧，因此可以近似认为网侧正、负序电流相等；而风电场侧零序电流幅值同样小于网侧零序电流，但幅值差距小于正、负序电流，因此网侧零序电流幅值稍小于网侧正、负序电流。

3.2.2 电流相角

要分析风电场侧附加阻抗系数的相角，则必须明晰两侧正、负、零序电流的相角。而由前文可知，网侧正、负、零序电流相角近似相等。因此以网侧电流为基准，分别讨论风电场侧正、负、零序电流的相角。

对于正序电流，以正序故障电压Uf+为中介分析两端电流相角差。对于网侧正序电流IG+，在忽略风电场侧电流影响的前提下，有如下关系：

由于网侧阻抗以变压器和线路阻抗为主，可认为ZG0和ZG-近似为电感，则在Rf很小时，IG+落后Uf+近90°，随着过渡电阻的增大，相差角度逐渐减小。

风电场侧正、负序电流相量图如图3 所示。由图3（a）可知，对于风电场侧电流，以UW+为相量图基准，Uf+与IW+有如下关系：

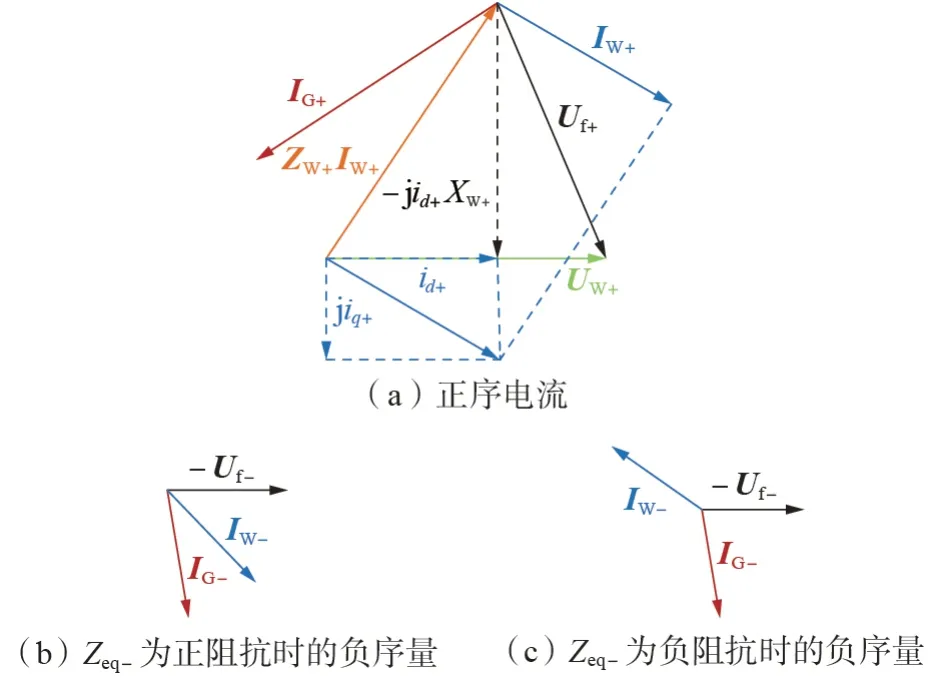
图3 风电场侧正、负序电流相量图Fig.3 Phasor diagram of positive- and negative-sequence current at wind farm side

式中：XW+为ZW+的电抗分量。由于ZW+中以变压器和线路阻抗为主，因此可以认为ZW+近似为电感。

随着风机出力的减小，id+减小，Uf+的垂直分量减小，Uf+逆时针旋转，而IW+的水平分量减小，顺时针旋转，因此IW+超前Uf+的角度减小，甚至可能落后于Uf+。一般情况下，IW+超前IG+的角度在(0°，180°)范围内；但随着风机出力的减小，过渡电阻增大，IW+超前IG+的角度减小。在风机出力较小和过渡电阻较大的情况下，IW+可能落后IG+。

对于负序电流，可通过分析两侧的负序等效阻抗判断两侧负序电流与负序故障电压的相角关系。

网侧负序阻抗ZG-近似为电感，因此IG-落后-Uf-近90°；而风电场侧负序等值阻抗由负序控制策略决定。

在采取抑制有功或无功二倍频分量的控制策略时，风电场负序等效阻抗为：

采用抑制有功二倍频分量策略时，K=1，同时id+＞0、iq+＜0。因此Zeq-的相角在(0°，90°)范围内，Zeq-呈正阻抗性质。由于要输出一定的有功，因此Zeq-的电阻分量较大，与纯电感有很大的差异，同时由于风电场输出负序电流的幅值小，Zeq-的幅值远大于ZW-，进而风电场侧总负序等效阻抗也有较大的电阻分量。最终可以认为IW-滞后-Uf-的角度在(0°，90°)范围内，但离滞后90°仍有一定差异，如图3（b）所示。因此IW-超前IG-的角度在(0°，90°)范围内，两者仍有一定相角差。

类似的情况有双馈风机投入Crowbar电路时，风机同样呈正阻抗性质，且电阻较大。

而采用抑制无功二倍频分量策略时，K=-1，因此Zeq-的相角在(-180°，-90°)范围内，呈现负阻抗性质，同样由于风电场输出负序电流幅值小，风电场侧总负序等效阻抗仍表现为负阻抗性质，如图3（c）所示。进而IW-超前-Uf-的角度在(90°，180°)范围内，IW-滞后IG-的角度在(0°，180°)范围内。

对于采取新标准负序控制策略的情况，风电场负序等效阻抗为：

可见风电场可等值为纯电感，进而风电场侧总负序等效阻抗也近似为纯电感，IG-与IW-的相角相差不大。风电场不采取负序控制策略时也存在类似的情况，因为其等效阻抗主要是滤波电感。

对于零序电流，两侧阻抗的成分都是线路和变压器的阻抗，都近似为电感，因此两侧零序电流的相角差很小，进而与网侧正、负序电流的相角差也很小。

3.2.3 附加阻抗系数

由于风电场的正、负、零序电流都小于网侧，因此可以近似忽略式（13）、（14）分母中的风电场侧电流，简化附加阻抗系数的表达式。可得风电场侧的附加阻抗系数如式（20）所示。

进一步分析式（20）的分母可知，风电场侧零序电流的系数1+3KZ显然大于1，这增大了零序电流的占比，而零序电流幅值又大于正、负序电流，因此分母中以零序电流为主导，分子、分母的相角差不大，故KRm的相角很小。而风电场侧正、负序电流的幅值远小于网侧，风电场侧零序电流的幅值也小于网侧，故分母幅值远小于分子，KRm幅值很大。进而风电场侧附加阻抗很大，且近似为纯电阻，导致测量阻抗在保护圆外，接地距离保护拒动。

认为网侧正、负、零序电流和正序故障电流近似相等，即If+≈IG+≈IG-≈IG0，可得网侧附加阻抗系数如式（21）所示。

由于实际中网侧的零序电流稍小于网侧正、负序电流，因此实际KRn的幅值更大。但KRn的幅值总小于1，相角近乎为0°，网侧附加阻抗近似为纯电阻，且小于过渡电阻，对接地距离保护的影响很小。

3.3 仿真验证

建立典型风电场送出系统仿真模型验证本文对电流相互关系和附加阻抗系数幅值、相角的定性分析。风电场送出系统仿真模型的拓扑结构如附录A图A2 所示，该模型由风电场等效模型、集电线等效阻抗、风电场主变、330 kV 线路、网侧等效阻抗和网侧电源组成，相关参数如附录A 表A1 所示，故障点设置在线路距风电场60 % 处，Rf= 0.5 Ω。

在采用不同负序控制策略的场景下进行仿真试验。由于未投入Crowbar电路时，双馈风机与直驱风机的故障电流几乎完全一样，因此只对双馈风机投入Crowbar电路的场景进行仿真试验，不同负序控制策略场景下则采用直驱风机进行仿真。风电场侧和网侧电流的幅值、相角仿真结果分别如附录A 表A2、A3 所示。特别地，在风电场采取新标准控制策略时，改变风机出力和过渡电阻的大小，对比两侧正序电流的相角差，以研究风机出力和过渡电阻对正序电流相角的影响，对应的结果如附录A 表A4所示。

分析表A2 可知：网侧正、负序电流的幅值均远大于风电场侧正、负序电流的幅值，而网侧正、负序电流近似相等；风电场侧零序电流小于网侧零序电流，但是大于风电场侧正、负序电流，网侧零序电流稍小于网侧正、负序电流。

分析表A3、A4 可知：一般情况下，风电场侧正序电流相角超前网侧，但超前角度随风机出力的减小、过渡电阻的增大而减小；只有采取抑制无功二倍频分量策略时的负序电流相角和风机出力较小、过渡电阻较大时的正序电流相角，风电场侧相角明显落后于网侧，其余情况均超前或近似于网侧；两侧零序电流的相角差很小；网侧正、负、零序电流的相角近似相等。

各控制策略下的附加阻抗系数仿真结果如附录A 表A5 所示。由表可知：风电场侧附加阻抗系数的幅值很大、相角很小，而网侧附加阻抗系数的幅值小于1、相角接近0°，仿真结果与理论分析一致。

4 试验数据分析

西北电网于330 kV 尖樊线进行了2次人工短路试验（下文分别简称为试验1和试验2），试验结果表明，发生单相接地故障时，线路差动电流保护能正常动作，而接地距离Ⅰ段保护未动作。分析试验数据可知：各风电机组处于未满发状态且出力各不相同；双馈风机的Crowbar 电路实际均未投入；2 次试验的过渡阻抗分别约为0.553 6+j0.052 5、0.538 3+j0.044 1 Ω。

4.1 测量阻抗

尖樊线两侧各有2套不同型号的保护，第1套保护的型号为NSR303，第2 套保护的型号为PCS931。2 次试验中尖山变和樊学变的三相电流、电压录波分别如附录B 图B1 和图B2 所示，尖樊线接地距离Ⅰ段保护相关定值和线路参数如附录B 表B1 所示。测量数据均为二次侧数据。

以试验2 中保护PCS931 的记录数据为例，尖山变和樊学变的测量阻抗分别见图4（a）、（b）。对发生故障时的数据取平均值，可得尖山变和樊学变的测量阻抗分别为1.606 8∠63.84° Ω和3.432 5∠30.69° Ω。

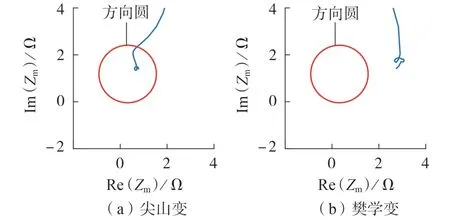
图4 保护测量阻抗Fig.4 Measured impedance of protection

由图4 可知：发生故障时，尖山变的测量阻抗进入方向圆内，而樊学变测量阻抗始终在方向圆外。因此尖山变保护能够正确动作，而樊学变保护不能正确动作。并且樊学变测量阻抗明显向右偏移，阻抗角减小，说明附加阻抗含有很大的电阻分量，这与理论分析一致。2 次试验中，不同型号的保护装置得到的测量阻抗数据如表1 所示，由表可验证以上结论。

表1 测量阻抗试验结果Table 1 Experimental results of measured impedance

4.2 电流幅值相位和附加阻抗系数

2 种型号的保护装置均可得到对侧同步电流数据，因此可以实现两端电流幅值和相位的比较，并计算附加阻抗系数。

樊学变测量的A相故障电流波形如附录B图B3（a）所示。由图可见，尖山变的故障电流远大于樊学变的故障电流，前者能达到后者的约8倍。

樊学变保护安装处的正、负、零序电压幅值如附录B 图B3（b）所示。由图可见：负序电压幅值明显小于正序电压幅值；故障时正序电压幅值减小为非故障时的三分之一左右。2 次试验中保护安装处测量得到的正、负、零序电压幅值如附录B 表B2 所示。由表可见，2 次试验中，发生故障时的电压差异不大，这可能是由于所用的人工短路试验装置是同一型号，过渡电阻近似相等。

樊学变保护安装处的正、负、零序电流幅值如附录B图B3（c）所示。由图可以看出：樊学变的正、负、零序电流幅值都远小于尖山变；樊学变的零序电流幅值最大，负序电流幅值最小；尖山变的正、负、零序电流幅值差异相对较小。两侧正、负、零序电流幅值如附录B 表B3 所示。对比两侧电流幅值可以发现：风电场侧负、零序电流和网侧正、负、零序电流的2次试验结果差异不大；以网侧正序电流幅值为基准，网侧负序电流幅值与网侧正序电流幅值几乎相同，网侧零序电流幅值约为网侧正序电流幅值的75 %；风电场侧负、零序电流幅值分别约为网侧正序电流幅值的5 %、25 %；而风电场侧正序电流在2 次试验中的结果则有很大差异，这主要是因为2 次试验中风电场出力不同，根据非故障时的数据，试验1 中风电场侧送出的有功约为试验2 的三分之一，因此试验1 中风电场输出的正序d轴分量要小于试验2，根据前文分析，风电场侧正序电流超前网侧的角度更小。

表2 为风电场侧与网侧正、负、零序电流的相角差。由表可见：试验1 的相角差的确小于试验2；风电场侧正、负序电流超前网侧正、负序电流；两侧零序电流的相角差很小。

表2 风电场侧与网侧电流相角差Table 2 Phase difference of current phase between wind farm side and grid side

根据两侧电流计算得到的附加阻抗系数如表3所示。由表可见：网侧附加阻抗系数与理论分析一致，近似于1/(1+KZ)≈0.662 3；风电场侧附加阻抗系数幅值较大，在4 以上，而相角为很小的负数，这将导致樊学变保护的附加阻抗近似纯电阻性质，且为过渡电阻的4倍，从而引起保护拒动。

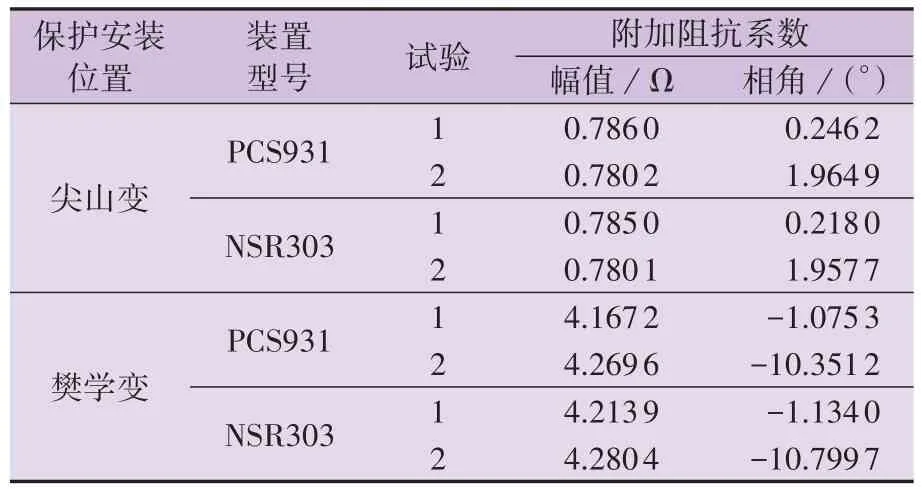
表3 附加阻抗系数的计算结果Table 3 Calculation results of additional impedance coefficient

4.3 保护性能提升方案

由于风电场侧接地距离保护附加阻抗近似纯电阻，在阻抗复平面上测量阻抗相对于实际故障点到母线之间的线路阻抗水平向右偏移，垂直方向上偏移很小。根据这个特性，增大水平方向的保护动作范围，可以提高保护的耐受过渡电阻能力；而垂直方向的保护动作范围不变，在线路发生区外故障时，测量阻抗的垂直分量仍在保护范围外，接地距离保护不误动。

相对于方向圆特性，采用四边形特性［24］时可以分别调整水平和垂直方向的动作范围。风电场侧保护可采用四边形特性，根据实际的线路保护长度设定电抗整定值Xset，根据躲过最大负荷设定电阻整定值Rset［25］。