非线性ABS 系统全局滑模控制律设计

高 众，肖 平，张宇华

（1.安徽工程大学机械工程学院，安徽，芜湖 241000；2.安徽大昌科技股份有限公司，安徽，芜湖 241000）

0 引言

防抱死制动系统（ABS）作为提高车辆安全性和可靠性的重要部件，主要功能是在汽车制动过程中，避免由车速和轮速的不一致导致车轮抱死而提高车辆制动效果[1]。文献[2]和[6]针对车辆ABS 系统，提出了一种改进的MPC 控制策略。但所提出的MPC 控制模型要求实时进行矩阵求逆运算，目前无法很好地解决这个运算问题，暂时无法应用到实际车辆ABS 系统。文献[3]和文献[4]所描述的滑移率控制策略，是将模糊控制和神经网络结合在一起，通过对网络不断的调试和训练，从而将车轮滑移率曲线能够稳定在0.2 附近，但其花费的时间和经济成本相对于其他控制策略偏高，也无法将其应用到实际。文献[5]首先设计了一种干扰观测器，然后通过设计非线性滑模控制器来消除系统中的干扰，提高了滑移率控制效果。但其针对的是单轮模型，而单轮模型无法准确描述车辆运动，不确定性太高。文献[7]在对车轮打滑控制设计策略、评估及在防抱死制动系统中的应用进行综述，最后开发了一种基于新负载传感技术的非线性模型预测控制设计。文献[8][9][10]均针对滑模控制器提出了新的滑模面，但没有改进滑模面的趋近律，并延长了系统到达滑动表面的时间，并且到达滑模面附近产生了很大的抖振。

本设计采用滑模控制方法对车轮滑移率进行快速控制。首先建立关于车辆四轮模型的ABS 系统数学模型；为了消除传统线性滑模面的到达模式，新设计了一种全局滑模面，即在传统滑模面基础上加入补偿函数，并针对传统趋近律使系统运动在进入滑模面后产生抖振，新设计了一种改进指数趋近律；最后仿真结果表明，本研究所提出的全局滑模控制方案具有较好的制动性能，其车轮滑移率保持在理想的车轮滑移率附近，从而减少了抖振问题。

1 ABS 系统数学模型

由于ABS 系统有很强的非线性和不确定性，真实的车轮动力学模型很难获得，为了简化问题设计研究四轮车辆模型，如图1 所示。

图1 四轮车辆模型Fig.1 Four wheel vehicle model

基于传统的汽车行驶动力学模型，由图1 所示的车辆受力分析，建立非线性动力学方程[11]。

式中，ωi(i=1,2,3,4)分别表示前左，前右、后左、后右车轮的角速度(rad/s)，Tbi(i=1,2,3,4)分别是四个车轮的制动扭矩，Fxi(i=1,2,3,4)分别代表四个车轮所受到的纵向力(N)，Ri(i=1,2,3,4)分别是四个车轮半径，且假设R1=R2=R3=R4=R，Ji(i=1,2,3,4)分别是四个车轮的惯性矩(kg·m2)，且假设J1=J2=J3=J4=J。

式中，FN1、FN2表示前左、前右车轮所承受的正常载荷(N)[14]，m为汽车的总质量(kg)，L2表示汽车后轮轴到车辆质心的距离(m)，g为重力加速度(m/s2)，a是纵向车辆加速度(m/s2)，h为车辆质心的高度(m)，L为汽车前轮轴到后轮轴之间的距离(m)。

式中，FN3、FN4表示后左、后右车轮所承受的正常载荷(N)，L1表示车前轮轴到车辆质心的距离(m)。

式中，μ(λi)是道路轮胎附着力系数，它是关于每个车轮滑移率λi的函数。

式中，V是纵向车辆速度(m/s)。

汽车行驶时，车轮滑移率λi被定义为：

在实际ABS 系统中，滑移率λ应控制在最佳滑移率λd=0.2，对应于峰值粘着系数μmax，以最大限度地利用地面粘着。然而，制动力受道路环境的影响，许多经验表达式和分析表达式已发展出道路轮胎摩擦系数μ(λ)。在本研究中，使用了魔术公式(MF)模型，其给出如下。

其中，B是刚度系数，C是形状系数，D是峰值，E是曲率系数。这些系数取决于道路条件，本研究选择干混凝土路面和湿沥青路面两种情况进行模拟分析。两种路面参数分别为，干混凝土路面：B=6.0，C=2.2，D=0.9，E=0.98；湿沥青路面：B=6.0，C=2.1，D=0.78，E=0.8。借由simulink 绘制出路面附着系数μ和滑移率λ之间的关系图。

由图2 可知，最佳滑移率约为0.2，也是ABS控制器的最佳控制目标。

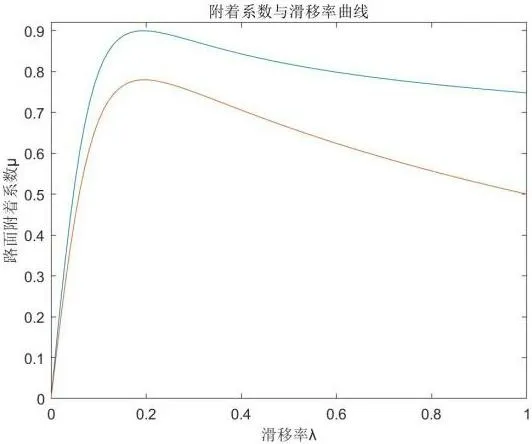
图2 附着系数与滑移率关系Fig.2 Relationship between adhesion coefficient and slip rate

2 ABS 系统滑模控制器设计

滑模控制（sliding mode control,SMC）也叫变结构控制。针对滑模控制器的特性，其设计的关键步骤有两个，首先就是要根据该非线性系统设计合适的滑模面s，能够使系统的状态在有限时间内可以沿滑模面以指数速度趋向于0。第二点就是设计趋近律，寻找滑模面s 与控制律u 之间的关系，以保证滑模面s 能够趋近于0。

通过设计一种新型滑模控制器，使车轮滑移率在尽可能短的时间内控制在0.2。设车轮滑移率期望值为λd，则滑移率误差公式为：

2.1 滑模面设计

对于传统的线性滑模面来说，其公式表示为：

其中，K＞0。传统滑模控制的系统响应可分为两部分：到达模式和滑动模式。其鲁棒性仅存在于滑模阶段，即如果x(t)到达滑模面，则s 在有限时间内趋向于0，而如果x(t)未到达滑模面，那么最终s 会收敛于一个时变的量，因此无法确保鲁棒性能。与传统的滑模控制相比，全局滑模控制具有很强的鲁棒性。全局滑模控制设计的关键就是在滑模切换函数中引入了非线性函数，从而消除了控制系统的到达模式。

对于非线性全局滑模面来说，其公式表示为：

函数f(t)能够保证系统的滑模运动在开始时位于滑动表面上，它可以将任意状态空间中的系统状态直接驱动到滑动表面。为此，f(t)应满足以下条件：

其中，式(13)是表示滑模面的初始位置，式(14)是保证滑模面的渐近稳定性，式(15)是保证滑模面的存在性。M为大于零的任意正数。由以上三个条件可设f(t)为：

其中，η＞0。由式(16)可知，f(t)满足(13)(14)(15)三个条件。

现将式(16)代入式(12)中，可得ABS 非线性全局滑模面为：

将式(16)代入式(13)中，有：

其中，λ0和λd0分别表示λ和λd的初始状态，且λ0=0，则对于(18)，有：

将式(19)代入式(17)中，得到ABS 非线性全局滑模面函数为：

2.2 滑模控制律设计

在上一节中，针对该ABS 系统设计了一种全局滑模面s x,t ，且能保证系统的渐近稳定性。接下来根据设计的滑模面来确定滑模控制律，使其满足在有限的时间内将系统的状态轨迹驱动到滑模表面上，并保持在滑模表面上。

对于传统的等速趋近律，其公式表示为：

对于传统的指数趋近律，其公式表示为：

其中，ε＞0，ε1＞0，ε2＞0，sgn 为符号函数。-ε2s(x,t)是指数趋近项，ε2越大，趋近滑模面速度越大；-ε1sgn(s)是等速趋近项，是为了消除抖振。趋近律式(22)将在系统的平衡点附近产生一定的抖振。系统状态无法最终收敛到平衡点，这意味着滑移率最终无法达到预期值。主要原因分析如下：当系统的状态达到滑模面时，s(x, t)非常小，式(22)中的第一项ε1sgn(s(x,t))起主要作用。但它只是一个常数，不能保证系统的状态收敛到原点，惯性的影响会引起一定幅度的抖振。

为了更好地解决以上问题，设计了一种新的指数趋近律：

其中，α1＞0，α2＞0。

对趋近律式(23)进行分析，当系统状态未到达滑模面时，s(x, t)较大，此趋近律等同于式(22)，并且由于引入了ln(1+|α1·s(x,t)|))·|α2·s(x,t)|，到达滑模面速度会更快。当系统状态到达滑模面附近时，s(x,t)较小，ln(1+|α1·s(x,t)|))趋向于0，控制律的到达速度慢得多，这样惯性会相对式(22)较小，意味着抖振显著减小。

在(8)式中，Tbi即系统需要设计的控制量u，考虑滑模面s=0 及s≠0 两种情况，分别设计滑模等效控制量u1和补偿不连续控制量u2[12]。即：

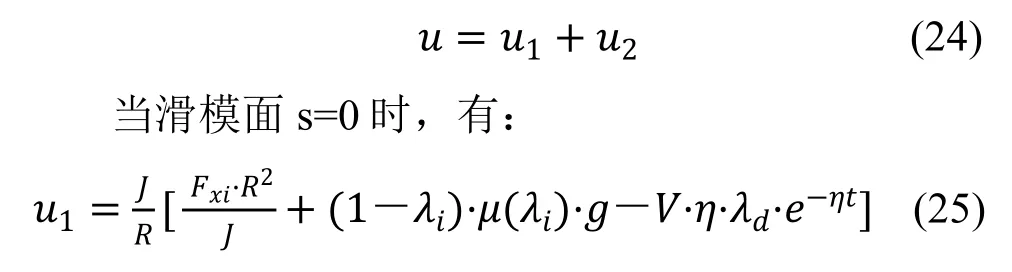
当滑模面s≠0 时，有：

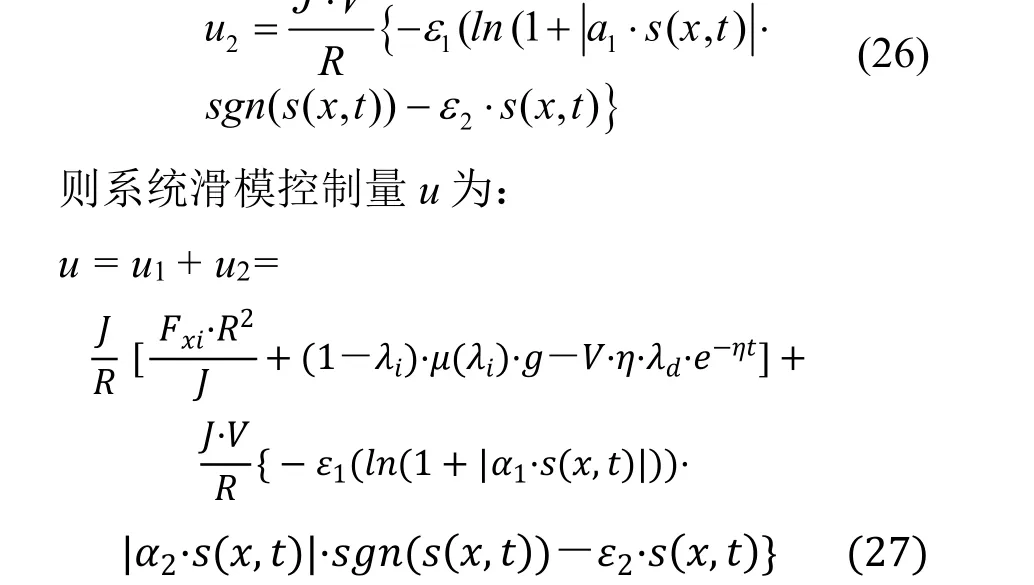
2.3 Lyapunov 意义下的稳定性证明

现定义一个能量函数，即Lyapunov 函数为：

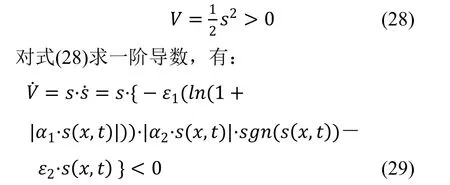
满足Lyapunov 意义下的稳定。

3 仿真分析

在本节中，通过Matlabsimulink 模块对该ABS 系统所设计的全局滑模控制方案进行验证。通过比较传统滑模控制器，传统全局滑模控制器和提出的全局滑模控制器分别在干混凝土路面和湿沥青路面下的制动性能。

针对本次所研究的四轮车辆模型，公式中所涉及的主要参数如表1 所示。

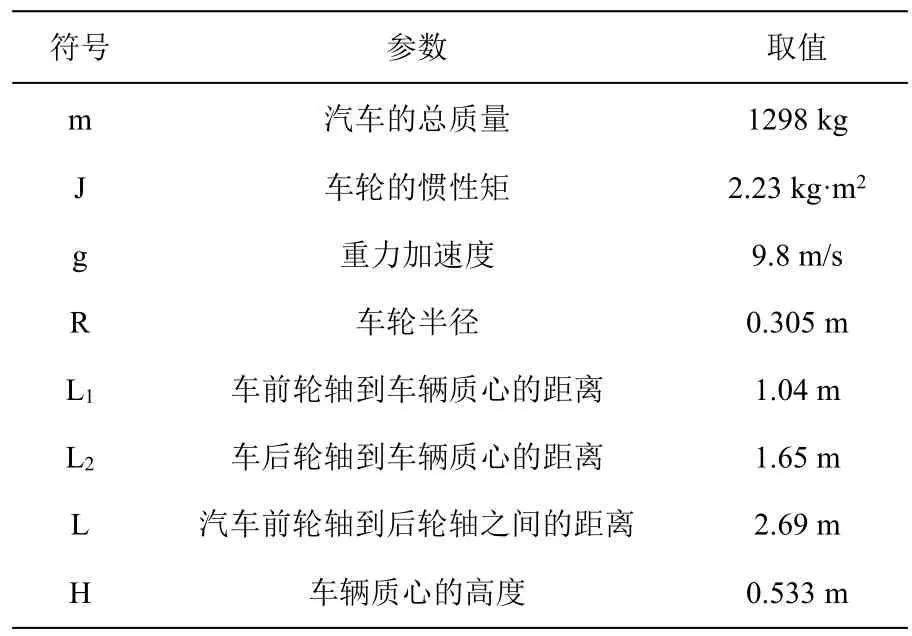
表1 ABS 系统参数表Table l ABS system parameters

首先，对无控制器的非线性ABS 系统加入控制输入Tbi进行了仿真研究。即，假设初始速度为50 m/s ， Tb1=Tb2=800 N·m ， Tb3=Tb4=200 N·m。根据公式(1)建立车轮角速度求解模型(以前左车轮为例)，该模型能够得出车辆行驶中各个车轮的角速度，如图3 所示。

图3 车轮角速度模型实现图Fig.3 Ⅰmplementation diagram of wheel angular velocity model

根据公式(5)建立汽车加速度求解模型，对加速度积分即可得到汽车行驶速度，如图4 所示。

图4 汽车速度模型实现图Fig.4 Ⅰmplementation diagram of vehicle speed model

根据公式(8)建立车轮滑移率求解模型(以前左车轮为例)，该模型能够得出车辆行驶中各个车轮的滑移率变化规律，如图5 所示。

图5 车轮滑移率模型实现图Fig.5 Ⅰmplementation diagram of wheel slip rate model

根据公式(9)建立汽车轮胎附着系数求解模型，运用轮胎魔术公式，如图6 所示。

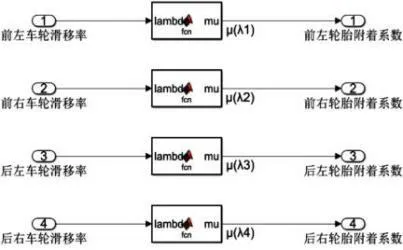
图6 魔术公式模型实现图Fig.6 Magic formula model implementation diagram

图7 和图8 分别显示了干混凝土路面和湿沥青路面下的前轮和后轮速度(轮速和车速)和滑移率变化曲线。

图7 无控制器且有控制输入的干混凝土路面仿真结果Fig.7 Simulation results of dry concrete pavement without controller and with control input

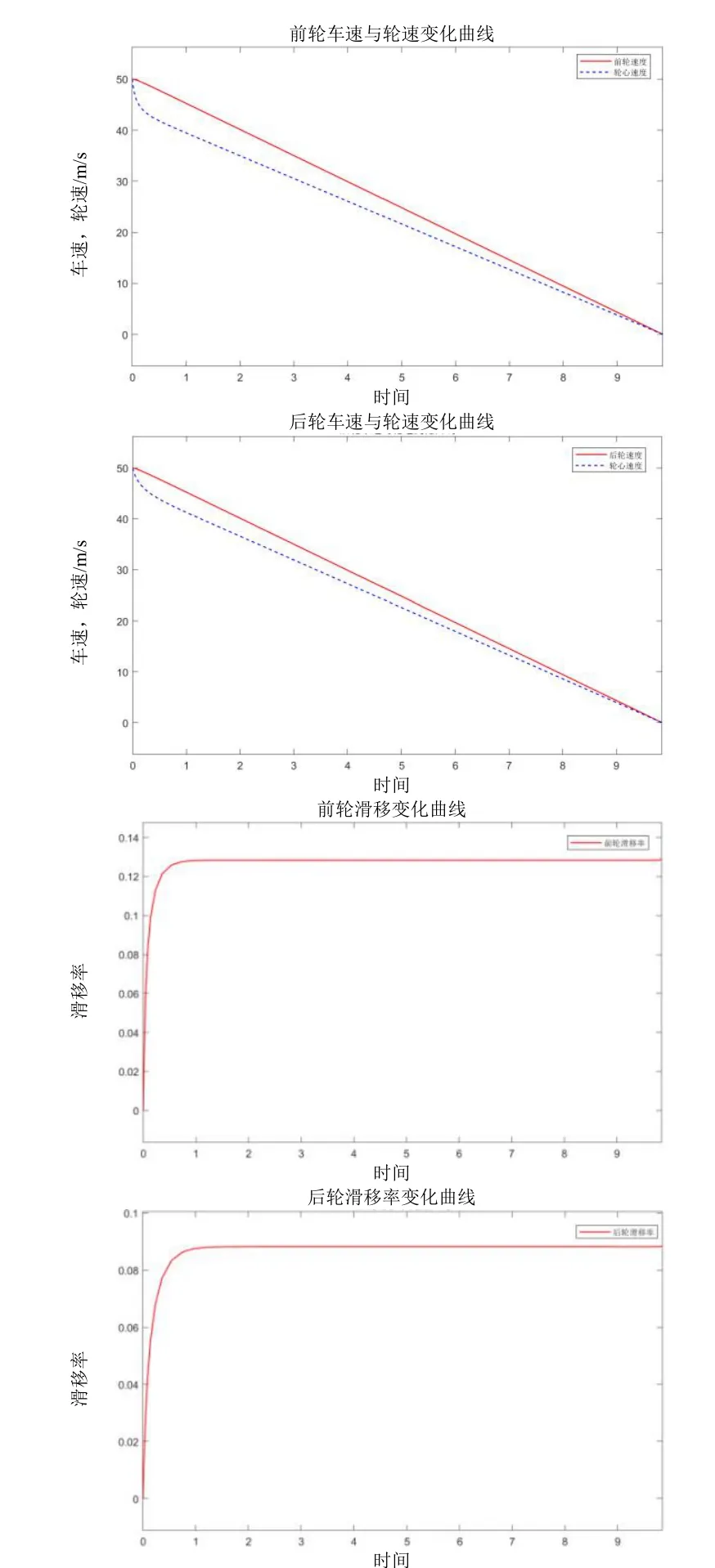
图8 无控制器且有控制输入的湿沥青路面仿真结果Fig.8 Simulation results of wet asphalt pavement without controller and with control input

根据仿真结果，可以直观地看到前后车轮速度和轮心速度都呈缓慢下降曲线，并且两者之间的差异很小，因此滑移率近似等于零。符合实际车轮制动情况。但前轮和后轮滑移率变化不一致，可能会造成车辆行驶过程中的甩尾。且从图中可以看出直观地看出，相对于干混凝土路面，在湿沥青路面进行制动，无论是制动时间还是制动距离，都大大增加。考虑到路面危险性，选择湿沥青路面环境进行控制器的验证工作。

接下来，选用传统滑模面公式(11)和传统等速趋近律公式(21)来设计滑模控制器，并在simulink中成功搭建了控制器模型如图9 所示。

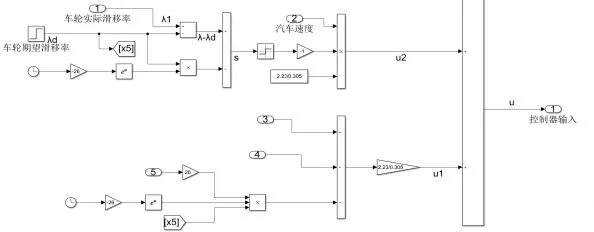
图9 传统等速趋近律滑模控制器Fig.9 Traditional constant velocity reaching law sliding mode controller

针对设计的滑模面和趋近律，给出相应参数：K=1，ε=1。仿真结果如图10 所示。

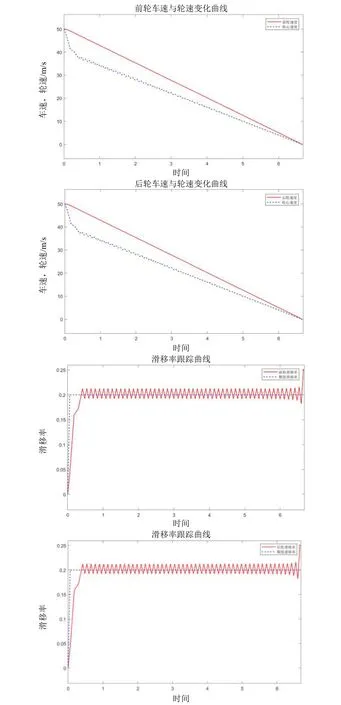
图10 传统等速趋近滑模控制器仿真结果Fig.10 Simulation results of traditional constant velocity approach sliding mode controller

从图10 可以看出，虽然传统等速趋近滑模控制器可以跟踪到期望滑移率λd，但是在期望滑移率附近产生了剧烈的抖振，并且随着时间的推移，抖振并没有减少。为了消除这种抖振，引入传统指数趋近律滑模控制器，其相关参数为：K=1，ε1=0.1，ε2=8。对其进行仿真，结果如图11 所示。

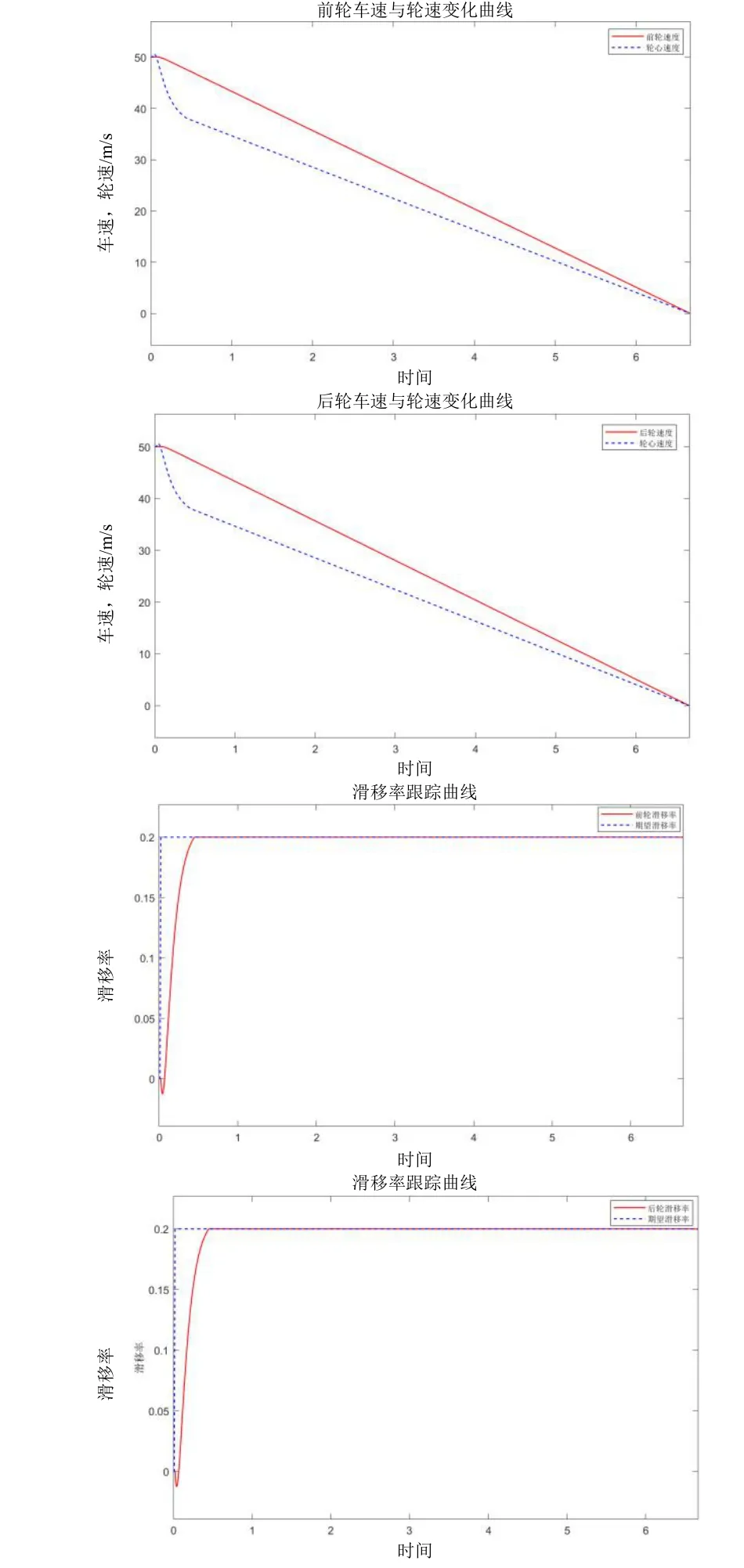
图11 传统指数趋近滑模控制器仿真结果Fig.11 Simulation results of traditional exponential approach sliding mode controller

从图11 可以看出，传统指数趋近滑模控制器可以使车轮滑移率在短时间内跟踪到0.2，并且消除了在期望滑移率附近产生的抖振，可以很好地控制车轮滑移率。制动时间并没有提升多少。通过应用新设计的全局滑模面结合传统指数趋近律进行控制，在simulink 中搭建控制器并进行仿真分析，结果如图12 所示。相关参数为：K=1，ε1=0.1，ε2=8，η=26。

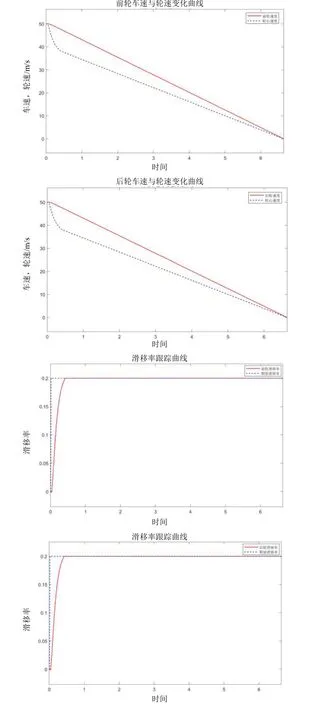
图12 传统指数趋近全局滑模控制器仿真结果Fig.12 Simulation results of traditional exponential approach global sliding mode controller

相对于传统指数趋近滑模控制器，引入全局滑模面的新控制器，减少了汽车制动时间并缩短制动距离，但是滑移率曲线不平滑，说明在趋近期望滑移率过程中稳定效果不是太好。最后，结合新的指数趋近律，设计一种新型指数趋近全局滑模控制器，相关参数为：K=1，ε1=0.1，ε2=8，η=26，α1=300，α2=50。控制器模型如图13 所示，仿真结果如图14 所示。

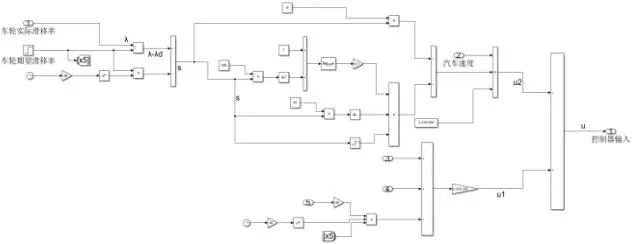
图13 新型指数趋近全局滑模控制器Fig.13 New exponential reaching global sliding mode controller

图14 新型指数趋近全局滑模控制器仿真结果Fig.14 Simulation results of a new exponential reaching global sliding mode controller

从图14 明显看出，新设计的控制器不仅能在短时间内跟踪到期望滑移率，并且在趋近过程中滑移率曲线更平滑，相对于传统指数全局滑模控制器，该系统更加稳定，具有良好的鲁棒性。同时，该方案具有较小的制动距离和制动时间，并显示出良好的制动性能。因此，与其他控制器相比，所提出的新型全局滑模控制器具有更好的性能。它非常适合于非线性防抱死制动系统。四种不同控制方法的制动距离和制动时间如表2 所示。

表2 不同控制器仿真结果比较Table 2 Comparison of simulation results of different controllers

从表2 中可以看出，在四种控制方法中，具有改进指数趋近律的全局滑模控制器具有最短制动距离和制动时间，它具有最佳的制动性能。与传统的线性滑模控制器相比，制动距离缩短了5.2 m。

4 小结

本研究针对非线性ABS 系统设计了一种新型全局滑模控制器。首先，本次研究了无控制器的干混凝土和湿沥青的ABS，考虑到汽车的初始速度分别为50 m/s，Tb1=Tb2=800 N·m，Tb3=Tb4=200 N·m。仿真结果验证了该控制策略的有效性和准确性。由于湿沥青路面下的车轮制动情况更加复杂，研究主要在湿沥青路面环境下进行仿真分析。针对滑模控制器，首先设计了一种改进的非线性全局滑模面，给出了传统的指数趋近律，以满足滑模趋近条件。其次分析了应用传统指数趋近律的非线性全局滑模控制器的控制性能。仿真结果表明，控制方案具有较好的制动性能。最后，基于传统的指数趋近律，提出了一种改进的指数趋近律。仿真结果表明，相比较传统的指数趋近律，本研究所提出的改进方案具有更好的制动性能，其车轮滑移率保持在理想的车轮滑移率附近，从而减少了抖振问题。所提出的控制方案可以获得全局鲁棒性，并可以有效地控制ABS。