基于多时间尺度Cholesky分解AEKF的锂电池SOC估计
2024-03-25徐洁玉王冬青
徐洁玉, 王冬青
(青岛大学电气工程学院, 山东 青岛 266071)
1 引言
准确估计电池的荷电状态是电动汽车合理实施电池管理的前提和重要依据,能够保证电池的良好使用性能和提高电池使用寿命[1,2]。然而,电池在实际工作过程中存在着非线性、多工况运行、多时间尺度动态等复杂特性,对锂电池的建模和估算带来了困难和挑战[3-5]。
目前主流的荷电状态(State Of Charge, SOC)识别方法有开路电压法、安时积分法、数据驱动法和基于模型估计法[6]。通常,开路电压法为其他锂电池估计方法提供初始SOC。安时积分法的优点是测量简单,但积分过程中累积的误差无法消除。数据驱动法不需要建立等效电路来描述电池行为,但是依赖数据量构建数据驱动模型[7,8]。与上述SOC估计方法相比,基于模型的估计方法可以结合多种方法进行SOC估计,具有呈现锂电池物理意义的优势。因此,基于模型方法在SOC估计领域得到普遍关注[9]。
通常,锂电池模型可分为等效电路模型、电化学模型和机器学习模型三类[10,11]。基于等效电路模型的卡尔曼滤波方法具有简单和能够在线辨识的优势,被广泛应用于锂电池SOC估计中[12,13]。扩展卡尔曼滤波(Extended Kalman Filter, EKF)是解决非线性系统问题的有效方法[14]。基于泰勒展开原理,EKF忽略了二阶和高阶项,使算法结构变得简单。然而,这种线性化方法直接忽略了高阶项,通常会引入较大的误差[15,16]。无迹卡尔曼滤波器(Unsented Kalman Filter, UKF)将系统视为黑匣子,它使用sigma点的集合来近似概率分布,并避免求解雅可比矩阵[17],但是当使用UKF算法时,误差协方差矩阵必须是正定矩阵,非正定误差协方差矩阵将在中途终止算法[18]。在传统的EKF算法中,一般假设系统噪声是恒定的高斯白噪声,然而电池系统中噪声会受环境条件等因素的影响而发生变化。因此采用自适应扩展卡尔曼滤波算法(Adaptive Extended Kalman Filter, AEKF)对噪声在线估计,实时更新系统和过程噪声的均值和误差协方差,以提高算法估算精度[19,20]。
本文在考虑锂电池成组的基础上,针对锂电池SOC估计存在的问题,以二阶等效电路模型为研究对象:①对应不同状态变量子方程,选择不同采样周期,解决不同状态变量的不同时间尺度问题;②考虑噪声变化影响,对锂离子电池SOC值自适应调节和校正,引入矩阵Cholesky分解方法,解决误差协方差矩阵非负定性问题;③为了证明本文算法的有效性和普适性,利用NEWARE锂电池测试平台获取不同型号锂电池在不同工况下的实验数据,并通过Matlab仿真进行了实验验证。
2 理论分析
2.1 等效电路模型
二阶RC等效电路模型如图1所示,其中Uoc为开路电压,R0为欧姆内阻,R1和R2为极化电阻,C1和C2为极化电容,UT为端电压,I为端电流,规定其放电方向为正,充电方向为负。

图1 锂离子电池二阶RC等效电路模型Fig.1 Second order equivalent circuit model of lithium battery
由基尔霍夫定律可知:
UT,k=Uoc,k(SOCk)-IkR0-U1,k-U2,k+vk
(1)
式中,k为采样点;vk为均值为rk、协方差为Rk的观测噪声。
R1C1和R2C2回路离散形式的全响应分别为:
(2)
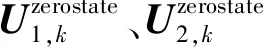
SOC采用安培小时积分法计算如下:
(3)
式中,η为充放电效率;Cn为电池的标称容量。
假设k时刻,锂电池状态变量为:
xk=[SOCkU1,kU2,k]T
(4)
由式(2)~式(4)可得锂电池状态方程为:
(5)
式中,wk-1为均值为qk-1、协方差为Qk-1的输入过程白噪声。
2.2 多时间尺度AEKF算法
对于锂电池,在充电和放电过程中,电池内部会发生不同的过程,导致不同时间尺度上的复杂动态变化,这反映在已建立的等效电路模型中不同RC环节的不同时间常数中。因此对于不同RC环节相关的不同电压状态方程采用不同的采样率。Δt1、Δt2为不同环节采样周期,利用不同环节的采样周期建立多时间尺度状态空间方程如下:
(6)
首先列出系统的多时间尺度状态和观测方程为:
xk=Akxk-1+BkIk-1+Lkwk-1
(7)
zk=UT,k=Hkxk+vk
(8)
(9)
(10)
(11)
式中,Ak为传递矩阵;Bk为系统控制矩阵;Hk为观测矩阵;∂为求导;Lk为噪声驱动单位矩阵。
自适应卡尔曼滤波算法流程如下:
(1)初始化。
(12)
(13)

(2)更新状态估计矩阵及误差协方差矩阵。
(14)
Pk,k-1=AkPk-1AkT+LkQk-1LkT
(15)

(3)更新卡尔曼增益Kk。
(16)
(4)计算残差。
(17)
(5)更新当前时刻状态估计和均方误差方程。
(18)
Pk=(F-KkHk)Pk,k-1
(19)
式中,F为单位矩阵。
(6)计算加权系数。
(20)
式中,b为遗忘因子,通常取0.95~1。

(21)
(22)

(23)
(24)
(8)返回第2步继续迭代计算,直到满足要求。
2.3 基于Cholesky分解的多时间尺度AEKF估计方法
在滤波过程中,Pk应保持非负定性,但是在计算过程中,由于计算机字长有限,存在舍入误差,Pk将失去非负定性,滤波增益出现失真,导致滤波发散。引入矩阵Cholesky分解方法可以使Pk保持非负定性,协方差分解矩阵Gk将代替误差协方差矩阵Pk进行迭代更新。
根据Pk,k-1的定义,Pk,k-1应保持正定性,即:
(25)
式中,Lk-1为下三角矩阵;Dk-1为对角矩阵,且对角元素全为正。此时若:
(26)
则

(27)
式中,Gk-1为下三角阵,是协方差分解矩阵,这种分解叫做Cholesky分解。根据卡尔曼滤波方程,一步预测方程可以进行如下变形:
(28)
其中
Gk,k-1=Ak-1Gk-1
(29)
此时可以得到k时刻误差协方差矩阵:
(30)
其中
(31)
设
(32)
则
(33)
其中
(34)
则
(35)
因此不难解得:
(36)
(37)
利用Gk可以得到Kk的表示方程:
Kk=mkGk,k-1Sk
(38)
基于Cholesky分解的多时间尺度AEKF (Cholesky-based decomposition Multi-scale AEKF,CMAEKF)算法的自适应更新方程为:
(39)
(40)
Kk=mkGk,k-1Sk
(41)
(42)
(43)
(44)
3 实验结果与讨论
为了验证本文提出算法的普适性和有效性,以锂电池NCR-18650和BTCAP-21700为实验对象,表1为不同型号锂电池具体参数,考虑电池老化等因素的影响通过降低电池容量来模拟电池老化的现象。在混合功率脉冲特性工况(Hybrid Pulse Power Characteristic, HPPC)、城市道路循环工况(Urban Dynamometer Driving Schedule, UDDS)和动态应力测试工况(Dynamic Stress Test, DST)等不同的复杂工况进行实验并与其他算法进行对比验证。

表1 电池参数Tab.1 Battery parameters
3.1 实验平台搭建
本文采用电池测试平台为新威电池测试仪NEWARE CT-4008-5V12A-TB,如图2所示。

图2 电池测试平台Fig.2 Battery test platform
3.2 模型参数在线辨识
3.2.1 开路电压与荷电状态关系标定实验
本节选用HPPC工况,采集放电数据,端电压如图3所示。

图3 HPPC端电压Fig.3 Terminal voltage under HPPC condition
结合基于最小二乘法的8次多项式拟合,得到良好的开路电压(Open Circuit Voltage, OCV)和荷电状态SOC函数关系动态拟合效果:
(45)
3.2.2 基于最小二乘算法在线参数辨识
基于最小二乘法的锂离子电池模型参数辨识算法得到了广泛的应用。本文使用该算法实现了模型参数在线识别,参数辨识结果见表2。

表2 参数辨识结果Tab.2 Identification result of the parameters
3.3 基于Cholesky分解的多时间尺度AEKF实验验证
本文选择 UDDS和DST工况下的实验数据来对四种算法进行对比仿真验证,实际SOC值是通过安培小时积分法获得的。b设置为0.96 ,小采样周期Δt1设置为1 s,大采样周期Δt2设置为20 s。
SOC1、SOC2、SOC3、SOC4分别对应安时积分法、单时间EKF算法(Single time EKF, SEKF)、单时间AEKF算法(Sigle time AEKF,SAEKF)、CMAEKF算法的SOC估计。估算误差Err1~Err3分别与SOC2~SOC4相对应。
图4为NCR-18650锂电池在UDDS和DST条件下的电压和电流变化,SOC估计结果对比和估算误差对比分别如图5和图6所示。图7为BTCAP-21700锂电池在UDDS工况下的电压和电流变化,SOC估计结果对比和估算误差对比分别如图8所示。表3和表4为所有模拟结果的平均绝对误差(Mean Absolute Error, MAE)、均方根误差(Root Mean Square Error, RMSE)和计算效率的比较。
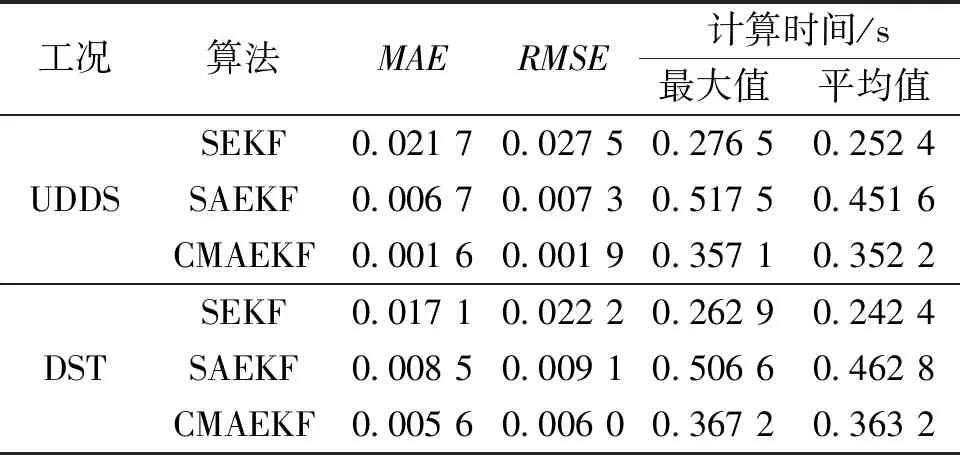
表3 NCR-18650锂电池在不同工况下不同算法结果评价Tab.3 Evaluation of different algorithm results of NCR-18650 lithium battery under different working conditions

表4 BTCAP-21700在UDDS工况下不同算法结果评价Tab.4 Evaluation of different algorithm results of BTCAP-21700 under UDDS condition

图4 不同工况下NCR-18650锂电池的电压和电流变化Fig.4 Voltage and current of NCR-18650 lithium battery

图5 NCR-18650在不同工况下SOC估计效果Fig.5 Results of NCR-18650 SOC estimation

图6 NCR-18650不同工况下SOC误差曲线Fig.6 Results of NCR-18650 SOC estimation error

图7 UDDS工况下BTCAP-21700锂电池的电压和电流变化Fig.7 Voltage and current variation of the BTCAP-21700 lithium battery under UDDS condition
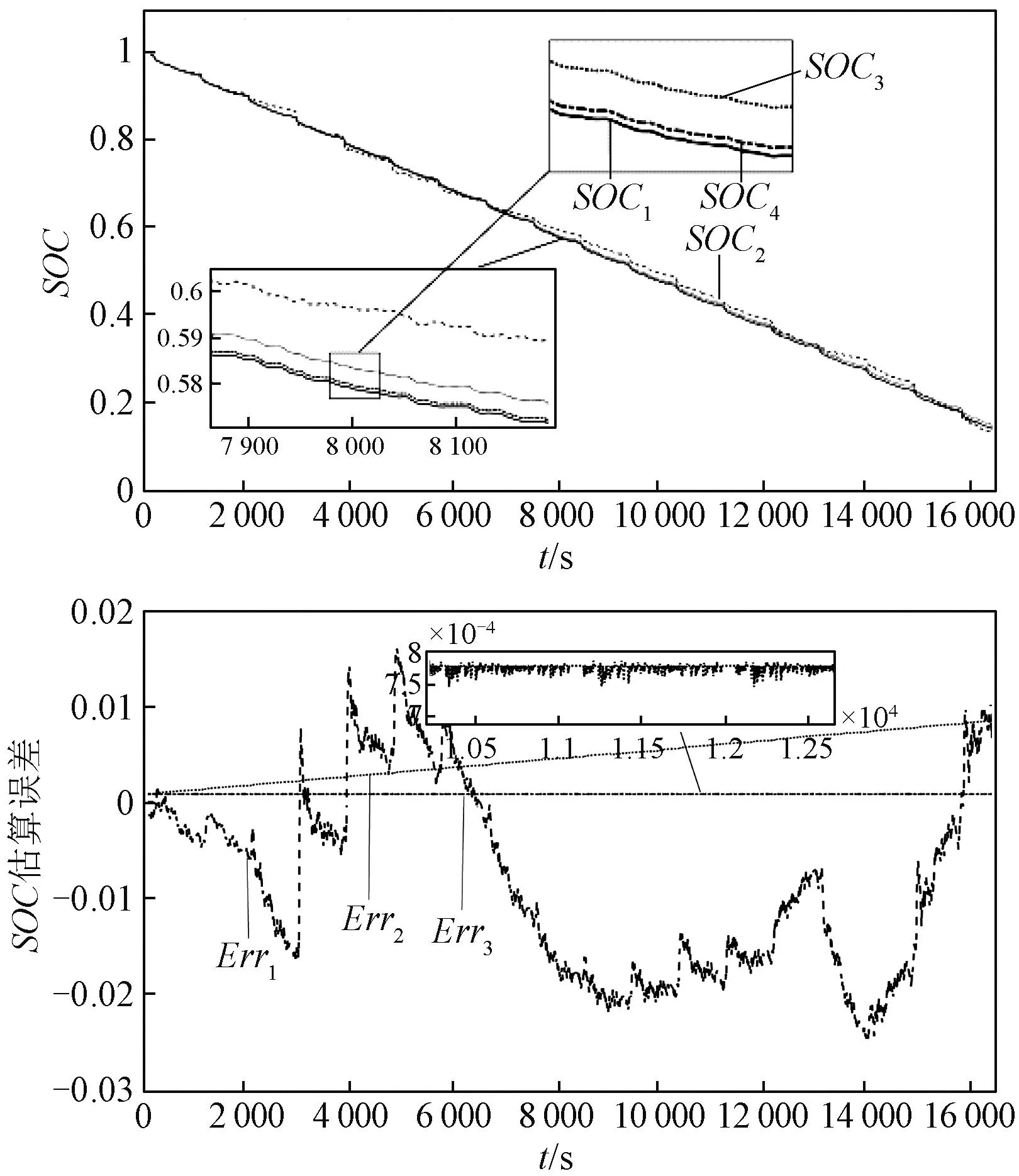
图8 UDDS工况下BTCAP-21700锂电池的SOC结果Fig.8 Results of BTCAP-21700 SOC estimation under UDDS condition
由图5、图6和图8可以看出,在放电后期,SEKF算法误差积累明显,SAEKF算法通过噪声自适应噪声矫正,可以有效地减少误差积累,基于Cholesky分解的多时间尺度AEKF算法在不同工作条件下,都具有一定的精度和稳定性,比较SAEKF算法,能更好地克服滤波发散和计算发散问题,跟踪SOC真实值变化。在表3和表4中可以看出在不同工况下,即使电池老化,CMAEKF算法的均方根误差仍然可以控制在0.6% 以下,计算效率可以比普通的AEKF算法提高至少25%。
4 结论
本文提出了一种基于Cholesky分解原理优化的多时间尺度AEKF的SOC估计方法,通过自适应卡尔曼滤波方法考虑了噪声的变化,实现了噪声的自适应矫正。结合Cholesky矩阵分解方法保证了误差协方差矩阵的非负定性,进而抑制了卡尔曼滤波器的滤波发散和计算发散。在不同工况下不同型号锂离子SOC估计上误差都在1%以下,相比传统的AEKF算法,计算效率可以提高至少25%。该算法在精度、稳定性和计算复杂度上都有明显优势。
