基于暂态响应时间分析与暂稳态模式识别的锁相环参数自适应方法
2024-03-25贾文阁杜冰心代宇琦雷万钧
于 艇, 贾文阁, 杜冰心, 孙 辉, 代宇琦, 雷万钧
(1. 深圳中广核工程设计有限公司, 广东 深圳 518000; 2. 西安交通大学电气工程学院, 陕西 西安 710049)
1 引言
锁相环(Phase-Lock Loop,PLL)通过对电网频率与相位进行检测,实现同步交流电压的功能,在交流电网中对保障电力电子并网整流器类设备正常运行起到决定性的作用。在弱电网系统中,大功率电力电子负载的切入与切除会造成系统中交流电压的幅值、相位乃至频率的突变,同时在稳态引入高于基波频率的谐波。在此应用背景下,供电暂态与稳态的运行特性分别对PLL设计有着不同的要求,对传统PLL的应用提出了挑战。
在稳态下,电力电子负载与线路阻抗共同作用,在供电电压中产生谐波。滤除谐波的抗扰需求普遍要求各形式的PLL等效频域模型具有较小的滤波带宽。现有对同步坐标系PLL(Synchronous-Reference-Frame PLL,SRF-PLL)的稳态特性研究已证明,含PLL的交直流变换器系统的小信号稳定性同样需要设计较小的PLL滤波带宽与增益[1-3]。另一方面,在暂态下,大功率的冲击负载对基波供电电压造成幅值、相位或频率突变;为保障直流负载供电质量,整流器需设计快速响应的PLL。
为平衡PLL在暂稳态中的应用需求,许多文献从改造控制方法的角度取得了进展。
一类解决方法是在PLL原有控制结构的基础上增加串行的预处理环节,滤除同步电压信号输入中的谐波[4]。常见的线性预处理环节包括静止系二阶广义积分器[5,6]及其等效的同步系带通滤波器[7,8]、陷波控制器[9,10]。非线性的预处理环节则包括如文献[11]所提出的通过正交环节提取特定次数的预处理计算,以及频率-幅值特性上等效为多频点陷波滤波器的延时预处理环节[12]。该预处理方法在不影响锁相环本身稳定性与响应速度的前提下,针对特定频点保证了滤波效果[13]。然而,此方法无法消除未纳入考虑范围的谐波频率,且多个单频点滤波器的等效串联限制了PLL的动态性能。
另一类解决方法则侧重于通过设置并行控制环路以实现多频点解耦[14],以PLL所输出的频率信号为基准,预设次数建立多个同步坐标系,分频点提取原输入信号中的各频点分量[15]。这类方法充分利用同步坐标系方法的频率特性,可以解决三相输入信号的正负序分离[16],这类方法由于谐波提取环节在响应顺序上落后于PLL,所以从输入突变暂态进入稳态的速度要更快;但在待提取频率中含有频率未知的谐波分量的工况下,按照整数次频点提取的思路不再适用,这类与基波频率挂钩的方法为了保证稳态的滤波性能,要按照高分辨率设置多个间谐波通道,大大增加了计算负担[17,18]。
为更好地设计控制方法以应对暂稳态下的不同应用需求,从理论建模方面,基于小信号线性模型,文献[1,2]分析得到结论,通过设计大带宽PLL实现高响应速度的方法对后级交变系统的稳定性存在负面影响,文献[3]进而通过引入参数自适应方法优化后级控制器稳定性。然而当PLL经历外部交流电压突变造成的暂态过程时,内部状态量不含有明确的频率特征,且工作点不固定,不满足稳态假设;当外部谐波较大时,小信号假设同样不成立。现有对PLL的分析多基于稳态小信号前提下的频域建模[19,20],难以满足对暂态响应的设计需求。近几年,基于非线性状态空间模型,文献[21,22]从暂态稳定性角度给出了估计PLL平衡点吸引域与参数稳定域的相关方法;但对暂态响应速度仍缺少分析。
针对理论分析上对大信号模型与响应速度分析的缺失,以及控制方法上对响应速度与抗扰能力均衡的不足,在现阶段对SRF-PLL稳态小信号模型研究的基础上,本文从状态方程形式的大信号模型出发,补充了对其动态响应特性的分析,并以响应时间为基准设计了PLL参数自适应框架。首先对SRF-PLL建立状态空间模型,基于该模型及动态响应过程中各内部参量的变化过程分析其动态特性;其次对PLL内部参数对响应过程的耦合作用进行分析,关注响应时间,提出对PLL分析动态特性的方法;最后依据在暂态与稳态下的不同需求设计PLL参数自适应框架,在仿真与实验中进行验证说明。
2 同步坐标系锁相环状态空间响应特性分析
SRF-PLL用于对三相输入电压信号vabc(vabc=[vavbvc]T)进行变换,通过对同步系电压vdq(vdq= [vdvq]T)进行闭环调节,获取其频率ω、相位θ输出。如图1所示为经典的SRF-PLL控制结构。图1(a)中GLPF(s)为低通滤波器(Low-Pass Filter,LPF),GPI(s)为比例积分(Proportional-Integral,PI)控制器,ω0为初始频率,θ0为初始相位,Δω与Δθ分别为其与状态量间的偏差,z-1为控制器数字实现中变量保持的一拍延迟。

图1 SRF-PLL控制示意图Fig.1 Control diagram of SRF-PLL
图1(b)为两相静止坐标系下各旋转矢量的关系,v1为输入电压矢量,设v1f、v1h分别为v1的基波、谐波分量,其中v1f的幅值为V1,基波频率为ω1;esynd、esynq分别为单位长度的直轴、交轴参考矢量。
在经典的SRF-PLL控制中,同步电压输入vabc与反馈的相位输出θ经坐标变换得到同步旋转坐标系下的直轴电压vd、交轴电压vq;其中vq作为误差量又经低通滤波器控制器滤波,由PI控制器调节得到输出频率ω;最后经积分环节生成输出相位θ。在PLL内,LPF滤波带宽设为ωLPF;PI控制器的比例系数与积分系数分别设为Kp、Ki。
如图1(b)所示,SRF-PLL内部涉及的同步旋转坐标系基于θ建立,三相同步电压在其中对应的瞬时电压矢量v1相对于参考矢量esynd的误差角为φsyn。
本文仅基于SRF-PLL的基本结构讨论PLL对基波暂态响应与稳态谐波响应特性。对于不平衡的三相同步电压及其突变暂态,由于正负序之间频率差距较小,且负序为大信号,不应作为谐波处理;而应改变PLL结构,在正序基波基础上添加文献[16]所述的正负序分量交叉提取预处理环节;对单个SRF-PLL环路,其输入仍然是三相平衡的基波大信号与谐波小信号。
在PLL调节暂态或稳态中取任一时间点,设其中经闭环反馈得到的输出频率ω与相位θ在这一时刻均为常数,则在图1(a)中由vq到θ的前向通道增益为线性传递函数模型:
(1)
该增益可以看作将输入归一化成为单位幅值的正弦波形时,θ对静止坐标系下输入频率ω1的响应。TF(s)的频率特性如图2所示。

图2 PLL开环频率响应Fig.2 Open-loop frequency domain characteristics of PLL
由图2可知,输出频率ω越接近输入频率ω1,输出相位关于输入幅值的增益普遍越大,意味着调节速度越快;且各参数与输入幅值均与增益变化趋势相关。当系统经历输入频率突变的暂态时,可以看作工作点在曲线上发生水平位移,对应的幅值增益与响应延迟随之改变。为进一步分析PLL的动态调节过程,设PLL以零初始状态启动,va、vb、vc为三相对称平衡的正弦信号,即:
(2)
经过同步坐标系变换后,得到:
(3)
则由ω1为输入,θ为输出的SRF-PLL状态空间模型可以写作:
(4)
式中,x1为LPF积分运算的中间状态量。
同样可以看出ωLPF与Ki均在局部起着增益系数的作用,而V1、Kp作为整体增益发挥作用。
基于大信号模型式(4),三相平衡幅值突变相当于调节过程中比例系数的突变,仅对系统调节速度有影响;当PLL响应过程已经进入稳态后,不会造成新的暂态或扰动。故在后续讨论中不涉及。
假设初始状态0≤ω<ω1,则根据图2与式(4),SRF-PLL从工作特性包括以下特征:
(1)当频率差ω1-ω固定为任一值时,开环输入vq为一直流分量为零的交流信号。假设其正半周使ω接近ω1,负半周使ω远离ω1,则ω将会重复接近、远离ω1的过程。由于图2所示的幅值增益显示出单调性,ω接近ω1时的开环增益大于ω远离ω1时的开环增益,故ω接近ω1的速度将会大于远离ω1的速度。
(2)在调节过程中,参数ωLPF影响ω1-ω较大时的响应增益,对应暂态下的响应速度,也对应稳态下对谐波的阻尼效果;参数Ki影响ω1-ω较大时的响应增益,对应稳态与接近稳态时的响应速度;参数Kp与输入幅值V1作为式(4)中的系数,共同决定PLL在全过程中对输入的增益与响应速度。
因此,SRF-PLL在零状态启动过渡至ω1对应的稳态过程中,会经历以下调节过程:
(1)当频率差ω1-ω较大,使图2所示的幅值增益较小时,即输出θ关于输入vq的响应小,故PLL虽然表现出ω逐渐接近ω1的趋势,但输出ω与θ变化的速度慢。
(2)当频率差ω1-ω较小时,vq的频率足够小,使得ω接近ω1的交变半周时间足够长。并且,此情况下由于图2所示的幅值增益较大,输出响应的速度足够快,ω将会在这一半周内大幅度接近ω1,过渡进入稳态。
(3)当频率差ω1-ω极小时,vq为以同步输出与实际输入间相位差决定的直流量,输出对输入的开环增益极大,在短时间内将相位差调节至零,系统可认为已进入稳态。此时高频增益作用于输入中的谐波信号,对输出造成扰动。
为详细分析暂态响应中各参数的作用效果,对PLL大信号模型式(4)改变参数,为方便表达,设输入基波角频率ω1对应的频率为f1,绘制单位幅值输入下零初始状态响应的时域响应图与在vq-ω平面上状态变量相图如图3所示。

图3 SRF-PLL不同参数作用下的零初始状态响应Fig.3 Zero-state response of SRF-PLL with different parameters
图3展示的暂态调节过程与上述分析基本一致。比较图3中不同f1的响应特性可知,输入频率作为输出ω初始状态ω0与稳态ω1间的距离,与调节时间、超调均为正相关。当ω1增加到一定程度时,由于PLL无法在第一个振荡周期令输出频率ω上升至ω1附近,需要后续更多周期进行调节,故调节时间会显著增加;与上文根据开环频率响应的调节过程分析相对应。
不同Kp的响应特性曲线印证了基于模型式(4)对响应速率的分析;类似地,滤波带宽ωLPF作为开环增益式(1)中的阻尼因素,影响系统在暂态的振荡频率。二者均与超调量、响应时间相关;响应时间骤增的规律与上文分析一致。
根据参数作用分析,可总结暂态下PLL参数设计要求:为保证PLL在特定输入信号频率下,超调量与调节时间在允许范围以内,应设计较大的ωLPF与Kp,基本与上述动态响应过程分析结果一致。
3 同步坐标系锁相环响应时间分析
为得到控制标准对参数设计的要求,需要对图3中控制过程指标与控制参数的关系总结公式。
对于式(4),应用一阶LPF的PLL模型,设输入幅值V1恒为1,PI调节器中Ki=10;ωLPF、Kp为变参数,响应时间Ttrans为研究指标。规定Ttrans的计算标准为:PLL零状态响应的输出ω在时刻t=Ttrans后总是在ω1的±1%以内。尝试对几组算例绘制响应时间与参数的关系,并根据特定的Ttrans在曲面上截得ωLPF-Kp参数曲线,得到参数关系图如图4所示。
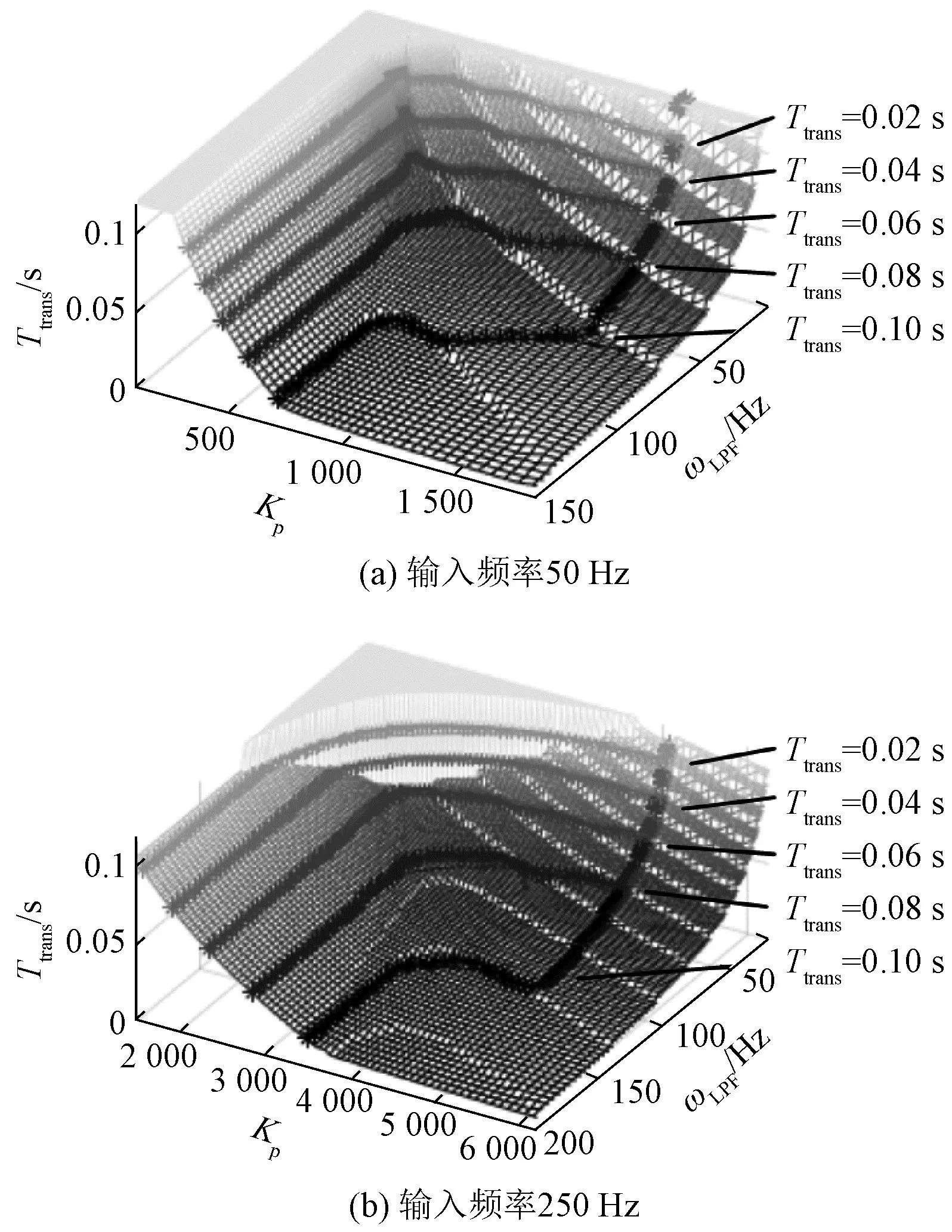
图4 响应时间与参数关系图Fig.4 Parameter-response time diagram of PLL
图4中曲面与截得曲线基本表现出以下特征:
(1)总体来说,Ttrans与ωLPF、Kp均为负相关,当ωLPF、Kp均在一定范围内时,同一Ttrans截得参数曲线为负相关的曲线。
(2)随着ωLPF增加,ωLPF对Ttrans变化影响减小,当ωLPF足够大时,LPF滤波作用不明显,参数变化对Ttrans不再有影响。
(3)随着Kp增加,Ttrans-Kp关系失去单调性。由图3可知,Kp与暂态调节过程中状态变量的振荡幅度正相关,从而造成实际Ttrans延长,解释了该现象。
上述特征描述了图4中相同的暂态响应速度对参数设计的要求;在此基础上,根据稳态下稳定性与抗扰性能对PLL带宽限制的要求,在图4中对Kp限制了最大值Kp_MAX,以优化稳态低滤波带宽时的响应性能。
图4表示出的参数与响应时间变化规律可以成为参数整定的基准。对图4中ωLPF-Kp参数曲线进行分段线性拟合,所得表达式即为状态空间模型式(4)反映的,特定响应时间要求对参数间的关系约束。在确定一预设的基波频率fnominal与响应时间Ttransref后,该参数关系式可作为参数自适应方法的基准之一。
4 同步坐标系锁相环参数自适应方法设计
对SRF-PLL稳态与暂态模型的分析表明,经滤波采入的信号幅值随时间变化,且在不同调节阶段对参数的设计有着不同需求。因此,本文采用参数自适应方法,对输入电压信号进行判断,通过输入信号检测与调节过程判断,为滤波器设定合理的参数:
(1)当调节过程处于暂态时,设计较大带宽以保证待测频率分量正常输入,并设计对应的PI增益以缩短调节时间。
(2)当调节过程接近稳态时,逐渐减小带宽以保证抗扰性能,并限制PI增益以保证闭环稳定性。
为了决定参数的更新方式,设计输入检测方法,做出PLL调节状态处于暂态或稳态的判断。
根据式(3),结合图1(b)所示的旋转矢量示意图可知,当v1h=0时,v1=v1f;PLL在暂态调节过程中,随着输出θ与实际基波相位之间的误差减小,图1(b)中同步误差角φsyn逐渐减至接近零。设φd>0为一极小的误差角,则可以认为,当∣φsyn∣ ≤φd时,系统进入稳态。当v1h≠0时,PLL即便已进入调节稳态,φsyn仍不恒为零,而是会受谐波输入的作用,在一定范围内振荡。设φs>0为∣φsyn∣在含谐波稳态下的上限值,则最大误差角为:
φv=max{φd,φs}
(5)
最大误差角可以作为自适应方法的标准,区分暂态与稳态的边界。对PLL内的状态量滤波后计算实际误差角:
(6)
当φsyn>φv时,认为PLL调节处于暂态,ωLPF应向增大方向更新,以快速跟踪同步电压目标输入;当φsyn≤φv时,认为PLL调节进入稳态,ωLPF应向减小方向更新,以抵抗谐波干扰。需要注意,若φv设计偏大,可以提高PLL稳态抗扰性能,但进入稳态前会经过较长的过渡时间;若设计偏小,则能快速进入稳态,但易将谐波干扰当作暂态,发生误动。
在实现中,为快速响应暂态,在增大ωLPF时单步更新到上限ωLPF_MAX;在暂态过渡到稳态时,为防止参数变化引起二次振荡,在减小ωLPF时应用二分法更新,逐步减小直至更新到下限ωLPF_MIN。
最后,由于式(4)所示的模型表明输入幅值V1与比例增益Kp对PLL有着同样的调节作用,需要对实际输入估计幅值,以图4所示的单位输入算例作为基准,等比例换算自适应方法计算所得的Kp。对于同步坐标系所表达的矢量的关系,本文采取:
(7)
式中,V1a为V1的估算值。计算V1的估算值V1a,以减小输入谐波与扰动对估算结果的影响。
综上所述,参数自适应方法流程图如图5所示,预设参数包括:基波频率标准fnominal及对该频率规定的响应时间Ttransref, 以及最大误差角φv。自适应方法的输出为PLL中控制参数ωLPF、Kp。

图5 锁相环参数自适应控制流程图Fig.5 PLL parameter adaptive control process
为验证所提PLL参数自适应方法的暂态与稳态性能,在仿真软件Simulink中搭建仿真模型,设置算例对比PLL在各参数设置下的响应效果。仿真参数见表1。

表1 仿真中关键参数设置Tab.1 Parameter settings in simulation
根据表1参数,在仿真中除应用自适应方法的PLL外,设置传统SRF-PLL方法作为对照,分别设置两组传统方法中参数ωLPF为自适应PLL滤波频率的上、下限,其Kp按照图4整定,以对比说明自适应参数方法的性能。设置仿真工况包括PLL输入三相电压相位突变增减π/3的暂态,频率增减1 Hz的暂态,零状态启动暂态,以及加入幅值为0.05 V的9次谐波的稳态工况。
注意到在设计中,自适应参数更新的频率设计为远低于PLL本身响应的频率,因此在输出结果中,参数自适应PLL的实际暂态调节时间应等于自适应参数更新周期与响应调节时间的加和。
由图6(a)可知,在输入电压相位突变暂态,自适应PLL可以通过快速增大滤波带宽,在暂态实现图6(b)、图6(c)所对比说明的,与传统方法中大带宽PLL所达到的相似的快速响应,其特性优于传统方法中小带宽设计;响应时间约为0.016 s,满足设计要求。随着响应进入稳态,图6(a)展示了PLL滤波带宽逐渐减小的过程。

图6 自适应PLL与传统方法比较仿真结果Fig.6 Comparative simulation results of adaptive PLL and traditional SRF-PLL
图6(b)表明,在频率突变的工况下,若突变范围较小,自适应PLL误差角未达到暂态响应阈值,因此自适应PLL响应特性类似于,且不弱于传统方法小带宽设计。
图6(c)表明,在频率突变范围较大的启动暂态工况下,自适应PLL通过暂态的参数响应,有着传统方法大滤波带宽设计的快速响应,响应时间为0.021 s,满足设计要求,暂态响应特性优于传统方法小带宽设计。
由图6(d)可知,在谐波畸变程度未达到最大误差角范围外时,不会触发暂态响应,自适应PLL在稳态实现与小带宽PLL相似的谐波衰减特性,稳态特性优于传统方法中大带宽设计。
对比仿真中各PLL输出结果可发现,相比传统方法下各类带宽设置的PLL,应用了参数自适应方法的PLL可以实现暂稳态识别与相应的参数调节,在各类情况下自动调节为最为理想的参数,综合实现最快的暂态响应速度与最好的稳态抗扰能力。
5 自适应方法控制效果实验验证
为验证理论仿真结果,基于TMS320F28379D处理器搭建实验平台如图7所示,对交流电压源所输出的三相电压信号进行PLL控制,并输出同步所得频率、相位信号至示波器观察。实验中,分别以表1所列参数实现本文提出的参数自适应PLL,并设置如仿真中传统SRF-PLL方法中大滤波带宽、小滤波带宽参数组作为对照,对比观察三组PLL在暂态与稳态的响应。测试工况包括相位突变增加π/2的暂态,频率由50 Hz突变为51 Hz的暂态,零状态启动暂态,含幅值为0.5 V的9次谐波畸变的稳态。观察PLL内部同步频率ω与输出同步相位θ的响应,实验结果如图8所示。

图7 实验平台设置Fig.7 Experimental platform
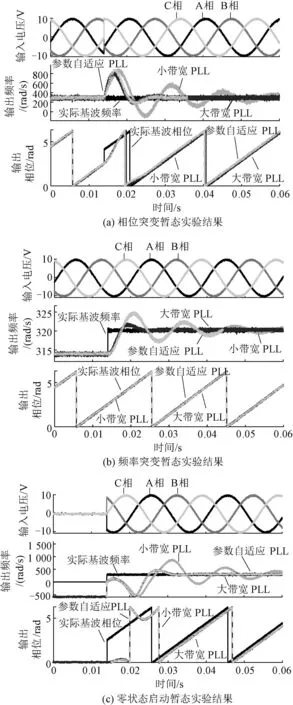
图8 自适应PLL与传统方法比较实验结果Fig.8 Comparative experiment results of adaptive PLL and traditional SRF-PLL
实验结果与自适应PLL仿真验证结果基本一致。图8(a)表明参数自适应PLL方法有着类似于传统方法大带宽设计的响应特性,响应速度优于小带宽PLL。图8(b)、图8(c)综合说明,在频率突变的暂态下,若频率变化范围小,自适应PLL方法有着不弱于小带宽PLL的响应特性;若频率变化范围大,例如在零状态启动暂态下,自适应PLL方法有着优于小带宽PLL,类似于大带宽PLL的暂态响应特性。图8(d)表明,参数自适应PLL方法在稳态的谐波扰动下有着优于传统方法大带宽设计的抗扰滤波特性。
在相位突变暂态与启动暂态下,自适应PLL均表现出了与大带宽PLL相似的快速调节特性,分别能够以0.019 s与0.020 s的实际响应时间快速进入稳态,满足设计要求。对比发现,在经历暂态后,自适应PLL既能以比传统SRF-PLL控制方法小带宽参数设计更短的调节时间快速进入稳态,避免暂态调节过程对后续输出的影响,又能够在稳态保有优于传统控制方法大带宽参数设计的谐波衰减特性,减小输出相位受输入谐波的干扰。
仿真与实验综合说明,提出的PLL参数自适应方法通过在传统的SRF-PLL结构上实现参数动态优化,综合实现了暂态快速响应与良好的稳态特性。
注意到频率突变仿真、实验结果中,参数自适应PLL的效果不是最优。这与预设相位角φsyn的设置有关。为了在较大的谐波扰动下保持稳态滤波能力,不触发对暂态的响应,自适应PLL的预设相位角φsyn设计得较小;故虽然对于相位突变能够较快识别并响应,但对于1 Hz的不明显频率突变没有进行暂态响应。
在自适应方法应用中,φsyn应当综合对PLL暂稳态性能的要求设计,令其设计范围的最小值不会使自适应系统将谐波误判为暂态,且其最大值在各类暂态工况可以保证触发快速响应,保证误差在允许范围内。
6 结论
锁相环暂态快速准确响应,稳态滤除谐波干扰的需求对应着不同的控制特性。本文结合小信号频域模型与大信号状态空间模型,分析了锁相环从暂态过渡到稳态的调节过程中内部各参数作用,在该结论基础上设计了基于响应时间分析与暂稳态模式识别的锁相环参数自适应方法。后续通过将PLL参数与后级变流器控制环节参数的稳定性设计之间建立联系,该方法所设计的PLL可以适用于弱电网中的变流器应用,应对大负载接入时造成的暂态相位、频率突变工况,接入同步暂态工况与稳态谐波干扰工况。
本文以经典的SRF-PLL控制方法为例,探讨了其参数的自适应;所提方法可以根据预设的输入频率、响应时间建立参数间函数关系,结合预设矢量误差角与实际采样输入估算锁相环在暂稳态间所处的调节状态,以逐步动态调节参数。该自适应方法也可以推广用于其他基础控制结构,并配合各类预处理环节使用。
对于后级变流器控制,所提出自适应带宽方法PLL在暂态、稳态分别呈现出带宽、增益均不同的频域特性。在检测到暂态后,随着PLL参数突变,带宽与增益增大,后级控制中需要暂时牺牲控制精度,限制后级控制器增益范围以保证稳定性,使PLL快速进入稳态;在完成电压同步,自适应PLL进入稳态后,再逐步恢复后级控制器的增益以实现稳态精确控制。
仿真与实验验证了所提参数自适应方法能综合实现暂态快速响应与稳态的抗扰特性,且在响应时间上能够满足设计要求,证明了该分析与设计方法的正确有效。
