基于阻抗分析的无刷双馈独立发电系统控制参数设计方法
2024-03-25苏婧媛杜程茂
苏婧媛, 杜程茂
(重庆大学电气工程学院, 重庆 400044)
1 引言
无刷双馈电机(Brushless Doubly-Fed Induction Generator,BDFIG)通过增添一套定子绕组等特殊结构设计,具有易变速恒频运行、仅需部分容量变换器等优点,并取消了电刷滑环等易损坏的电机结构,系统可靠性明显提升,在远航船舶、偏远山区等条件恶劣的独立发电应用中具有突出优势[1]。无刷双馈电机及其独立发电系统如图1所示。电机含有两套定子绕组,分别称为功率绕组(Power Winding, PW)和控制绕组(Control Winding, CW),具有不同极对数pp、pc以避免直接耦合,通过转子间接产生耦合影响。
PW电频率ωp、CW电频率ωc、转子机械角速度Ωm间存在式(1)所示的固有关系,根据Ωm调节ωc即可维持ωp恒定,实现变速恒频运行[2]。
ωp=(pp+pc)Ωm-ωc
(1)
目前,无刷双馈独立发电控制已有大量研究,其中基于CW电流定向的双环矢量控制策略具有动态性能好、便于限流保护等优点,是最主流的独立发电控制策略[3-5]。在此基础上针对不平衡负载[6,7]、双模式发电[8,9]等工况也已提出了拓展控制方法。以上控制策略多基于系统闭环传递函数伯德图和零极点分布情况进行控制器性能和稳定性分析,其中以电流环最为关键[2]。实际运行中,无刷双馈电机的电流环特性受电机参数、控制参数、解耦程度、转速负载等多因素影响。全面考虑以上因素会使函数阶数和复杂程度明显上升[2,4]。因此,现有研究多借助Matlab等强大的计算机工具推导电流环传递函数,直接基于复杂的推导结果利用计算机软件画出伯德图和零极点分布图,根据幅相特性和零极点分布规律指导电流环设计[4,5,9]。然而计算机工具精度及智能性有限,所得传递函数多存在零极点相消失败、阶数极高、干扰信息多等问题,不便评估系统稳定性。
针对以上电流环控制器设计遇到的挑战,本文充分借鉴双馈并网系统小信号稳定性研究常用的阻抗分析思路[10-14],提出一种基于阻抗分析的无刷双馈独立发电系统电流环参数设计方法。不同于并网发电以输出功率为控制对象,重点关注电网强度变化时的系统稳定情况[14],无刷双馈独立发电系统以输出电压的幅值频率为对象,以多变工况下高效稳定运行为首要指标,因此本文在系统建模、性能分析、参数优化等方面均与并网研究不同,具有原创性。
本文首先分别构建无刷双馈电机侧子系统小信号模型、负载侧子系统小信号模型,实现机荷信息解耦,保证模型完整性的同时降低建模复杂程度。然后基于广义奈奎斯特稳定判据分析不同转速负载工况下的系统稳定情况,指导控制参数设计与优化。最后基于64 kW无刷双馈独立运行仿真系统与实验平台验证本文分析的正确性和控制参数设计方法的有效性。
2 无刷双馈独立系统阻抗建模
2.1 阻抗分析原理
阻抗分析方法由R.D.MIDDLEBROOK于1976年提出,并广泛应用于并网系统稳定性研究[11-14]。其原理如图2(a)所示,将待研究系统拆分为源、荷两侧,源子系统用理想电压源Vs(s)和输出阻抗Zs(s)串联构成的戴维南电路描述,荷子系统用负载输入阻抗Zo(s)描述。从源侧流向荷侧的电流Is(s)可用式(2)描述。若Vs(s)、Zo(s)自身稳定,当且仅当Zs(s)/Zo(s)满足奈奎斯特稳定性判据时系统稳定。
(2)
将阻抗分析思路应用于无刷双馈独立发电系统,如图2(b)所示拆分为左侧电机子系统和右侧负载子系统,可将负载对系统的影响信息从电机侧拆分,对建模和分析起到简化作用。
2.2 电机侧阻抗子模型
2.2.1 无刷双馈电机阻抗模型
由于无刷双馈电机三相模型中电量为交流量、参数为时变量,因此基于坐标变换提出了电量均为直流量、参数为常数的统一同步坐标系dq矢量模型式(3)[15],相应等效电路图如图3所示,其中rx(下标x=p,c,r,后同)为绕组电阻;Lx为绕组自感;Lxm、Lxσ分别为绕组激磁电感、漏感;Mpr、Mcr分别为两定子绕组与转子间互感;N1、N2分别为两定子绕组与转子间匝比。式(3)中,矢量x=xd+jxq,ωr为转子电流电角频率,且有ωr=ωp-ppΩm。
(3)

图3 无刷双馈电机等效电路图Fig.3 Equivalent circuit of BDFIG
基于式(3)并忽略数值较小的rp、rr[16,17]推导各绕组电压与电流间的阻抗关系,可以得到PW、CW、转子的小信号模型分别如式(4)~式(6)所示,其中上标“~”代表小信号扰动,传递函数G1(s)~G4(s)在式(7)中给出。
(4)
(5)
(6)
(7)
定义式(4)~式(6)中传递函数矩阵为Gpp(s)、Gcc(s)、Gpr(s)、Gcr(s),系数矩阵为Grp、Grc,并以uc、ip为输入、ic、up为输出,结合式(4)~式(6)即可得到无刷双馈电机阻抗模型如下:
(8)
图4展示了电机阻抗模型式(8)描述的信号流关系,可以看到转子电流起到了耦合PW、CW以实现能量和控制传递的作用。与有刷双馈电机阻抗模型相比[18,19],无刷双馈电机阻抗模型耦合更多、形式更复杂。

图4 无刷双馈电机阻抗模型Fig.4 BDFIG impedance model
2.2.2 电流环控制器阻抗模型


图5 基于CW电流定向的无刷双馈独立运行双环控制系统Fig.5 Stand-alone BDFIG dual-loop control system based on CW-current orientation
该系统中,电流内环性能最为关键[2],需基于无刷双馈电机dq模型式(3)进行分析设计。基于式(3)第三条转子方程并同理忽略影响较小的rr,可得到ir表达式为:
(9)
将式(9)代入无刷双馈电机dq模型式(3)第二条CW方程,即可得到无刷双馈电机内部CW电压电流联系如下:
uc=(rc+Lces)ic-jLceωcic-Mesip+jωcMeip
(10)
式中,Lce、Me为集成电感,Lce=Lc-Mcr2/Lr,Me=MprMcr/Lr。
根据式(10)即可设计PI控制器及前馈补偿环节[5,16],但考虑到前馈补偿含有纯微分项,实际应用中可能引入不稳定因素;此外若前馈系数与Lce、Me偏差较大也可能影响系统稳定性。因此本文电流内环采用无前馈补偿的纯PI环节式(11),其中kp、ki分别为比例系数、积分系数。
(11)
(12)
2.2.3 电机侧阻抗子模型
联立式(8)、式(12)即可得到电流环控制下无刷双馈电机内部信号流如图6所示。
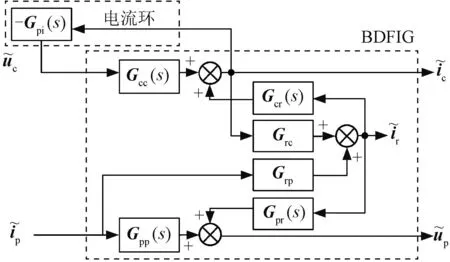
图6 无刷双馈电机侧子系统阻抗模型Fig.6 BDFIG-side subsystem impedance model
可得无刷双馈电机侧阻抗子模型ZBDFIG(s)为:
(13)
式中
Ga(s)=E+Gcc(s)Gpi(s)-Gcr(s)Grc
(14)
2.3 负载侧阻抗子模型
无刷双馈独立发电系统的负载侧电流关系如图7所示,其中iRo、iLo分别为流经并联负载Ro、Lo的有功电流、无功电流,ipP、ipQ和ilP、ilQ分别为PW电流和变换器电流的有功电流、无功电流分量。
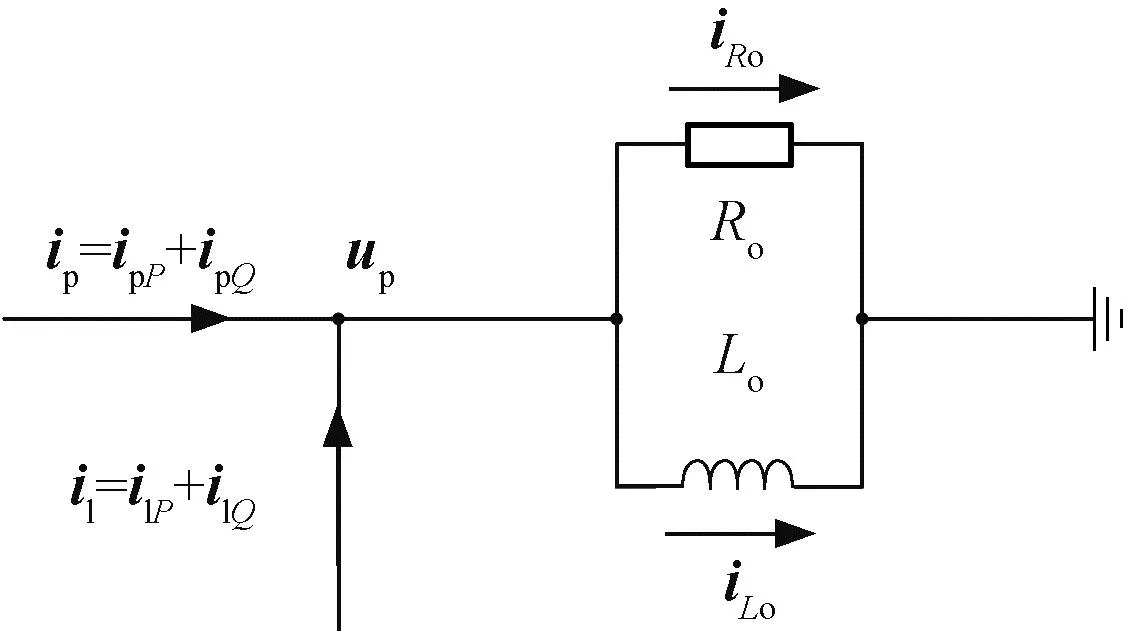
图7 无刷双馈独立发电系统负载电流示意图Fig.7 Current relation of BDFIG system
up与iRo、iLo存在如下关系:
up=RoiRo=Lo(s+jωp)iLo
(15)
此外各有功、无功电流分别存在关系如下:
(16)
考虑到电机的双馈特性,ipP、ilP间还存在转差sP倍关系,此外负载侧变换器通常会提供部分无功补偿,因此iLo、ilQ间存在无功补偿系数kQ倍关系:
(17)
联立式(15)~式(17),最终可以得到PW端up、ip间等效负载关系如下:
(18)
定义从PW端口“看到”的等效阻性负载Roe=Ro(1+sP)、等效感性负载Loe=Lo/(1-kQ),根据式(18)即可得到考虑转差功率、无功补偿影响的负载侧导纳子模型Yo(s)如式(19)所示,其中Yd(s)、Yq(s)在式(20)中给出:
(19)
(20)
后文即可基于电机侧阻抗模型式(13)、负载侧导纳模型式(19)进行控制参数设计与稳定性分析。
3 基于阻抗分析的控制参数设计
根据ZBDFIG(s)、Yo(s)可知,dq坐标系下无刷双馈独立发电系统是一个多输入多输出系统,因此可根据广义奈奎斯特稳定性判据[17]。根据式(2)得到回比矩阵L(s)如式(21)所示:
(21)
式中
(22)
系统稳定的充要条件是L(s)所有特征值的奈奎斯特曲线逆时针环绕(-1,j0)的总次数为0,因此根据式(22)解得L(s)的两个特征根λ1,2为:
λ1,2=Ld(s)±jLq(s)
(23)
以一台64 kW绕线式无刷双馈电机为例(pp=2、pc=4,转速范围500(1±30%) r/min,dq参数见表1)[20],给出无刷双馈独立发电控制系统中的关键电流环PI参数kp、ki设计方法。

表1 64 kW无刷双馈电机参数Tab.1 Parameters of 64 kW BDFIG
3.1 电流环参数设计
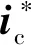
(24)
根据式(24)即可设计得到初始PI参数kp0=4、ki0=10,相应理想闭环带宽ωb=83 rad/s。由于无前馈补偿,实际带宽将小于ωb,但考虑到无刷双馈独立系统内环带宽一般在30 rad/s左右[21],因此即使实际带宽会减小,kp0、ki0仍可满足需求。
3.2 全工况稳定性评估与参数优化
虽然无前馈环节避免了微分项计算,一定程度上可提升实际系统稳定性,但增大PI参数可能带来新的稳定性风险,需进行全工况稳定性评估。
针对该64 kW电机,考虑到转速350 r/min时Roe=0.7Ro最小、输出有功功率最大,不采取无功补偿时Loe=Lo最小、输出无功功率最大,因此以350 r/min、80 kV·A满载(功率因数0.8)、不采取无功补偿为典型工况,基于式(23)得到不同转速下的奈奎斯特曲线如图8所示。
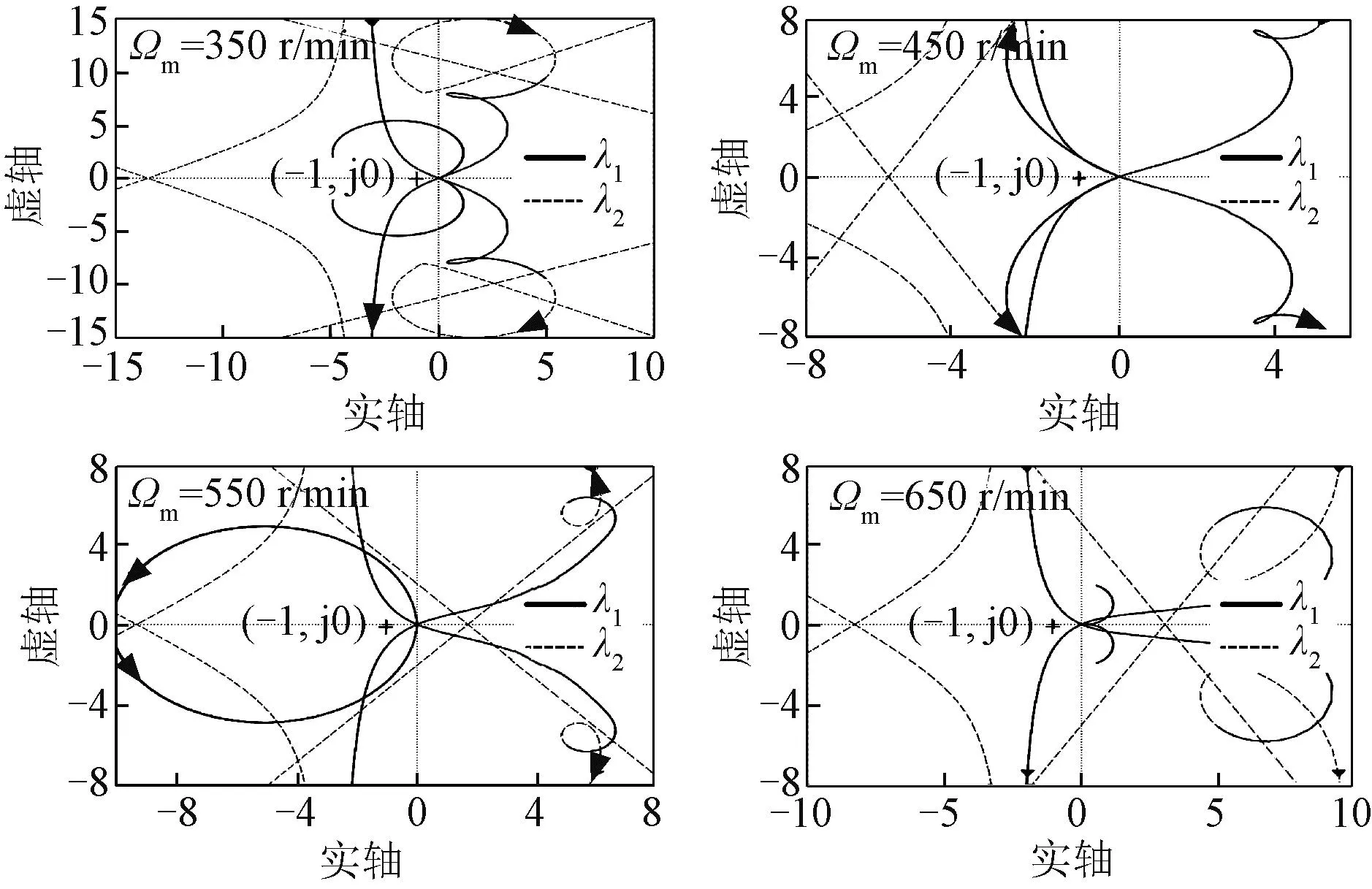
图8 kp0=4、ki0=10满载工况奈奎斯特曲线Fig.8 Nyquist curves under kp0=4, ki0=10 full-load condition
受无刷双馈电机模型复杂、Matlab符号运算精度有限等影响,所得Ld(s)、Lq(s)阶数较高、仍含有重叠零极点,奈奎斯特曲线半径较大,故图8重点展示靠近(-1,j0)的曲线细节。虽然曲线形式较复杂,但不影响分析点(-1,j0)被包围情况。
为进行直观对比,此处同时给出相同工况下的闭环传递函数分析过程,以论证本文所提方法的优势。由于闭环传递函数反映无刷双馈电机内部电量的固有关系,本质上亦为电量间阻抗特性;同时为保证不同转速负载下性能均较理想,需要将各约束信息全部代入推导过程。因此首先联立阻抗关系式(4)~式(6)、电机负载关系式(18),得到ip与ic关系如下:
ip=[Yo(s)-Gpp(s)-Gpr(s)Grp]-1Gpr(s)Grc(s)ic
(25)
进一步地,联立式(25)与电流环控制器式(11),即可得到考虑控制、负载影响后的控制绕组uc、ic闭环关系如式(26)所示,其中Gclose(s)为闭环函数矩阵,中间矩阵GC(s)在式(27)中给出。
(26)
(27)
理论上基于式(26)即可绘制Gclose(s)零极点分布图进行控制性能分析和稳定性评估。然而,由于推导一次性代入了电流环、负载约束等大量信息,如图9所示,仅Matlab所绘中间函数矩阵GC(s)(其中直接传递函数GCd(s)、耦合传递函数GCq(s))零极点已多达74个。若进一步运算Gclose(s)零极点情况,Matlab会由于过度复杂而报错。因此,若无人工干预简化传递函数,难以利用Matlab闭环主导零极点等信息从而判断系统稳定情况。对比图8、图9可以看出,本文所提阻抗分析法评估控制参数时可最大程度地发挥计算机工具的智能运算优势,无需人工简化即可获得关键的稳定性评估结果。
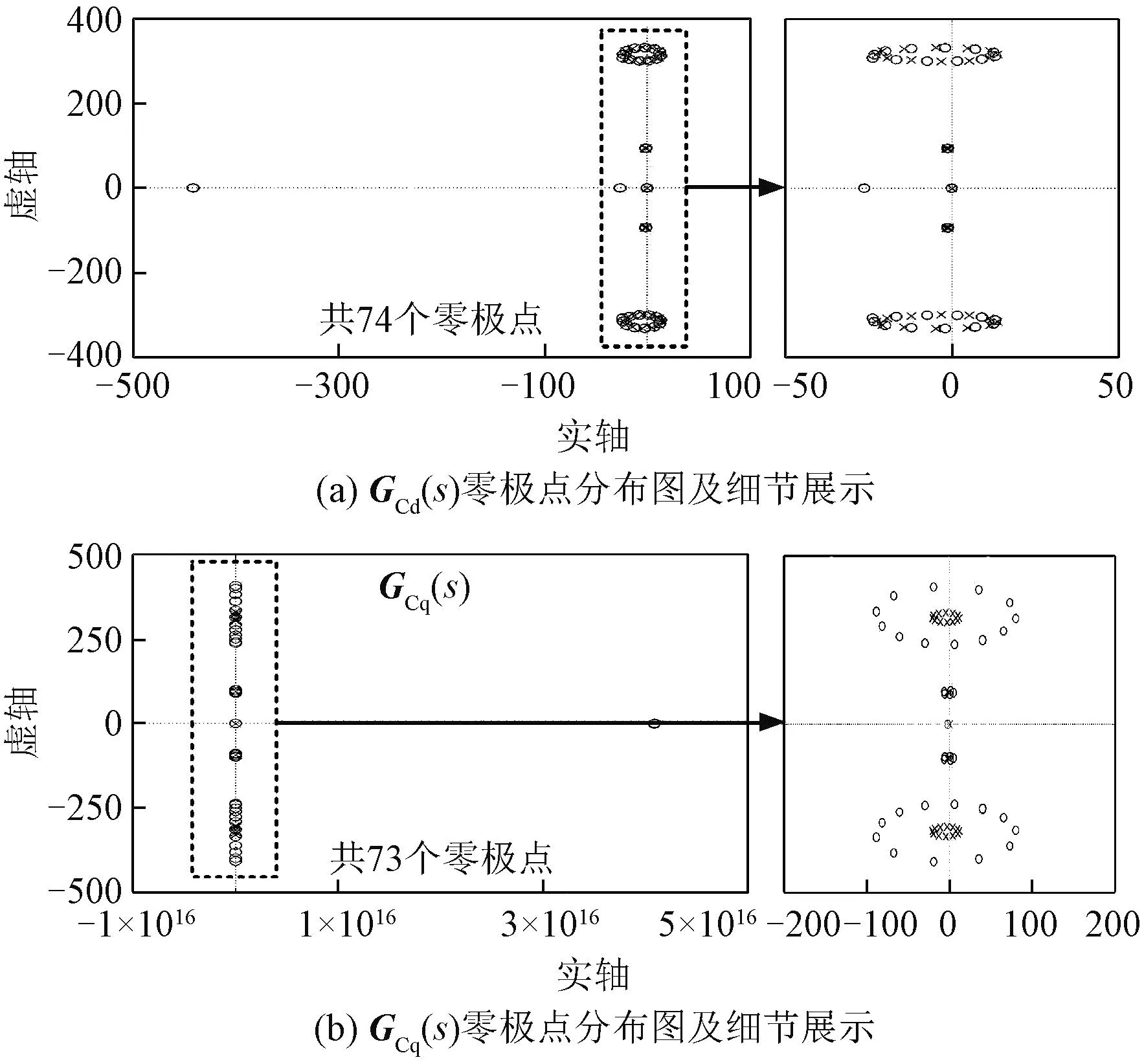
图9 kp0=4、ki0=10满载工况GC(s)零极点分布图Fig.9 Zeros and poles of GC(s) under kp0=4, ki0=10 and full-load condition
进一步地,根据图8可知kp0=4、ki0=10时,350 r/min、450 r/min、650 r/min满载工况下(-1,j0)均没有被曲线包围,系统可保持稳定;而550 r/min时λ1逆时针包围(-1,j0),系统不稳定。因此有必要对电流环PI参数进行优化。重新基于式(24)优化得到kp=4、ki=8,理想闭环带宽为ωb=80 rad/s,与优化前相近,对动态性能影响不大。与图8同理,在不同转速、负载、无功补偿程度下评估此时的系统稳定情况。如图10(a)所示,80 kV·A满载、不采取无功补偿时,各转速下的奈奎斯特曲线均不包围(-1,j0),系统可稳定运行。同理分析图10(b)可知,350 r/min下空载、半载工况时系统均可保持稳定,且结合图10(a)第一幅图,根据奈奎斯特曲线和(-1,j0)的距离可知,半载下系统稳定裕度较空载和满载更好。分析图10(c)可知,350 r/min、80 kV·A满载工况下,采取80%无功补偿、100%无功补偿时系统均可保持稳定,且同理结合图10(a)第一幅图可知,采取无功补偿后系统的稳定裕度较无补偿时更好。

图10 优化PI参数后不同工况奈奎斯特曲线Fig.10 Nyquist curves under different operation conditions after PI parameter optimization
综上,为兼顾实际应用和工况变化稳定性,本文采用无前馈补偿的纯PI电流内环控制器,并通过略增大PI参数kp、ki以弥补电量耦合导致实际带宽偏小的影响;基于广义奈奎斯特曲线和阻抗分析评估和优化kp、ki,保证各工况下系统均能稳定运行。
4 仿真实验验证
4.1 仿真验证

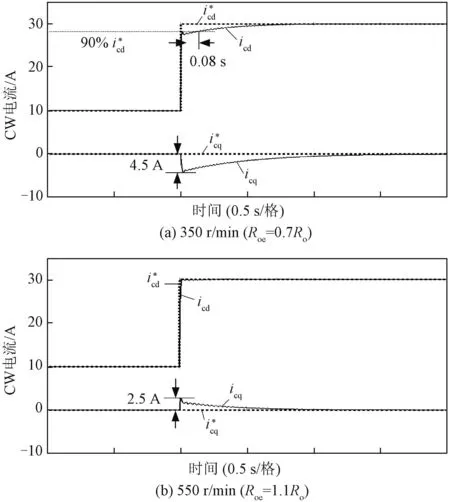
图11 无刷双馈仿真系统电流环控制性能Fig.11 Current-loop control performance of BDFIG simulation system


图12 无刷双馈仿真系统电压环控制性能Fig.12 Voltage-loop performance of BDFIG simulation system
4.2 实验验证
进一步地,将图12中所用控制参数应用于图13所示的64 kW无刷双馈独立发电系统。具体系统参数见表2。

表2 64 kW无刷双馈实验平台参数Tab.2 Parameters of 64 kW BDFIG prototype

图13 64 kW无刷双馈独立发电实验平台Fig.13 64 kW BDFIG stand-alone generation prototype
5 结论
针对无刷双馈独立发电系统控制参数设计常用闭环传递函数分析法受系统模型阶数高、形式复杂影响,人工推导工作量大,利用计算机工具分析则存在大量干扰信息,不便于评估定系统稳定性的问题,本文提出一种基于阻抗分析的无刷双馈独立发电系统电流环参数设计方法。采用较大kp、ki的纯PI电流环控制器,在提升控制可靠性的同时弥补耦合导致的带宽减小影响,并基于广义奈奎斯特曲线优化kp、ki,保证各转速负载工况下系统均能稳定运行。
本文所提控制参数设计方法不受阻抗模型复杂程度及重叠零极点影响,可直观评估系统稳定情况,无需人工简化干预。但该方法推导所得阻抗模型表达式仍较复杂,无法从模型本身获得解析形式清晰、物理意义明确的稳定性影响规律。后续研究将进一步探索更简洁直观的稳定性分析工具,并明确状态空间法、闭环函数法、阻抗分析法等各类稳定性研究方法在无刷双馈发电领域的优势和适用范围。
