利用等效复磁导率幅值对硅钢叠片铁心的改进均质化方法

张天淼, 李 琳

(新能源电力系统国家重点实验室(华北电力大学), 北京 102206)

1 引言

作为输变电路中的重要组成部分,大型变压器中常采用多层薄叠片以及绝缘涂层来抑制涡流,减少涡流损耗,以此提升变压器运行的安全性、可靠性和经济性[1-4]。在变压器有限元仿真中,多层薄叠片的直接求解存在网格剖分数多、矩阵方程维数高、内存消耗大、计算时间长等问题。商用工作站在CPU、内存、拓展性等方面相较于以往的台式机有着质的飞跃,特别适合于图像处理、工程计算等领域。但是实际大型电力装备的物理尺度可以达到数米,而其中叠片铁心的厚度只有0.3 mm或更薄,有限元剖分的单元和节点数量会非常大,对计算机内存和计算时间需求会非常高,导致无法在实际的工程设计中使用。因此通过算法上的改进,进一步减小仿真对计算机内存占用并节约计算时间,对于提高工程设计人员的工作效率至关重要。

目前,均质化方法能大幅降低有限元剖分单元数量、减少计算成本,广泛应用于实际工程仿真中。日本的五十岚等人针对多匝线圈提出均质化方法[5-8],但是所提公式涉及参数较多且不适用于软磁材料;文献[9]针对柱形和球形铁磁性夹杂物构成的周期性软磁材料晶胞提出了均质化方法,该方法能够准确描述低体积分数的软磁材料;文献[10,11]提出了适用于高体积分数的矩形铁磁性夹杂物的软磁复合材料的均质化方法,同时利用复磁导率提出一种涡流损耗的预测模型,但是该预测模型无法推广至非线性材料。上述文献仅适用于软磁复合材料(Soft Magnetic Composites, SMC),其参数取值并不适合包含硅钢片在内的软磁合金。硅钢叠片铁心的均质化方法分为磁导率的均质化方法以及电导率的均质化方法。对于磁导率的均质化方法,文献[12]从叠片与片间气隙构成的磁阻回路出发,推导出适用于叠片铁心的磁导率均质化公式。文献[12]指出,对垂直于叠压方向的磁导率做均质化处理时,叠片与气隙构成磁阻并联关系,利用磁阻并联定理求取等效后的均质化磁导率;平行于叠压方向的磁导率做均质化处理时,叠片与片间气隙构成磁阻串联关系,相应的等效磁导率可以利用磁阻串联定理求取。文献[13]给出了叠片铁心均质化后,沿垂直于叠压方向和平行于叠压方向的等效集肤深度公式,并将该公式应用于解决叠片铁心的三维涡流问题。文献[14]结合文献[13]提出的等效集肤深度公式,将其应用于电抗器铁心的均质化建模。电导率的均质化方法多种多样,主要区别在于叠压方向的电导率均质化方法,第一种方法是忽略叠压方向的绝缘涂层,用同一个公式表示垂直于叠压方向和平行于叠压方向的等效电导率[15];第二种方法考虑叠压方向绝缘涂层的存在,将平行于叠压方向的等效电导率公式与垂直于叠压方向的等效电导率公式作区分,形成各向异性均质化电导率公式[16-23]。在第二种方法中,分为直接视叠压方向电导率为零[16,17]和给定一个很小的数值两种方法[18-23]。其中,文献[18]公式及模型复杂、待测量参数较多且在非线性情况下难以使用。王坚等人[19]提出的公式简洁清晰,并在文献[20]中将其应用于TEAM Problem 21的磁通求解上;周利军等人[21]基于文献[19]提出了一种适用于卷铁心的等效厚度均质化方法;此外,还有学者针对片间短路[22]以及多点接地故障[23]提出了相应的电导率均质化方法。由于均质化后材料等效厚度增加,文献[19-23]均要利用等效集肤深度公式对边缘处作较细的网格剖分,虽然较未均质化时计算成本大幅下降,但是仍然需要占用较高的内存容量和较长的计算时间,存在进一步改进的地方。

针对当前硅钢叠片铁心均质化中计算内存消耗仍然较高、计算时间仍然较长的问题,本文以国际TEAM Problem 21 基准族中的21d-M(以下简称TEAM P21d-M)为分析对象,利用等效复磁导率幅值改进原有的均质化公式,对20层型号为30RGH120的取向硅钢片进行建模,将计算结果与实验测量值进行对比,验证了改进均质化的计算准确性。在此基础上对比未均质化、传统均质化以及改进均质化方法的剖分单元数、内存消耗和计算时间,验证了改进均质化的高效性。

2 磁场方程

2.1 三维涡流场方程

采用A,φ-A法并引入库伦规范后,在涡流区的电磁场方程为[24]:

(1)

在非涡流区的电磁场方程为:

(2)

式中,A为矢量磁位;φ为标量电位;Js为源电流密度,A/m2,在变压器中,Js可分为高压绕组电流密度以及低压绕组电流密度[25];μ为磁导率;σ为电导率,S/m。当材料为各向异性时,μ和σ将以对角阵的形式给出:

(3)

(4)

式中,x、y、z为坐标轴的三个方向。

2.2 损耗分离方法

叠片铁心总损耗可分为磁滞损耗、涡流损耗以及剩余损耗。磁滞损耗与材料内部磁畴的运动有关[26];涡流损耗取决于材料的性质、排列方式以及厚度,其中材料厚度是最重要的[27]。损耗分离公式如下所示[28]:

(5)

式中,Ptot为总损耗;Phys、Pclass、Pexc分别为磁滞损耗、涡流损耗以及剩余损耗;khys、kclass、kexc分别为磁滞损耗系数、涡流损耗系数及剩余损耗系数;Bp为磁通密度峰值;m为一个常数;f为频率。

两边同时除以频率f,并令:

(6)

可得:

(7)

在给定磁通密度下测量频率和总损耗值,并用式(7)进行损耗分离的方法称为外推法损耗分离。

3 改进的均质化公式与损耗计算

3.1 等效复磁导率

由于材料的磁滞特性,磁通密度B与磁场强度H之间存在时间滞后。为了分析磁心中的这些现象,可以将材料的相对磁导率视为复数μr=μ′r-jμ″r,其中μ′r和μ″r是频率f的实函数。以图1为例,其x方向的等效复磁导率可以通过下式获得[29]:

(8)

图1 外施磁场下的叠片示意图Fig.1 Schematic of lamination under external applied magnetic field

式中,d0为叠片厚度的一半,d0=d/2;为传播常数,与集肤深度相关,表达式如下:

(9)

式中,j为虚数单位。选取一个3%SiFe晶粒取向硅钢片,厚度为0.3 mm;电导率为2.17×106S/m;当磁通密度为1.5 T时沿x方向的相对磁导率μx=3.13×104。通过式(9)计算其各频率下的复磁导率实部与虚部的结果如图2所示[30]。

图2 复磁导率实部与虚部随频率变化图Fig.2 Real and imaginary parts of complex permeability change with frequency

3.2 考虑等效复磁导率的改进均质化公式

对于图3所示的总厚度为D0、叠片宽度为D、单个叠片厚度为d的硅钢叠片铁心模型,准确地对叠片和片间气隙进行有限元建模会产生大量剖分单元,计算成本极大。为了在降低计算成本的同时保证计算准确度,需要进行均质化处理。

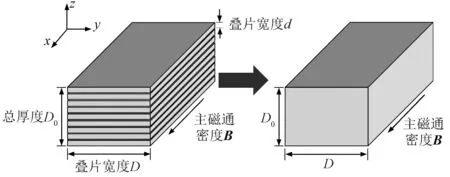
图3 叠片铁心均质化示意图Fig.3 Schematic diagram of homogenization of laminated core

设轧制方向以及切向方向的磁导率分别为μr和μt;空气磁导率为μ0;叠片系数为F,那么式(3)和式(4)中的各变量表达式为:

(10)

(11)

在使用式(10)、式(11)进行均质化时应当考虑集肤深度,均质化后的等效集肤深度公式如下所示[13]:

(12)

式中,ω为角频率;δpar为平行于叠片的平面所对应的等效集肤深度;δver为垂直于叠片的平面所对应的等效集肤深度。

综上,传统均质化分为两大步。首先利用式(10)和式(11)将多层叠片等效为一个整体;然后利用式(12)计算出等效集肤深度,加密边缘网格剖分。为了进一步降低网格剖分数目,简化计算过程,将式(8)引入,对均质化公式进行改进,得:

(13)

式中,‖·‖为取幅值。通过上述改进,可直接对整体进行网格剖分,不用为集肤效应划分额外的剖分区域。改进均质化的示意图如图4所示,自左向右分别代表非均质化、传统均质化以及改进均质化的网格剖分。

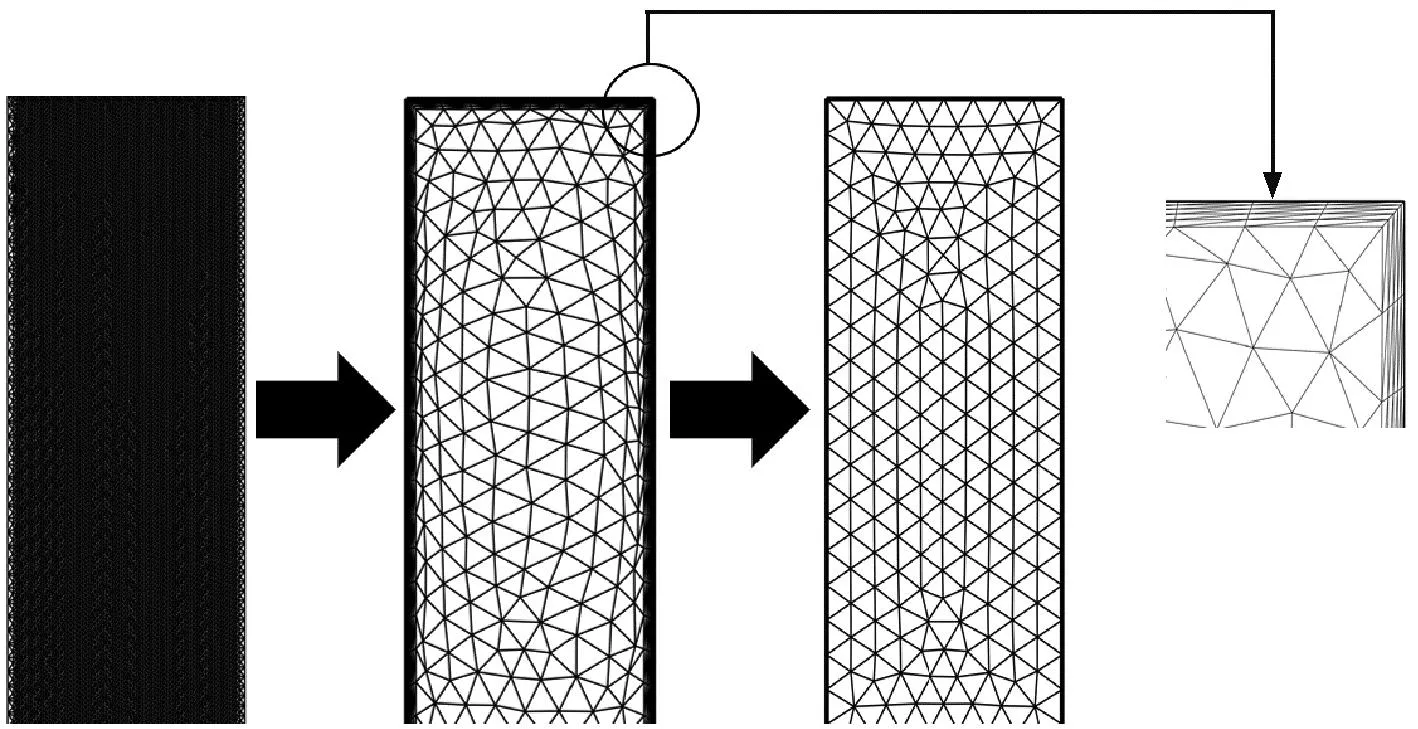
图4 改进均质化的网格剖分对比图Fig.4 Comparison diagram of mesh generation with improved homogenization

以图3所示的x方向为例,改进均质化流程图如图5所示,其中Hi为第i个H取样点,Hmax为最大的H取样点。

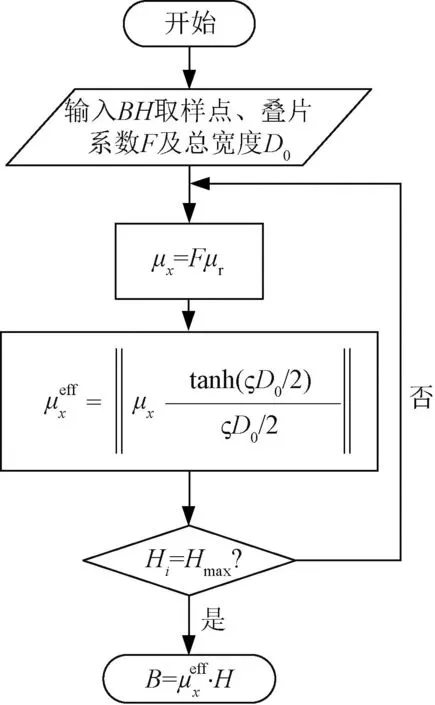
图5 改进均质化计算流程图Fig.5 Flow chart of improved homogenization calculation

取10片型号为30RGH120的硅钢片,设叠片系数F=0.955,则未均质化、传统均质化以及改进均质化后的切向方向的B-H曲线如图6所示。

图6 均质化处理对比图Fig.6 Comparison of homogenization method

3.3 剖分单元的损耗分离

磁滞损耗与磁通密度峰值的对应关系可以通过实验测量得到[31]。效仿式(7),令:

(14)

推导出如下所示的以磁通密度峰值为自变量的外推法损耗分离公式为:

(15)

总损耗表达式为:

(16)

三维有限元中一般以剖分单元重心处的Bp近似替代剖分单元内的磁通密度峰值[32]。整个硅钢叠片铁心的磁滞损耗、涡流损耗、剩余损耗及总损耗均可由下式表达为:

(17)

式中,n为剖分单元总数;Pi为第i个剖分单元的损耗;Bi为第i个剖分单元重心处磁通密度峰值;ρ为材料密度;Vi为第i个剖分单元的体积。

4 算例分析

4.1 国际基准问题模型与预处理

国际TEAM问题作为验证电磁分析方法的基准,自20世纪80年代以来发展迅速。其中,TEAM Problem 21以电力变压器为直接工程背景[31],为了探究取向硅钢叠片的非线性三维涡流问题,采用国际TEAM P21d-M,该算例含有20个型号为30RGH120的取向硅钢片,如图7所示。

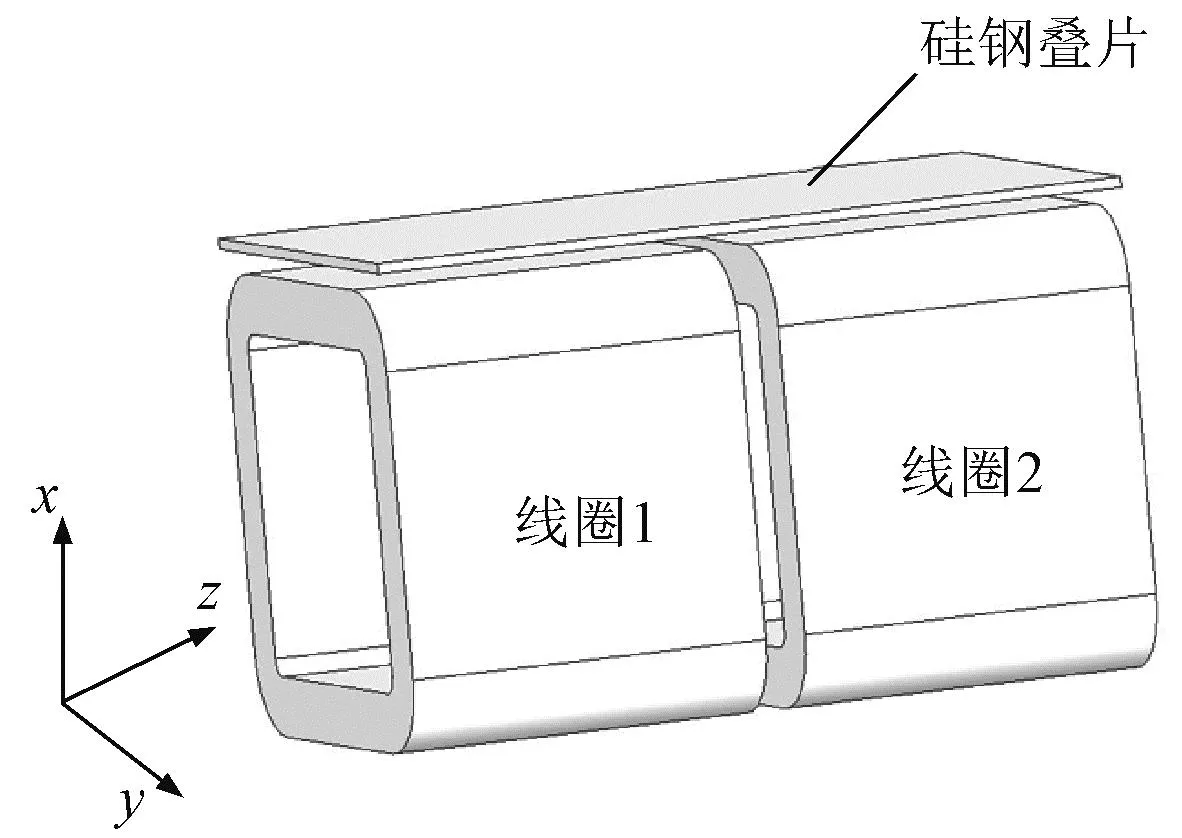
图7 TEAM P21d-M模型示意图Fig.7 Schematic diagram of TEAM P21d-M

TEAM P21d-M因线圈1和线圈2的激励方向不同,可分为反向激励、同向激励与单激励三种激励,取向硅钢片的相关数据可从文献[33]中查阅。利用式(15)对取向硅钢片的涡流损耗及剩余损耗进行拟合,拟合曲线的决定系数为0.986 6,拟合关系较好;拟合曲线与实验测量值的对比结果如图8所示。拟合曲线表达式为:

(18)

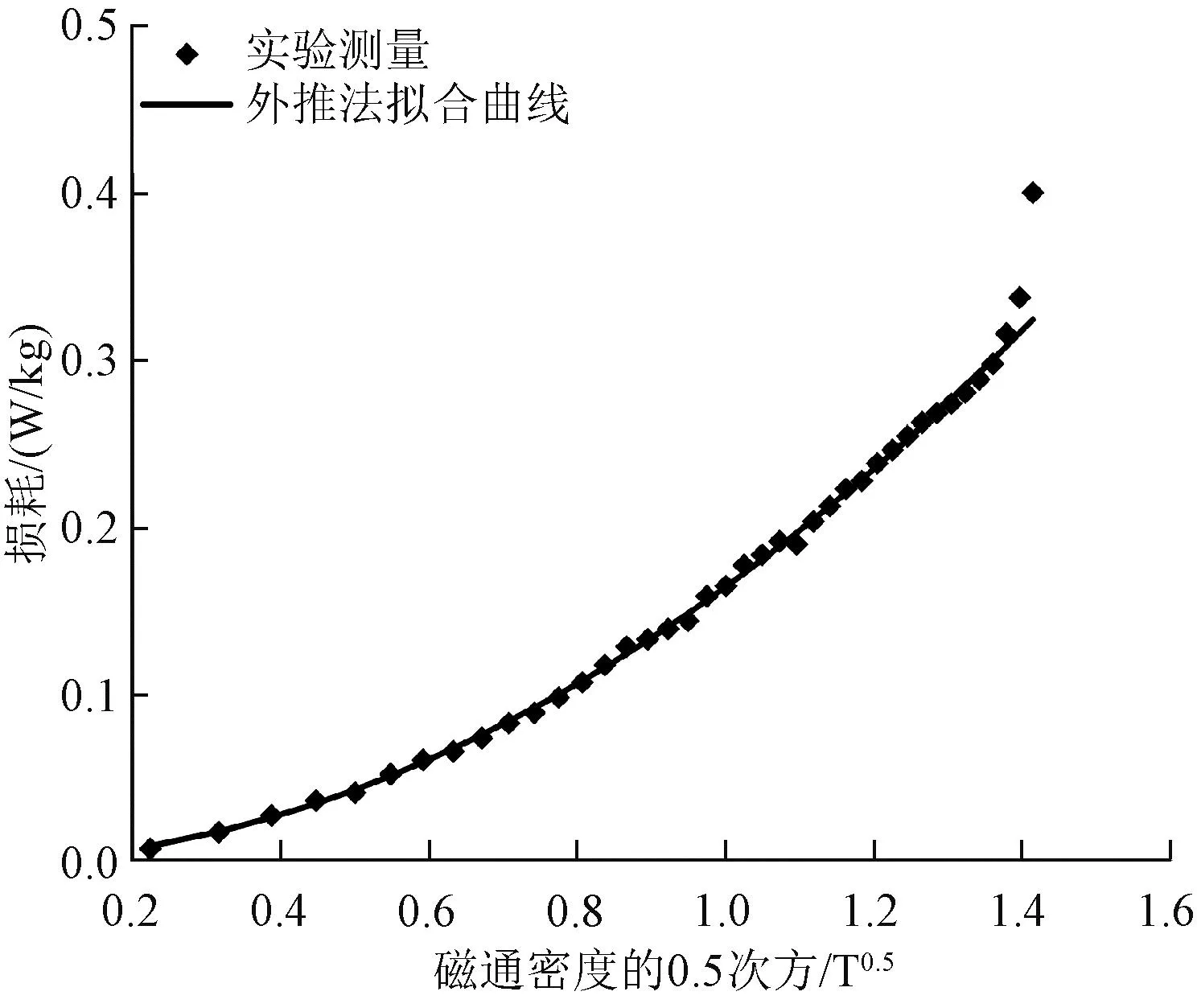
图8 损耗测量与曲线拟合图Fig.8 Loss measurement and curve fitting diagram

为了准确拟合磁滞损耗Phys,采用磁通密度峰值的多项式[34]替代式(5)中的常数m:

(19)

式中,a、b、c均为待求参量。利用工频下的测量数据[33]拟合式(19)中的各待求参量,拟合曲线的决定系数为0.995 7,拟合关系良好;拟合曲线与实验测量值的对比结果如图9所示。拟合后的损耗分离公式为:

(20)

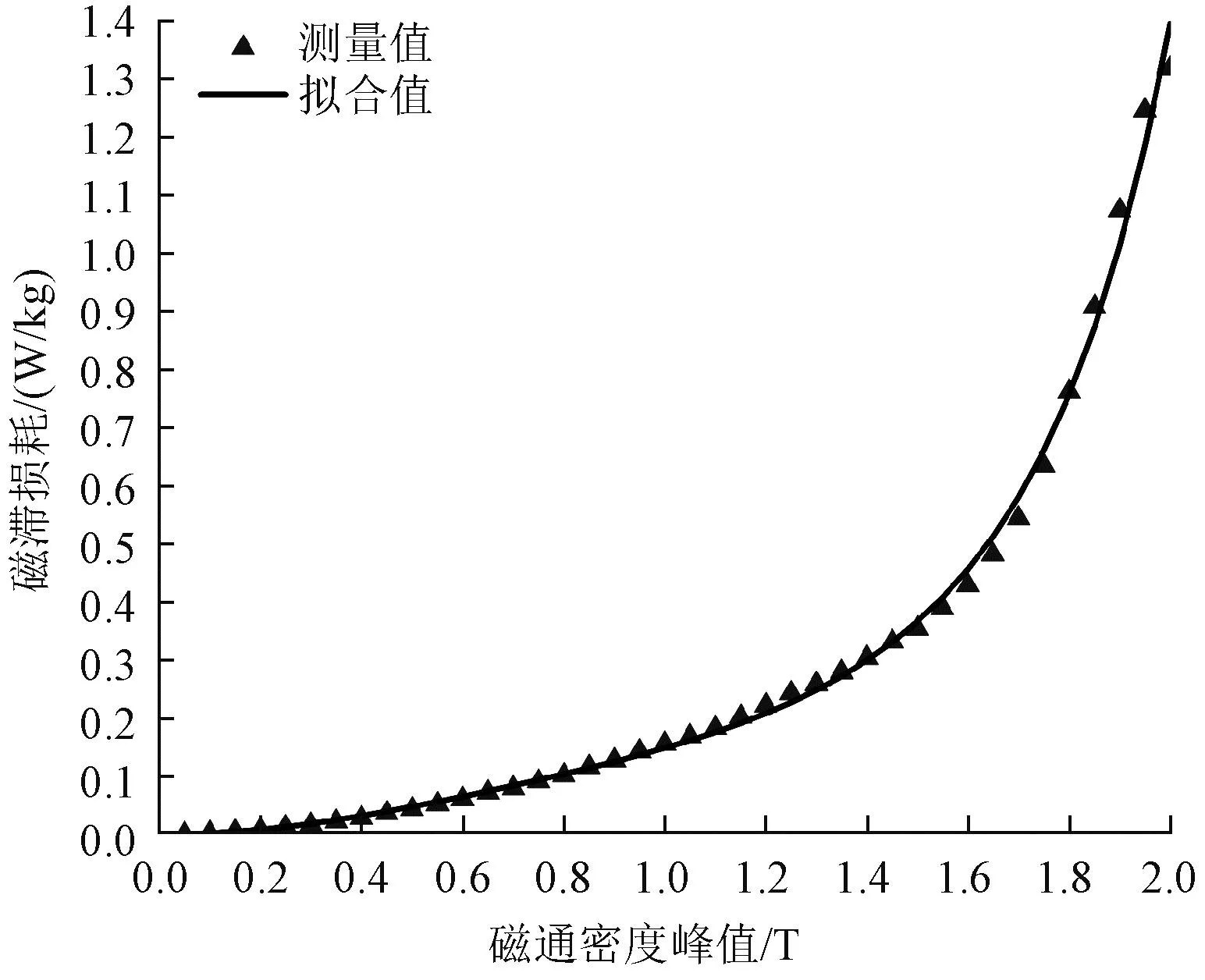
图9 磁滞损耗随磁通密度峰值变化图Fig.9 Variation of hysteresis loss with magnetic density peak

将式(20)代入式(17)即可求出硅钢叠片的磁滞损耗、涡流损耗以及剩余损耗。

4.2 计算结果与分析

4.2.1 磁通计算结果

计算激励电流为10 A时改进均质化与传统均质化的叠片磁通,结果如图10所示。对比反向激励、同向激励和单激励条件下10 A、15 A和25 A时未均质化、传统均质化与改进均质化的磁通计算结果,具体见表1。当迭代步数相同时,未均质化、传统均质化和改进均质化的平均误差绝对值分别为3.99%、3.19%和3.18%,表明改进均质化、传统均质化和未均质化有着同样的求解准确度。

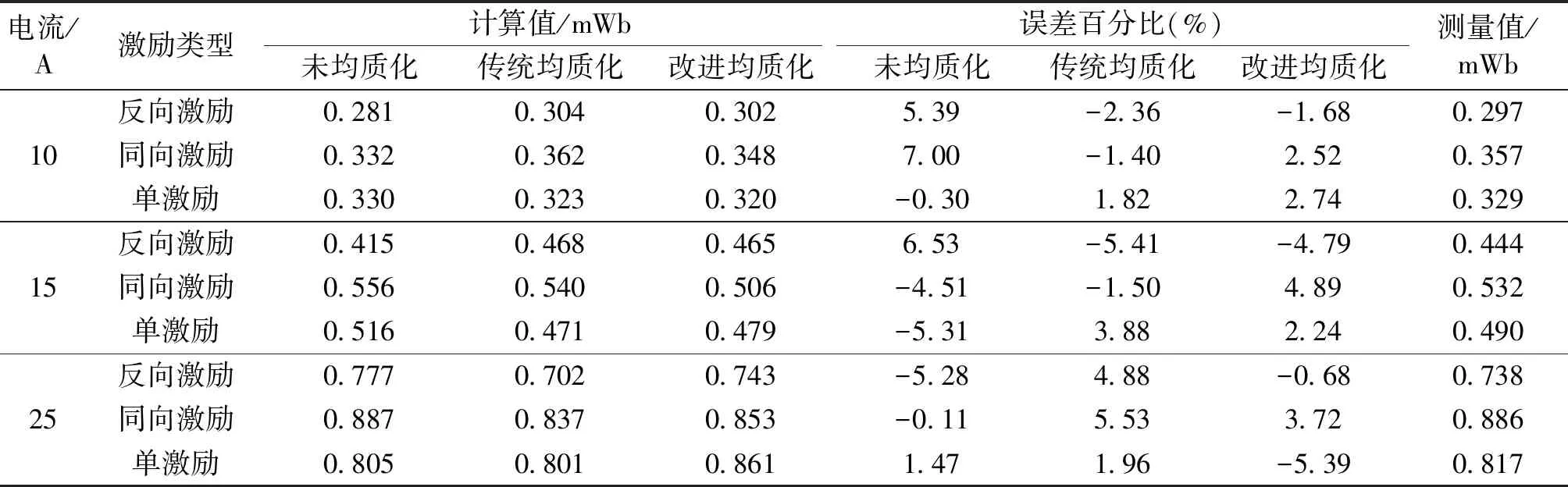
表1 硅钢叠片磁通计算结果Tab.1 Magnetic flux calculation results of silicon steel laminates

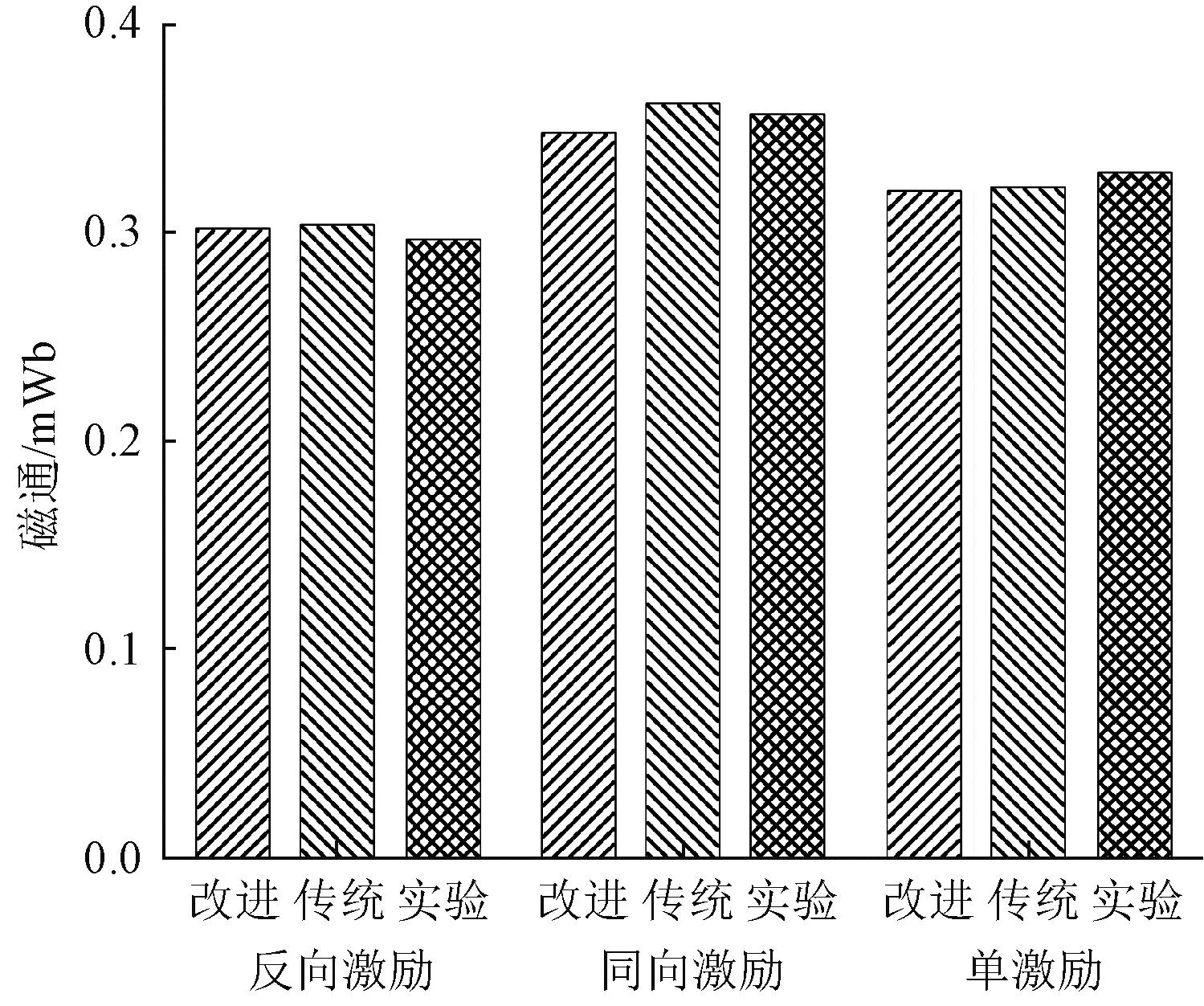
图10 磁通计算结果对比Fig.10 Comparison of flux calculation results

4.2.2 损耗计算结果

计算反向激励下10 A、15 A和25 A的总损耗、磁滞损耗、涡流损耗以及剩余损耗,结果见表2。由表2可知,激励电流10 A时虽然误差略大,但是仍然在工程允许范围之内;当激励电流为15 A和25 A时,计算结果与测量值相吻合,证明了式(20)对于损耗计算的准确性以及改进均质化方法对于磁通计算的准确性。

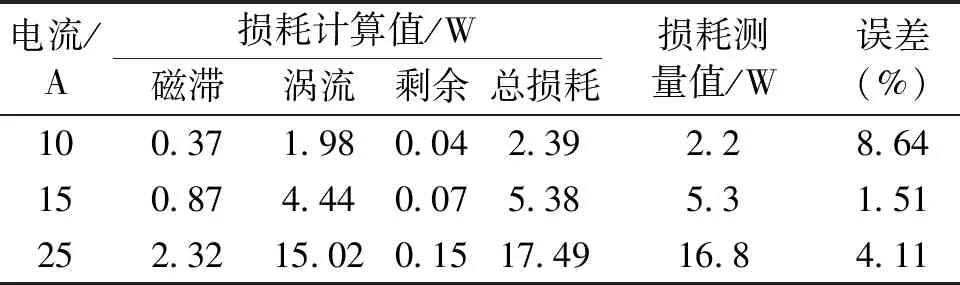
表2 硅钢叠片损耗分离计算结果Tab.2 Calculation results of silicon steel lamination loss separation

4.2.3 计算代价对比

利用处理器型号为i9-12900KF、内存为128 GB的计算机对比未均质化、传统均质化以及改进均质化在10 A反向激励仿真时的剖分单元数、内存消耗以及计算时间,结果如图11所示。当迭代步数相同时,未均质化的计算时间最长、剖分单元数最多、计算成本最高;传统均质化在计算时间上相较于未均质化时缩短了73.5%、内存消耗上减少了77.2%。进一步对比10 A反向激励、同向激励以及单激励条件下传统均质化与改进均质化的计算成本,对比结果见表3。由表3可见,相较于传统均质化,改进均质化使得有限元网格剖分平均缩减了43.0%、计算时间平均缩减了77.4%、内存消耗平均缩减了64.8%,表明改进均质化在传统均质化的基础上计算成本又有大幅减少,其原因是计算时间与内存消耗均与有限元的矩阵方程求解相关,减少剖分单元将直接减少矩阵方程维数,改进均质化在传统均质化的基础上进一步降低了叠片边缘处的剖分单元个数,从而减少了计算时间与内存消耗。结合磁通和涡流损耗的计算结果,证明了改进均质化不仅计算准确,计算代价也是最小的。

表3 10 A三种激励条件下计算代价对比Tab.3 Comparison of calculated costs under three different excitation conditions in 10 A

图11 归一化计算代价对比Fig.11 Comparison of normalized calculated costs

4.2.4 涡流分布对比

证明了改进均质化计算的准确性和高效性后,绘制激励电流为15 A时靠近线圈侧、远离线圈侧的涡流分布情况以及二维磁通分布情况,如图12～图14所示。发现同向激励时靠近线圈侧与远离线圈侧硅钢叠片铁心的涡流分布近乎一致;反向激励和单激励下叠片铁心靠近线圈侧和原理线圈侧的涡流分布差异较为明显;反向激励和单激励均在靠近线圈侧的硅钢叠片铁心的中心处存在一个主要的涡流回路。分析三种激励条件下的二维磁通分布图发现,反向激励下靠近线圈侧的磁通主要分布于叠片中心,而远离线圈侧的磁通则对称分布于左右两端,故其远离线圈侧的叠片铁心涡流分布出现了两个中心;单激励条件下由于激励的不对称,靠近线圈侧的磁通主要分布于有源线圈的两侧,故存在两个较为明显的涡流回路。同理,远离线圈侧的磁通主要分布于靠近有源线圈的一端,故存在一个较为明显的涡流回路。

图12 15 A反向激励涡流及磁通分布对比图Fig.12 Comparison of eddy current and flux distribution under 15 A reverse excitation

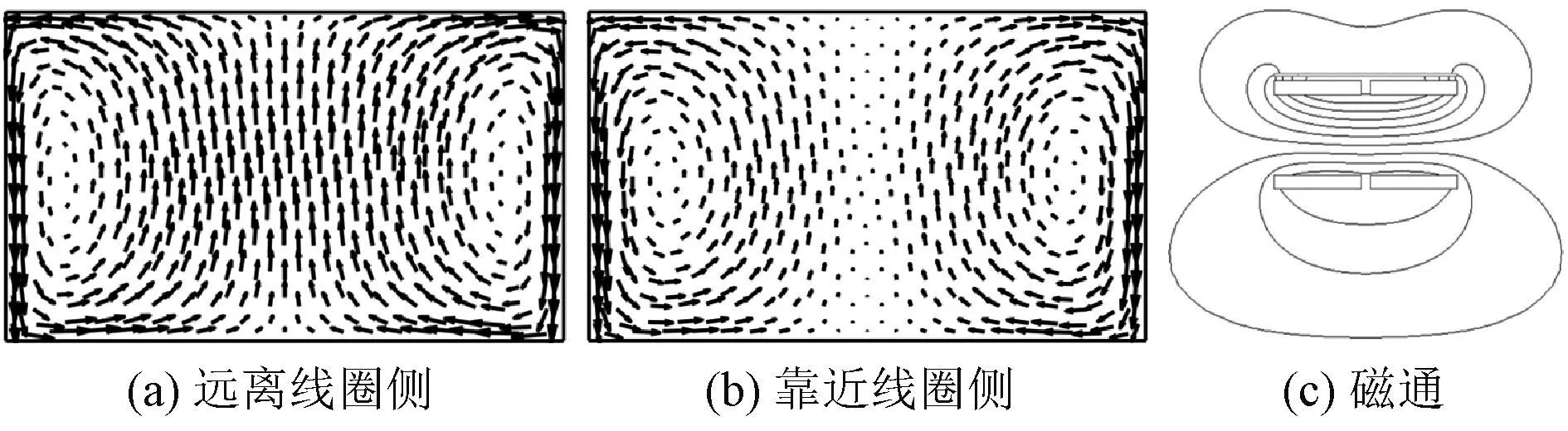
图13 15 A同向激励涡流及磁通分布对比图Fig.13 Comparison of eddy current and flux distribution under 15 A simultaneous excitation

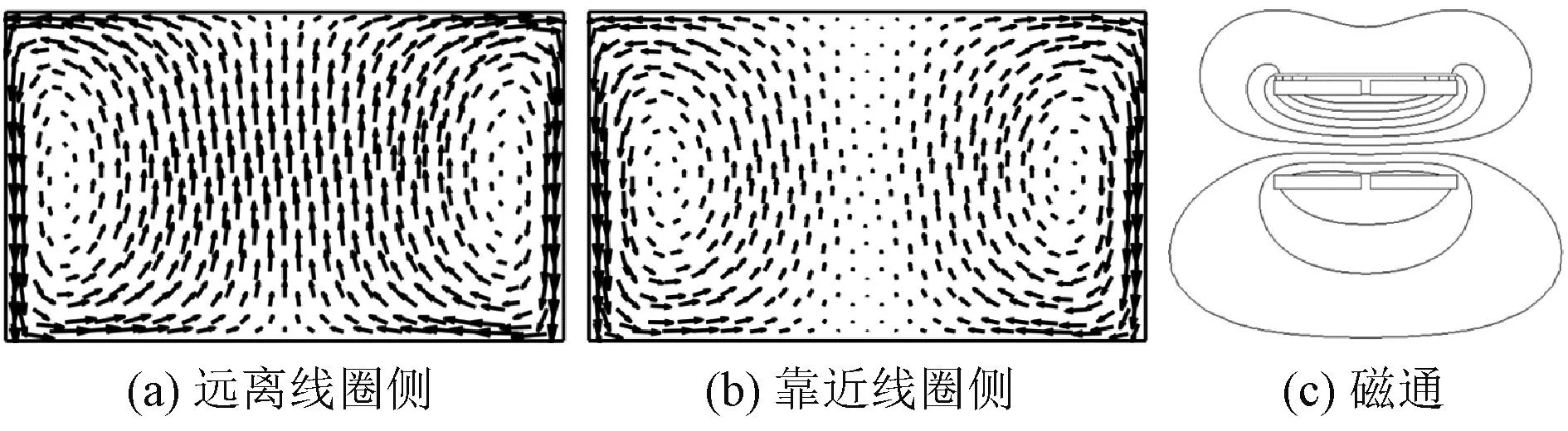
图14 15 A单激励涡流及磁通分布对比图Fig.14 Comparison of eddy current and flux distribution under 15 A single excitation

5 结论

(1)本文指出传统均质化在计算上因考虑集肤效应而额外进行网格剖分,计算成本相较未均质化有所减少,但仍然较高。通过引入等效复磁导率幅值,建立了考虑集肤效应的均质化公式。

(2)本文基于改进的均质化公式对TEAM P21d-M问题进行仿真分析,首先对比了未均质化、传统均质化和改进均质化在磁通计算上的差异,结果表明改进均质化与未均质化和传统均质化相比,计算准确度并没有显著劣化;改进均质化的计算误差绝对值不超过5%,最小误差绝对值仅为0.68%,进一步证明了改进均质化的计算准确性。

(3)在证明了改进均质化计算的准确性之后,对比了未均质化、传统均质化以及改进均质化之间在计算代价上的改变,仿真结果表明,迭代步数相同时,传统均质化相较于未均质化时计算时间上减少了73.54%,而改进均质化相较于传统均质化计算时间进一步减少了77.9%,在此基础上着重对比传统均质化与改进均质化的网格剖分数、内存消耗、计算时间。计算结果表明,相较于传统均质化,改进均质化在网格剖分数上平均减少了43.0%、内存消耗上平均减少了64.8%、计算时间上平均减少了77.5%,证明了改进均质化方法不仅计算准确,同时相比传统均质化方法有着更高的效率。

(4)后续工作中,将研究包括软磁复合材料、片间短路等情况下的均质化公式的改进。