基于GRNN-MC的变压器振动信号预测
2024-03-25钱国超张家顺代维菊朱龙昌王丰华
钱国超, 王 山, 张家顺, 代维菊, 朱龙昌, 王丰华
(1. 云南电网公司电力科学研究院, 云南 昆明 650217;2. 云南电网有限责任公司怒江供电局, 云南 怒江 673100; 3. 上海交通大学电气工程系, 上海 200240)
1 引言
变压器是电力系统的重要纽带,被誉为电力系统的“心脏”,它具有电压和电流转换的关键功能,并负责电能的分配和传输,若其发生故障将严重威胁电网的平稳运行,造成庞大的社会经济损失,甚至对人员造成伤害。据统计[1,2],绕组变形或松动一直是变压器占比最高的故障,且故障率居高不下。同时,电网中老旧变压器数量的增长给电网的安全稳定运行带来了较多的不确定因素。因此,主动推进变压器的状态监测工作,确保及时发现潜在的故障问题,对提升变压器运维的精细化水平、助推碳达峰碳中和意义重大。
振动信号是运行中的变压器极易获取的信号之一,与其绕组与铁心的机械状态密切相关,相关学者也已经意识到振动信号在变压器运行状态监测中的重要性,并从多个角度,例如变压器振动特性的理论计算[3-5]、变压器振动信号的特征提取[6-11]、基于数据驱动的变压器振动分析模型的构建及应用[11-16]等诸多方面进行了相关若干研究。具体来说,为获取变压器绕组机械状态辨识时振动信号特征参数的评判依据及缺陷模拟的便利性,现有研究大都针对模型变压器进行。如文献[12-14]基于某10 kV油浸式变压器空载试验、短路试验及负载试验下的箱壁振动信号分析结果,指出可依据变压器振动信号的基频分量判别绕组的运行状态,并建立了基于变压器电压、电流与振动信号基频分量之间映射关系的变压器振动计算模型。文献[15]中研究者选取了一台10 kV单相变压器进行实验,着重研究了在不同电流作用下绕组振动的传递规律,并提出了功率传播比的概念,为变压器振动监测时振动传感器放置位置的选取提供了重要的参考依据。文献[16]提出了一种新的变压器振动基频幅值计算方法,利用广义回归神经网络(Generalized Regression Neural Network, GRNN)来综合处理变压器运行电压、负载电流、油温和油箱表面振动信号。作为一种热门的机器学习方法,GRNN尤其擅长于模拟和解决非线性问题,能够凭借其网络优秀的函数逼近能力,对其输入输出之间的复杂函数关系进行映射[17],且具有训练速度快、处理效率高等优点。但在实际应用中发现,GRNN的预测结果会在一定范围内随机波动,预测效果不够稳定。
作为一种“无记忆性”的随机过程,马尔科夫链(Markov Chain, MC)能够通过研究事物的状态及状态转移,对事物未来发展趋势进行预测,适合描述随机波动问题[18]。为满足变压器运行状态快速判别的实际需求,助力构建新型电力系统,本文基于运行中的变压器振动信号,尝试采用GRNN和MC的联合方法,以研究变压器振动信号的变化规律,同时依据变压器负载电流来改进MC固有的初值敏感问题,用以提高预测精度。最后以运行中某500 kV变压器振动信号为例进行分析,以确定本文分析方法的有效性和准确性。
2 基于GRNN-MC的变压器振动信号预测模型
运行中的变压器箱壁振动信号为绕组振动和铁心振动的非线性叠加,与变压器的工作电压、负载电流等多种因素密切相关,且还受到传递特性尚不明确的变压器结构件和绝缘油等传递路径、箱壁结构的影响,映射关系较为复杂。而GRNN是一种基于数理统计的神经网络,可通过同时进行全局逼近和局部逼近来实现最佳函数逼近,在处理复杂问题时具备着强有效的非线性映射能力,其出色的鲁棒性使其能够适应不同的数据变化和挑战,保持准确性和可靠性,且训练速度快,处理效率高,适用于运行中的变压器海量振动监测信号的分析及其运行状态的高效准确判别。
2.1 广义自回归神经网络
图1为GRNN的基本结构示意图,它由输入层、模式层、加和层和输出层构成,每个部分承担着不同的功能。图1中,X=(x1,x2,…,xm)T和Y=(y1,y2,…,yk)T分别为网络输入和输出;m和k分别为网络输入和输出维数。由于输入层中包含m个输入神经元,其数量与输入维数相匹配,因此可将输入数据经过线性单元传递至模式层。GRNN的模式层包含n个神经元,这个数量与训练样本的个数相等,每个神经元与一个训练样本相关联,其传递函数可表示为[17]:
(1)
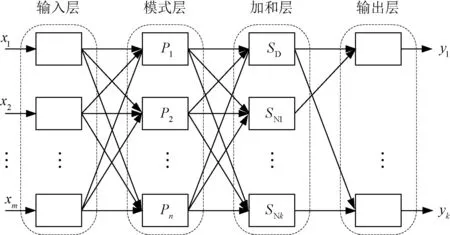
图1 广义回归神经网络基本结构Fig.1 Basic structure of GRNN
式中,Pi为模式层的输出值;Xi为输入层中的训练样本,均与第i个神经元相对应;σ为散布参数。
式(1)中,σ决定着模式层与加和层中神经元的连接权重,其取值为(0,1)。具体来说,当σ趋向于1时,网络倾向于从全局样本对输入进行逼近;当σ趋向于0时,网络则重点考虑与输入距离最近的样本。
在加和层中包含两类神经元,分母单元负责对模式层内各神经元的输出进行求和,而分子单元则是用于求解其加权和,对应的传递函数分别为[17]:
(2)
(3)
式中,αij为第i个神经元与加和层中第j个神经元之间的连接权重值。
输出层的神经元数量与输出样本数量一致,将加和层中各分子单元除以分母单元即可得到输出层的神经元函数,为:
(4)
显然,只要GRNN的输入和输出被确定,对应的网络结构也就随之被完全确定,这也是GRNN训练速度快、处理效率高的根源所在。
2.2 样本数据集构建和网络训练
绕组振动和铁心振动是产生变压器振动信号的主要原因,而这些振动与负载电流和运行电压之间有着密切的联系,故本文将变压器负载电流和运行电压作为GRNN的输入训练样本,记作X。根据现有研究易知[6-8],运行中的变压器箱壁振动信号多为100 Hz分量及其倍频分量,且这些频谱分量与变压器绕组及铁心的工作状态的相关性存在明显不同,故本文采用层次分析法(Analytic Hierarchy Process, AHP)计算变压器振动信号各个频谱分量的权重,据此计算归一化特征频率作为GRNN的输出Y及变压器运行状态的评判依据。此处,振动信号归一化特征频率的计算公式为:
(5)
式中,b为振动信号频谱分量的个数;fi、vi和wi分别为第i个频谱分量及其幅值、权重。
AHP算法主要用以计算复杂系统决策过程中的考虑因素的权重,其特点在于,在计算过程中,通过定性判断因素之间的相对重要性,建立判断矩阵,最终计算出定量的权重矢量[19]。具体应用时,需要以两两对比的方式来导出元素间相对重要性的比例关系,以此建立起具有统一标度的判断矩阵作为测度依据。对变压器箱壁振动信号来说,可结合现有研究从变压器绕组及铁心振动频谱分量与其典型故障的紧密程度考虑,据此构建完全判断矩阵。
确定了GRNN的输入和输出之后,其训练过程的本质即为确定散布参数σ的过程。本文在此采用K折交叉验证法,即首先将全部训练样本随机分为K个大小相同的训练样本子集,然后依次选取其中1个样本子集作为验证集,其余K-1个样本子集作为本次的网络训练样本进行1次网络训练,重复这一过程直至总计训练达到K次。在该过程中,设置散布常数σ在区间(0,1)内以设定步长递增。同时,为确定散布参数σ最优取值,选取验证集中的实际值与网络预测值的均方差(Mean Squared Error, MSE)来衡量网络训练模型的性能,即在K次交叉验证训练完成后,从验证集中选取实际值与网络预测值的MSE最小值所对应的σ作为最优散布参数。此处,MSE的计算公式为:
(6)
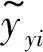
2.3 马尔科夫链
马尔科夫链是一种特殊的随机过程,其基本原理为:对于某个离散时间序列系统,该系统的所有状态可用随机变量表示,每个状态对应一定的概率,称为状态概率;系统由当前时刻状态转移到下一时刻状态的过程中存在着概率转移,称为转移概率。依据状态概率和转移概率可以根据当前时刻的状态推断下一时刻的状态概率分布,进而预测出下一时刻的系统状态[20]。
MC主要由状态划分、概率转移矩阵以及误差修正三部分组成,分别为:
(1)状态划分
设GRNN计算得到的变压器振动信号与实测振动信号归一化特征频率的相对误差序列为:
E={ε1,ε2,…,εn}
(7)

(2)构建状态转移概率矩阵

(8)
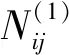
据此可构建一步状态转移概率矩阵为:
(9)
(3)误差修正
A(k)=A(0)Pk=A(0)P1P2…Pk
(10)
由A(k)可计算出变压器振动信号落入各个状态区间的期望,据此,便可以修正k时刻的GRNN计算结果为:
(11)
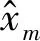
综上,可得出基于GRNN-MC的变压器振动信号预测模型的具体实现流程如图2所示。
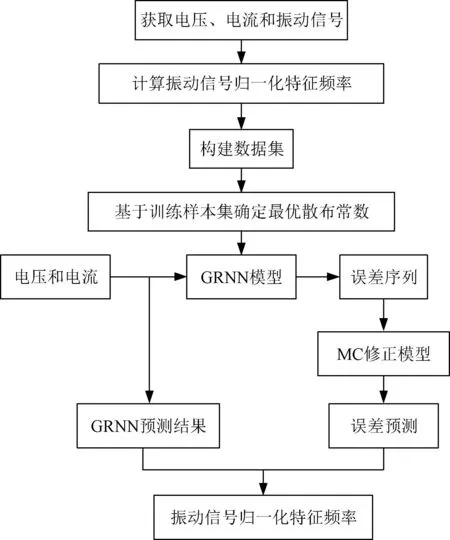
图2 GRNN-MC变压器振动预测模型实现流程Fig.2 Flow chart of vibration prediction model of transformer by GRNN-MC
3 结果分析
以某500 kV变压器的振动在线监测数据为案例,着重对电压、电流和箱壁振动信号进行监测分析,其中,电压和电流信号的采样频率为2.56 kHz,振动加速度传感器放置于变压器低压侧中间偏下距离箱体下沿约1/4箱壁高度处,且注意避开加强筋,其采样频率为10 kHz。
图3为500 kV主变振动信号的频谱分布及其负载电流与振动基频比重的变化曲线。此处,振动基频比重指变压器振动信号100 Hz分量在其频谱总能量中的比重。由图3可见,变压器的振动信号主频为100 Hz,其各倍频为次要分量,均随负载电流的变化而改变。此外,振动信号基频占比随负载电流变化呈现出一定的相关性,其主要原因在于:变压器100 Hz振动信号主要由铁心和绕组振动引起,其分别与变压器的工作电压和负载电流密切相关,而前者基本上保持恒定,故当变压器的负载电流变化时,其振动信号的振动基频比重亦随之波动。
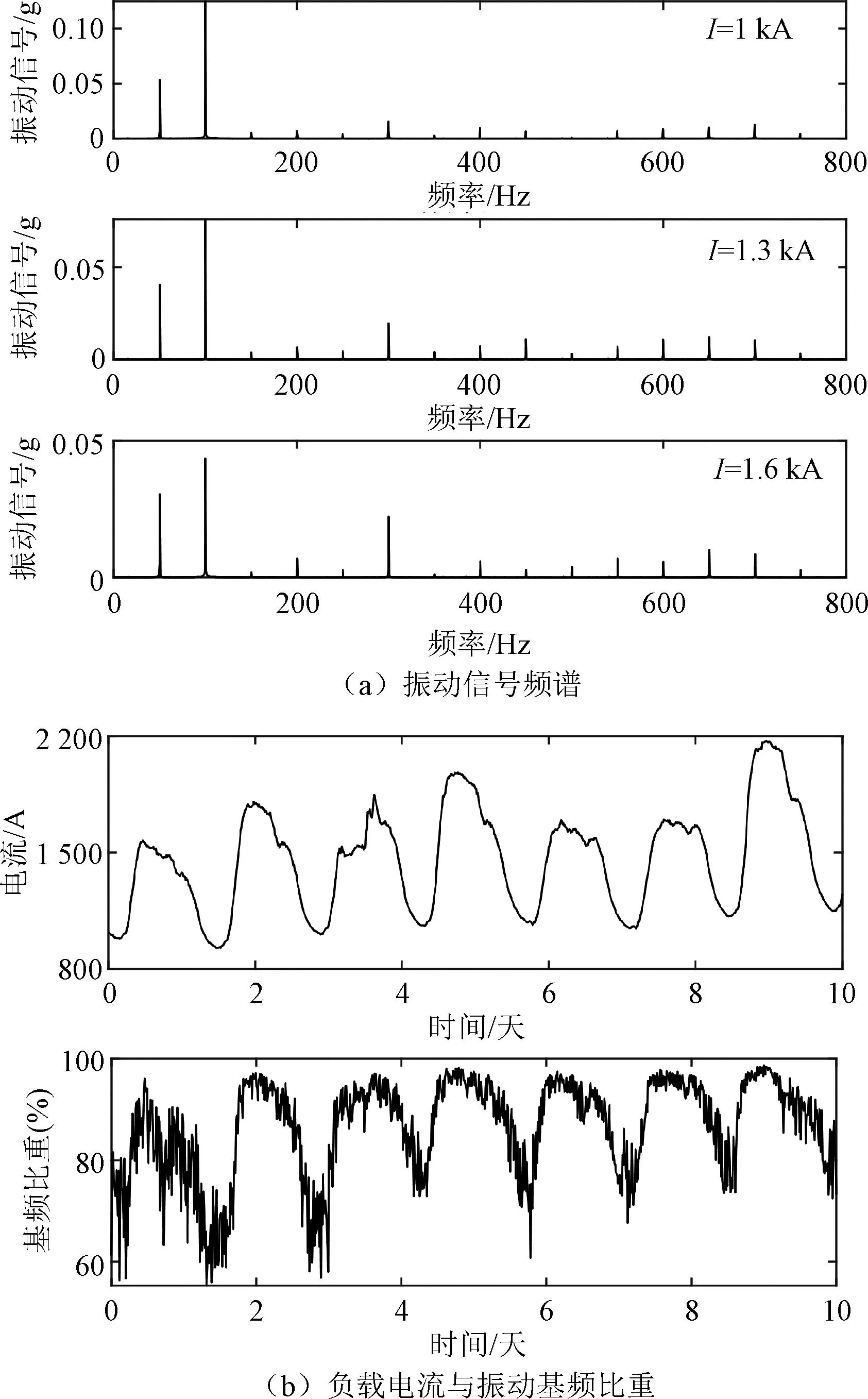
图3 变压器的载电流与振动信号频谱Fig.3 Frequency spectrum of vibration signals and load current of power transformer
根据变压器振动信号在800 Hz内的频谱分布,采用AHP及式(5)计算其频谱分量的权重。具体来说,需要依据振动信号各个频谱分量和绕组及铁心故障的相关性,综合分析本文所获取的振动信号,可认为200 Hz、300 Hz与绕组松动或变形等缺陷的相关性更高,400 Hz及以上的频谱分量与铁心故障的相关性更高。据此可通过构造判别矩阵并进行一致性分析,可得变压器箱壁振动信号的频率分量权重见表1。

表1 振动信号频谱分量权重Tab.1 Weight of different components of frequency spectrum for vibration signals
进一步地,使用其中1个月的监测数据构建GRNN数据集,将其分为三组,第一组样本为2017年4月1日~4月24日的监测数据,用于构建GRNN模型;第二组样本为2017年4月25日~4月29日的在线监测数据,用于构建MC修正模型;第三组样本为4月30日的在线监测数据,用于对变压器振动信号预测模型的计算结果进行验证。
使用5折交叉验证法对所建立的第一组样本进行训练,对应的交叉验证结果如图4所示。由图4可知,当散布参数取0.15时,平均均方差最小值为0.018,此时神经网络的预测效果达到最优,故本文设定σ=0.15。

图4 5折交叉验证结果Fig.4 Result of 5-fold cross validation
应用训练完成的GRNN模型对第二组样本中的振动信号进行预测,计算结果如图5所示。由图5可知,GRNN对变压器振动信号的总体预测效果良好,与实际结果基本吻合。但是,在部分时刻上,振动信号的预测结果和实际结果之间仍存在较大的偏差。
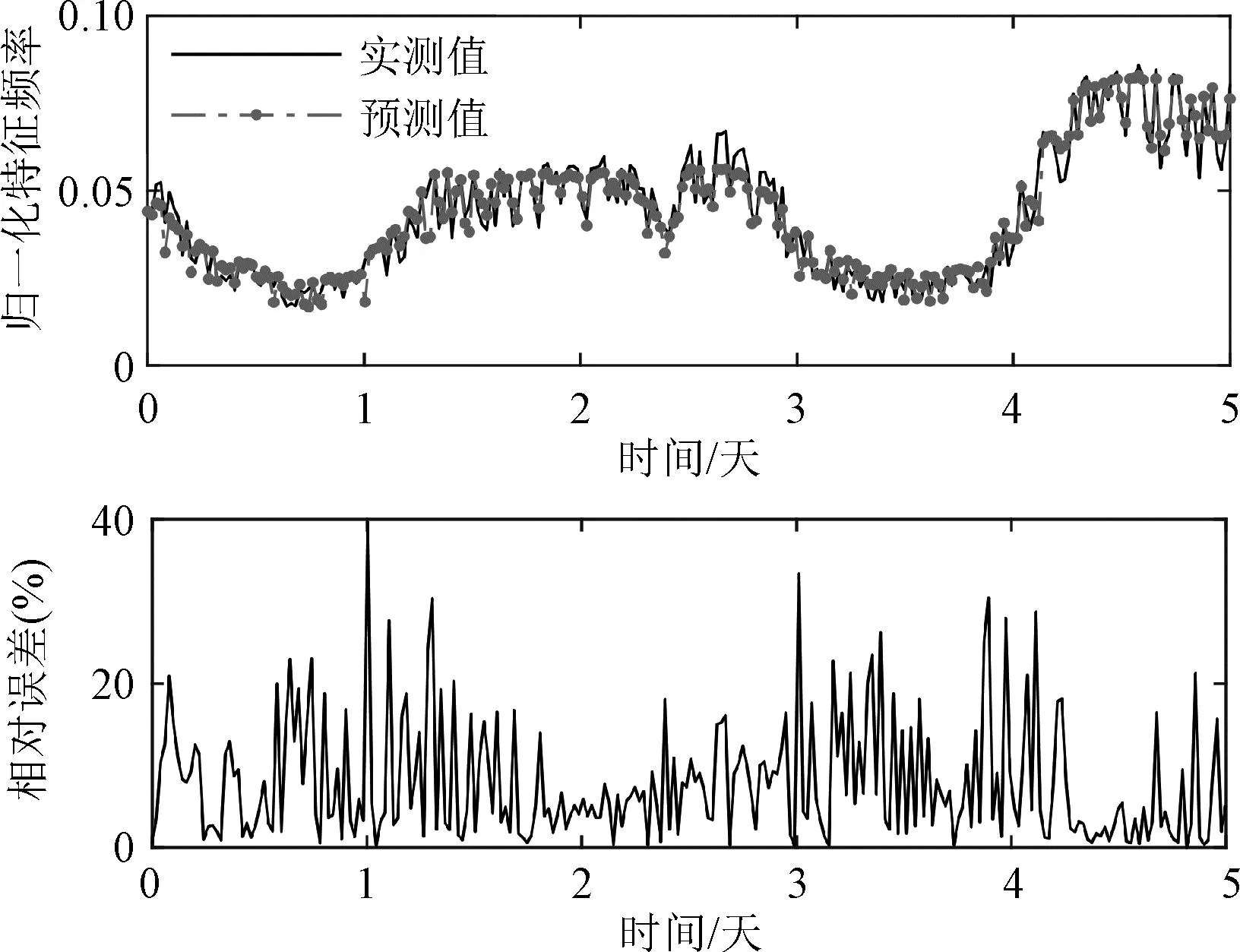
图5 广义回归神经网络预测结果Fig.5 Prediction results of GRNN
计算GRNN模型的振动信号预测结果与实际结果的相对误差,并将其划分为5种状态,分别为:z1(-0.101 2,-0.032 8);z2(-0.032 8,-0.009 3);z3(-0.093,0.037);z4(0.037,0.061 3);z5(0.061 3,0.184 7)。接着,依据相对误差序列,计算得到一步转移概率矩阵为:
P1=
最后,计算得到第二组样本中最后时刻的相对误差为-0.032 7,属于状态3。依据一步转移概率矩阵,确定系统的初始概率向量,在此基础上便可对下一时刻的相对误差进行滚动预测,并修正广义回归神经网络的预测结果。
使用本文所提方法对第三组样本中的变压器振动信号进行预测,所得预测结果及预测结果相对误差的评价指标分别如表2和图6所示。同时,为体现本文所提方法的优越性,给出了仅使用GRNN的振动信号预测结果。由表2和图6可见,与单纯使用GRNN得到的振动信号预测结果相比,经MC修正后的GRNN预测结果相对误差的最大值、均值及均方根值都得到了提升,预测误差更小、可信程度更高。说明了使用MC对变压器振动信号预测结果修正的有效性,同时也验证了本文所提方法应用于变压器绕组状态振动预测的准确性和可靠性。
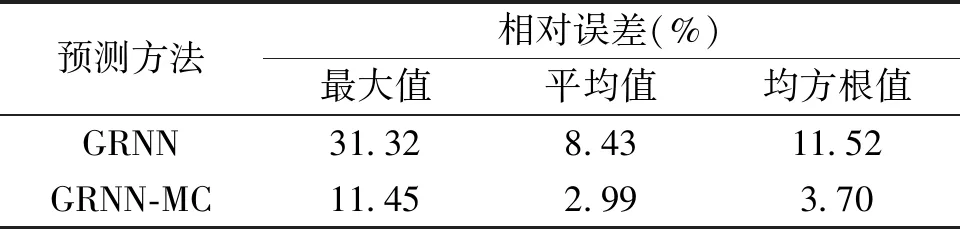
表2 使用GRNN-MC与GRNN的振动信号预测相对误差评价指标Tab.2 Error evaluation criteria of relative error of vibration signals by GRNN and GRNN-MC
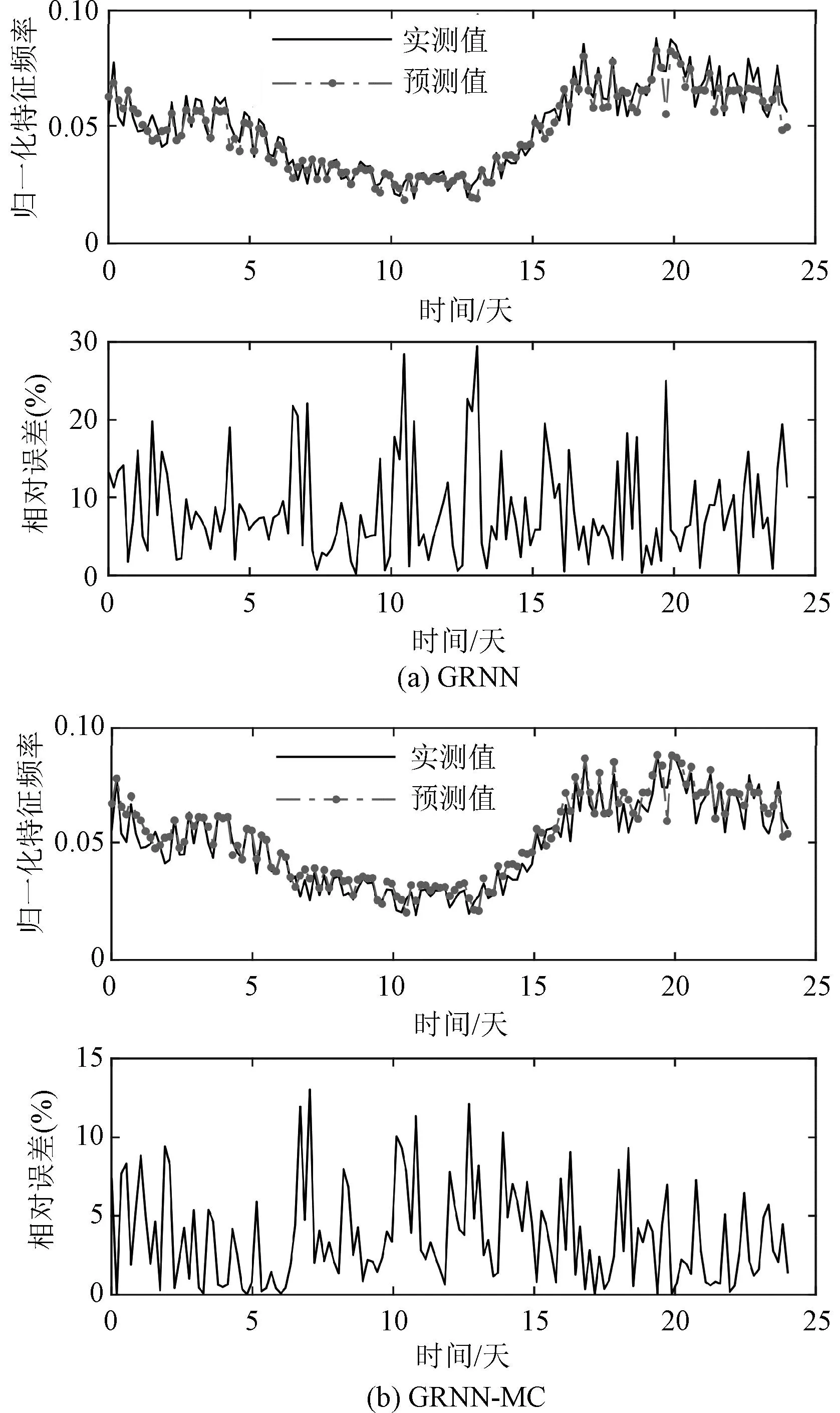
图6 使用GRNN-MC与GRNN的振动信号预测结果Fig.6 Prediction results of vibration signals by GRNN and GRNN-MC
在实际应用中,可通过对比本文所提方法获得的振动信号预测结果和实测振动信号的归一化特征频率,若二者的偏差超过设定的阈值且呈现增大趋势,则需要关注变压器绕组的运行状态,必要时,辅以其他判别方法进一步判定绕组状态,有效避免变压器故障的发生。
4 结论
(1)本文所提基于广义回归神经网络和马尔科夫链的变压器振动信号预测方法,通过变压器的运行电压和负载电流,高效且准确地预测了振动信号的归一化特征频谱。
(2)本文所定义的变压器振动信号归一化特征频率充分考虑了与变压器绕组及铁心状态密切相关的振动信号频率分量及其权重,在实际应用中,可通过对比本文所提方法获得的振动信号预测结果和实测结果,实时评估运行中变压器的机械状态,掌握变压器机械状态的发展动向,实现变压器机械状态的预警分析。
(3)本文所提方法具有一定的普适性,应用于不同型号的变压器时,只需基于变压器历史监测数据构建广义回归神经网络模型和马尔科夫链修正模型,即可进行变压器振动信号的预测分析,这也是下一步工作的重点。
