串珠状溶洞数量影响灌注桩顶部水平受拉特性试验研究

周德泉 ，海军 ，刘宏利 †，高祁 ，刘海龙 ，桂海麒 ，孙卫勇 ，谢瑞庭 ，朱沁 ，周毅

（1.长沙理工大学 土木工程学院，湖南 长沙 410076；2.中交四航局第六工程有限公司，广东 珠海 519000；3.中国路桥工程有限责任公司，北京 100011）

随着国家基础设施建设的发展，电塔基础、钻井平台和桥梁等工程常将桩基础嵌入岩体，以抵抗强大的倾斜、垂直或者水平荷载，因此嵌岩桩的水平承载特性成为桩基础工程的研究新热点之一.

理论研究方面，Carter 等［1］基于岩土体介质的小孔扩张理论分析嵌岩桩水平承载性能，给出了嵌岩桩水平位移和内力的弹性解析结果.Li 等［2］认为嵌岩桩桩周岩体阻力按余弦函数变化，并引入桩侧阻力修正系数，推导了嵌岩深度理论计算公式.张坤勇等［3］基于多组嵌岩桩水平受荷现场试验数据，以双曲线函数为判别准则，对Kulhawy 计算模型进行修正.

数值模拟方面，王永艺等［4］、牟冬辉等［5］、刘润等［6］采用有限元方法分析了嵌岩深度、桩径、露头高度等对桩顶水平加载下嵌岩桩承载特性的影响，认为嵌岩深度和桩径与水平承载力呈正相关，与露头高度呈负相关.张浦阳等［7］通过数值模拟分析嵌岩桩的水平承载性能，认为最佳嵌岩深度为2 倍桩径，桩身弯矩最大值位于岩土交界处，横截面水平剪力方向在岩土交界处发生改变，嵌岩段桩身剪力方向与加载方向相反.张坤勇等［8］采用有限元方法模拟了嵌岩桩水平加载试验全过程，认为嵌岩桩桩侧岩体的破坏不是由岩石本身强度参数控制，而是岩体中的节理、裂缝及软弱夹层等结构面控制.贺国京等［9］利用现场资料结合有限元分析探讨了溶洞半径、顶板厚度及基桩弹性模量对嵌岩桩水平承载力的影响，认为溶洞半径增大，顶板厚度减小，桩顶水平位移增加，基桩承载力减小，而基桩弹性模量增大，桩顶水平位移减小，但最大拉应力增大.

试验研究方面，管金萍等［10］对嵌岩桩进行了桩顶无约束单向循环水平静载试验，发现地基水平抗力系数随着水平力和水平位移的增大逐渐减小.张埕豪等［11］通过室内模型试验分析了岩层倾角对嵌岩桩水平承载特性的影响，认为岩层倾角越大，嵌岩桩承载力越小，其中岩层逆向倾斜相比顺向倾斜对桩基承载更加不利.王多垠等［12］通过室内模型试验研究全嵌岩桩的变形与稳定问题，发现弯矩峰值点大约出现在岩面下入岩深度的90%处.劳伟康等［13］、王建华等［14］结合实际工程，采用大直径嵌岩桩水平承载试验，分析了嵌岩桩的桩身应力、弯矩、水平位移等参数的变化规律，认为岩土交界处会出现附加应力集中，建议加强此处桩身配筋.Fan［15］、刘孟瀚等［16］、杨鹏帅等［17］结合室内试验与数值模拟，研究桩端下部、桩侧溶洞对嵌岩桩水平承载特性的影响，认为桩侧和底部都有溶洞对桩基水平承载力影响最大，底部溶洞次之，桩侧溶洞影响最小.李天雨等［18］通过模型试验，分析、探讨了桩基嵌固在岩溶临空面附近时的承载力，认为临空面的存在降低了嵌固端的承载力，且桩前临空面对桩嵌固端承载力的影响更显著.此外，区别于被动桩［19］，赵明华等［20］对国内外相关领域文献及湖南大学历年来研究成果进行总结分析，重点介绍了陡坡段桥梁桩基的承载机理、试验方法、受力变形分析及其设计计算方法，以及施工技术、安全评价方法和加固处治措施，并给出了一些发展建议.

学者们从理论研究［1-3］、数值模拟［4-9］和试验研究［10-18］3方面开展嵌岩桩的水平承载特性研究.岩溶发育区的嵌岩桩可能刺穿多层溶洞.文献［9，15-18］研究了溶洞对嵌岩桩水平承载特性的影响，但主要考虑溶洞位于桩侧或者桩底，很少考虑溶洞被桩体刺穿的情况，刺穿多层溶洞嵌岩桩的水平受拉特性尚不清楚，制约了岩溶区桩基水平抗拉能力的应用与发挥.基于岩溶区桩体单侧堆载效应［21］，本文采用室内模型试验，对比测试桩体分别刺穿0 个、1 个、2 个、3 个溶洞，桩顶承受水平荷载时嵌岩桩的桩身水平位移、应变、土压力，分析桩身水平位移、弯矩、土压力、土抗力及p-y曲线变化规律，研究串珠状溶洞数量影响灌注桩顶部水平受拉特性，为岩溶区刺穿多层溶洞嵌岩桩的水平承载力设计与应用提供试验依据.

1 模型试验概况

本次室内模型试验所用的模型箱尺寸为1 420 mm×750 mm×1 100 mm（长×宽×高），采用砝码、滑轮和钢绞线施加水平荷载.试验前先用刚性隔板将模型箱分割成4 个大小相同的独立区，4 根试验桩依次放置在每个隔室中心，从左到右分别为未刺穿溶洞桩A0、刺穿1个溶洞桩A1、刺穿2个溶洞桩A2及刺穿3个溶洞桩A3.基岩坡面和上层覆土层坡面倾角为10°，土层厚度为300 mm.在桩顶分级施加水平荷载，通过对比测试，揭示刺穿0 层、1 层、2 层、3 层溶洞的基桩在水平荷载作用下桩身弯矩、水平位移和桩侧土抗力变化规律.试验整体布置如图1所示.

图1 试验整体布置图Fig.1 Overall test layout

1.1 模型相似常数的确定

影响本次模型试验的物理量有10 个：弹性模量E、重度γ、黏聚力c、内摩擦角φ、泊松比μ、水平荷载F、桩长L、线位移δ、应变ε和应力σ，依相似原理，写出模型试验相关参数表达式，如式（1）所示.选取水平力F和桩长L作为基本量，则式（1）中就只有8 个非独立变量，根据相似第二定理（π定理），则π函数的表达式如式（2）所示.

用C表示原型与模型之间的常数，若原型与模型之间是相似的，则原型与模型之间对应的线性长度及重度的比值为常数，经量纲分析，计算出各项π值，并假定几何相似常数和重度相似常数，根据π定理可导出其他物理量的相似常数，如表1所示.

表1 物理量的相似常数Tab.1 Similar constants of physical quantity

1.2 模型材料

实际工程中，桩以弹性变形为主，故模型试验中主要考虑其弹性模量.工程中灌注桩弹性模量Ep一般为30.00～32.50 GPa，由1.1 节相似常数可得模型桩弹性模量Ep为3.00～3.25 GPa，由一定级配的集料、水泥和水配合而成的混凝土桩最接近于模型桩弹性模量，但本次模型试验结构尺寸小，混凝土不容易制作成模型桩所需要的尺寸，故选取与其弹性模量较为接近的塑料模拟混凝土灌注桩.最终选择内边长为31 mm、外边长为40 mm、长度为1 000 mm 的PVC 管作为混凝土灌注桩的模型材料，通过简支梁法测得其弹性模量为3.30 GPa.为防止基岩模拟材料在振捣密实和凝结硬化放热过程中损坏应变片，模型桩应变片采用“内贴法”粘贴：将4 根PVC 管分别沿竖直轴线方向剖成两个半合管，在每根桩两个半合管内壁按设计间距对称粘贴应变片.为准确得到交界面处弯矩变化规律，土层与岩层交界面上下分别布置两组应变片，溶洞顶部、中部、底部各布置一组应变片，其他位置均匀布置［图2（a）］，将两个半合管用环氧树脂黏合，并在溶洞空腔范围内桩身4个侧面粘贴PVC 管片，来模拟冲击钻孔施工造成的溶洞内桩身“鼓肚”现象［图2（b）］.

图2 溶洞与模型桩Fig.2 Caves and model piles

现场岩土体分两种类型：上层黏土和下层中风化灰岩.在模型试验中，上层土体取自试验场地附近某土坡的红黏土，经过晾晒、粉碎、筛分，过5 mm 滤筛；下层中风化灰岩采用相似材料来模拟，其作为持力层，在模型试验中，模拟材料的弹性模量是主要考虑因素.试验采用细砂为集料，用石膏和水泥为胶结物，借鉴相似材料模拟研究成果［22-23］，筛选出适合本试验的模拟灰岩材料配合比为50∶7∶3（m砂∶m水泥∶m石膏）.

溶洞空腔采用木盒模拟.木盒采用厚度为11 mm的木板按溶洞大小设计和制作，长、宽和高分别为240 mm、200 mm 和100 mm，其中顶板和底板中心预留40 mm×40 mm 方形孔［图2（c）］.组合模型桩与溶洞，将模型桩穿过木盒并固定在设计位置［图2（d）］.

1.3 安装与测试

根据现有的水平受荷桩的试验成果［23］，当加载方向和垂直加载方向的箱内侧壁与模型桩之间的距离分别大于6倍桩径和4倍桩径，模型箱底面与模型桩底之间的距离大于3 倍桩径时，可以忽略模型箱的侧壁和底板对试验结果的影响.本文加载方向最小距离为6.25 倍模型桩边长，垂直加载方向距离为4.44 倍模型桩边长，底部距离为3.25 倍模型桩边长，均满足上述条件.为进一步减小边界效应的影响，浇筑基岩模拟混合料前，在每个隔板和模型箱内壁涂抹凡士林，覆盖聚乙烯薄膜.

试验前期准备过程中，对模型桩底部进行密封处理，为了保证模型桩垂直，当填筑混合料至桩底标高处后，在模型箱顶部利用10 根两两垂直的尼龙绳固定模型桩的顶端位置，并用刻度尺标记桩底的中心点位置，确定准确位置后，将模型桩放入模型箱中，继续浇筑混合料至设计位置并振捣密实，人工将顶面抹成倾斜面，标准养护28 d.养护期间在土层段桩身，从地表下20 mm 起每隔80 mm 粘贴一对土压力盒，并在桩身位移测点粘贴长30 mm、直径为18 mm 的塑料软管，在位移测点对应的木板上钻孔（ϕ20 mm），插入空心PVC 硬管，其一端套在桩身的软管上面，另一端留在木板外侧，百分表探针穿过孔道内至模型桩，其表座固定在独立的基准桩上，以测量加载过程中桩身的侧向位移.为保证填筑黏土的均匀性，试验采用了分层填筑的方式，将每一层填筑的黏土厚度统一控制为60 mm，填筑完成后将表面抹成与基岩层面相同的倾斜面，自重沉降两周，如图3所示.

图3 现场试验Fig.3 Test site

在模型箱上安装定滑轮，将钢丝绳的一端固定在模型桩的预加载孔中并反向绕过桩顶，另一端通过定滑轮固定砝码托盘，桩顶和定滑轮处于同一高度，确保了加载方向为水平.试验参照行业规程［25］，采用慢速维持荷载法，分8 级加载，第一级为50 N，此后每级增加50 N，通过TDS530 静态应变测试分析系统采集数据，第一级荷载施加前记录初始位移、应变和土压力数据，加载后每隔30 min 记录一次百分表读数，当两次读数差值小于0.01 mm 时，说明已达到稳定状态，记录此时百分表读数、应变和土压力数据，继续加下一级荷载，至最大荷载400 N 后停止加载.

2 试验结果与分析

2.1 桩顶水平位移

图4 为各桩桩顶水平位移-荷载曲线.由分析可知：

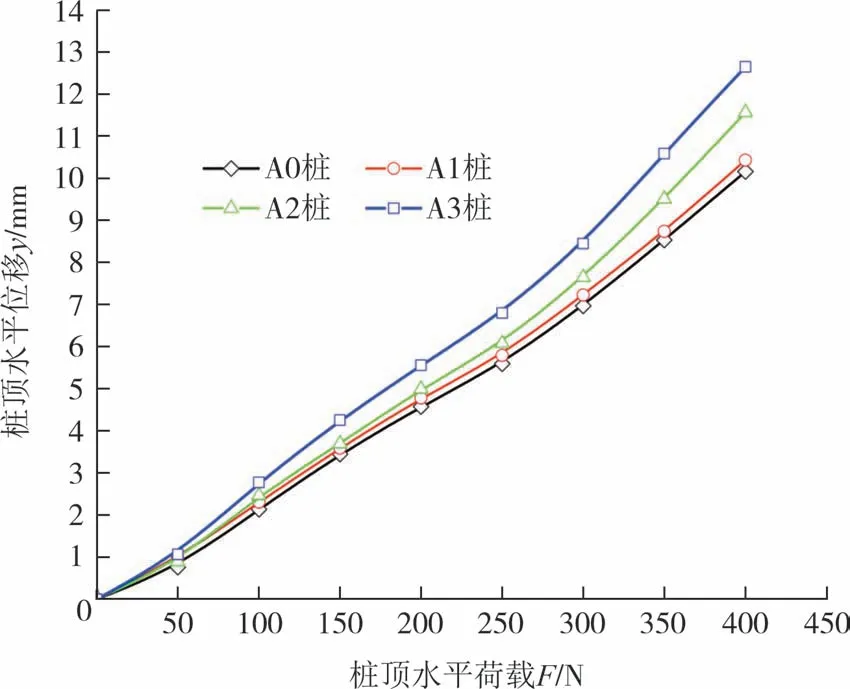
图4 桩顶水平位移对比Fig.4 Comparison of horizontal displacement of pile top

1）单桩顶部水平位移随水平荷载增大而增大.随着水平荷载的增大，基桩在地表处的水平位移具有类似的变化规律.在加载初期，抗力主要由靠近地面部分的土体提供，桩周土体处于弹性阶段，土体的变形也主要是弹性变形，桩顶水平位移随水平荷载增大而近似线性增大；随着荷载进一步增大，桩身的变形加大，土体由上至下逐渐发生屈服，水平荷载向更深层土体传递，桩周土体逐渐进入塑性阶段，位移变化速率逐渐提高.

2）桩顶水平荷载相同时，水平位移随溶洞数量的增多而增大.在水平荷载F=300 N时，A0桩桩顶水平位移值为6.967 mm；相比而言，A1桩桩顶水平位移值增大了3.70%，为7.225 mm；A2桩桩顶水平位移值增大了9.73%，为7.645 mm；A3桩桩顶水平位移值增大了21.26%，为8.448 mm.反过来也可以明显地看出，刺穿多层溶洞嵌岩桩的桩顶位移达到同一值时所需的荷载呈现规律性的变化.溶洞数量越少，桩顶所需荷载越大；溶洞数量越多，桩顶所需荷载越小.说明桩顶水平受拉时，刺穿多层溶洞嵌岩桩桩顶水平位移随桩身穿过溶洞数量的增多而增大，或者说，基桩水平承载力随桩身刺穿溶洞数量的增多而减小.

2.2 桩身侧向水平位移

桩身侧向水平位移（简称侧移或水平位移，下同）通过百分表测得，因嵌岩段桩身变形量较小，故只在嵌岩段桩身第1 个溶洞中心高度（与桩顶距离460 mm）处布置1 个百分表，该位置以下的侧移均未采集，其他百分表均匀布置在上层黏土层段桩身侧面，与桩顶距离依次为30 mm、93 mm、172 mm 和253 mm.图5 所示为各桩在各级水平荷载作用下桩身水平位移沿深度的分布曲线.由分析可知：

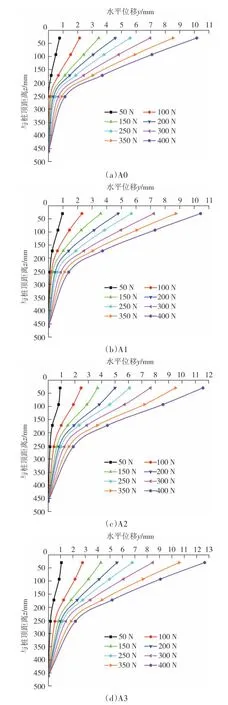
图5 桩身水平位移-深度曲线Fig.5 Relationship between depth and horizontal displacement of pile

1）桩身水平位移随水平荷载的增大而增大，随埋深的增大而非线性减小.侧移主要发生在上部黏土层，黏土层下部侧移较小，第1 个溶洞中心位置处，桩身侧移已基本为0.实际上，土岩界面的侧移也非常小.可以推理，桩身水平承载力主要取决于桩身上部土层参数.工程中，可以通过注浆法改善土质条件、提高基桩水平承载力.

2）水平荷载相同时，桩身水平位移随溶洞数量增多而增大.图示桩顶8 级水平荷载作用下，桩身相同位置处的侧移均呈现A3 最大、A2 次之、A1 再次之、A0 最小的规律.分析认为，溶洞数量影响了其顶部岩体的稳定性及桩身在水平荷载作用下的变形发展.

2.3 桩身弯矩

模型桩某一截面桩身弯矩M和对应的应变片数据ε满足下列关系式：

式中：E为弹性模量，Pa；I为惯性矩，m4；Δε为应变差值；D为应变片间距，m.

A0桩应变片与桩顶距离z依次为37 mm、177 mm、317 mm、342 mm、460 mm、640 mm 和820 mm，A1 桩应变片与桩顶距离z依次为37 mm、177 mm、317 mm、342 mm、410 mm、460 mm、510 mm、640 mm和820 mm，A2 桩应变片与桩顶距离z依次为37 mm、177 mm、317 mm、342 mm、410 mm、460 mm、510 mm、590 mm、640 mm、690 mm 和820 mm，A3桩应变片与桩顶距离z依次为37 mm、177 mm、317 mm、342 mm、410 mm、460 mm、510 mm、590 mm、640 mm、690 mm、770 mm、820 mm 和870 mm.将以上桩身各有效测点的应变数据代入式（3），即可得到水平荷载下桩身刺穿不同溶洞数量模型桩的桩身弯矩随深度变化曲线.4 根模型桩的桩身弯矩随深度的变化曲线如图6 所示.为了分析溶洞数量对串珠桩桩身弯矩的影响规律，做出水平荷载F=400 N 时4根桩桩身弯矩对比曲线，如图7所示.

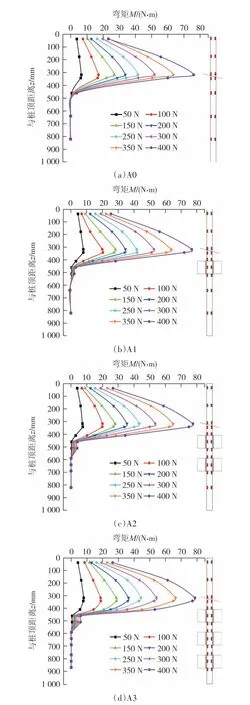
图6 桩身弯矩-深度曲线Fig.6 Relationship between depth and bending moment of pile

图7 F=400 N时桩身弯矩对比曲线Fig.7 Contrast relationship of pile bending moment when F=400 N

由分析可知：

1）在桩顶水平荷载作用下，桩身弯矩在土岩界面处和上层溶洞与底板界面处呈现2 个峰值，土岩界面处弯矩最大、截面最危险.A0、A1、A2和A3桩的M-z曲线整体呈抛物线形，随着深度的增大，各模型桩桩身弯矩呈现先增大后减小、上层溶洞与底板界面处再增大的发展趋势.桩身各截面弯矩随水平荷载的增加而增加，该规律与张浦阳等［7］对嵌岩桩水平承载力数值模拟取得的规律类似.工程中，建议加大土岩界面处桩身配筋率，并将桩身嵌入上层溶洞底板一定深度，防止基桩在土岩界面处发生弯曲破坏.

桩顶水平荷载作用下，桩身弯矩及其峰值随溶洞数量增多而增大，溶洞数量增多对桩身水平承载力不利.4 根桩弯矩峰值从大到小依次是A3、A2、A1和A0 桩，说明刺穿的溶洞数量越多，桩身越容易在岩土交界面处发生弯曲破坏.可以推理，在实际工程中，由于荷载很大，溶洞数量对桩身的影响更加显著.

2）桩顶水平荷载作用下，弯矩的变化仅仅影响到上层溶洞及其底板，第2 层溶洞及其以下的弯矩几乎为0.A1、A2和A3桩在上层溶洞位置处，桩体刺穿溶洞顶板进入溶洞内部，桩身弯矩迅速减小，桩体经溶洞空腔进入底板，此时桩身弯矩略有增大，在底板很快衰减到0.由此推理，在串珠状岩溶地区，桩身刺穿2 个以上溶洞时，加大桩长不能有效提高水平承载能力.

2.4 桩侧土抗力

桩侧土抗力通过土压力盒测得，土压力盒对称布置在离桩顶53 mm、133 mm、213 mm 和293 mm 位置处，各测点的土抗力p和土压力盒测得的微应变l满足下列关系式：

式中：pn表示第n个土压力盒的压力，kPa；l为微应变；a和b为土压力盒系数.

桩侧土抗力是桩-土相互作用的结果，刺穿多层溶洞桩顶部水平受拉时，桩在受拉方向发生位移，桩挤压土，土体对桩的位移产生约束，从而在桩身正面产生土抗力.埋设在桩侧的土压力盒测得加载过程中桩侧土抗力的变化如图8所示.

图8 各桩桩侧土抗力Fig.8 Soil pressure around piles

图8（a）表明，穿过土层的嵌岩桩承受水平荷载时，黏土层段桩侧土抗力沿深度先增大后减小，有1个峰值，土抗力呈“凸肚”形，随水平荷载增大而增大，与袁炳祥等［26］研究水平受荷桩-土相互作用得到的桩后土抗力规律类似.说明测试结果可靠.对于刺穿1个、2个、3个溶洞的桩，分析发现：

1）刺穿溶洞的桩侧土抗力曲线也呈“凸肚”形，土抗力沿深度先增大后减小，有1 个峰值.根据地基附加应力分布特点，最下方的土压力盒位置靠近岩土交界面，附加应力较小，桩顶位于土层面偏上位置，受到的附加应力为0，故在桩身中部附近一定会出现一个土压力峰值.土抗力与土压力沿桩身分布规律类似［27］.

2）桩顶水平荷载相同时，桩侧土抗力随溶洞数量的增多而增大，说明桩体刺穿溶洞数量越多，水平荷载下桩体侧移量越大，使得桩侧土抗力增大，因此，溶洞数量增多不利于桩身水平承载.

2.5 实测p-y曲线特征

刺穿多层溶洞桩顶部受拉时，黏土层桩身产生较大挠曲变形，嵌岩段桩身位移较小，因此本文仅对黏土层桩侧土抗力p和对应的桩身位移y进行分析.试验设计时，为避免土压力盒对位移测量的影响，未将水平位移测点与土压力测点设置在同一位置，故选取距离桩顶93 mm、172 mm 和253 mm 的位移测点作为第1、2和3计算点，利用MATLAB 软件对土抗力沿深度变化曲线进行三次样条插值，计算出对应测点的土抗力，作出A0、A1、A2 和A3桩3个测点处p-y曲线，如图9所示.

由分析发现：

1）刺穿多层溶洞水平受荷桩p-y曲线特征均与位置有关，位置越高，p-y曲线越容易收敛，相反，位置越低，p-y曲线变化率越大，越不容易收敛.说明刺穿多层溶洞水平受荷桩存在极限土抗力转折点深度.

2）刺穿多层溶洞水平受荷桩p-y曲线特征也与刺穿溶洞数量有关，A0、A1、A2 和A3 桩在相同位置的p-y曲线线型相同，但变化幅度不一样，随溶洞数量增加，p-y曲线更容易收敛，拟合后更能定量说明这一现象.

2.6 p-y曲线拟合

p-y曲线反映了单桩在水平荷载作用下，桩身产生水平位移时桩侧土对桩产生的土抗力，它受到桩身直径、刚度、桩土刚度比、桩顶荷载、溶洞数量等诸多因素的影响，目前已有多种拟合曲线方程.本文参考杨明辉等［28］p-y曲线方程，写出本文拟合曲线方程：

式中：pub表示桩周土的极限土抗力，kPa；y50表示土抗力为0.5pub时所对应的桩身水平位移，mm.

利用MATLAB 软件对实测p-y曲线进行双曲线拟合，根据Duncan-Chang 模型获得各测点的极限土抗力pub，进而通过三次样条插值得到各测点0.5pub对应的桩身水平位移y50.

将各桩身3 个测点处的土抗力除以pub，水平位移y除以y50，得到各级荷载下的数据，利用式（5），结合MATLAB 对测点数据进行拟合，选取最优拟合曲线作为最终p-y曲线拟合方程.α与β的相应取值见表2，拟合曲线见图10.

表2 p-y拟合曲线的α与β值变化Tab.2 Variation of α and β values of the p-y fitting curve

图10 p-y曲线拟合对比Fig.10 Comparison of p-y fitting curve

分析发现：

1）采用p/pub=α（y/y50）β拟合刺穿多层溶洞水平受荷桩在黏土层内的p-y曲线，效果良好.

2）参数α在0.007 4～0.147 9之间变化，参数β在0.016 8～0.498 5 之间变化.说明溶洞数量对α与β值变化幅度的影响较小，α与β值变化幅度体现p-y曲线随深度变化的敏感度，两者敏感度随溶洞数量增多而增大.

3 分析与讨论

为了深刻认识桩身串珠状溶洞数量对灌注桩顶部水平受拉特性的影响规律，对比不同岩土条件下桩顶承受水平拉力时的桩身响应，见表3.

表3 桩顶承受水平拉力时桩身响应对比Tab.3 Comparison of pile response with the top of the pile subjected to horizontal tension

桩顶承受水平拉力时，桩顶、桩底水平位移和桩身应变容易获得，可以根据弯矩分布和位移边界条件求算剪力、抗力、转角和水平位移分布.相比桩侧全为土体时，桩侧全为岩体时的桩身水平位移、桩身弯矩［12］和抗力分布规律相似，传递深度却要小很多.表3 显示，不同岩土条件下桩顶承受水平拉力时桩身响应有差异.桩侧全为土体时，桩身水平位移、桩身弯矩和抗力及其传递深度比嵌岩桩大很多.桩侧上段为土层、下段嵌岩时，不管桩身是否穿过溶洞，水平位移发生在上部土层，桩顶最大，入岩后趋0，弯矩在土岩界面呈现峰值，抗力在土层段随深度增大而增大.不同之处是，桩身穿过多层溶洞时，水平位移、弯矩和抗力均随桩身穿过的溶洞数量增多而增大，弯矩在上层溶洞与底板界面呈现第2 峰值.可以推理，在岩溶强发育区，灌注桩穿过第1 层溶洞进入底板一定深度后，再加大桩长对提高桩身水平承载力的贡献很小.

4 结论

对刺穿串珠状多层溶洞灌注桩的水平承载特性进行了试验研究，对比分析了各桩的水平位移、桩身弯矩、桩侧土抗力的分布规律以及p-y曲线特征，得到主要结论如下：

1）溶洞数量对水平位移具有显著的不利影响.上部土层段桩身水平位移随桩顶水平荷载增大而增大，嵌岩和刺穿溶洞的桩身水平位移很小甚至为0.桩顶水平荷载相同时，上部土层段桩身水平位移随溶洞数量增多而增大，单桩水平承载力随溶洞数量增多而明显减弱.

2）溶洞数量对桩身弯矩具有显著的不利影响.桩顶水平荷载作用下，M-z曲线整体呈抛物线形，桩身弯矩在土岩界面处和上层溶洞与底板界面处呈现2 个峰值，弯矩的变化仅仅影响到上层溶洞及其底板，第2 层溶洞及其以下的弯矩几乎为0.土岩界面处弯矩最大、截面最危险.桩顶水平荷载相同时，桩身弯矩及其峰值随溶洞数量增多而增大.

3）溶洞数量对桩侧土抗力具有显著的不利影响.土抗力沿深度先增大后减小，呈“凸肚”形，有1个峰值.桩顶水平荷载相同时，桩侧土抗力随溶洞数量的增多而增大.

4）刺穿串珠状溶洞的水平受荷桩p-y曲线特征与溶洞数量和位置有关.溶洞数量增加，位置越高，p-y曲线越容易收敛.可以采用p/pub=α（y/y50）β拟合土层段的桩身p-y曲线.溶洞数量对α与β值变化幅度的影响较小，α与β值变化幅度体现p-y曲线随深度变化的敏感度，两者敏感度随溶洞数量增多而增大.

5）工程桩刺穿串珠状溶洞时，为了提高单桩水平抗拉能力，建议采用注浆法改善上部岩土性质，加大土岩界面处桩身配筋率，并将桩身嵌入上层溶洞底板一定深度，防止基桩在土岩界面处发生弯曲破坏.