环境温度对混凝土梁式桥频率的影响研究

贺文宇 ，周磊 ，李志东 ，贺佳 ，户东阳

（1.合肥工业大学 土木与水利工程学院，安徽 合肥 230009；2.湖南大学 土木工程学院，湖南 长沙 410082；3.中铁二院昆明勘察设计研究院有限责任公司，云南 昆明 650200）

频率是桥梁的重要动力特性之一，由于其具有测量方便和精度高等优点，被广泛应用于损伤识别［1-3］.Cawley 等［4］采用损伤前后任意两阶频率变化的比值识别结构单处损伤.Rizos 等［5］利用子结构动力分析方法建立了频率与损伤的关系，进而根据频率定位和定量损伤.Khiem 等［6］推导了任意边界条件、带任意数目裂缝的梁频率与损伤的关系，并提出了相应的损伤识别方法.针对频率数据量偏少，而损伤识别是稀疏问题的特点，聂滋森等［7］和Hou等［8］基于稀疏正则化理论分别提出了悬臂梁和桁架的损伤识别方法.

然而，除损伤外，环境温度也会对频率产生较大影响［9-10］，其影响甚至会掩盖损伤导致的变化，影响损伤识别效果［11-13］.研究表明：环境温度引起的频率变化具有一定的规律［14］，可基于理论推导或基于数据建立环境温度和频率之间的对应关系来描述环境温度的影响.理论推导方面，王晶莹［15］和时玉平［16］将温度场转换成作用在梁两端的轴向偏心力，基于欧拉梁振动原理建立了简支梁自振频率表达式.陈雪松等［17］推导了考虑温度效应和剪切变形效应的改进型波形钢腹板组合箱梁的自振频率解析公式.王力等［18］提出了一种时变温度作用下考虑钢-混接触面滑移效应的新型波形钢腹板组合箱梁自振频率解析计算方法.目前基于数据的量化频率和环境温度的关系模型有：1）线性模型.Xia 等［19］对两跨混凝土板进行两年的连续监测，建立了频率和环境因素间的线性回归模型.Liu 等［20］对一座后张曲线混凝土箱梁桥的测试数据进行分析，建立了结构自振频率和温度的线性回归模型.Sun等［14］对连续梁桥和钢斜拉桥进行模型试验，建立了频率和温、湿度关系的多元回归模型.2）非线性模型.樊可清等［21］基于支持向量机建立了频率和温度关系的非线性模型.孙君等［22］利用236 d 的测试数据建立了润扬大桥频率日平均值与温度日平均值之间的六次多项式模型.Ding 等［23］利用润扬大桥的长期监测数据建立了温度和频率关系的多项式回归模型.3）学习模型.Hua 等［24］先对实测温度进行主成分分析获得主成分温度，并用于构建青马大桥频率与温度的支持向量机模型.Ni 等［25］基于青马大桥长期监测数据建立了温度和频率关系的基准神经网络模型.Zhou 等［26］选用桥梁不同部位测得的温度资料构造了平均温度、有效温度和主成分温度，分别以三类温度作为输入参数来构建神经网络模型.

上述基于理论推导的分析方法主要针对混凝土简支梁和波形钢腹板组合简支箱梁，且实施过程中需要桥梁的几何参数等信息；而基于数据的方法通常针对特定桥梁（结构），基于大量监测数据展开，其通用性受到了一定的限制.因此，从环境温度影响桥梁频率的内部机理出发，探明两者的内在规律，并建立具有通用性的环境温度-频率关系模型，对提高基于频率的损伤识别方法的有效性至关重要.

鉴于混凝土梁式桥是应用最广泛的桥梁类型，本文从环境温度影响混凝土梁式桥频率的机理出发，由频率解析式推导出温度作用下混凝土梁式桥频率的通用迭代公式，并通过数值算例和试验室试验验证迭代公式的有效性和适应性.

1 基本理论

环境温度对混凝土梁式桥频率的影响主要体现在改变材料弹性模量、边界条件、几何特性和产生轴向力，其中温度引起弹性模量变化对桥梁频率的影响最为显著［11，19］.温度影响混凝土的弹性模量，从而影响其刚度，进而影响频率.本节从梁式桥（简支梁和连续梁）频率的解析解出发，推导出温度作用下梁式桥频率的通用迭代计算公式.

基于欧拉伯努利梁理论［27］，等截面混凝土简支梁和两跨连续梁的第n阶频率分别为：

式中：fsn和fcn分别为简支梁和两跨连续梁的第n阶频率；m为梁单位长度的质量；L为单跨梁长；I为截面抗弯惯性矩；E为混凝土弹性模量；αn为各阶频率系数，分别为π，3.927，2π，….

综合式（1）和式（2），可得混凝土梁式桥频率简化通用公式：

式中：fn为梁式桥的第n阶频率；U为常数，由频率阶次和梁式桥类型确定.

对式（3）两边做微分处理可得：

假定温度变化微小，弹性模量随温度呈线性变化，材料弹性模量的热系数βE=，T为温度，材料线性膨胀的热膨胀系数为βL=，则：

式（9）表明频率相对变化率随温度变化的无量纲变化率为(βE+βL)∕2.混凝土和钢材的热膨胀系数分别为βLC=1.0 × 10-5∕℃和βLS=1.1 × 10-5∕℃，弹性模量的热系数分别为βEC=-3.0 × 10-3∕℃和βES=-3.6 × 10-4∕℃［24］.显然弹性模量热系数βE的绝对值远大于热膨胀系数βL的绝对值，因此温度引起弹性模量变化是改变频率的最主要因素，可得：

当已知温度T0及对应频率fn(T0)，此温度下频率温度曲线的斜率为k0=[βE·fn(T0)]∕2；从已知点(T0，fn(T0)) 开 始，以斜率k0构建在区间T0～T0+(ΔT)0的频率温度关系式，从而得到温度为T1=T0+(ΔT)0时所对应的第n阶频率为：

重复以上步骤，可以求得任意温度Tm=T0+下的频率fn(Tm)，即温度作用下的混凝土梁式桥频率通用迭代计算公式为：

当(ΔT)i取值不同时，所得频率精度不同，一般可取(ΔT)i=±1 ℃，从初始已知温度时的频率开始，由式（13）迭代计算至最接近目标温度的整数位，再取(ΔT)i=±0.1 ℃求得对应目标温度保留一位小数的位置，实现保证精度的前提下简化计算过程.

根据式（13）可知，采用该频率通用迭代计算无须采集全部温度时刻的频率数据，也无需桥梁梁长、截面特性和单位长度质量等参数，只需结合温度T0对应频率fn(T0)和此时的频率温度曲线斜率为k0，即可迭代计算获得梁式桥在任意温度下的频率.

2 数值算例

本节基于环境温度和弹性模量的关系建立不同温度时梁式桥的有限元模型，验证所提出的频率通用迭代公式.

欧洲规范CEB-FIP Model code 2010［29］规定：任意强度等级混凝土的弹性模量和温度的关系式为：

式中：E(T)为温度为T时混凝土的弹性模量.20 ℃时，C30 混凝土的弹性模量取3.0 × 104MPa，通过式（14）可计算得到任意温度下混凝土的弹性模量.

2.1 简支梁算例

图1 所示的20 m 标准跨径的混凝土简支梁，密度为2 600 kg∕m³，截面面积为0.472 5 m2，截面惯性矩为0.054 3 m4.通过调整混凝土弹性模量的方法建立温度作用下混凝土简支梁桥有限元模型，全梁划分为200 个等长欧拉梁单元.采用有限元模型在温度区间-10～50 ℃每隔5 ℃计算一次混凝土简支梁的前三阶频率，计算结果如表1 所示，绘制简支梁频率变化率-温度关系图，如图2 所示，其中图（a）、（b）和（c）分别为简支梁一阶、二阶和三阶频率与温度的关系图.20 ℃下的简支梁前三阶频率分别为4.518 Hz、17.666 Hz和38.408 Hz.相比于20 ℃时的相对变化率如表2 所示.结果显示：相对于基准温度，不同温度简支梁前三阶频率的相对变化率绝对值最大为4.49%，平均相对变化率为1.65%，表明温度通过改变弹性模量的方式显著影响简支梁频率，实际基于频率的损伤识别需要考虑温度的影响.

表1 数值简支梁频率计算结果Tab.1 Frequency of the numerical simply supported beam Hz

表2 数值简支梁频率相对变化率Tab.2 Relative change rate of frequency of the numerical simply supported beam %

图1 数值简支梁Fig.1 The numerical simply supported beam

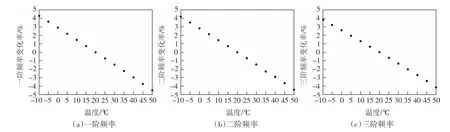
图2 数值简支梁频率变化率-温度关系图Fig.2 Relationship between frequency change rate and temperature of numerical simply supported beams

以20 ℃为初始温度T0，(ΔT)i取±1 ℃，采用迭代公式（13）计算相应温度时的混凝土简支梁前三阶频率，利用式（15）计算相对误差，结果如表3 所示.比较表2和表3可得：混凝土简支梁在温度作用下采用通用频率迭代公式计算的最大误差为0.741%，相比于相应温度下频率的相对变化率（最大4.49%）相对较小，前三阶频率的平均误差为0.105%，精度较高，可用于计算实际温度作用下的混凝土简支梁的频率.采用本文方法仍然存在一定的误差，主要是迭代过程中以折线代替曲线的累计误差.

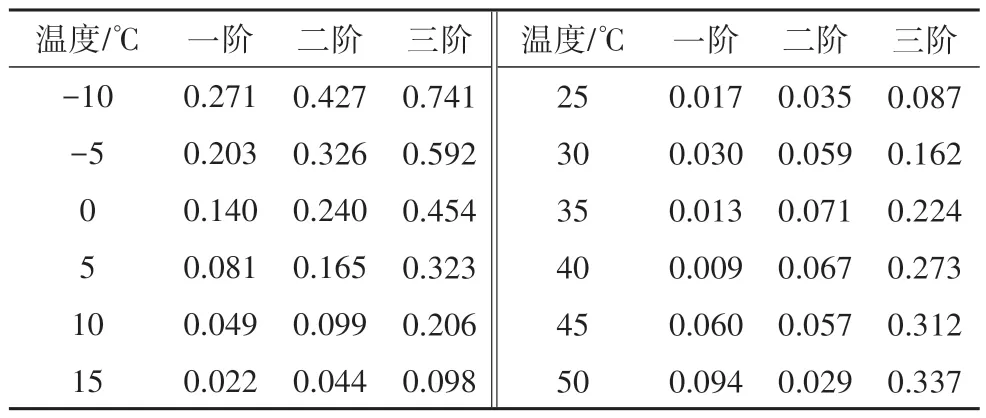
表3 数值简支梁频率相对误差Tab.3 Relative errors of frequency of the numerical simply supported beam %

式中：REf为梁频率迭代计算的相对误差；frefn和ficn分别为梁第n阶频率参考值和迭代值.

2.2 连续梁算例

如图3所示的两跨（2 × 20 m）C30混凝土等截面连续梁，截面几何参数和物理参数与第2.1节简支梁相同.将连续梁等分为40 个欧拉梁单元，采用与第2.1 节同样的方法和流程，在温度区间-10～50 ℃每隔5 ℃计算一次混凝土连续梁桥的前三阶频率，计算结果如表4 所示，并绘制相应的频率变化率-温度关系图（图4）.20 ℃下的连续梁前三阶频率分别为4.526 Hz、6.910 Hz 和17.882 Hz.相对于基准温度，不同温度下频率相对变化率如表5 所示，绝对值最大为4.35%，平均相对变化率为1.70%；通过频率迭代公式计算后的结果如表6 所示，最大误差为0.414%，前三阶频率的平均误差为0.079%.表明通用迭代公式能有效考虑环境温度对两跨混凝土等截面连续梁频率的影响.

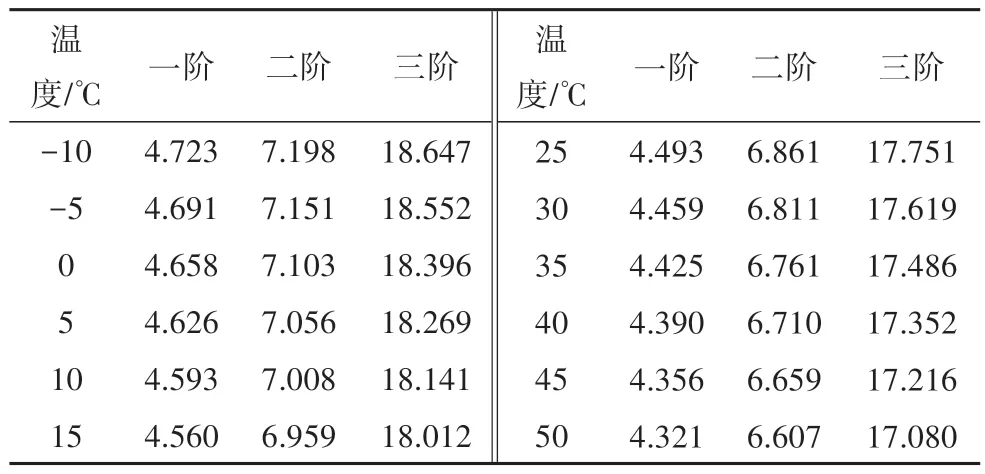
表4 数值连续梁频率计算结果Tab.4 Frequency of the numerical continuous beam Hz

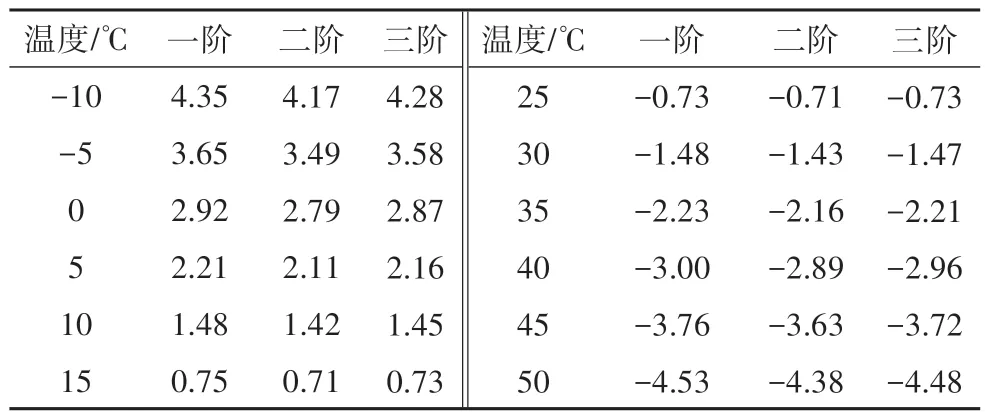
表5 数值两跨连续梁频率变化率Tab.5 Relative change rate of frequency of the numerical two-span continuous beam %

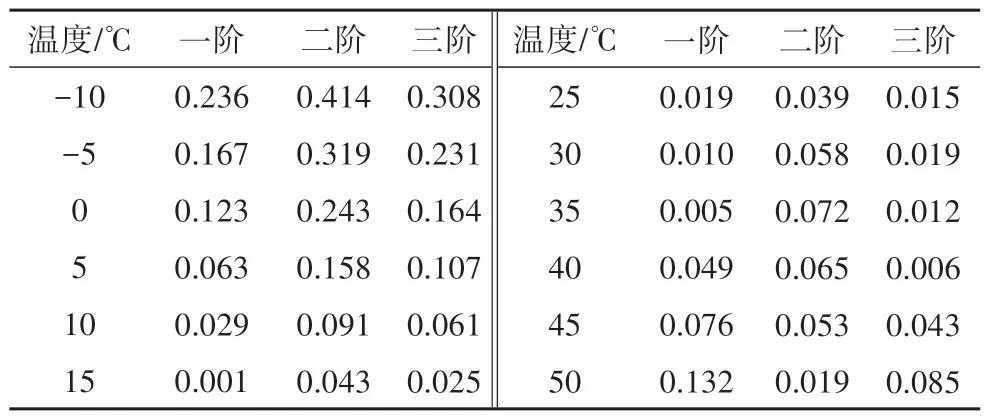
表6 数值两跨连续梁前三阶频率相对误差Tab.6 Relative errors of frequency of the numerical two-span continuous beam %

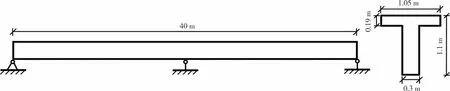
图3 数值两跨等截面连续梁Fig.3 The numerical two-span continuous beam with constant cross-section

图4 数值连续梁频率变化率-温度关系图Fig.4 Frequency rate-temperature relationship of the numerical continuous beam

实际上，变截面连续梁桥应用更加广泛，现以（10 m+16 m+10 m）的三跨变截面C30 混凝土连续梁桥为例，检验本文所提出的迭代计算公式对于变截面连续梁桥的适用性.三跨变截面梁总体尺寸、支点尺寸和跨中尺寸如图5 所示，中支点截面惯性矩为0.054 3 m4，截面面积为0.472 5 m2；跨中和边支点截面惯性矩为0.005 3 m4，截面面积为0.292 5 m2.将该梁等分为72 个欧拉梁单元，采用前述同样的方法和流程，得到前三阶频率（表7）和相应的频率变化率-温度关系图（图6）.20 ℃下的三跨连续梁的前三阶频率分别为5.688 Hz、10.982 Hz和15.121 Hz，不同温度下连续梁前三阶频率的相对变化率和通过通用频率迭代公式计算结果，分别如表8 和表9 所示.由此可见：本文提出的迭代公式对于不同梁式桥具有良好的适应性，且该频率迭代计算无须采集全部温度时刻的频率数据，基于少量的数据即可迭代计算获得梁式桥在任意温度下的频率.

表7 数值三跨连续梁频率计算结果Tab.7 Frequency of the numerical three-span continuous beam Hz

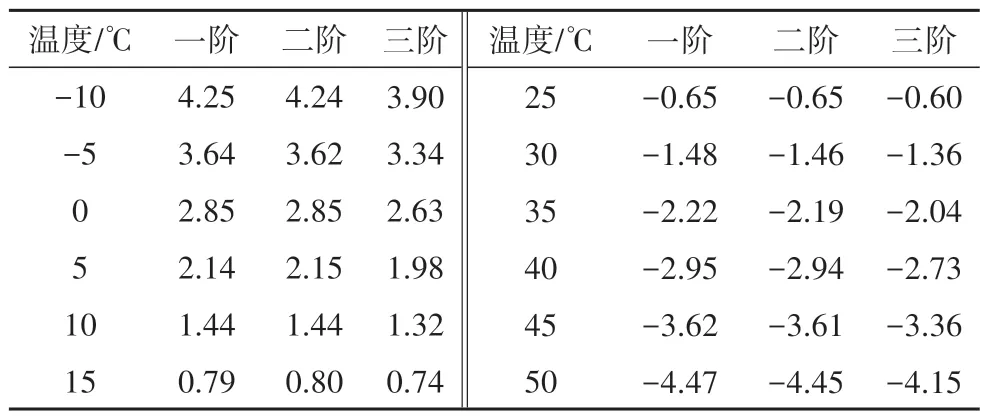
表8 数值三跨连续梁频率的相对变化率Tab.8 Relative change rates of frequencies of the numerical three-span continuous beam %

表9 数值三跨连续梁频率相对误差Tab.9 Relative errors of frequencies of the numerical three-span continuous beam %

图5 数值三跨变截面连续梁Fig.5 The numerical three-span continuous beam with variable cross-section

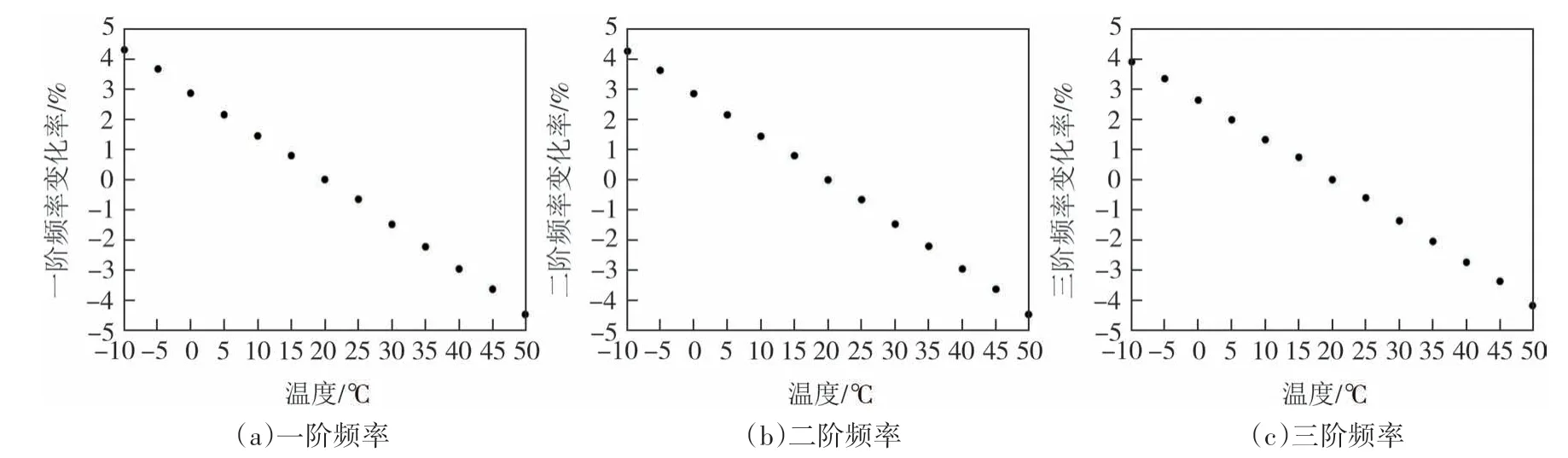
图6 数值三跨连续梁频率变化率-温度关系图Fig.6 Frequency rate-temperature relationship of the numerical three-span continuous beam

3 试验研究

3.1 试验过程

本试验在合肥工业大学结构实验室的环境耦合试验箱中进行，该试验箱可以模拟不同的环境温度，保温隔热性好，能保证箱内温度稳定，因此本试验中采用的是均匀温度，试验温度范围为-10～50 ℃.制作长4.2 m 的矩形截面C50 混凝土梁，具体参数：密度为2 688 kg∕m³，20 ℃时的弹性模量为34.5 GPa，截面尺寸为30 cm × 10 cm，惯性矩为2.5 × 10-5m4.在试验箱中分别搭建简支梁模型和连续梁模型，其中简支梁净跨径为4 m，连续梁净跨径为2 × 2 m，两端均各预留10 cm以放置支座，如图7所示.

图7 试验梁Fig.7 Experimental beam

本次试验分为四个步骤：

1）传感器布置.如图8 所示，简支梁底面等间距布置5 个加速度传感器，顶面等间距布置3 个热电偶；连续梁各跨底面等间距布置5 个加速度传感器，各跨跨中的顶面布置1个热电偶.

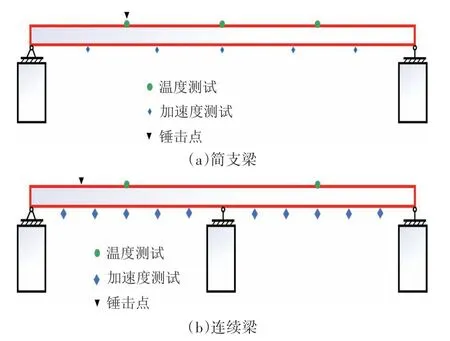
图8 试验梁布置Fig.8 The layout of the experimental beam

2）初始测试.将试验箱温度调至-10 ℃，稳定后开始试验.分别敲击简支梁1∕4跨梁顶中心位置和连续梁第一跨的1∕4跨梁顶中心位置，采集加速度信号，单次测试的采样时长为90 s，采样频率设为500 Hz.

3）重复测试.从-10 ℃开始升温，每上升3 ℃并且保持稳定时，重复上述试验，直至温度上升至50 ℃.典型的加速度响应如图9所示.

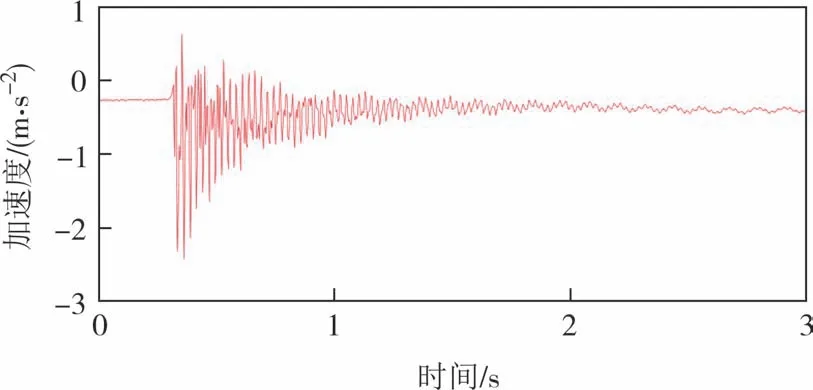
图9 试验梁典型加速度响应Fig.9 Typical acceleration response of the experimental beam

4）数据处理.对各温度下的加速度信号使用快速傅里叶变换识别试验梁的前三阶频率.试验简支梁和连续梁在各温度下的实测频率如表10 和表11所示.

表10 试验简支梁频率Tab.10 Frequency of the experimental simply supported beam Hz

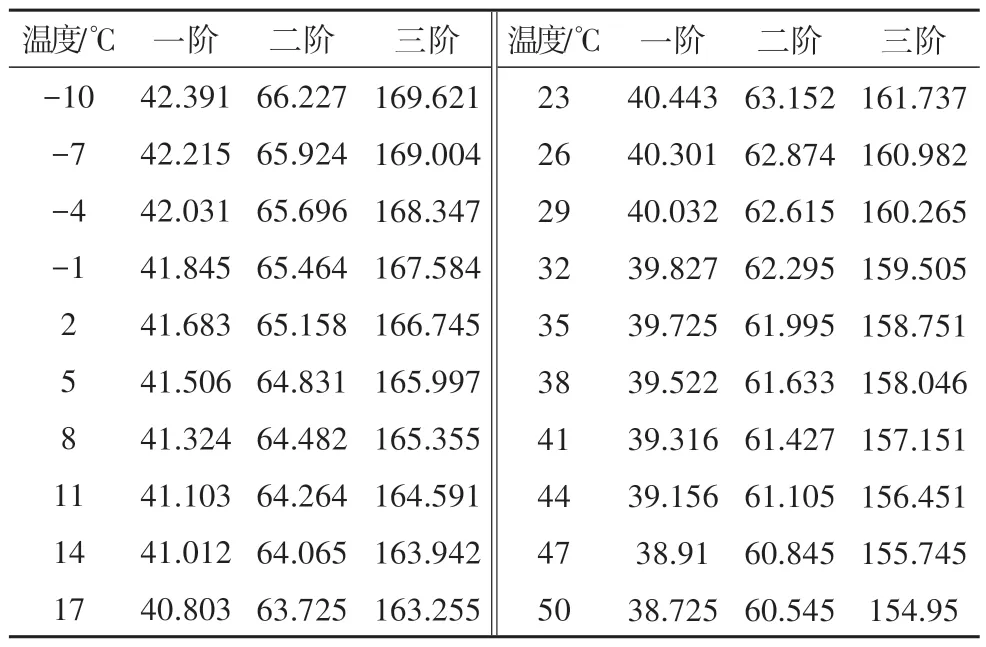
表11 试验连续梁频率Tab.11 Frequency of the experimental continuous beam Hz

3.2 结果分析

以20 ℃为基准，在-10～50 ℃每隔3 ℃计算一次试验梁的前三阶频率，频率变化率-温度关系如图10和图11 所示.相对于基准温度，不同温度下简支梁和连续梁前三阶频率相对变化率分别如表12 和表13 所示，相对变化率绝对值最大分别为4.66%和4.67%，平均相对变化率为2.48%和2.47%，表明温度显著影响梁式桥的频率，基于频率的损伤识别中需考虑温度的影响.

表12 试验简支梁频率相对变化率Tab.12 Relative change rate of frequencies of the experimental simply supported beam %

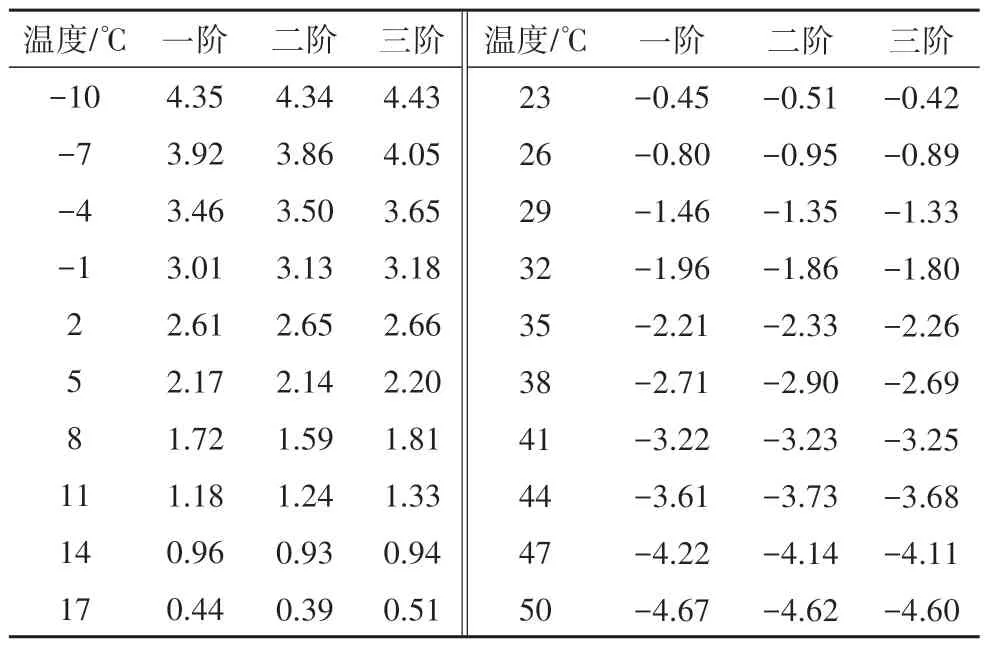
表13 试验连续梁频率相对变化率Tab.13 Relative change rate of frequencies of the experimental continuous beam %

图10 试验简支梁频率变化率-温度关系图Fig.10 Frequency change rate-temperature relationship of the experiment simply supported beam

图11 试验连续梁频率变化率-温度关系图Fig.11 Frequency rate-temperature relationship of the experimental continuous beam

以20 ℃时的前三阶频率实测值为初始值，采用通用迭代公式在-10～50 ℃每隔3 ℃计算一次试验梁的前三阶频率迭代值，利用式（16）前三阶频率迭代值和实测值的误差，结果如表14 和表15 所示.结果显示：简支梁和连续梁前三阶频率迭代公式计算的最大误差分别为0.268%和0.284%，相比于相应温度下的频率相对变化率（最大分别为4.66% 和4.67%）很小，前三阶频率的平均误差为0.074%和0.109%，表明在试验环境下本文所提出的梁式桥频率通用迭代计算公式准确可行.

表14 试验简支梁频率相对误差Tab.14 Relative errors of frequencies of the experimental simply supported beam %

表15 试验连续梁频率相对误差Tab.15 Relative errors of frequencies of the experimental continuous beam %

式中，RED为梁前三阶频率迭代公式计算的相对误差；Dic和Dmv分别为梁前三阶频率迭代值和实测值.

4 结论

混凝土梁式桥频率的变化可反映损伤情况，然而环境温度也会影响混凝土梁式桥的频率，进而影响损伤识别效果.本文从环境温度影响梁式桥频率的机理出发，由频率解析式推导出温度作用下混凝土梁式桥频率的通用迭代公式，并通过数值算例（等截面简支梁和连续梁、变截面连续梁）和环境耦合箱模型试验（等截面简支梁和连续梁）予以验证，主要结论如下：

1）该迭代公式无须采集全部温度时刻的频率数据，基于少量的数据即可迭代计算获得梁式桥在任意温度下的频率.

2）相对于基准温度，不同温度下数值梁和试验梁前三阶频率的最大平均相对变化率分别为1.70%和2.48%，环境温度对梁式桥频率的影响不容忽略，梁式桥频率和环境温度呈负相关.

3）通过本文提出的频率迭代公式计算的数值梁和试验梁前三阶频率的最大平均误差分别为0.117%和0.109%，所提出的频率通用迭代公式操作简单，具有良好的有效性和适用性，能有效考虑环境温度的影响，可用于计算实际温度作用下的混凝土梁式桥的频率.

温度荷载是桥梁的主要荷载之一，通常包括均匀温度和梯度温度，由于试验所用的环境试验箱只能模拟均匀温度，本文主要研究均匀温度的影响.事实上，梯度温度的影响将更为复杂，后续将进一步深入研究.