大跨度公铁双层斜拉桥主梁涡激共振机理与控制

2024-03-25刘志文周威刘振标严爱国夏正春陈政清

湖南大学学报（自然科学版） 2024年1期

刘志文，周威，刘振标，严爱国，夏正春，陈政清

［1.桥梁工程安全与韧性全国重点实验室（湖南大学），湖南长沙 410082；2.风工程与桥梁工程湖南省重点实验室（湖南大学），湖南长沙 410082；3.湖南大学土木工程学院，湖南长沙 410082；4.中铁第四勘察设计院集团有限公司，湖北武汉 430063］

为满足日益增大的交通量需求，亟需提升桥梁通行能力并节省线路资源.大跨度公铁合建双层桁架梁桥作为一种适用的桥型，其应用逐渐增多.随着桥梁跨径的增加，公铁合建桁架梁桥的结构刚度、自振频率和阻尼比显著降低，导致其对风荷载作用愈加敏感，易发生风致振动.涡振是在常遇风速下结构发生的一种风致振动形式，由流经结构后周期性脱落的旋涡引起，具有自激和限幅振动特性.当旋涡脱落频率接近或等于桥梁结构某一阶固有频率时，会引起结构共振［1］.尽管涡振不会像颤振一样导致发散性振动，但会影响行车舒适性，引发社会关注，若不进行控制还会导致结构疲劳.近年来，多座大跨度桥梁发生明显的涡激振动，如俄罗斯伏尔加格勒大桥［2］、韩国珍岛大桥［3］以及我国的浙江西堠门大桥［4］、广东虎门大桥［5-6］和武汉鹦鹉洲长江大桥等.与公路桥梁相比，铁路桥梁需保证高速列车平稳通过，对涡振更敏感.因此，大跨度公铁双层桁架桥梁涡振性能是桥梁设计中重点关注的问题之一.

传统单层桥面桁架主梁具有较好的涡振性能（如美国金门大桥、日本明石海峡大桥等），但已有文献研究表明，双层桁架梁的气动性能较复杂，存在涡激振动的可能性.王骑等［7］通过主梁节段模型风洞试验发现倒梯形双层桁架梁存在明显的竖向涡振，提出增设导流板来抑制涡振的方法；王景奇等［8］对双层桁架梁涡振性能及抑振措施进行试验研究，发现上层桥面栏杆透风率对涡振性能有较大影响；李加武等［9］通过主梁节段模型测振试验研究双层∏型断面的涡振性能，指出其涡振振幅随桥面间距的增加先减小后增大，并认为间距为梁高两倍时主梁涡振性能更优；Fang 等［10］通过试验研究发现双层桁架梁断面容易发生涡激共振，并通过计算流体动力学（CFD）数值模拟分析断面附近流场的频率特性，揭示主梁扭转涡振的诱因.此外，日本神户大桥［11］和我国重庆韩家沱长江大桥［12］也在原设计断面风洞试验中发现明显涡振现象.

目前，国内外学者针对单层桥面桥梁涡振性能及其控制措施开展较多研究.Nagao 等［13］通过烟雾法与测压法研究栏杆对箱梁涡振性能的影响，指出栏杆对控制主梁竖向涡振不利，但能抑制扭转涡振.李永乐等［14］通过试验发现检修车轨道和栏杆均对涡振有较大影响，认为分流板可以改善钢箱梁涡振性能.Wang等［15］、Larsen等［16］研究发现下斜腹板角度为15°时能显著提升流线型箱梁涡振性能.李春光等［17］通过大比例节段模型测振和表面测压试验，揭示栏杆基石对流线型箱梁涡振的影响，并指出降低栏杆基石高度和将其位置外移可有效抑制涡振.Yang等［18］研究下稳定板对箱梁断面涡振的抑制效果，发现一定高度、间距的双下稳定板可以消除主梁扭转涡振，并大幅降低竖向涡振振幅.此外，许多学者研究单层桥梁∏型断面的涡振性能.Kubo 等［19］基于测压试验探究∏型断面涡振机理.Zhang等［20-21］通过风洞试验对比多种气动措施对∏型双箱梁涡振性能的影响，认为在箱梁下缘增设小三角形风嘴的抑振效果较好.刘志文等［22］通过试验测试∏型断面涡振性能的影响，并比较采用上稳定板、下稳定板、导流板和裙板等抑振措施的效果.

采用CFD 进行主梁涡激振动研究具有流场可视化强等特点，广泛应用于桥梁风工程领域［23-26］.胡传新等［27］通过CFD数值模拟出加装抑流板后流线型箱梁附近的流场速度矢量图，揭示抑流板对涡振的控制机理.刘志文等［28］通过风洞试验与CFD 数值模拟从流场和表面压力变化的角度解释涡振机理，认为内移检修车轨道可有效抑制主梁涡振.李欢等［29］基于CFD 数值模拟探究∏型断面涡振机理.周志勇等［30］通过1∶20 大尺度节段模型风洞试验及CFD 数值模拟相结合的方法分析边防撞栏杆对桥梁涡振性能的影响.

综上所述，国内外学者研究主要针对单层桥面桥梁的气动性能，对公铁合建双层桁架梁桥涡振性能及其控制机理的研究相对较少.本文采用常规比例（1∶60）节段模型风洞试验研究不同来流攻角下双层桥面主梁涡振性能，并选取最不利风攻角综合比较间隔封闭栏杆、加装抑流板、增设倒L 型裙板和风嘴等气动措施对主梁结构涡振性能的影响.然后采用CFD 对比不同断面的静态绕流特性，从流场角度探究双层桥面桁架梁涡振机理.

1 概述

1.1 工程背景

洪奇沥特大桥是一座主跨808 m 的公铁双层斜拉桥，主桥结构的跨径布置为（100+100+100+808+100+100+100）m=1 408 m，立面如图1（a）所示.中跨处主梁采用上层正交异性钢桥面与下层钢箱梁组合的倒梯形双层桁架梁，上层公路桥桥面宽38.1 m，下层铁路桥桥面宽25.2 m，主梁中心处高度为15.32 m，上下弦杆中心间距为13 m，标准桁节间长度为13.5 m.斜拉索采用双索面扇形布置，在中跨主梁上的锚固间距为13.5 m.中跨主梁标准断面如图1（b）所示.全桥共224 根斜拉索，桥塔采用混凝土桥塔，塔高为258 m.

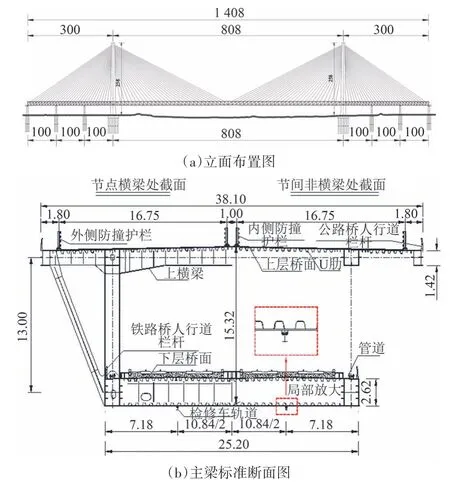
图1 洪奇沥特大桥立面布置图和主梁断面图（单位：m）Fig.1 Elevation layout and main deck section of hongqili bridge（HQL bridge）（unit：m）

1.2 结构动力特性

采用大型有限元商业软件ANSYS 建立该桥空间有限元模型，其中，桥面板采用SHELL181 单元模拟，钢桁架、桥塔和桥墩采用BEAM188 单元模拟；下层钢箱梁用BEAM188 单元模拟且与钢桁架之间用刚臂连接；刚臂采用BEAM4 单元模拟；栏杆、桥面铺装等模拟质量不考虑刚度贡献，采用MASS21 单元模拟；斜拉索采用LINK10 单元模拟.全桥共划分为13 734个单元.图2所示为洪奇沥特大桥主桥有限元模型（图中梁单元已显示单元形状）.有限元模型的边界条件与桥梁实际约束保持一致，即在桥塔和桥墩底部均设置为固结；在桥塔支座和主梁之间按照漂浮体系进行约束，同时在桥塔与主梁上层桥面连接处考虑水平抗风支座；在所有桥墩支座处约束竖向位移，并对一侧桥墩支座约束横向位移.在进行结构动力特性分析时，考虑初始应力和垂度效应，表1所示为该桥结构固有频率与振型描述.

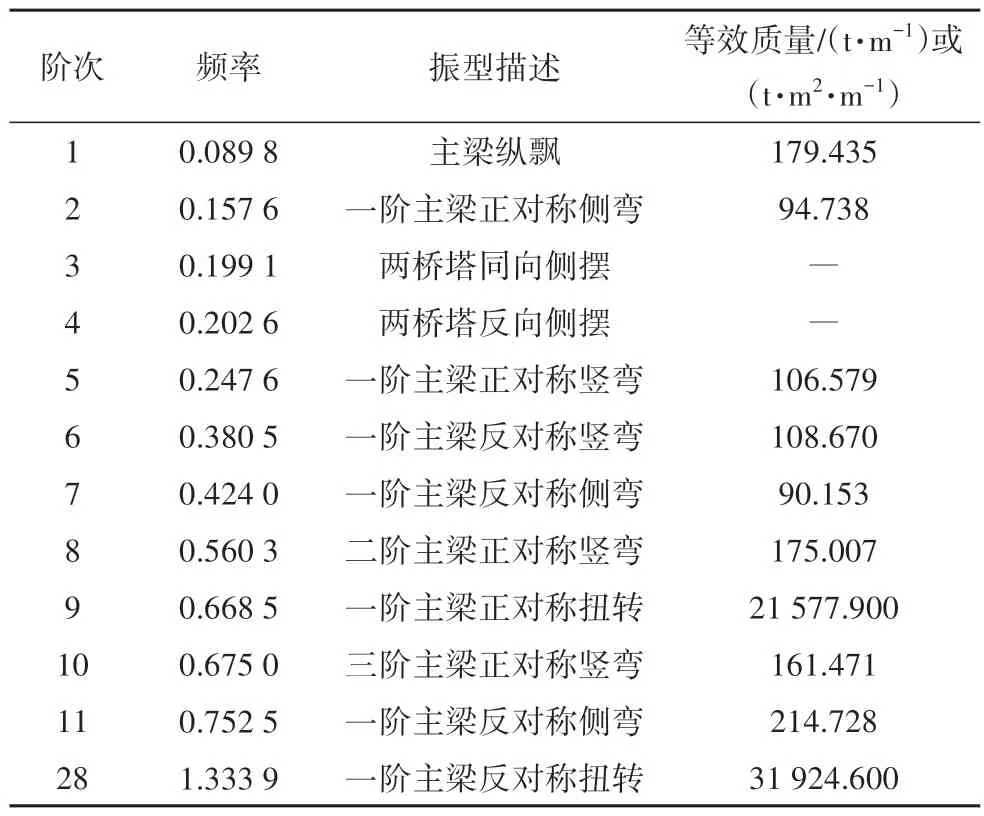
表1 洪奇沥特大桥主桥主要模态频率和振型Tab.1 Main modal frequencies and mode shapes of HQL bridge

图2 洪奇沥特大桥主桥有限元模型图Fig.2 Finite element model of HQL bridge

2 试验装置及工况

2.1 试验装置

洪奇沥特大桥主梁节段模型试验在湖南大学的HD-2号风洞第一试验段进行，该风洞为水平布置闭口回流式边界层风洞，试验段长17 m，宽3 m，高2.5 m，空风洞试验段风速范围为0～58 m·s-1且连续可调，风速大于2 m·s-1时来流湍流度小于0.5%.

桁架主梁沿顺桥向展向相关性较弱，为准确反应实际桥梁断面气动力性能，减少端部效应影响［31］，节段模型选取8 个标准桁段.综合考虑确定主梁节段模型的几何缩尺比λ=1∶60，长度为L=1.8 m，上下弦杆中心高度为H=0.217 m，宽度为B=0.635 m，模型长宽比为L∕B=2.83，具体参数如表2 所示.主梁节段模型采用钢骨架外包ABS 板制作，由钢骨架提供整体刚度，ABS 板外衣模拟主梁气动外形；桥面内外两侧防撞护栏及检修车轨道采用ABS 板雕刻，并模拟栏杆透风率.为形成二元流动，在模型两侧设置3 mm 厚类椭圆形端板，端板宽1.1 m，高0.7 m.模型两端连接水平连杆，在水平连杆端部共采用8 根竖向弹簧与风洞顶面和底面连接，形成两自由度弹性悬挂系统，并通过位于模型两端的转盘实现试验攻角改变.试验采用激光位移传感器进行测量，在模型中央下侧上下游对称布置两个激光位移计，位移计间距为0.345 m，采样频率为1 kHz.振动过程中模型未发生横向“跷跷板”现象.主梁节段模型风洞试验照片如图3所示，试验在均匀流场中进行.

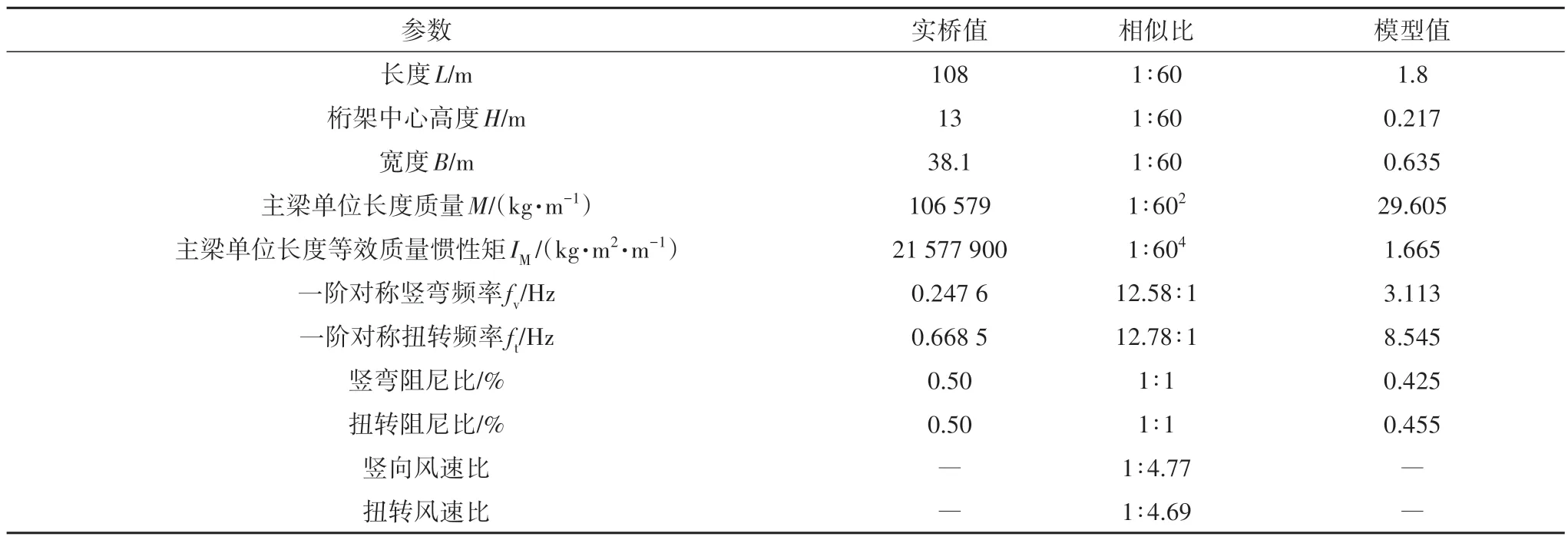
表2 成桥状态主梁节段模型试验参数Tab.2 Experimental parameters of the section model of the main deck in-service stage

图3 主梁节段模型风洞试验Fig.3 Main deck section model wind tunnel test

2.2 试验工况

首先，针对主梁断面原设计方案进行主梁测振试验研究；然后，针对最不利风攻角（+3°）进行主梁断面涡激共振气动控制措施研究.具体试验工况如表3所示，不同气动控制措施示意如图4、图5所示.

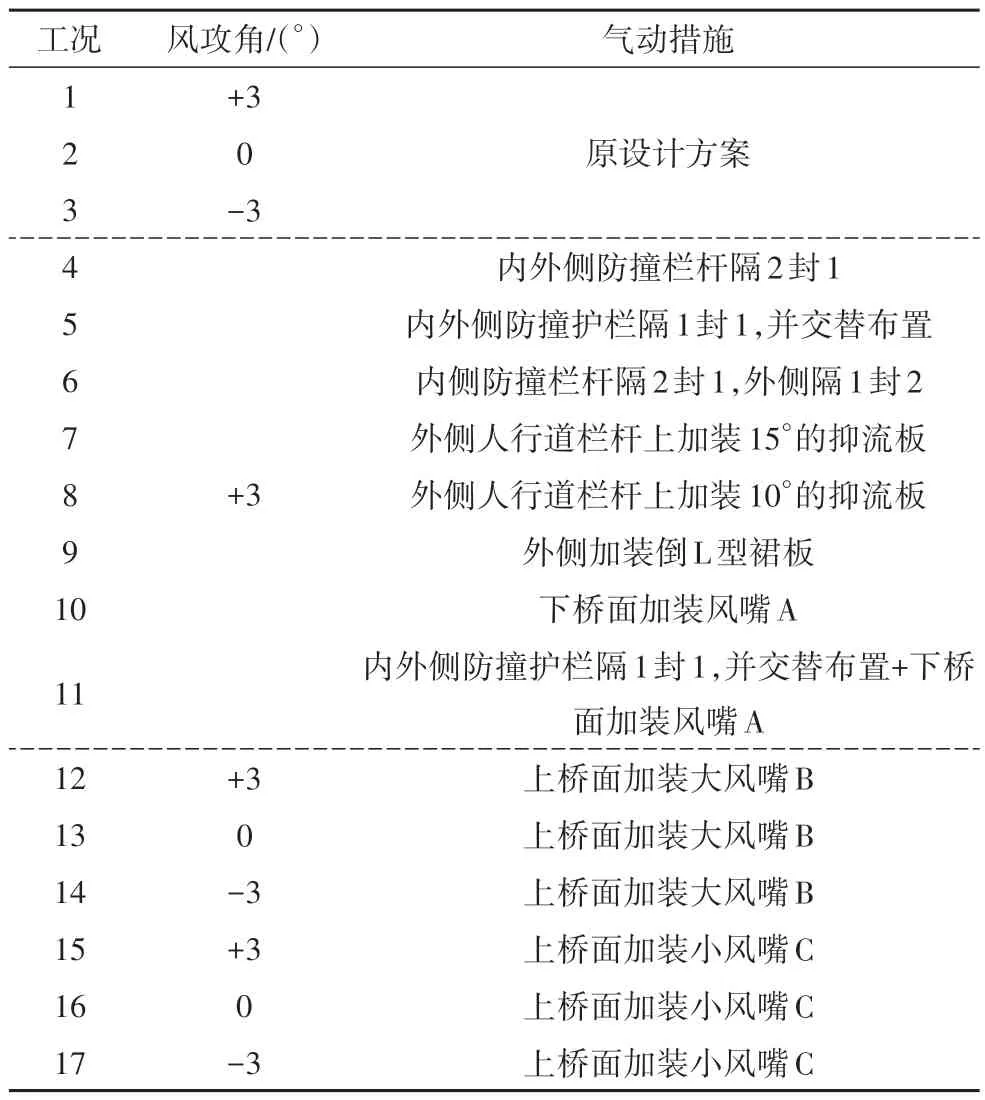
表3 试验工况汇总Tab.3 Summary of test cases

图4 气动措施位置示意图Fig.4 Aerodynamic measures

图5 气动措施实桥尺寸（单位：mm）Fig.5 Detailed dimension of aerodynamic measures of the prototype bridge（unit：mm）

3 试验结果

3.1 涡振允许幅值

公路桥梁和铁路桥梁对涡振限值有着不同的要求.由于列车行驶过程中对平稳性要求更高，铁路桥梁对涡振性能有更严格的要求.但目前铁路桥梁的抗风设计规范尚未颁布，因此桥梁的涡振允许值仍以公路桥梁的计算结果作为参考值.根据《公路桥梁抗风设计规范》（JTG∕T 3360-01—2018）第8.2.9 条规定，公路桥梁成桥状态主梁竖向涡激共振和扭转涡激共振的允许振幅分别为：

式中：[hv]和[θt]分别为主梁竖向和扭转涡激共振的允许振幅；fv和ft分别为主梁竖向和扭转振动频率；B为主梁断面的宽度.故主梁竖向涡激共振和扭转涡激共振的允许振动响应根方差分别为0.114 3 m 和0.126 6°.

3.2 主梁断面原设计方案涡振响应

图6 所示为主梁断面原设计方案涡振响应根方差随折算风速的变化曲线.其中，横坐标折算风速为U∕fB，U为风速，f取为零风速下的竖向振动频率fv或扭转振动频率ft，B为桥宽；纵坐标数据已换算到实桥，其中σv和σt分别为竖向和扭转振动根方差.由图6 可知，在+3°和0°风攻角下，主梁断面原设计方案均出现明显的竖向涡振和扭转涡振现象；在-3°风攻角下，主梁断面原设计方案仅有小幅竖向涡激振动，未出现扭转涡振现象.在+3°风攻角下，主梁竖向涡振包含两个锁定区间，折算风速分别是0.78～1.04（实桥风速为7.3～9.8 m·s-1）和1.50～2.28（实桥风速为14.2～21.5 m·s-1），对应的最大竖向涡振响应根方差分别为0.008 m 和0.271 m，其中第二个竖向涡振锁定区最大响应为规范允许值的2.37倍；扭转涡振的锁定区间为1.20～1.59（实桥风速为31.0～40.6 m·s-1），最大扭转涡振根方差为0.236°，为规范允许值的1.86倍.在0°风攻角下，主梁竖向涡振锁定区间为1.50～2.40（实桥风速为14.2～22.6 m·s-1），最大竖向涡振响应根方差为0.130 m；扭转涡振锁定区间为1.30～1.59（实桥风速为33.1～40.6 m·s-1），最大扭转涡振根方差为0.159°.在-3°风攻角下，竖向涡振锁定区间为1.10～1.27（实桥风速为10.4～12.0 m·s-1），最大竖向涡振响应根方差为0.036 m，未出现扭转涡振现象.

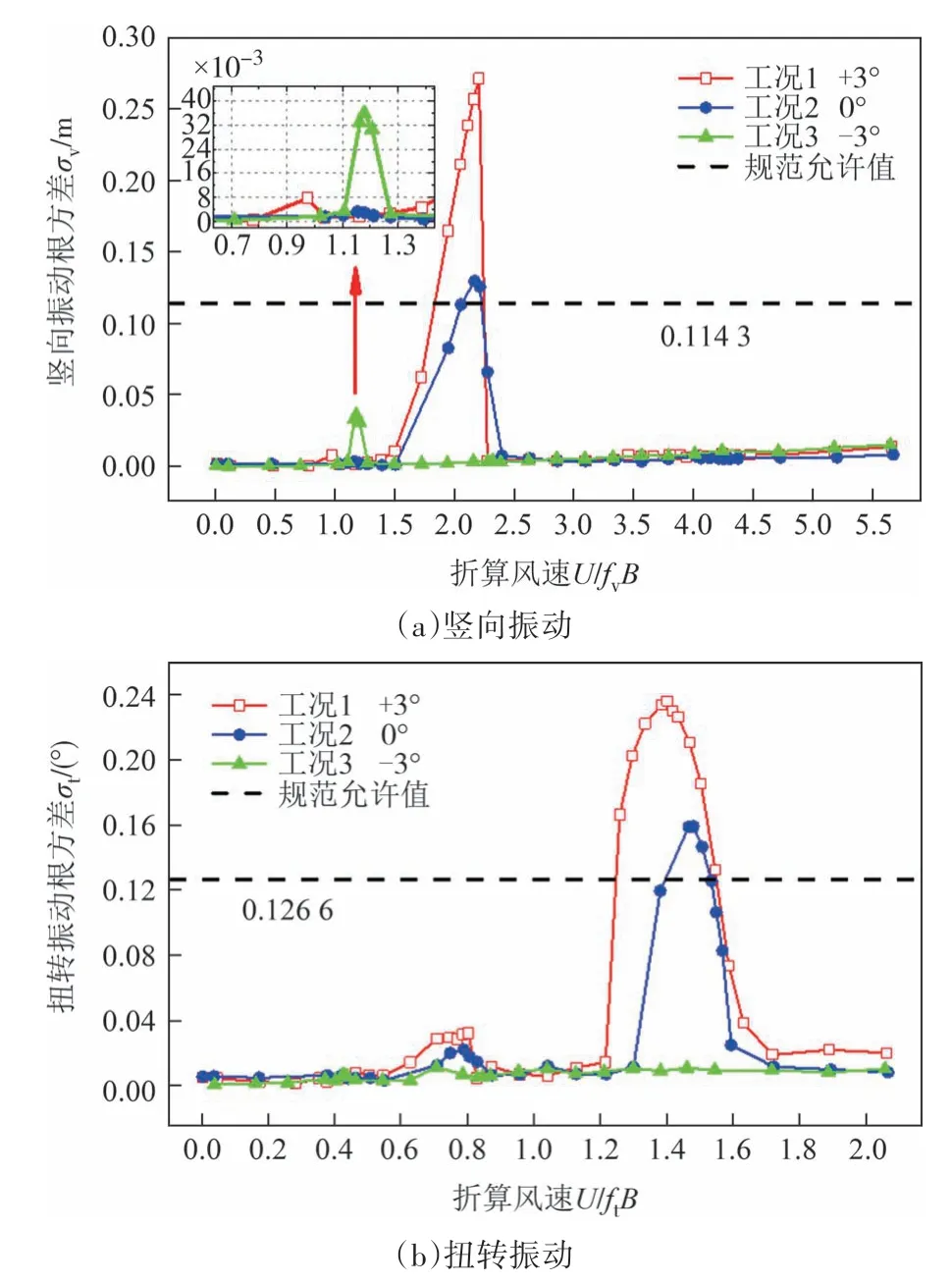
图6 主梁原设计断面涡振响应根方差随折算风速变化Fig.6 RMS of the VIV response of the original design section of the main deck vs.reduced wind velocity

在+3°和0°风攻角下，竖向涡振的锁定区间内同时出现小幅扭转振动现象［如图6（b）所示，对应折算风速为0.6～0.8］，但其根方差在允许值范围内.对折算风速为0.8时的测点位移时程进行频域变换，结果显示仅有频率为3.113 Hz 的主峰，这可能是由竖向涡振过程中模型连带产生的不规则振动导致，这一现象在以往文献中也有记录［17］.值得注意的是，在-3°风攻角下，主梁断面低风速下的竖向涡振响应明显高于其他风攻角，由于自然风的常遇风速以低风速为主，因此结构出现涡振响应的频率提高，对结构不利.

综上，主梁断面原设计方案存在较为明显的涡振现象，有必要进行气动控制措施研究.故选取最不利风攻角（即+3°风攻角）开展主梁涡振气动控制措施研究.

3.3 采取不同气动措施的控制效果

已有研究结果表明［28，32-34］，主梁断面涡振性能对其气动外形变化十分敏感，合理的气动措施可以有效控制涡振响应.因此，参照已有研究成果分别进行间隔封闭栏杆、抑流板、倒L 型裙板、下层桥面风嘴和上层桥面风嘴对主梁原设计断面涡振响应控制效果研究.

3.3.1 间隔封闭栏杆、加装抑流板

首先，研究3种间隔封闭栏杆方案和2种抑流板对主梁断面涡振响应的控制效果，分别对应工况4～8，气动措施详细尺寸如图5（a）（b）所示.试验在+3°风攻角下进行，图7所示为工况4～8对应的涡振响应根方差随折算风速的变化曲线.

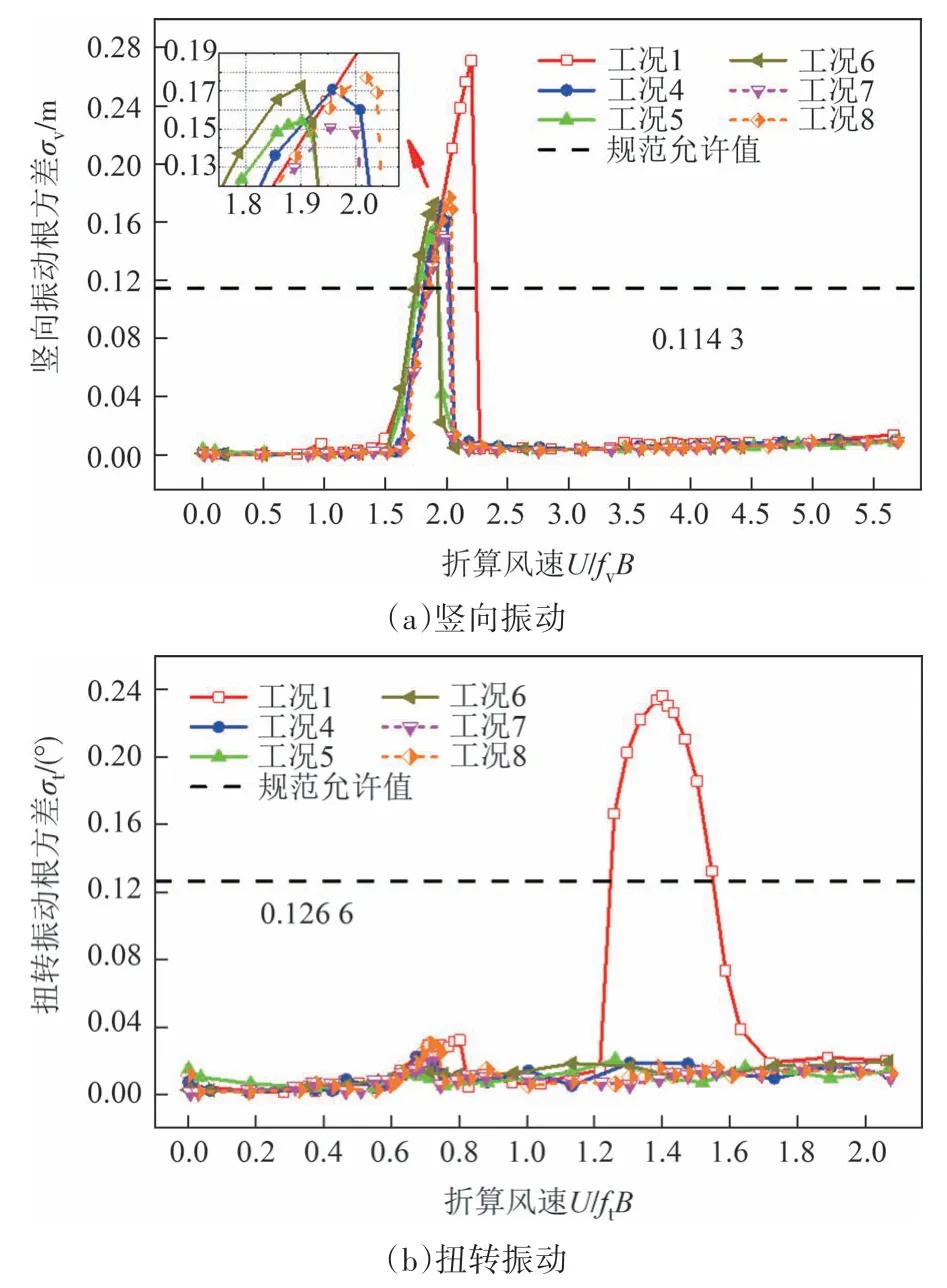
图7 工况4～8对应的主梁涡振响应根方差随折算风速变化Fig.7 RMS of the VIV response of the main deck vs.reduced wind velocity for cases 4～8

由图7可知，在+3°风攻角下，上层桥面上间隔封闭防撞护栏与加装抑流板对主梁涡振的抑振效果大致相同，均能完全抑振主梁的扭转涡振，并对竖向涡振控制具有一定的效果.其中工况5（内外侧防撞栏杆隔1封1，交替布置）与工况7（加装倾斜角为15°的抑流板）在同类型气动措施中对涡振的抑制效果相对最优，与原设计断面竖向涡振响应峰值相比分别降低43.2%和44.6%，但仍超过规范允许值.随着栏杆封闭程度与抑流板角度的改变，主梁扭转涡振性能均表现良好，而其竖向涡振性能会发生一定程度的波动.根据已有研究可知，间隔封闭栏杆可以减小上表面分离旋涡沿主梁纵向的相关性［35］，而抑流板尾部连续脱落的旋涡可以改变上表面气流的流动方式［27］.因此，两种气动措施可能扰乱了流经上层桥面上表面的气流，使分离后旋涡的能量分散，从而一定程度上减少主梁竖向涡振响应，并抑制主梁扭转涡振.

3.3.2 增设倒L型裙板、风嘴A和风嘴B

图8所示分别为工况9～12对应的主梁涡振响应根方差随折算风速的变化曲线.由图8 可知，在+3°风攻角下，上弦杆外侧增设风嘴B（角度为60°，工况12）的抑振效果相对最好，能完全抑制主梁的竖向和扭转涡振，其中较低风速下的第一个竖向涡振也完全消失；组合气动措施（工况11）的抑振效果次之，在折算风速1.62～1.96（实桥风速15.3～18.6m·s-1）范围内仍存在竖向涡振现象，其最大竖向涡振响应根方差为0.053 m，满足规范要求；而上弦杆外侧增设倒L型裙板（工况9）或下弦杆外侧增设风嘴A（角度为51°，工况10）后，主梁的涡振仅得到一定程度的抑制，其竖向和扭转涡振响应峰值仍超过规范允许值.另外，增设倒L 型裙板会使得主梁涡振区间整体后移.值得注意的是，倒L 型裙板和风嘴A 会导致主梁结构在低风速下的竖向涡振性能恶化，如+3°风攻角下，折算风速1.08（实桥风速10.2 m·s-1）附近的竖向涡振响应均达到原设计断面涡振响应的2.5倍，且较低的涡振起振风速会增加主梁涡振的出现频次，对结构不利.

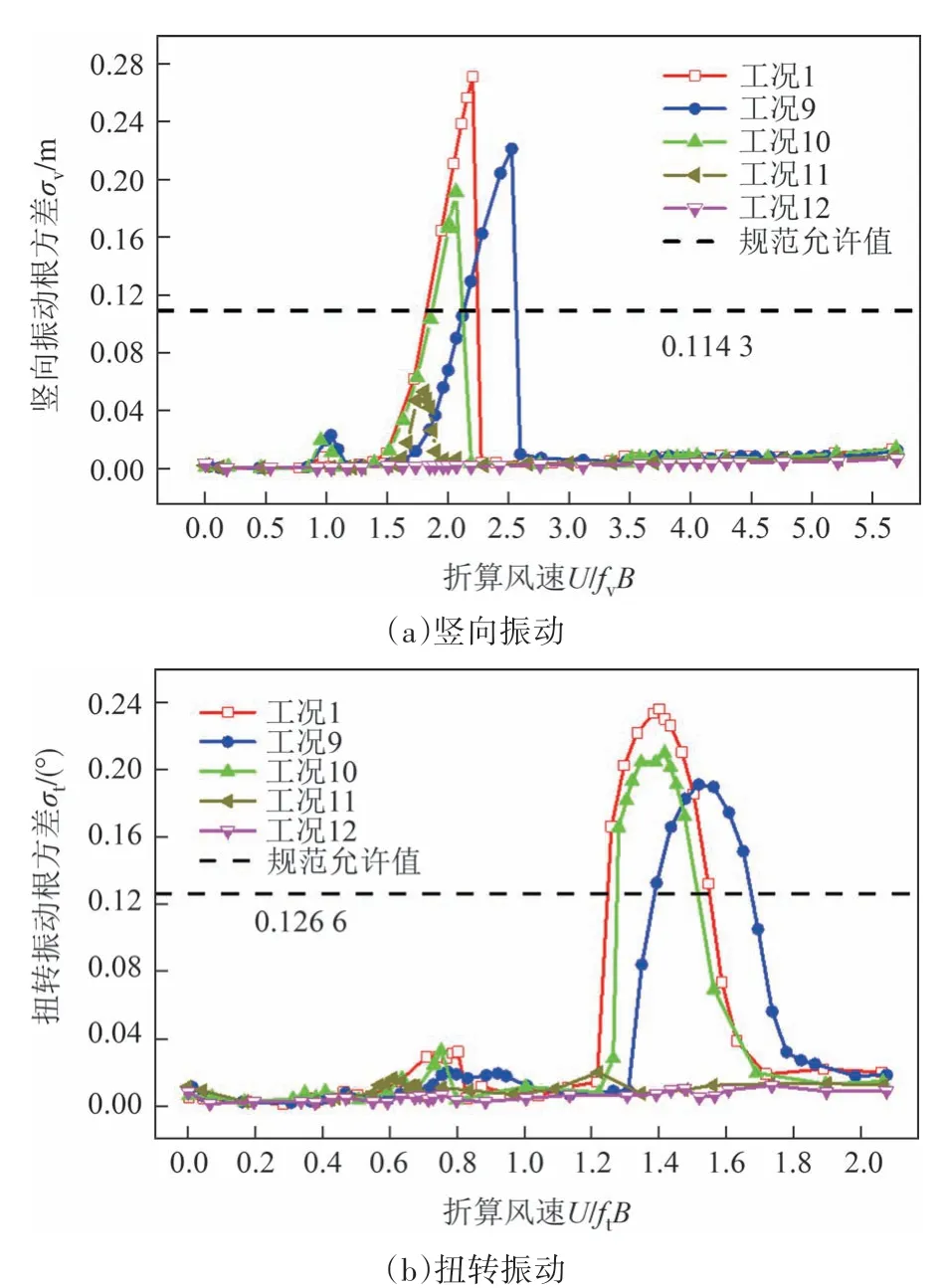
图8 工况9～12对应的主梁涡振响应根方差随折算风速变化Fig.8 RMS of the VIV response of the main deck vs.reduced wind velocity for cases 9～12

为全面评估上弦杆外侧增设风嘴B 这一气动措施的有效性，分别进行了0°、±3°风攻角下主梁结构涡振性能的试验研究，试验结果如图9 所示.由图9可知，上弦杆外侧增设风嘴B 后，各风攻角下主梁结构的涡振抑制效果显著提升，0°与+3°风攻角下均未发生涡激共振现象；-3°风攻角下，主梁断面仍有低风速区间的竖向涡振，但其最大竖向涡振响应较原断面减小76.7%，控制效果显著，未发现扭转涡振现象.这表明上弦杆外侧增设风嘴B 具有良好的抑振效果.

图9 工况12～14对应的主梁涡振响应根方差随折算风速变化Fig.9 RMS of the VIV response of the main deck vs.reduced wind velocity for cases 12～14

3.3.3 上弦杆外侧增设风嘴C

比较分析以上工况可知，在上层桥面上加装的气动措施对主梁涡振的影响效果更明显，如上弦杆外侧增设风嘴B 后能完全抑制主梁断面的竖向和扭转涡振现象；间隔封闭栏杆和增设抑流板均能完全抑制主梁断面的扭转涡振现象，且对竖向涡激的幅值和涡振区间有显著改变；而下弦杆外侧加装风嘴A 后主梁结构基本维持原有涡振风速区间不变.由此可以推断，上层桥面的涡脱对主梁涡振起控制作用.

考虑到上弦杆外侧增设风嘴B 后主梁结构具有良好的气动性能，为进一步检验上弦杆外侧风嘴对主梁结构涡振性能的影响，试验设计一种尺寸更小、外形更钝的风嘴C（角度为78°），详细尺寸如图5（e）所示.图10 所示为上弦杆外侧增设风嘴C 后不同风攻角下主梁涡振响应根方差随折算风速的变化曲线.由图10 可知，上弦杆外侧增设风嘴C 后，主梁结构在0°和+3°风攻角下的竖向和扭转涡振完全消失，在-3°风攻角下仅出现轻微的竖向涡振，且其幅值与增设风嘴B 后的响应幅值相当，最大竖向涡振响应根方差为0.010 m 左右，均远小于规范允许值，未发生扭转涡振现象.

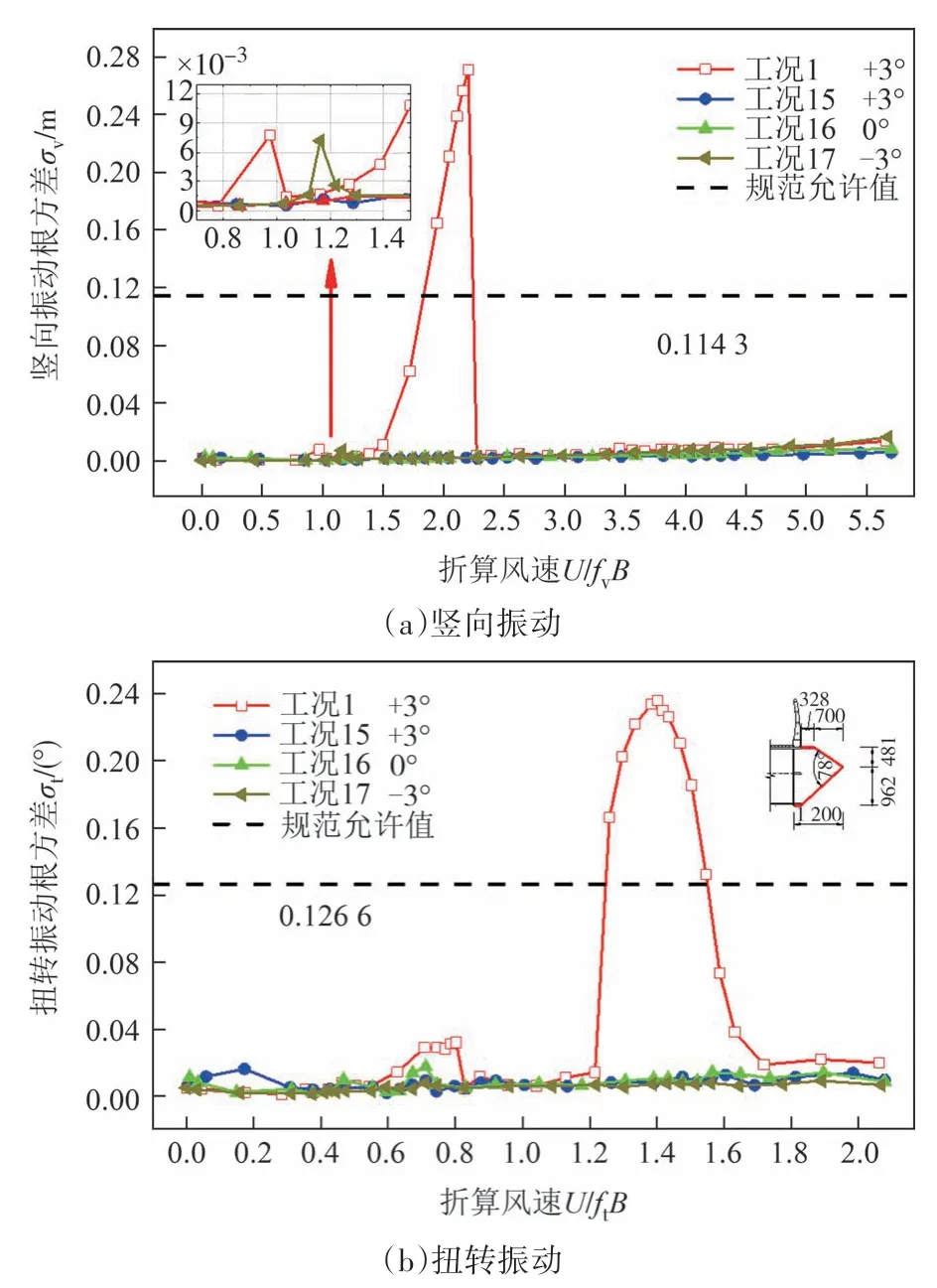
图10 工况15～17对应的主梁涡振响应根方差随折算风速变化Fig.10 RMS of the VIV response of the main deck section vs.reduced wind velocity for cases 15～17

对比图9 和图10 可知，风嘴B 与风嘴C 具有相同的抑振性能，均能有效抑制主梁断面的涡激振动，但风嘴C 的尺寸更小，经济性更优，因此风嘴C 更适合作为最终的抑振措施.

4 涡振机理

为进一步研究双层桁架主梁涡振机理，采用计算流体动力学方法研究主梁断面流场.综合考虑计算效率与计算精度，采用二维桁架断面进行CFD 数值模拟，偏于安全考虑将斜腹杆置于中间位置［36］，同时考虑钢桥面下方U 肋影响，简化后的二维计算断面如图11 所示.由于篇幅限制，数值模拟仅列出原设计断面与上弦杆外侧增设风嘴C 在+3°风攻角下的工况.

图11 主梁二维简化断面Fig.11 Two-dimensional simplified section of main deck

4.1 计算域与网格划分

计算域的选择与模型阻塞率δ有关，一般数值模拟要求δ＜5%.本文采用尺寸16B×32B（B为主梁宽度）的计算域，对应的模型外轮廓阻塞率δ=2.5%，计算域大小及边界条件设置如图12（a）（b）所示.

图12 计算域、边界条件和网格Fig.12 Computation domain、boundary condition and mesh

采用分块化方式划分网格，靠近壁面处采用结构化网格并局部加密，利用混合网格进行过渡，最外侧采用结构化网格，最大网格增长率控制在1.15 以下，网格总数约85万，底层网格高度为2e-5B.计算断面如图11 所示，其缩尺比取1∶60，与节段模型尺寸一致.在+3°风攻角下计算，计算风速为节段模型试验中竖向涡振响应最大时风速，即V∞=4.36（实桥风速为20.8 m·s-1），计算稳定后壁面处的Y+值基本在3以下（，u*为壁面剪切速度；y为距离壁面的第一层网格高度；v为流体运动黏性系数）.收敛参数设置为1e-6，湍流模型选取k-ωSST 模型；采用SIMPLEC 算法求解压力速度耦合方程，对流项和扩散项离散均采用二阶迎风差分.

4.2 网格与时间步无关性检验

主梁断面静气动力系数的定义：

式中：CD、CL和CM分别为阻力系数、升力系数和扭矩系数；FD、FL和MT分别是主梁断面在风轴坐标系下的阻力、升力和扭矩；ρ为空气密度.

为验证数值模拟计算结果的准确性，首先进行网格无关性检验.通过改变底层网格的厚度，设置3套不同数量的网格进行计算，网格数量及计算结果如表4 所示，根据网格数量的不同，由低到高分别用S1、S2 和S3 表示，T0为无量纲时间步.从表4 可以看出，三套网格的计算结果十分接近，为兼顾计算效率和精度，选取S2进行后续计算.

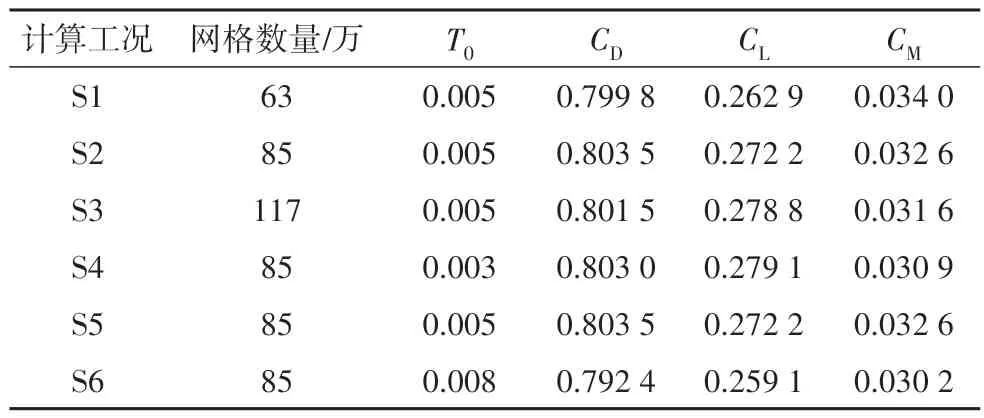
表4 主梁原设计断面三分力系数CFD结果Tab.4 CFD results of aerostatic coefficients of original design section of main deck

时间步无关性计算选取3 种不同的时间步长进行计算，时间步长由小到大分别用S4、S5和S6表示，计算结果如表4 所示.结果表明，改变计算时间步长对计算结果的影响较小，因此，为兼顾计算效率和精度，后续计算时取无量纲时间步小于0.005.

图13 给出主梁断面成桥状态三分力系数数值模拟结果与风洞试验结果.由图13 可知，数值计算结果与试验结果的变化规律基本一致，而数值模拟得到的阻力系数和升力系数略大于试验结果，这可能是由于CFD 计算是基于二维简化后的桁架断面，未能完全考虑实际三维桁架结构中各个构件间的干扰效应，导致各气动力系数间存在一定差异.总体上可以认为数值模拟的准确性得到保证.

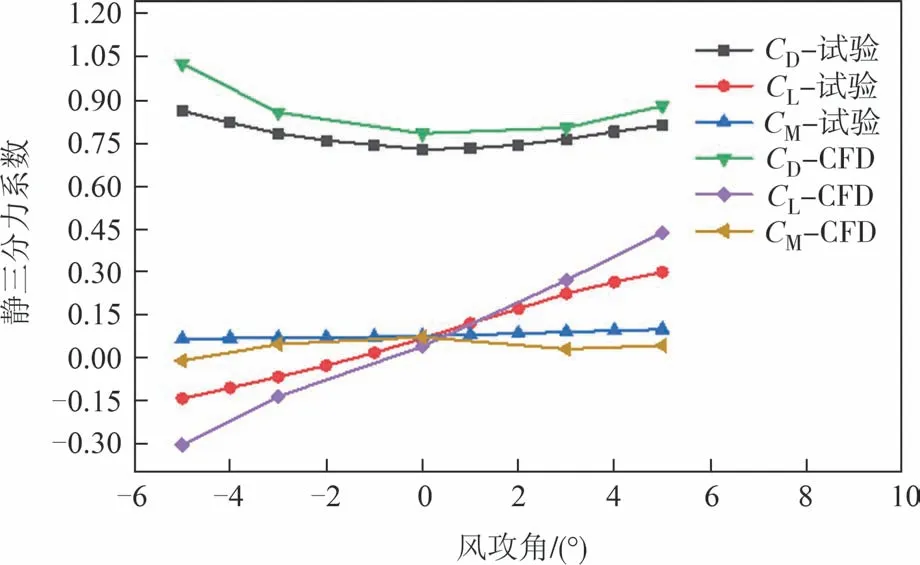
图13 主梁断面成桥状态静三分力系数试验与数值模拟结果Fig.13 Experimental and numerical results of aerodynamic coefficients of the main deck in-service stage

4.3 主梁原断面流场分析

图14给出了1个周期内不同时刻主梁原设计断面的瞬时涡量图，图14 中T为对应节段模型试验的竖向振动周期.由图14 可知，上层桥面和中间腹杆处均发生明显的旋涡脱落，其中大尺度旋涡主要聚集在上层桥面附近.当气流流经上层桥面迎风侧时，在其上缘人行道栏杆处分离并形成斜向上的运动气流，该气流受外侧防撞护栏阻碍减速后继续向下游运动，进而形成连续脱落的大尺度旋涡（图中用字母A 命名），脱落后的旋涡又再次附着于主梁中下部；同时，气流在上弦杆下缘也形成一系列周期性的旋涡脱落（图中用字母B 命名），其向下游移动时，受到风攻角和下层桥面“压缩作用”的影响，该旋涡紧贴下表面移动.故气流在上弦杆处发生规律性的旋涡脱落，脱落后的旋涡继续沿上层桥面上、下表面移动.根据胡传新等［27］、Larsen 等［16］的研究，发生竖向涡振的关键是：主梁上、下表面形成大尺度旋涡及其移动形成的周期性动力.因此，可以推断主梁的竖向振动与上层桥面的涡脱有关.

图14 主梁原设计断面瞬时涡量演化图Fig.14 Transient vorticity evolution diagram of the original design section of the main deck

此外，气流流经腹杆处时，在尾流区域形成典型的“卡门涡街”现象.由于旋涡对结构的作用力与其强度成正比，与距离的平方成反比［30］，而腹杆距离上下桥面较远且腹杆的尺寸较小，因此，腹杆尾部的旋涡对主梁影响较小.对于下层桥面，气流在其下缘分离后形成一段“回流区”，在断面尾部发生再附，由于气流流速较高，仅在尾流中形成旋涡；其上表面附近的流场可能受到上、下层桥面的“压缩作用”，边界层较薄，也仅在尾流中形成旋涡，未直接作用于下层桥面的上、下表面.因此，下层桥面不是引起主梁竖向涡振的原因.

4.4 气动措施抑制机理分析

采用4.1 节中的方法，对上弦杆外侧增设风嘴C后的断面进行CFD 静态绕流计算，计算参数与前面保持一致.图15 给出1 个周期内不同时刻增设风嘴C后断面的瞬时涡量图.

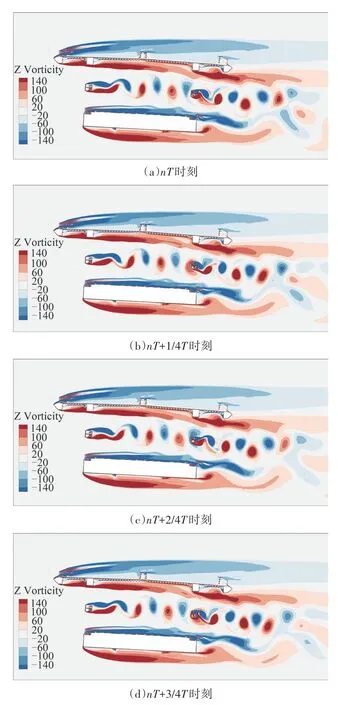
图15 增设风嘴C后主梁断面的瞬时涡量演化图Fig.15 Transient vorticity evolution diagram of the main deck section after adding the wind fairing C

对比图14 和图15 可知，增设风嘴C 后腹杆和下层桥面的静态绕流情况与原设计断面基本一致；但上层桥面上、下表面均没有出现周期性的旋涡脱落，且上表面出现一段完全覆盖上层桥面的“回流区”，即分离的气流没有在上表面发生再附.图16 是两种断面在某时刻下的瞬时速度云图，图中标记了距上层桥面中心0.05 m高（实桥3 m高）处的速度，由图可知，原设计断面在此处的风速为0.12 m·s-1，而增设风嘴C 后此处的风速为2.37 m·s-1，流速显著提高.故分析气流分离后没有附着于上表面的原因可能是：风嘴加快了上下表面的气流流速并减小气流分离的角度，使得气流流经人行道栏杆和防撞护栏后，仍有足够的动能向下游移动，故没有发生再附.