软黏土基坑开挖诱发邻近桥梁桩基的时变响应

应宏伟 ，熊一帆 ，吕唯 ，程康 ，刘广新 ，杜威

（1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2.浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058；3.中铁十一局集团有限公司，湖北 武汉 430061；4.浙江省铁投建设工程有限公司，浙江 温州 325000；5.杭州铁路设计院有限责任公司，浙江 杭州 310004）

在建、构筑物密集的地区开挖基坑将不可避免对邻近既有结构产生扰动，如房屋的沉降和不均匀沉降、隧道和地下管线的位移，严重时造成结构破坏.因此，准确预测基坑开挖诱发的邻近桥梁桩基变形具有重要的现实意义.

目前，研究基坑开挖对邻近桩基影响的方法大多为：1）理论解析法.Zhang等［1-2］建立了考虑变形耦合效应、界面剪切滑移特性以及受荷历史的被动单、群桩分析方法，认为竖直方向上桩身遮拦效应明显，而在土体刚度较大时可不考虑水平方向上的遮拦效应；程康等［3］利用两阶段法，基于推导的考虑土体非等量径向移动的坑外土体水平位移场和修正后的Pasternak 双参数地基基床反力系数，建立了基坑开挖下邻近既有单桩的变形控制方程；Liu 等［4］将基于Mindlin 位移解的坑外土体自由场视为外荷载施加于邻近桩基，将桩基视为放置于Vlazov 地基的Timoshenko 梁，考虑桩身的剪切特性和成层土的影响.2）模型试验法.Ong 等［5-6］基于一系列离心模型试验，详尽分析不同影响因素对临近软黏土基坑的单桩、群桩的影响；Ng 等［7-8］则利用离心机模型试验研究基坑开挖对邻近单桩、群桩和桩筏基础的影响，发现桩顶约束对桩身上部的附加弯矩影响显著，而对桩身下部附加弯矩的影响则相对有限.3）数值模拟法.Liyanapathirana 等［9］基于所建三维数值模型展开参数研究，开发出一套估算桩基变形和内力的设计图表；Shakeel 等［10］详细分析开挖深度、桩长、群桩位置、支护体系刚度、土体渗透性和既有荷载等因素对桩基性状的影响，发现开挖结束后坑外超静负孔压的消散会诱发桩基长期的沉降；Shi等［11］则利用数值软件对砂土基坑与摩擦桩的相互作用进行分析，认为若忽略开挖引起的桩侧和桩端摩阻力损失，桩基沉降将被低估高达39%；Soomro 等［12］重点分析开挖深度He与桩基长度Lp比例关系对桩基性状的影响，发现随着He∕Lp的增大，桩基沉降增大而侧移有所减小.

目前，“两阶段法”为理论研究的唯一方法，即先给出基坑开挖下桩基所在位置土体的自由位移场或应力场，再将其作为“外荷载”作用于桩基并计算力学响应.然而，囿于缺乏基坑开挖诱发坑外土体沉降的理论解，有关基坑开挖下邻近桩基竖向响应的理论研究停滞不前.此外，软黏土的变形和强度随时间发生明显变化的特性已在工程界达成共识，然而上述研究较少考虑基坑施工的时间效应，这将低估基坑开挖对周围环境如邻近桥梁桩基的影响.针对既有研究的不足，本文以深厚软黏土地基某下穿市域铁路桥梁的基坑工程为研究对象，利用PLAXIS 3D软件和软土蠕变模型建立三维数值模型，分析桥梁群桩的时效水平响应.结合两阶段法，将数值计算得到的土体自由场时变沉降作为“外荷载”作用于桩基，利用考虑桩土往返剪切的荷载传递方法，计算桩身自重、桩顶荷载和后续近接工程基坑开挖作用下桩基的竖向力学响应.

1 模型建立与验证

1.1 工程概况

温州某市政道路长线型基坑下穿市域铁路桥梁，桥梁正下方分坑如图1 所示.自上而下的主要地层分别为①淤泥、②粉质黏土和③黏土；基坑开挖深度为8.6 m，平面尺寸约39.2 m×36.0 m，采用放坡形式与相邻基坑连通；围护结构采用直径1 m、排距2.5 m 的双排桩结合两道支撑和被动区加固.限于篇幅，其他未见信息详见文献［13］.

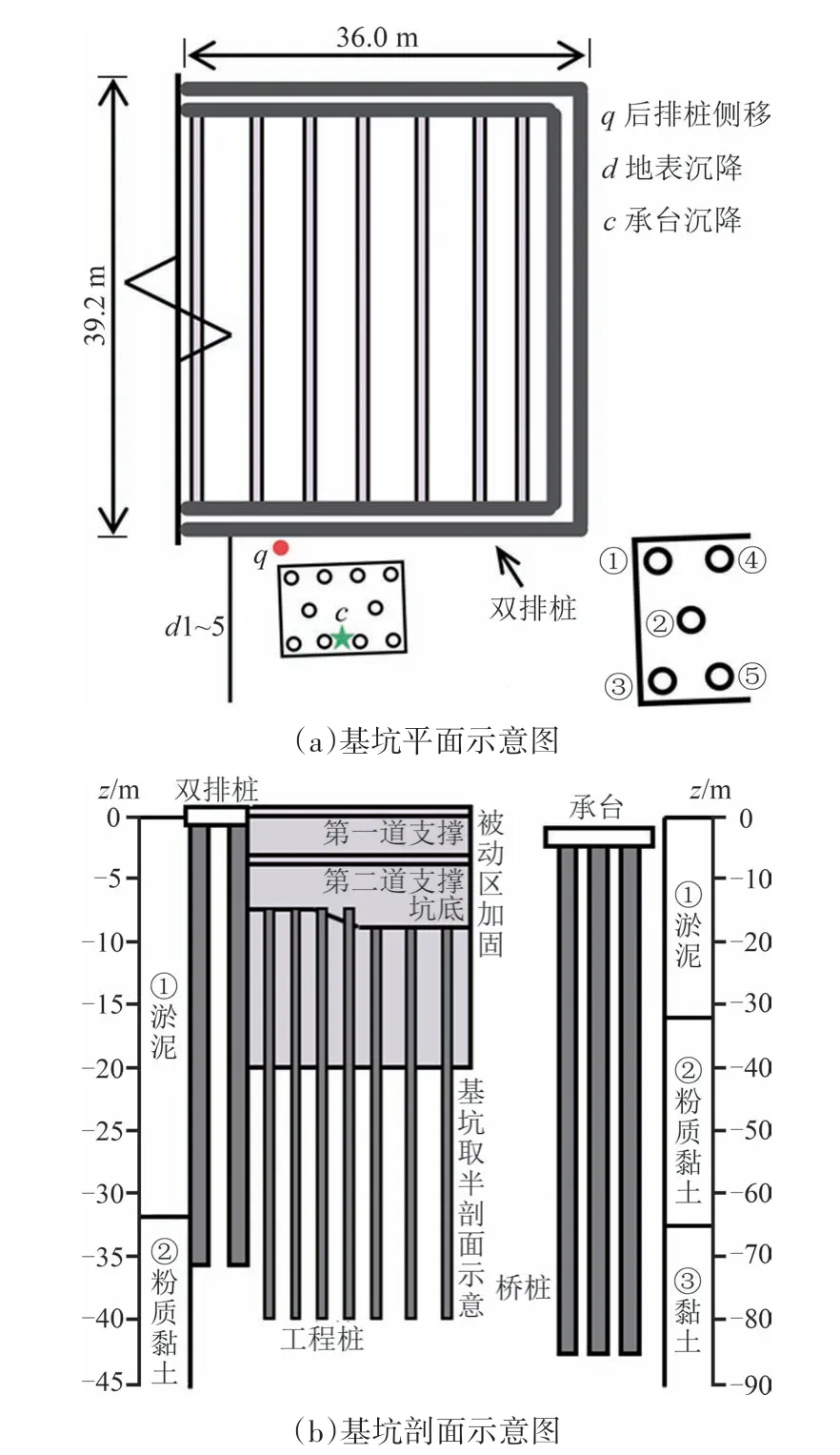
图1 基坑示意图Fig.1 Schematic diagrams of foundation pit

如图1 所示，基坑旁侧为桥梁桩基，距基坑最小间距仅1.9 m，采用桩长约81 m、直径1.2 m 的钻孔灌注桩，以③黏土为桩端持力层.

1.2 三维数值计算

采用PLAXIS 3D 有限元软件，考虑对称性，将前述分坑的1∕2作为三维数值分析的对象.为降低模型边界对计算精确性的影响，后排桩至水平边界的距离取大于5 倍开挖深度，竖向边界取至桥桩桩底以下约10 m，模型尺寸为100 m×100 m×90 m.计算模型设置下边界位移约束，上边界位移自由，水平边界水平方向位移约束，竖直方向位移自由；设置每个开挖步中临为空面孔压为零的边界面.

计算分析时采用的土体参数如表1 所示.虽然采用HS-Small 土体模型能够得到较为合理的墙体变形及墙后土体变形，但无法模拟土体的蠕变和应力松弛等流变现象.传统的观点认为，基坑工程属于临时性工程，在如此短的时间内，主固结尚且没有结束，次固结更是无从谈起.但是众多工程实践［14-15］表明深厚淤泥地基中的基坑在较短的开挖暴露期间变形明显增长，表现出很强的蠕变行为，这说明在基坑工程中土体的次固结可能与主固结同时发生甚至更为明显.为了考虑软土基坑施工的时间效应，选取软土蠕变SSC 模型作为①淤泥的本构模型；利用式（1）得到土体的修正压缩指数λ*［16］，修正回弹指数κ*和修正蠕变指数μ*则参考上海地区基坑分析的经验［17-18］，取λ*∕κ*=10、λ*∕μ*=20.②粉质黏土、③黏土和加固土则采用不考虑修正蠕变指数μ*的软土SS模型.

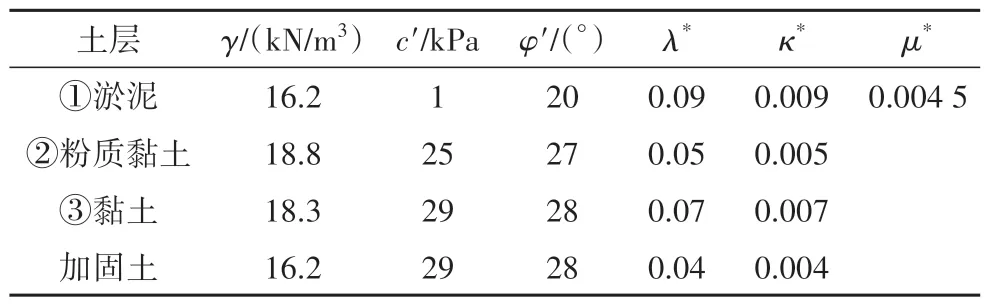
表1 土体计算参数Tab.1 Soils calculation parameters

式中：Cc为压缩指数；e为孔隙比.

数值计算模型中的结构参数如表2 所示，考虑坑底工程桩对基坑变形的积极作用［19］，对坑底工程桩进行建模；桥桩的侧阻力定义为土层相关，最大值取68 kPa，端阻力的极限取276 kN，取值依据详见后文.考虑桥梁桩基与承台的施工和上部荷载的作用，数值计算的模拟工况如表3 所示，将承台上部桥梁重量和市域列车行车荷载近似等效为5 500 kN 的集中静荷载作用于承台顶部.网格划分如图2 所示，生成84 244个单元、140 666个节点.

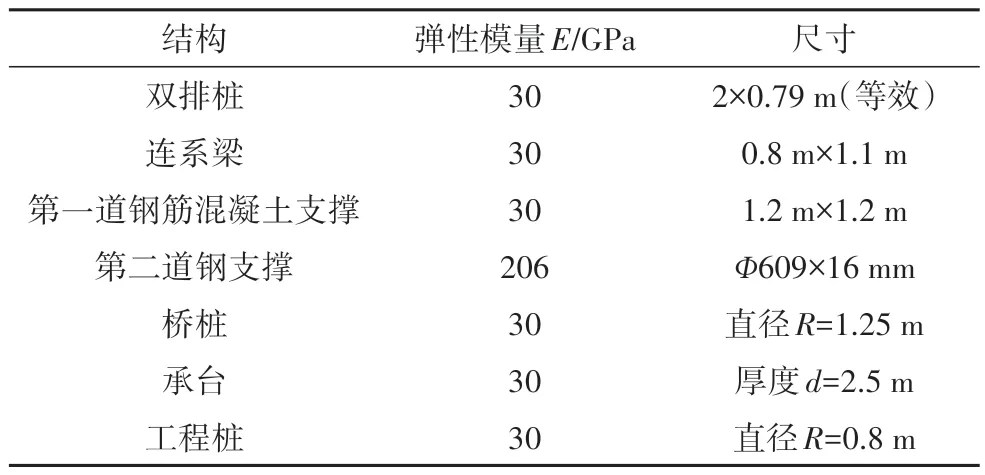
表2 结构计算参数Tab.2 Structural calculation parameters

表3 模拟工况Tab.3 Simulated stages

图2 网格划分Fig.2 Mesh division

1.3 模型验证

图3给出不同工况下基坑变形计算值与实测值的对比，其中δh为后排桩侧移，δv为地表沉降.由图3（a）可知，后排桩侧移计算值与实测值基本一致，但最大侧移所在深度大于实测值，这是因为本文案例利用墙后土体测斜表示后排桩侧移，而土体最大侧移所在深度随着与墙体距离的增大而减小［20-21］.比较图3（b）和表4 可知，无论是地表沉降还是承台沉降sc，计算值与实测值都较为吻合.有限元得出的坑外沉降槽收敛相对缓慢，是因为软土蠕变模型不能考虑坑外远端土体的小应变特性，表明该模型在分析坑外较远处的地表沉降时仍有局限性.总体而言，基坑水平位移和地表沉降的计算值与实测值吻合较好，可以认为建立的三维数值模型比较合理.

表4 承台沉降对比Tab.4 Comparison of cap settlement

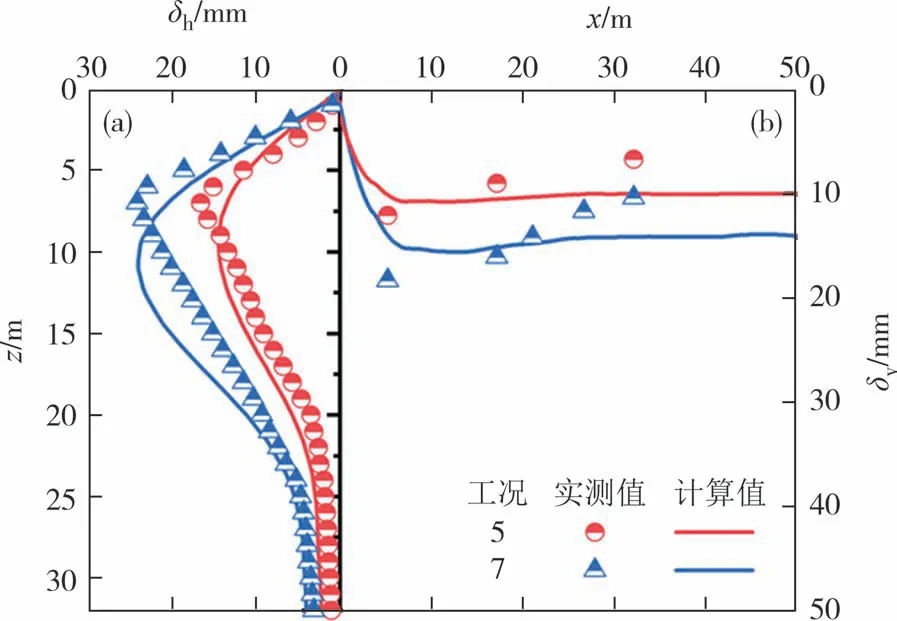
图3 基坑变形对比Fig.3 Comparison of excavation deformation

2 土体时变侧移下的桩基水平响应

数值计算中，引起邻近桥桩变形的因素包括基坑卸荷及其诱发的土体蠕变.为厘清土体蠕变对邻近桥梁群桩水平响应的影响，将SSC 模型退化为SS模型，并考虑桩顶约束条件，分析桥梁群桩的时效响应，如图4 所示.值得说明的是，SS 模型中的λ*和κ*分别对应HS-Small 模型中的Eoed和Eu［r16］，但无法考虑土体的小应变刚度；SS 模型模拟的是理想的开挖条件，即开挖与架撑瞬时完成，不考虑土体蠕变的影响.

图4 桥桩侧移与弯矩对比Fig.4 Comparison of lateral displacement and bending moment of bridge piles

由图4（a）（b）可知，土体蠕变不改变单桩之间的相对性状，但会显著影响群桩的整体侧移.这种影响的差异受施工时间的影响，由两部分组成.其一是蠕变引起围护墙的附加侧移从而诱发桥桩侧移；其二是蠕变诱发坑外桥桩产生不依赖于围护墙附加侧移的变形.比较非时效侧移和时效、非时效侧移的差值可知，对于深厚软黏土基坑来说，软土蠕变对坑外桥桩的影响甚至不亚于墙体瞬时变形，这说明在分析软黏土基坑时考虑蠕变效应是必要的.蠕变引起的邻近桥桩侧移在10 m（围护桩最大侧移所在深度）以上部分十分显著，在10 m 至36 m（围护桩桩底深度）则逐渐减小，这是因为10 m 以上的土体受开挖扰动的影响较大.由图4（c）（d）可知，土体蠕变会增大桩身的正、负弯矩，且近端桩基受到的影响更加明显.

桩身的变形和内力与单桩在群桩中的相对位置相关.近端桩桩身侧移和弯矩大于远端桩，角桩桩身侧移和弯矩大于中桩，这是因为近端桩所受士体运动的影响更大，角桩受遮帘作用的影响不如中桩.桩顶的变形和内力则受桩顶约束条件影响较大.关于承台约束情况，各桩桩顶弯矩并不为零，近端桩表现为负弯矩，图1（a）中的②号桩和远端桩表现为正弯矩.这是因为桩顶弯矩受单桩、承台相对位移的影响，开挖和蠕变引起的近端桩桩顶侧移大于承台侧移，承台侧移大于②号桩和远端桩的桩顶侧移，承台利用附加弯矩将近端桩向后拉，将②号桩和远端桩向前拽，这使得五根桩的桩顶侧移趋于一致，如图4（a）的实线曲线所示.对于自由桩顶情况，由图4（b）可知，当没有承台协调各桩桩顶之间的变形时，距坑壁越近，桩顶侧移越大.

3 土体时变沉降下的桩基竖向响应

PLAXIS 3D 软件中的Embedded pile 仅利用简单的弹性荷载传递方程模拟桩土相互作用，无法输入复杂的随深度变化的极限侧摩阻力，显然太过理想.因此，本文将数值计算得到的土体时效沉降作为“外荷载”作用于桥梁单桩，引入更合理的荷载传递方法，计算桩身自重、桩顶荷载和后续近接工程基坑开挖作用下桩基的竖向力学响应.

3.1 桩土相互作用

土体竖向位移场作用下的桩身沉降控制方程为：

式中：δp为桩身沉降；r0为桩基半径；τ为桩身任一深度处的侧摩阻力；Ep为桩体弹性模量；Ap为桩身横截面面积，γp为桩基重度.

对式（2）进行差分，得到任一节点i的差分方程：

式中：dl=Lp∕n，Lp为桩长，n为差分的单元数量.

考虑桩顶和桩端的边界条件，求解关于桩身位移的矩阵方程可得到桩顶加载和基坑开挖先后作用下的桩基沉降.考虑到荷载传递法应用的普遍性［2，22-23］，这里不详述有关桩身位移的求解过程.

对于受荷桩而言，其桩身荷载传递模型可以表示为如图5 所示的多段直线［23］，包括桩土关系的弹性、弹塑性、塑性阶段.

图5 桩侧三直线荷载传递模型Fig.5 Trilinear shaft mobilization model

τmax可以利用如下公式计算［2］：

式中：c、φ为土体的强度指标；k0为土体的静止侧压力系数；γ为土体重度；Rf为土体的破坏比.

斜率S1可以利用如下公式计算［2］：

式中：G为土体的剪切模量；桩的有效影响半径rm=2.5Lp（1-v），v为土体的泊松比.

桩端荷载传递模型如图6 所示［23］，考虑加荷段的方程为：

图6 桩端荷载传递方程Fig.6 Toe mobilization model

式中：qb为桩端反力；qb-max为桩端反力的极限值；Δδ为桩土相对位移标记为a；ΔδT为达到桩端反力极限值所需的桩土相对位移，取值可参考文献［24］.qb-max的计算式为：

式中：Nc、Nq为无量纲承载力系数，取值可参考文献［25］；pˉ为桩端平面侧边的平均竖向压力.

如图6（b）所示，利用斜率Rb描述卸荷条件下桩端应力应变的变化，其中加荷段以λ=1为例.值得注意的是，当桩端土体沉降大于桩端沉降时，桩端反力可忽略不计.

3.2 算例分析

同为温州深厚软黏土地区的世贸大厦有着详实的试桩资料［26］，结合文献［23］，表5 给出所需计算参数.

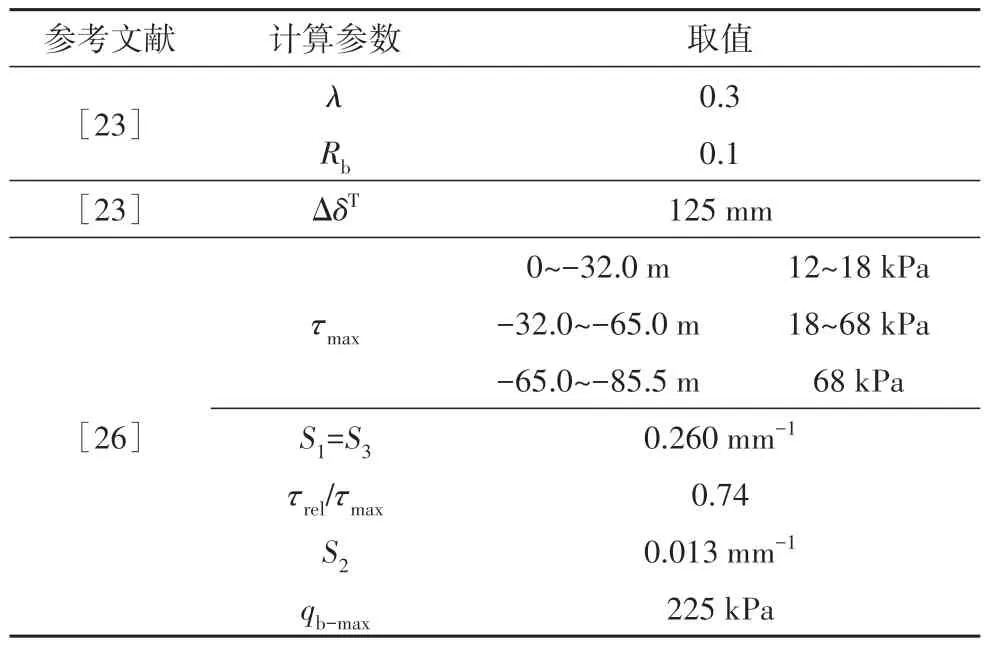
表5 计算参数Tab.5 Calculation parameters

利用表5 中的计算参数，考虑单桩重度的影响，图7 给出图1（a）中②号桩的荷载-沉降曲线，其中F为桩顶荷载，sp为桩顶沉降，加载包括桩基在自身重度和桩顶荷载作用下的竖向应力平衡.进一步将桩基受力分为两个过程，首先利用数值模型中②号单桩在工况3 下的桩顶轴力作为桩顶荷载，计算竖向力学响应；其次，将数值模型中②号单桩处的自由时效沉降作为“外荷载”作用于桥梁单桩，计算结果如图7 所示.值得说明的是，由于本文算例变形较小，桩土状态位于弹性区间，因此理论值与有限元计算结果基本一致.

3.3 参数分析

本文算例具有典型性，一般临近市域铁路桥梁的市政道路基坑挖深较浅且围护刚度足够大，同时考虑到本文算例位于深厚软黏土地基且邻近桥桩距基坑较近，因此粗略认为图7 中作为“外荷载”的时效沉降可作为其余案例沉降的保守估计，不对其展开讨论.

图8 给出了不同直径的桥桩在加载和开挖往返剪切作用下的竖向响应对比，其中L为桩顶至计算点的距离，N为桩基轴力.由图8（a）可知，桩基沉降随直径的增加而减小，但当桩基直径超过1 m 后，继续提高直径对减小沉降的帮助极为有限.观察图8（b）（c）可以发现，加载阶段大直径桩基的轴力先增大后减小，表明自身重度对变形控制不利；开挖诱发桩基上部的负摩阻力，导致轴力随深度的增大先增大后减小；开挖后的轴力随桩径的增大而增大，且变化速率逐渐增大.事实上，对于灌注桩而言，孔径越大，侧壁土的应力松弛越严重，k0越小，对于侧摩阻力的削弱也就越严重；不仅如此，桩基的极限端阻力随桩径增大呈双曲线减小［27］.可见，对于桩顶承受荷载不大且后续受近接工程基坑开挖扰动不大的深厚软弱地层中的桥桩桩基，在以桩顶变形为控制目标时，存在一个合理桩径，盲目增大桩径并不是一个好的选择.

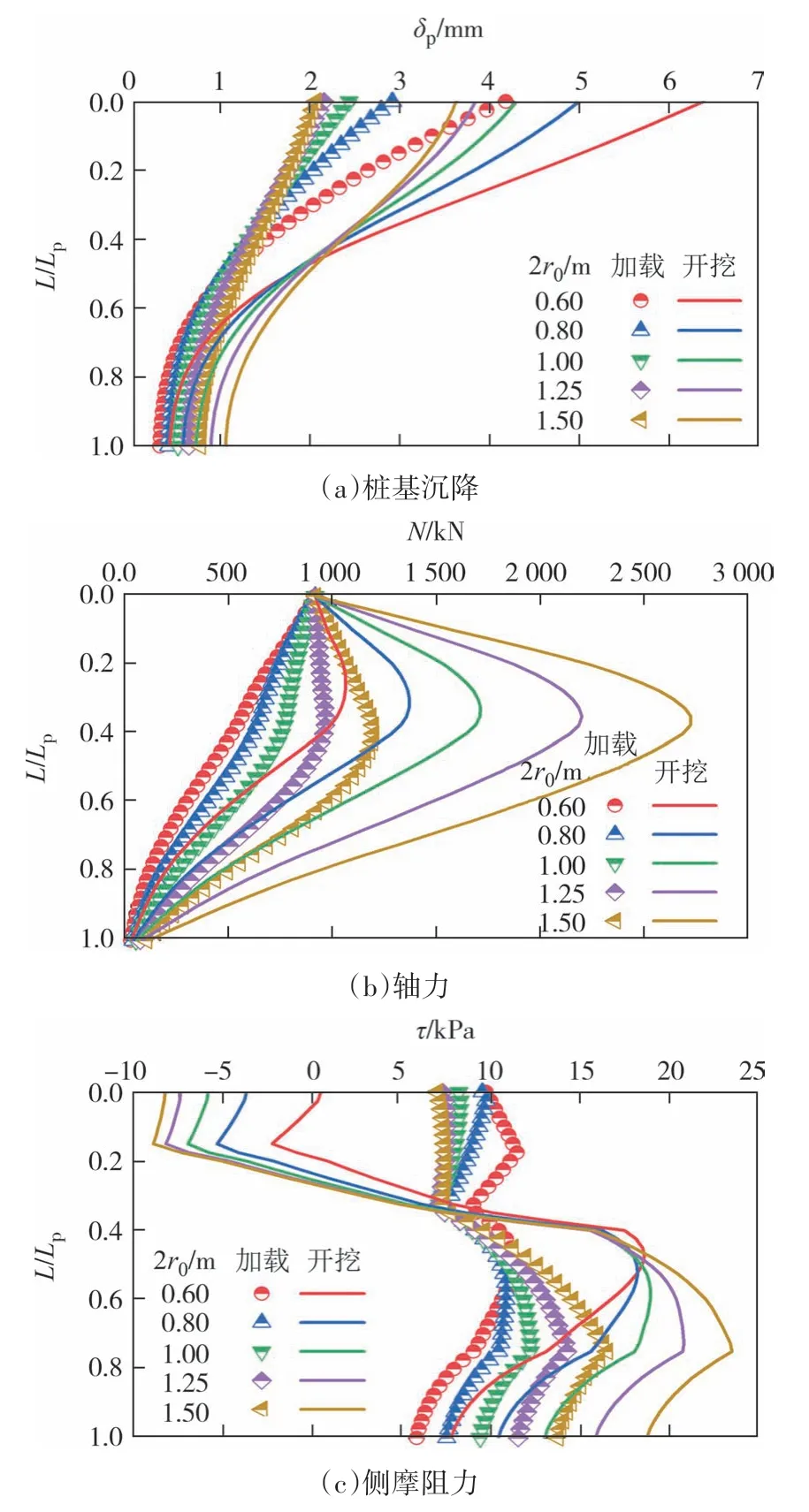
图8 桩径的影响Fig.8 Influence of pile diameter

图9 给出不同长度的桥桩在加载和开挖往返剪切作用下的竖向响应对比.由图9（a）可知，对于桩长40 m的较短桩而言，开挖诱发桩基的整体沉降；长桩则表现出接近端承桩的特性，桩基沉降自上而下逐渐变小，以桩身压缩为主；当桩长大于50 m 时，桩土关系基本处于弹性阶段，因此开挖诱发的桩基沉降并不太大.观察图9（b）（c）可以发现，轴力及轴力最大值所在深度随桩长的增大而增大，且变化速率逐渐减小.即使是短桩，侧摩阻力仍未完全发挥，长桩端部附近的侧摩阻力更是出现拐点；进一步发现所有算例的端摩阻力发挥得较少，说明此时桩基状态相较于极限承载力仍有相当的距离.对于长桩而言，长径比的增加使得桩土刚度减小，从而影响其承载能力与变形能力；综合考虑桩长增加引起的自重变化，同样可以认为，对于桩顶承受荷载不大以及后续受近接工程基坑开挖扰动不大的深厚软弱地层中的桥桩桩基，在以桩顶变形为控制目标时，存在一个合理桩长，盲目增大桩基长度而桩端未能进入坚硬地层，不是一个好的选择.

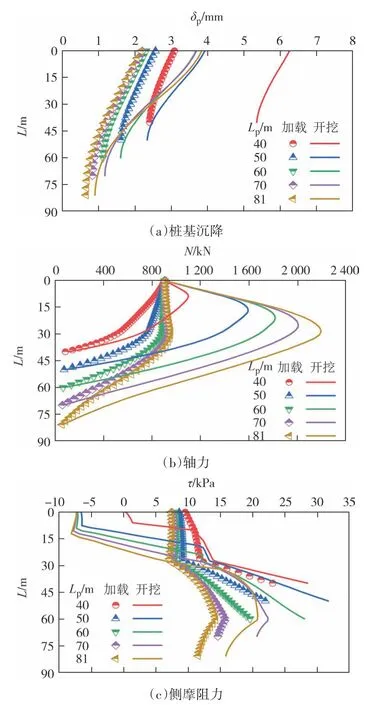
图9 桩长的影响Fig.9 Influence of length of pile

4 结论

1）利用PLAXIS 3D 软件和软土蠕变模型，建立某市政道路下穿市域铁路桥梁基坑工程的三维数值模型，与实测数据的对比验证了模型的合理性.

2）将软土蠕变模型退化为软土模型，考虑桩顶约束条件，对比分析桥梁群桩的时效水平响应，发现土体蠕变对邻近桥梁群桩变形、内力的影响较大，甚至不亚于墙体瞬时变形的影响；桥梁群桩桩身的变形、内力与离开坑壁的距离呈负相关，并表现出群桩的遮帘作用，桩顶的变形、内力则由桩顶约束条件决定.

3）结合两阶段法，将数值计算得到的土体自由场时变沉降作为“外荷载”作用于桩基，利用考虑桩土往返剪切的荷载传递方法，计算桩身自重、桩顶荷载和后续近接工程基坑开挖作用下桩基的竖向力学响应.计算结果表明，对于桩顶承受荷载不大且后续受近接工程基坑开挖扰动不大的深厚软弱地层中的桥桩桩基，在以桩顶变形为控制目标时，存在合理桩径和合理桩长.