人体手臂静止性震颤的负刚度吸振效果研究
2024-03-25刘海平刘庆生韩东航姜宇吴鹤鸣
刘海平 ,刘庆生 ,韩东航 ,姜宇 ,吴鹤鸣
[1.北京科技大学 机械工程学院,北京 100083;2.北京科技大学 顺德创新学院,广东 佛山 528300;3.北京大学 第三医院骨科,北京 100191;4.骨与关节精准医学工程研究中心,北京 100191;5.脊柱疾病研究北京市重点实验室,北京 100191;6.南京医科大学 附属南京医院(南京市第一医院),江苏 南京 210002]
人体手臂静止性震颤在临床上表现为一种非自愿型,按一定节奏做近似正弦式的往复摆动运动[1].其中,帕金森病是最典型的静止性震颤之一.据不完全统计[2],75%的患者在3~7 Hz 频率范围内发生静止性震颤,60%的患者在5~12 Hz频率范围内发生姿势震颤,虽然该症状本身不致命,但会导致患者出现肢体活动障碍,甚至严重影响其生活质量.目前,最有效的治疗方法主要是脑深部电刺激术[3]或神经外科手术,但是,高昂的手术费用给患者及其家庭带来沉重的经济负担.另外,随着可穿戴技术发展,科研人员开发出多种可穿戴式静止性震颤抑制装置[4-7].从振动控制角度,多数可穿戴设备属于主动抑振技术范畴,需要输入能量,成本较高且系统复杂,传感器灵敏度和精确度不够,极大限制了该类设备的推广应用.
综合经济性和震颤抑制效果,被动抑振装置已成为热点研究领域之一,已有方案包括线性吸振器[8-10](Linear Dynamic Vibration Absorber,LDVA)、非线性能量阱[11]、颗粒阻尼器[12]、空气弹簧[13]等.对比发现,被动线性抑振装置有效工作频带宽度有限,而非线性抑振装置则存在稳定性不足的问题.
针对前述缺陷,科研人员提出负刚度吸振器(Dynamic Vibration Absorber with Negative Stiffness,DVA-NS)的概念.在基础理论方面,主要集中于参数优化[14-16]和组合多种力学元件[17-18]探索改善其减振性能的研究;在工程应用方面,已在海洋船舶[19]、轨道交通[20-21]和风力发电[22]等工程领域开展研究.但是,现有研究均将负刚度吸振器与“大地”连接;显然,从实际出发很难实现负刚度“接地”.因此,考虑负刚度吸振器的非接地特征[23],通过优化设计和不同类型吸振器(Dynamic Vibration Absorber,DVA)对比研究,发现非接地负刚度吸振器的减振效果显著优于传统线性吸振器.
综上,本文首次提出采用非接地负刚度吸振器抑制人体手臂静止性震颤.首先,建立含负刚度吸振器的人体手臂耦合动力学模型;然后,推导给出各关节位置的动态响应;进一步利用序列二次规划算法获得负刚度吸振器的最优设计参数,并与传统线性吸振器进行对比,对其振动控制效果展开讨论.本文相关研究成果可为开发面向人体手臂静止性震颤的可穿戴治疗装备奠定理论基础.
1 负刚度吸振器介绍
本文提出的负刚度吸振器结构方案,如图1 所示.由图1 可见,负刚度吸振器主要由装置外壳、惯性质量、滚球、钢丝绳、压盖接头、橡胶、支承质量、竖直导轨等组成.惯性质量通过两个支承弹簧与装置外壳相连;同时,为防止结构运动偏移及不利影响,两侧通过滚球导向并减小接触摩擦.其中,负刚度由预紧后的钢丝绳提供;钢丝绳穿过支承质量,两端与惯性质量连接.支承质量通过压盖接头与底部橡胶相连,并提供正刚度和阻尼.另外,在装置外壳底部安装竖直导轨,实现支承质量在固定平面内滑动,保证支承质量在运动过程中始终垂直于前臂.

图1 负刚度吸振器结构示意图Fig.1 Structural diagram of the DVA-NS
2 理论建模
为了方便研究,本文所建人体手臂理论模型满足如下假设[11,24]:
1)肘部锁定,限制胳膊与前臂之间绕着肘关节的相对运动,即:当前臂与上臂处于一条直线时,限制肘关节发生超伸现象;
2)不考虑肌肉的弹性特征;
3)不考虑胳膊的空间三维运动;
4)手部与前臂等效为一体,不考虑手部与前臂的相对运动.针对人体手臂空间多自由度震颤研究不属于本论文的讨论范围.
基于所建人体手臂模型,本文主要针对负刚度减振方案进行研究,建立“含负刚度吸振器—两自由度人体手臂”耦合动力学模型,如图2 所示.其中,负刚度吸振器对应的理论模型中m3、m4、c3、k3、k4、ka分别对应图1 中的支承质量、惯性质量、竖直橡胶块提供的阻尼、竖直橡胶块提供的刚度、支承弹簧的刚度、钢丝绳提供的负刚度.而且,H、J 分别代表肩关节和肘关节;m1、m2分别为上臂质量、前臂质量;l1、l2、a1、a2、la分别为上臂段和前臂段的长度以及肩关节到上臂质心、肘关节到前臂质心和吸振器安装点到肘关节的距离;k1、k2、ks、c1、c2和cs分别为各部分肌肉刚度和阻尼系数;θ1、θ2、x2和x3分别为上臂关于肩关节和前臂关于肘关节的角位移,以及m3和m4相对于前臂的位移.

图2 含负刚度吸振器的人体手臂模型Fig.2 Model of human arm with DVA-NS
结合所建坐标系,可得负刚度吸振器安装点坐标为:
将安装点处的速度沿垂直于前臂方向(x2方向)分解,最终可得到安装点沿x2方向上的速度表达式:
综上,可以得到安装负刚度动力吸振器的人体手臂耦合动力学模型的动能Ek、势能Ep以及耗散函数D分别为:
式中:第四项、第五项分别是质量块m3和m4的动能.
式中:第四项、第五项和第六项是吸振器上弹簧对应的弹性势能;第七项及之后各项是相应的重力势能.式中:第一项为肩关节处的阻尼做功;第二项为肘关节处的阻尼做功;第三项为双关节处的阻尼做功;第四项为吸振器上阻尼做功.
对于手臂不同关节,其任意位置可以表示为θi=θ0i+θsi(其中,θ表示手臂不同关节位置的角位移,i=1和2 分别表示肩关节和肘关节,θ0i表示初始角位移,代表人体手臂的初始姿态,θsi表示角位移变化量,代表上臂和前臂的旋转角度).假设,人体手臂以小幅角位移运动,故sinθi≈θi、cosθi≈1.因此,为了便于研究,忽略高阶项,将非线性运动方程进行线性化处理.
利用拉格朗日方程,得到人体手臂运动微分方程.
而且,I1和I2分别为上臂和前臂质心的转动惯量;F1和F2分别为作用于肩关节和肘关节的外部激励力矩的幅值,ω表示激励力矩频率,外部激励力矩由手臂震颤时肌肉伸缩产生的力矩与关节处的阻力矩共同构成.
引入参数:λ1=ω/ω1,ν1=p2/p1,ν2=ω3/p1,ν3=ω4/p1.求解式(8),可得肩关节和肘关节振幅X1和X2:
对式(9)进行无量纲化处理,引入静态位移δ1,肩关节振幅放大系数A1和肘关节振幅放大系数A2,可得:
根据文献[10],人体手臂设计参数如表1所示.
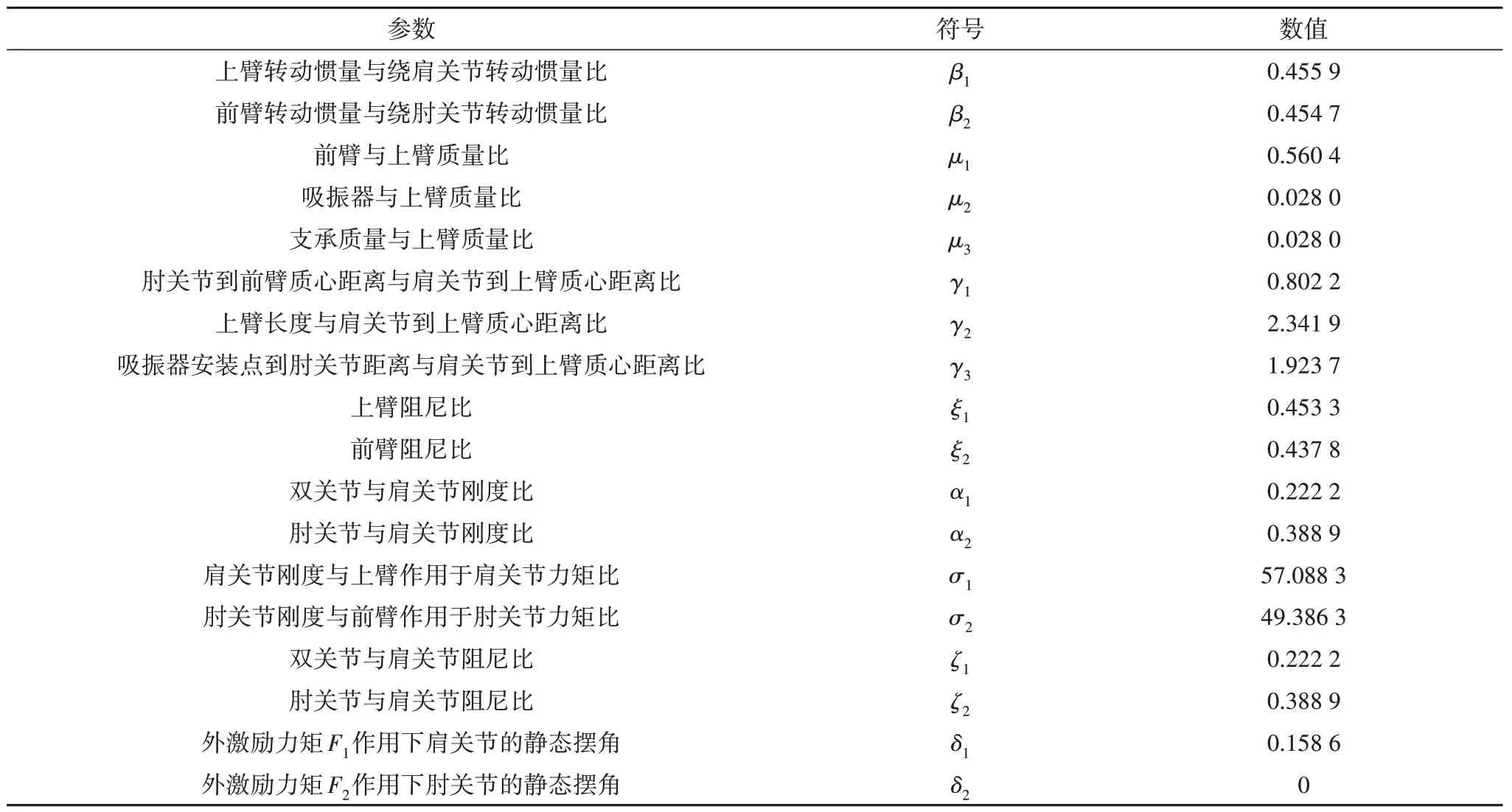
表1 设计参数[10]Tab.1 Designing parameters[10]
3 优化设计
由于传统固定点理论过程复杂,且较难获得解析解,本文选择采用序列二次规划算法,通过求解最大值最小化问题获得最优设计参数,该算法的有效性已经在文献[15]、文献[25]中得到验证.
由于人体手臂两自由度模型中,肩关节和肘关节的幅频曲线存在两个谐振峰,H∞优化的最终目标是等峰降幅,本质上是最大值最小化问题,利用 fminimax 函数编写优化程序.具体优化设计思路:为使肩关节和肘关节振幅放大系数A1和A2的峰值达到最小;选取质量比μ2为0.028,设计变量为负刚度吸振器的刚度比α3和α4取值范围为(-1,0),阻尼比ξ3为(0,1),频率比v2为(0,10).对应负刚度吸振器的优化数学模型定义为:
式中:肩关节和肘关节振幅放大系数A1和A2为由负刚度吸振器刚度比α3、α4,阻尼比ξ3和频率比v2作为变量的目标函数.
利用上述优化方法计算得到负刚度吸振器的最优设计参数如表2 所示.同时,为方便后续与传统线性吸振器进行对比,选取质量比μ2为0.028,线性吸振器设计变量频率比v2的取值为(0,5),阻尼比ξ3为(0,1),利用上述优化算法得到线性吸振器的最优设计参数如表2所示.

表2 吸振器最优设计参数Tab.2 Optimal designing parameters of dynamic vibration absorber
4 计算结果分析
4.1 频响曲线
为了研究负刚度吸振器对人体手臂肩关节和肘关节动态响应的控制效果,与传统线性吸振器最优结果进行对比,计算得到幅频响应曲线,分别如图3和图4 所示.可以看出,人体手臂未安装吸振器时,肩关节和肘关节的频响曲线均呈现两个谐振峰.其中,频率比为0.6附近的谐振峰对应人体静止性震颤的特征频率约为5 Hz,频率比为1.3附近谐振峰对应人体姿势震颤的特征频率约为11 Hz.人体手臂安装负刚度吸振器比传统线性吸振器对应肩关节和肘关节的共振峰显著降低,且有效抑振频带更宽.

图3 幅频响应曲线(肩关节)Fig.3 Amplitude-frequency response curves(shoulder joint)

图4 幅频响应曲线(肘关节)Fig.4 Amplitude-frequency response curves(elbow joint)
此外,对于肩关节而言,安装负刚度吸振器和线性吸振器在全频段内均未放大系统响应.对于肘关节而言,在频率比为0.65~0.85 时,安装负刚度吸振器和线性吸振器均会放大系统响应;在频率比为0.5~0.65 和频率比为1.1~1.6 的范围附近,相比线性吸振器,安装负刚度吸振器抑振效果更好,且有效抑振频带更宽.
4.2 数值验证
为保证上述优化结果的正确性,采用龙格库塔方法求解系统响应的数值解.代入表2 的最优设计参数,分别得到安装不同类型吸振器时肩关节和肘关节的幅频响应曲线,并与解析解曲线进行对比,如图5 和图6 所示.从图中可以看出,安装不同类型吸振器时人体手臂耦合动力学模型的幅频响应曲线解析解和数值解完全吻合,解析解计算结果正确.
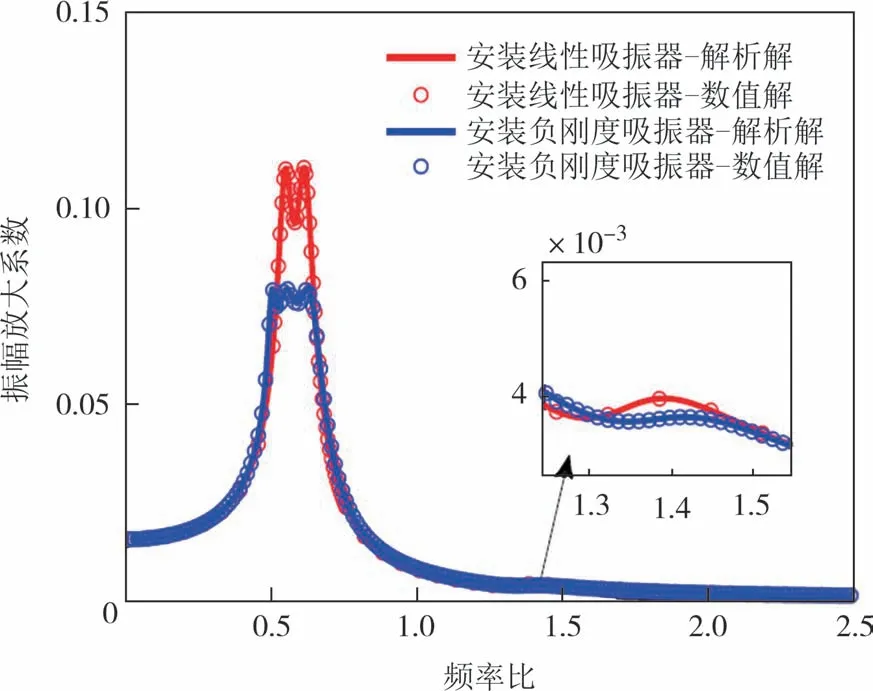
图5 幅频响应曲线解析解与数值解对比(肩关节)Fig.5 Comparison of analytical solution and numerical solution of amplitude-frequency response curves(shoulder joint)
4.3 时域响应
现实中,环境激励多为随机激励,从实际工况考虑,本部分重点研究随机激励条件下安装不同类型吸振器对人体手臂震颤的控制效果.
首先,构建50 s 服从正态分布的随机力矩激励,作用于肩关节处,均值为0,方差为1,力矩幅值为0.5 N·m,如图7所示.
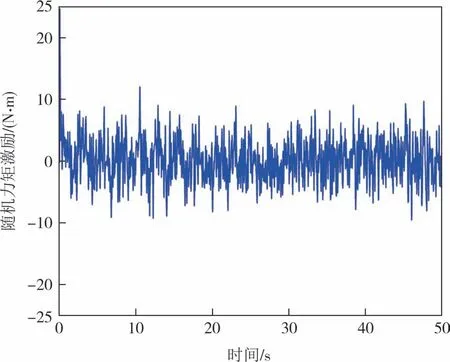
图7 随机力矩激励信号Fig.7 Random torque excitation signal
利用所建理论模型分别计算得到安装吸振器前、后人体手臂的时域动态响应结果,如图8 和图9所示.从图中可以看出,不同类型吸振器均可有效控制人体手臂的动态响应;其中,负刚度吸振器的控制效果优于传统线性吸振器.

图8 安装吸振器前、后肩关节时程角位移曲线Fig.8 Angular displacement curves of shoulder joint with/without absorbers in time domain
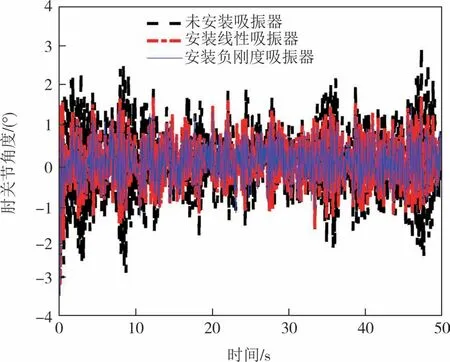
图9 安装吸振器前、后肘关节时程角位移曲线Fig.9 Angular displacement curves of elbow joint with/without absorbers in time domain
为了直观对比不同类型吸振器对人体手臂静止性震颤的控制效果,将人体手臂各关节部位在时间域动态响应的均方根作为评价指标,计算结果如图10 和图11 所示.可见,传统线性吸振器和负刚度吸振器可以分别使肩关节角位移均方根衰减约为36.5%和44.1%;使肘关节角位移均方根衰减约为34.8%和46.5%.显然,负刚度吸振器的振动抑制效果优于传统线性吸振器.

图10 安装吸振器前、后肩关节角位移均方根Fig.10 The mean square root values of angular displacement of shoulder joint with/without absorbers
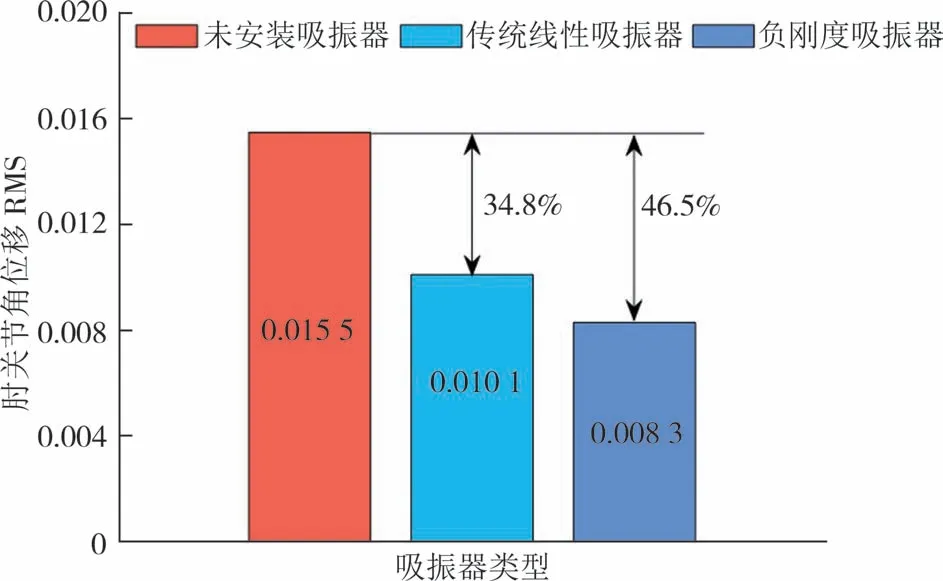
图11 安装吸振器前、后肘关节角位移均方根Fig.11 The mean square root values of angular displacement of elbow joint with/without absorbers
5 结论
针对人体手臂震颤的响应特征,本文提出一种负刚度吸振器并建立耦合动力学模型,分析研究该方案用于抑制人体手臂震颤的可行性.利用所建理论模型,采用序列二次规划算法求得负刚度吸振器的最优设计参数.在此基础上,分别得到正弦激励和随机激励条件下,人体手臂各关节位置的动态响应.根据计算结果可以得到如下结论:
1)受正弦激励,负刚度吸振器对人体手臂不同关节部位的动态响应控制效果显著优于传统线性吸振器.
2)受随机激励,负刚度吸振器对窄带随机激励的控制效果优于传统线性吸振器.
3)以时间域随机振动响应的均方根作为评价指标,负刚度吸振器对人体手臂各关节位置动态响应的衰减率分别为44.1%和46.5%,优于传统线性吸振器的控制效果.
上述研究工作可为后续研制基于负刚度吸振原理的人体手臂静止性震颤可穿戴治疗装备提供参考和理论基础.另外,下一阶段将利用已有人体手臂震颤模拟系统开展负刚度吸振器抑振效果测试及评估.
