考虑风电不确定性的电气综合能源系统混合尺度调控
2024-03-25谭阳红惠玲利杨勃郭潇潇罗琼辉
谭阳红,惠玲利 ,杨勃,郭潇潇,罗琼辉
(湖南大学 电气与信息工程学院,湖南 长沙 410082)
为实现全球能源危机背景下低碳经济和可持续发展目标,可容纳大量分布式储能设备的电气综合能源系统成了学术界研究焦点[1].而物理侧风电的不确定性和多能传输差异往往会导致系统调控分析出现偏差.因此研究其对电气综合能源系统调控的影响具有重要意义.
因包含可再生能源的综合能源系统存在发电随机性、间歇性等不确定性问题[2].部分学者针对风电不确定性采用分布函数[3-4],运用场景生成[5-7]和削减[8]的方法进行处理,另一部分学者则对系统运行不确定性进行优化研究[9].在实际运行过程中,不确定变量的分布函数往往很难精确获得,场景生成的方法比较耗时,有时只能获得其出力的上界和下界.故采用区间数学来处理不确定性优化问题的方法被提出[10].通过建立多能耦合机组不确定的综合能源系统运行性优化模型,采用区间数学表征其不确定性.本文利用分布函数法和区间表征法对风电不确定性进行表示,并给出了处理策略.
目前对综合能源系统时间尺度方面的研究有两类:一类是由预测误差引起的[11-12];另一类是由各类能源传输差异引起的[13].其中预测误差引起的控制时间尺度大多依据新能源和负荷不确定性,从而达到多能互补,保证了设备较高利用率.但上述方法无法满足系统在线调整偏差的要求,故部分学者在此基础上提出了模型预测算法[14-15],有较好的鲁棒性.王成山等[16]建立了日前-日内优化模型,利用MPC(模型预测控制)调节源-荷两侧的资源分配.Ouammi等[17]在日前-日内调控基础上增加了实时调控,构成了多时间尺度优化模型.但上述调控未考虑数据中多能数据传输差异,故栗然等[13]在此基础上考虑了多时间分辨率的动态指标,在日前优化中给定各类能源相同分辨率,在日内滚动优化中根据高分辨率对日前系统出力计划进行修正.但仍未形成统一确定各能源调度周期的方法.考虑到上述研究的不足,本文提出一种基于改进小波融合算法的混合尺度调控,使优化分析过程及最终制定的机组出力计划更加合理.
本文首先分析了风电各时刻出力情况和数据传输过程,提出考虑风电不确定性的电-气互联综合能源系统运行演化过程,对风电的不确定性进行表示,并提出处理策略,完成了调控动态成本计算.其次考虑到不同能源传输特性的差异,对不同能源子层设置了不同调度周期,提出了基于改进小波融合算法的混合尺度调控,即利用改进后的多个小波基的数据融合算法,进行不同小波基的逆变换得到重构信号并做最终融合.最后在改进IEEE30 节点电力网络和20 节点天然气系统构成的电-气互联综合能源系统完成不同尺度下不同调控方法的系统调控结果分析.
1 电-气互联综合能源系统框架
图1 为电-气互联综合能源系统框架.本文建立了含风力发电的可再生能源调度模型,气源输出的天然气通过管道注入储气设备中,天然气系统和电力系统通过燃气轮机组和P2G(可再生能源发电)设备紧密相连,当电负荷需求大于系统总出力时,将储气设备中的天然气通过燃气轮机组进行补充发电,从而满足电力系统中负荷需求.反之,当风电出现大量弃风时,可通过P2G 设备进行风电消纳,将冗余电量转换为天然气储存,使得系统经济运行.

图1 电-气综合能源系统框架Fig.1 Framework for integrated power-gas energy systems
典型天然气系统如图2 所示,其主要由气源、管道、压缩机、传统天然气负荷等构成.其中压缩机是用来弥补管道中降低的气压,确保天然气顺利传输.
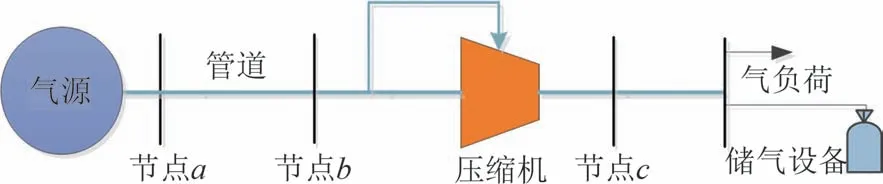
图2 天然气系统结构Fig.2 Natural gas system structure
2 风电不确定性表示及处理策略
考虑到电-气综合能源系统运行过程中存在风电不确定性,另因预测误差近似服从正态分布,在此通过式(1)中的风电误差概率密度分布特性来表示.
上式中φ为预测误差均值,ω为实际出力.在该过程中若产生冗余风电用式(2)表示;若出现缺额风电用式(3)表示.
式中,Pw为风电预测值,ωmax是风电可容纳区间上限值.
为更好突出风电不确定参数对系统的影响,采用优化区间的方法来应对电气综合能源系统中存在的风电不确定性问题.t时刻风电出力区间形式如式(4).
式中,Pw,t表示t时刻的风电出力;表示风电出力下限;表示风电出力上限.
依据图3 区间求解几何描述所示,利用中心极限定理求出风电出力区间数的中心点和区间半径用式(5)~式(6)表示.
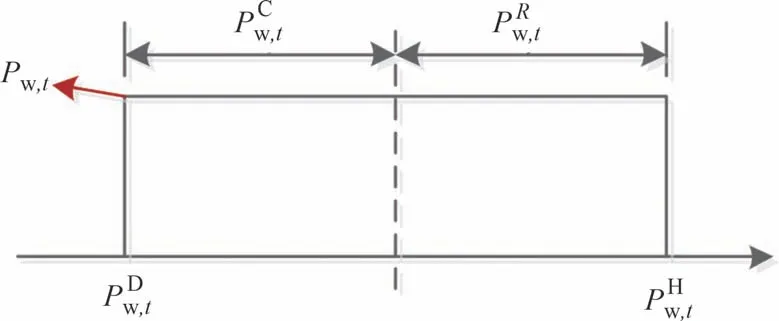
图3 风电出力区间求解几何描述Fig.3 Geometric description of wind power output interval solution
最后,风电不确定水平可定义为式(7).
上式是对风电发生波动概率的表示,其中γ越大,说明风电出力波动性越大,反之越小.
另考虑到可再生能源接入输电网时需要集中开发,规模外送,进行大范围消纳.故针对上述所提不确定性,本文通过快速搜索风电历史数据,采用分时步多阶段模型进行求解,具体调控过程见图4.
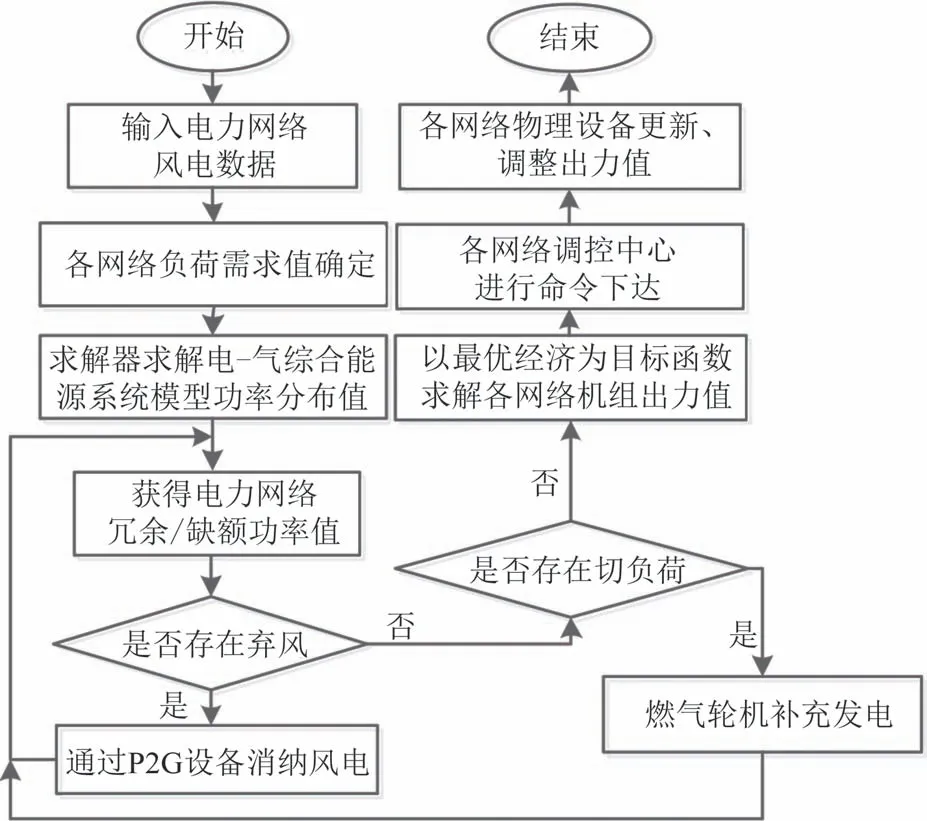
图4 风电不确定性调控Fig.4 Wind power uncertainty regulation
为增大风电利用率及系统对风电的消纳能力,对电-气综合能源系统模型中风电不确定性出力进行处理.如图4 所示,将含风电网络的机组组合出力转换为混合整数规划问题,通过风电预测出力区间及负荷预测数据,制定满足各项约束条件的机组出力计划.即首先获取风电历史数据,考虑负荷侧需求后计算各网络功率情况,在允许合理弃风、切负荷的前提下,通过对风电不确定区间以及负荷电量的适当减缩以避免系统在极端场景下运行,将弃风电量、切负荷电量及机组出力调整进行反馈.该过程中若风电存在冗余,打开P2G 设备完成风电消纳任务,若存在切负荷现象便启动燃气轮机进行补充发电.
3 混合尺度调控
综合能源系统具有结构复杂化、多时间尺度等特点,如电能传输快不易存储,事故损失大;天然气传输较慢,有一定存储规模,事故后有延迟效应;风能分布分散,随机性较大.基于此,本节提出改进小波融合算法的混合尺度调控方法,利用各子调控中心的传感器数据融合,总调控中心指令下达的方式来改善多能传输差异的影响.
3.1 目标函数
以最优成本为目标函数,式(8)、式(9)为系统成本计算.
式中,C、Cm、Cg、CP2G、CM、Ctm、CW、CLoad分别为综合能源系统总运行、燃煤机组发电、气源出力、P2G 设备运行、燃气轮机运行、碳排放、弃风以及负荷投切成本;Ωs、Ωm、Ωg、ΩP2G、ΩM、Ωtm、ΩLoad分别为情景、燃煤机组节点、气源节点、P2G 设备耦合电网节点、燃气轮机耦合电网节点、风电机组节点以及负荷节点集合;T为周期;qs、αi、βi、γi分别为情景发生概率、第i节点燃煤机组发电成本函数系数;PLoad_e、PLoad_g分别为第i节点燃煤机组、燃气轮机、风电最大出力、风电实际出力、电、气负荷投切值;Qsource、QP2G分别为气源出力、P2G 出力;分别为气源价格、P2G 气流量费用、第i个节点燃气轮机运行、弃风以及电、气负荷投切成本;分别为碳排放量、碳排放分配额、燃煤发电机组碳排放系数、单位供电量碳排放系数.
3.2 约束条件
以下是电气综合能源系统调度过程中的约束条件.
1)电力网络约束
式中,PGi、PLj分别为电机、负荷有功功率;分别为电机出力最大、最小有功功率,接入最大、最小负荷有功功率,机组投入工作总功率和接入负荷总功率.
为简化分析,设线路阈值容量为初始潮流值的2.5倍[18].
另考虑到节点功率存在自身波动性,对不同类型节点进行分类判断,式(12)为系统出现断线情况的判据.
Psj、Psi、PGallow、PLallow指实际电负荷节点需求量、实际电机可发总量、电机长期运行允许最大功率、线路长期运行允许最大功率.若式(12)中Δ>0,说明物理系统发生扰动;若Δ≤0,说明物理系统可在所承受功率内正常运行.2)燃气轮机约束
3)P2G约束
4)天然气流量约束
以图2天然气管道ab,气体流向为节点a至节点b.其中天然气流量约束如式(15)~式(16).
式 中,Qab,t是t时刻天 然气管 道b中流通 的流量;sgn(Pa,t,Pb,t)代表流动方向;Pa,t、Pb,t是t时刻节点a、b处的压力值,Cab是常数,由式(17)给出.
式中,T0、p0为标准温度、绝对压力,其值分别为 15.74 ℃、101.01 kPa;Dab、Lab是管道ab直径、长度;G是气体比重;Fab是管道ab摩擦系数;Za、Tab分别是气体平均压缩系数和平均气体温度,其中Za值为0.997 97.
对于含压缩机j的天然气管道bc,其压缩比存在以下约束条件,如式(18).
式中,Rj,max和Rj,min是压缩比限值.
5)综合能源系统功率平衡约束
式(19)~式(20)是系统功率平衡约束和风电约束.
3.3 混合尺度调控方法介绍
针对多能数据传输差异的问题,提出基于改进小波融合算法的混合尺度调控方法,其主要思想是提出一种新的基于多个小波基的数据融合算法,先对电力网络中的传感器信号数据进行多个不同小波基的多尺度分解,然后对天然气系统信号数据使用相同小波基分解的信号在多尺度上实施加权数据融合,之后进行不同小波基的逆变换,得到重构信号,最后将基于不同小波基的重构信号做最终融合.具体流程见图5.

图5 混合尺度调控流程Fig.5 Hybrid-scale regulation process
依据图5,下面以3 只传感器为例对多小波基数据融合过程进行介绍,对于多小波基多传感器的融合方法可由此类推,基本步骤如下:
1)选择3 个具有不同性质的小波基,分别对含有噪声的传感器原始数据进行多尺度小波分解,将问题放到多尺度空间中处理.
小波基函数及尺度变换函数存在如下关系.
式中,hk和gk为正交共轭滤波器系数,且分解算法如式(22).
2)基于各个传感器的观测信息,在不同尺度上得到目标信号分解到该尺度上的小波系数和最粗尺度上的尺度系数的估计值.
3)对各分解层分别进行多传感器的融合处理时,各分解层上的不同频率分量,即每个尺度上的目标信号的小波系数和最粗尺度上的尺度系数,可采用相同或不同的融合规则进行融合处理,得到融合后各层小波系数.式(23)、式(24)为气网络和电网络数据分解,式(25)是融合过程.
若将f(t) ∈V0划分为细尺度和粗尺度,再将f(t)投影到粗尺度空间,就可得到不同尺度下的粗尺度信号,且其表达式如下.
式中,cj,k为小波粗尺度展开系数.
同理,若将f(t)投影至细尺度空间,就可得到不同尺度下的细尺度信号.
式中,dj,k为小波细尺度展开系数.
若将f(t) ∈L2(R)按式(24)展开,其中j为任意设定尺度,则
式(25)为小波变换重构.
以式(23)~式(25)为网络数据分解融合依据,采用多小波基完成数据融合,具体过程见图6.
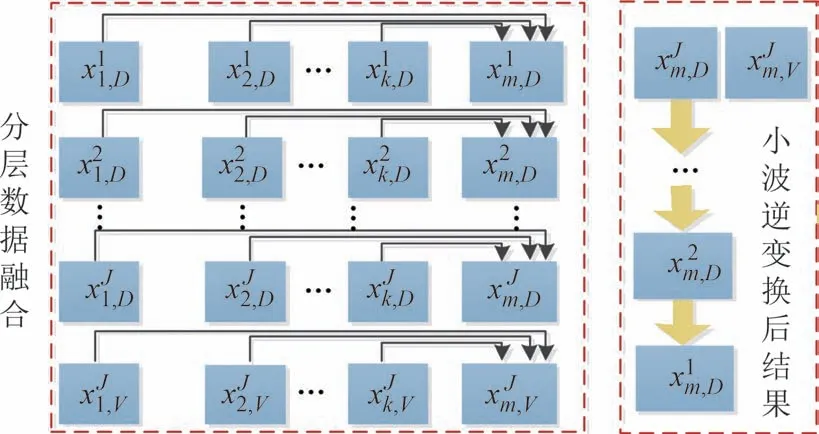
图6 小波混合尺度数据分解及融合Fig.6 Wavelet mixed scale data decomposition and fusion
4)考虑各传感器实际数据值,利用Allan 方差作为权值进行加权融合,融合规则见图7.
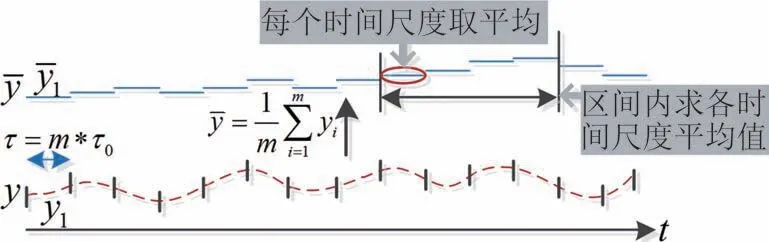
图7 基于Allan方差的数据融合规则Fig.7 Allan′s variance-based data fusion rules
式(26)是和时间尺度相关的方差表达式.
式中,τ为时间尺度;M为时间尺度下的分块数量;y为数据集合;是数据平均值集合.
5)对各层上融合后的小波系数进行小波逆变换,在最细尺度上所得到的重构数据,为基于不同小波基的多尺度多传感器融合结果.
6)将5)中所得融合结果进行加权平均处理,得到融合后的最终目标信号数据.
上述加权平均过程指的是获取电、气网络数据逆变换后对得到的数据进行加权平均融合,得到最终融合信号,考虑到小波系数加权均值的权重一般是满足[-1,1]的二值伪随机序列,所以此处利用各级小波系数绝对值变化量的算数平均值来设置权重.
4 算例分析
以改进IEEE30 节点系统与天然气20 节点系统为例,电力数据见Matpower文件数据,其他网络参数见文献[19],图8 为调度测试系统仿真图,图中传感器组用于接收来自物理网络所采集的数据,主要任务是数据预处理等.
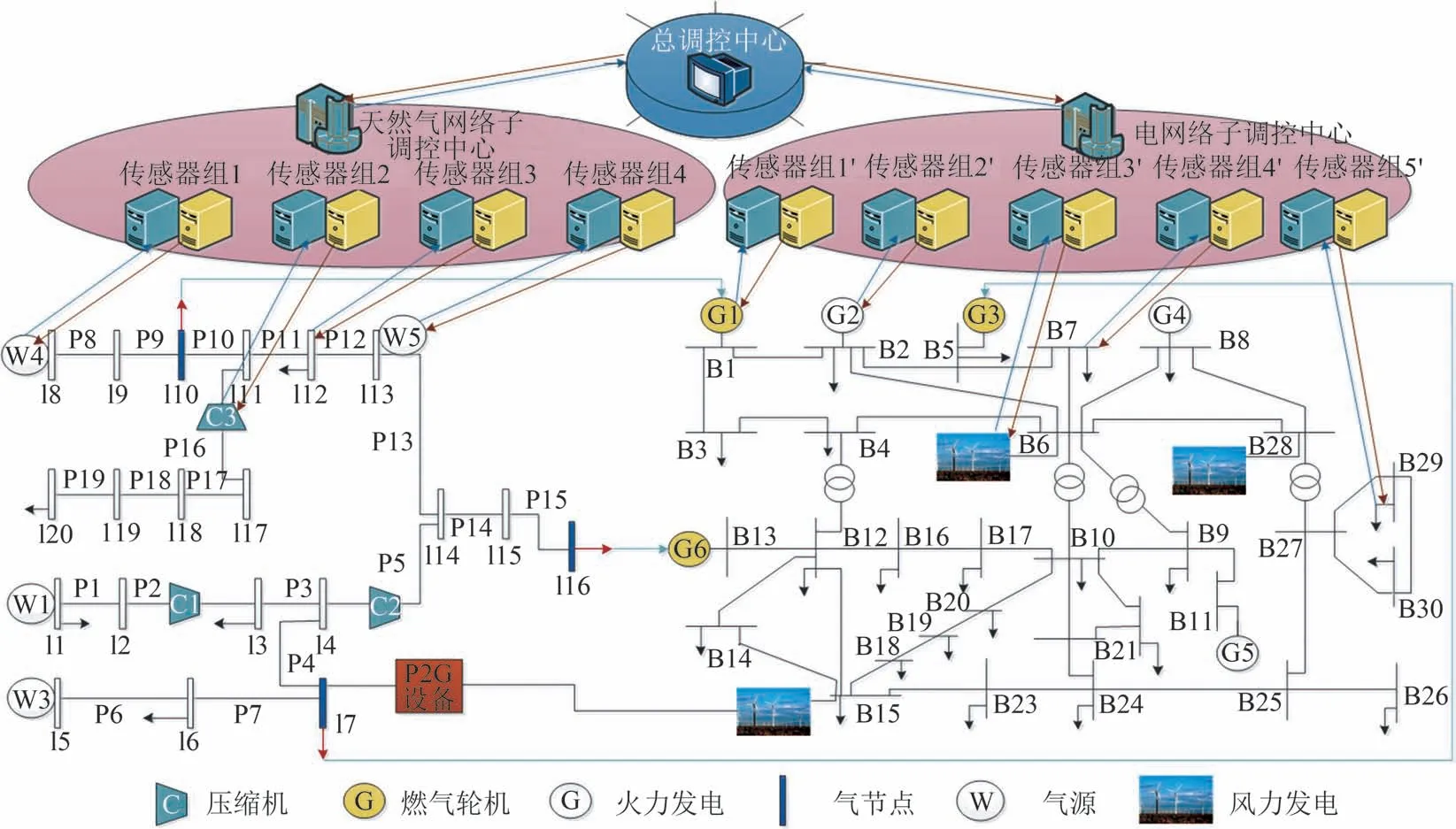
图8 电-气互联综合能源系统混合尺度仿真图Fig.8 Hybrid-scale simulation of integrated power and gas energy systems
4.1 混合尺度系统调控结果分析
电-气互联综合能源系统中各网络多传感器数据分解及融合过程结果图见图9(a)~图9(d),以图9(a)~图9(c)为例,其为基于改进小波融合算法的电力侧、天然气侧和负荷侧传感器数据分解后所得到的波形.依据其波形可明显看出电力侧、天然气侧、负荷侧需求数据的调度周期间隔相差较大,气网在同周期内的数据采集传输速度较慢.在混合调控作用下,电、气网络和负荷侧需求量数据经过数据融合后的信号数据与原始信号数据在同周期内的传输速度差距缩小,更便于总调控中心进行调控指令的下达.
图10 是利用改进小波融合算法后,总调控中心所接收的数据融合值及对系统的调控指令.
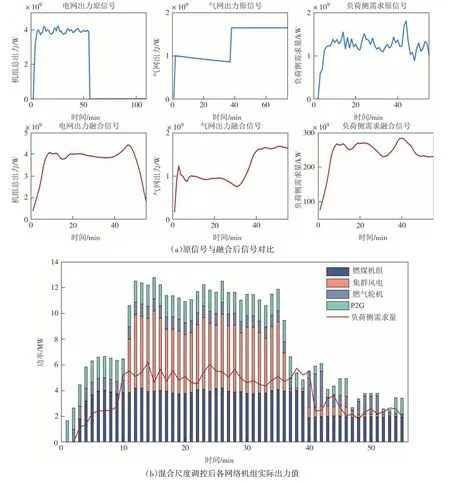
图10 混合尺度下数据融合值及机组出力Fig.10 Data fusion and unit output at mixed scale
图10(a)为原信号与融合后信号对比图,其中原信号是子调控中心收到的信号数据,融合信号是经过改进小波融合算法后总调控中心收到的信号数据,可明显看出对同周期内的系统调度传输速度有所改善,传输差异性减小.图10(b)是混合尺度调控后系统各网络机组实际出力值.其在天然气调度阶段,根据气负荷预测误差和风电出力预测误差对P2G 机组以及储气罐进行出力调整;在电能调度阶段,主要是根据电负荷的预测误差对燃气轮机组和燃煤机组进行出力调整.根据调控结果可明显看出各子系统很好的执行了调控指令,在10~38 min时段中系统对冗余风电处理效果很好,减小了弃风成本,更经济环保.
4.2 不同尺度下不同方法调控结果对比
下面基于DMPC(分布式模型预测控制)滚动优化调控方法[20]和本文所提混合尺度调控方法完成系统调控,并对调控结果进行对比分析.
1)电力侧网络调控对比分析
图11(a)~图11(b)分别为混合尺度和基于DMPC 调控方法下,对负荷侧需求量波动和风电出力调控结果进行对比分析.
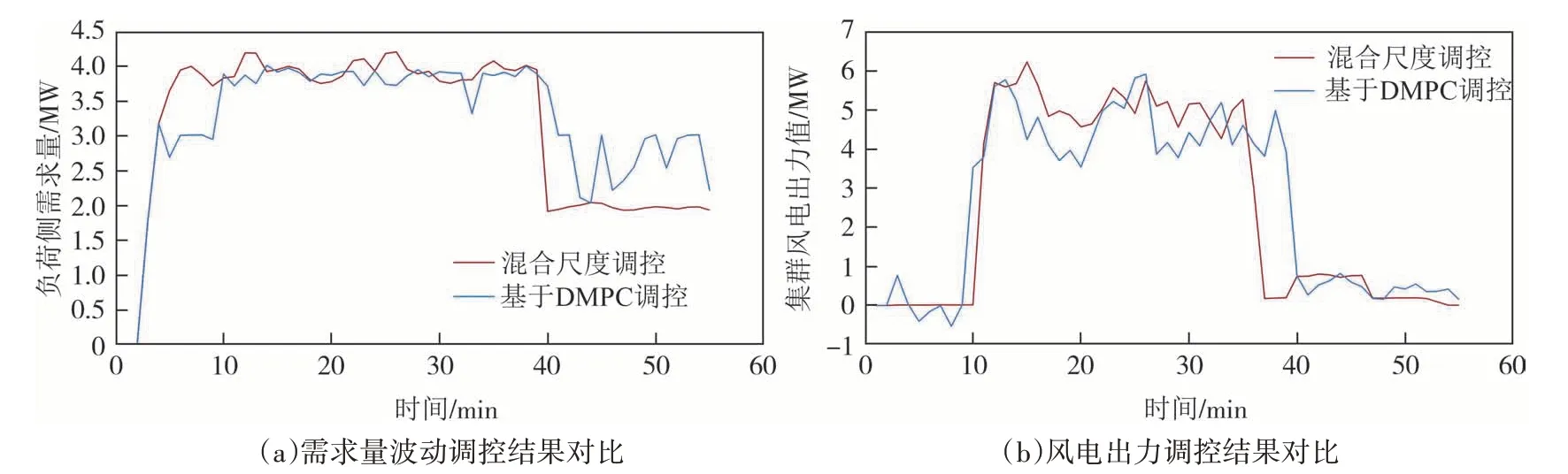
图11 电力侧调控对比Fig.11 Comparison of power-side regulation
图11(a)~图11(b)中两种调控方法下负荷侧需求量和风电出力变化趋势一致,但利用本文所提方法进行混合尺度调控后,负荷侧需求量和风电出力变化相对更加平滑.这是由于混合尺度调控方法已经将各网络的传感器传输数据进行分解融合,总调控中心所得调控数据的调控周期也是经过融合计算的,即电、气网络子调控中心将数据处理后上传至总调控中心,会使得总调控中心所得数据更加精准,而基于DMPC 的调控过程需要协同日前、日内、实时调控,遵循前两个阶段处理计划的前提下满足电负荷需求,当负荷侧需求波动较大时,会导致系统出力波动变大.
2)天然气侧网络调控对比分析
两种调控方法下燃气轮机、P2G 设备的调控结果对比图见图12(a)~图12(b).
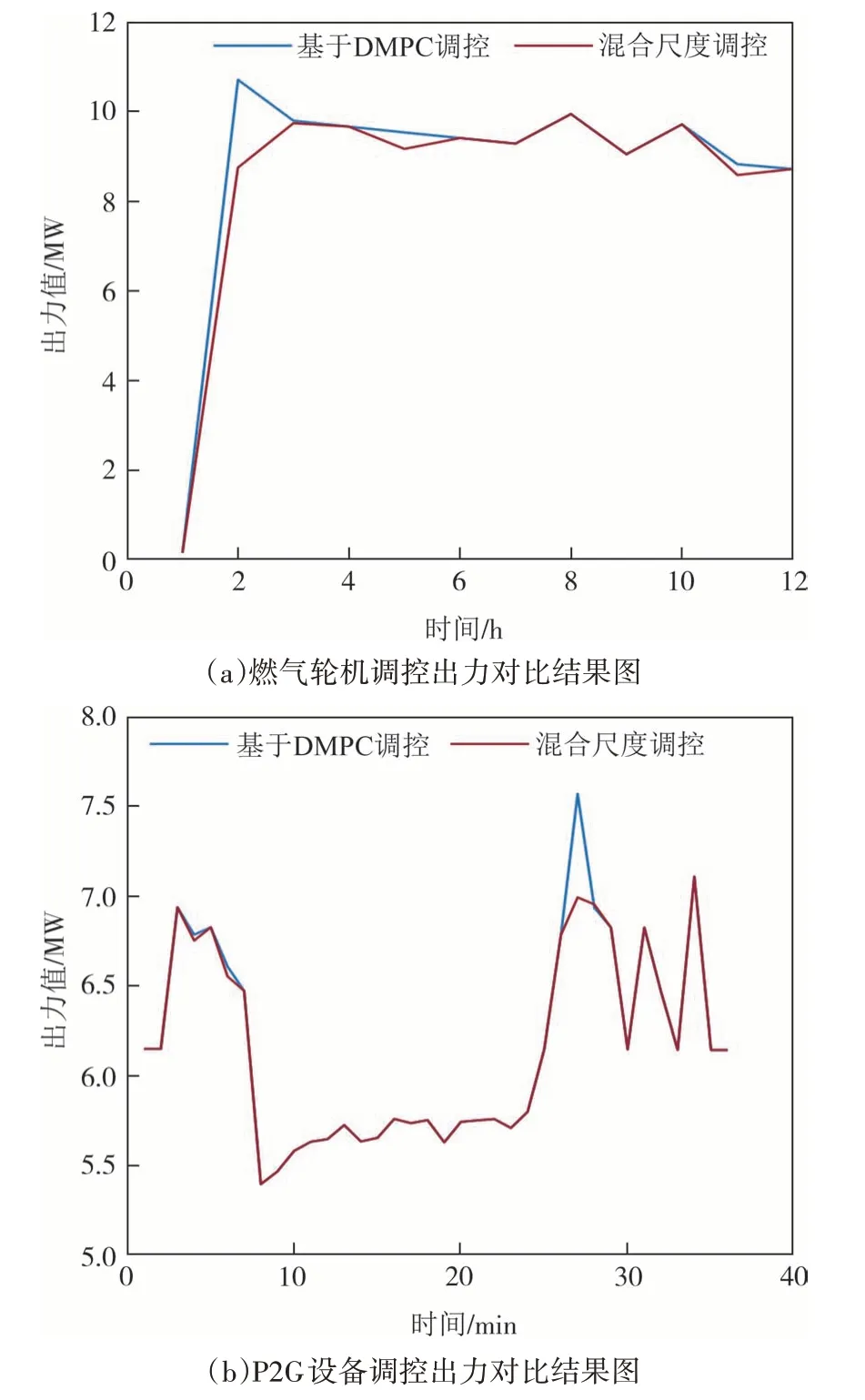
图12 天然气网络各类设备调控对比结果图Fig.12 Comparison of the results of the regulation of various types of equipment in the natural gas network
由图12(a)~图12(b)可知基于DMPC 滚动优化调控与混合尺度调控两种调控方式下的燃气轮机机组、P2G 设备的出力变化趋势基本一致,但混合尺度调控下燃气轮机组和P2G 设备的出力变化在负荷侧功率波动较大的地方对系统功率的跟踪性能更好.图12(a)中基于DMPC 进行调控时波形偶尔会出现尖峰点,这是因为DMPC 滚动优化的内核是将不同尺度逐层迭代,从而达到调控目的,但若系统负荷侧出现波动较大时会导致电、气各自的子调控中心追踪调控,总调控中心指令来不及变更,导致调控过程出现尖峰点.而本文所提经过改进小波融合算法下的混合尺度调控是将子调控中心的数据进行融合后实时传送至总调控中心,一旦出现负荷突变,总调控中心可直接对其进行调控,不存在各能源之间的传输差异,间接提高了系统经济稳定运行能力.
3)系统总运行成本对比分析
如图13 所示,电-气互联综合能源系统在本文所提调控方法下的动态运行成本曲线一直略低于基于DMPC 滚动优化调控后的动态运行总成本曲线,这是因为上述基于DMPC 调控的系统各类设备出力值均略高于混合尺度下的调控结果,故其动态成本值就会略高.如刚开始调控时负荷侧需求突然增大,燃煤机组来不及响应,燃气轮机出力突然增大,导致系统成本值增大.在20~32 min 时段内,风电出力突然增大,启动P2G 设备进行风电消纳,此时存在切负荷成本和弃风成本,故动态成本调控值增大.
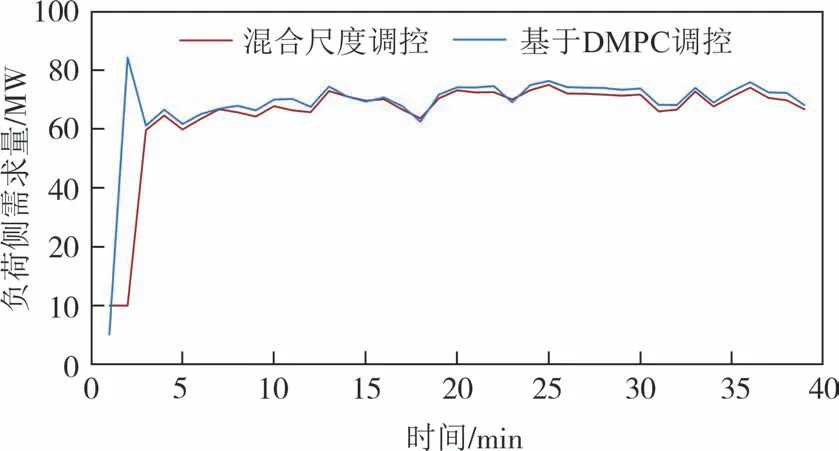
图13 总运行成本对比Fig.13 Total operating cost comparison
5 结论
为了改善由于风电不确定性和网络传输差异引起的系统调控偏差的影响,本文考虑了风电不确定性后,提出基于改进小波融合算法的电-气综合能源系统的混合尺度调控方法.
结果表明,本文所提风电不确定性处理策略能够较好地应对系统风电出力的随机性,对冗余风电消纳能力强;同时基于改进后的小波融合算法在混合尺度系统调控过程中有较好的适应性和鲁棒性;与DMPC 滚动优化调控方法对比,该文所提调控方法在系统经济性和稳定性方面均具有较好的表现.
本文研究重点在于电-气互联综合能源系统中物理侧网络的不确定性因素.然而,随着能源互联网的快速发展,信息侧交互的风险也逐渐增加.因此,信息侧交互不确定性风险将是下一步研究重点.
