一种适用于混合双极直流输电的纵联方向保护方法

高淑萍 ，李元泽 †，宋国兵 ，左俊杰 ，吕宇星 ，沈渠旺

（1.西安科技大学 电气与控制工程学院，陕西 西安 710600；2.西安交通大学 电气工程学院，陕西 西安 710049）

现如今，输电网络正快速发展，在我国，各种资源如煤炭、水能等主要集中在西部地区，而东部地区又是用电负荷的主要集中地区，这种分布的不均衡性使得“西电东送”的政策应运而生［1］.在这种长距离输送情况下，高压直流输电传输容量大，传输损耗小，便成为了研究的热点［2］.传统高压直流输电主要是基于电网换相换流器高压直流输电（Line Commutated Converter Based High Voltage Direct Current-Transmission，LCC-HVDC），虽然这种直流技术建设成本低，但容易出现换相失败的问题.为应对这种问题，便诞生了一种基于模块化多电平换流器型高压直流输电（Modular Multilevel Converter Based High-Voltage Direct-Current Transmission，MMC-HVDC）.这种直流输电功率控制灵活，不存在换相失败的问题［3-4］.同时，为降低成本，减小占地面积，并且综合LCC-HVDC 与MMC-HVDC 的优势，便兴起了混合直流输电系统.但在目前世界上的混合直流输电系统实际工程中，除了广泛应用的混合双端和混合多端直流输电系统，仅在挪威和丹麦之间存在一条混合四极直流输电系统，目前尚没有混合双极直流输电系统实际工程，针对混合双极直流输电系统的研究较少，技术还不是很成熟［5］.相比于混合四极直流输电系统，混合双极直流输电系统成本较低，占地面积小，经济性好.因此，寻找一种合适的混合双极直流输电保护方法来保障输电系统的安全平稳运行是很有必要的.

输电线路通常是输电系统故障的主要区域，故障发生后，需要快速识别故障并使保护快速准确动作［6-9］.目前，高压直流输电的主流保护方法有行波保护、差动保护、低电压保护等，这些保护方法各有优缺点，现有保护一般以行波保护作为主保护，低电压保护和差动保护由于动作时间较慢，一般作为后备保护［10-13］.

Gemmell 等［12］在分布参数模型基础上，以共模补偿电流作为故障识别依据，以差模补偿电流作为故障选极依据，提出了适用于高压直流输电线路的模态电流差动保护算法，但存在通信延迟问题.韩昆仑等［14］根据线路边界元件对特征谐波具有滤波特性，会导致保护安装处的暂态电流特征频带信号在直流线路区内和区外故障时存在着显著的差异性这一特点，提出一种基于Shannon熵的直流线路单端量保护方法，但其对特征频带信号提取要求较高.樊艳芳等［15］基于直流输电线路在区内外故障时，暂态电压在指定高频带Hilbert瞬时能量的幅值以及波形形状存在明显差异，利用标准差综合描述高频带Hilbert能量幅值信息和波形信息，构造直流输电线路故障识别判据，但其对采样装置的要求较高.高淑萍等［16］根据高压直流输电线路边界元件两侧的电压能量不同，将故障时测量点采集的电压故障分量进行变分模态分解（VMD），并计算能量熵，提出了一种基于VMD 能量熵的混合双端直流输电线路纵联保护方法，但其算法较为复杂，实现较困难.高淑萍等［17］根据输电线路发生故障时电压和电流的变化差异，将故障线路单端电流、电压故障分量进行数据标准化处理，利用两者余弦相似度的差异，提出了一种线路保护原理，但其未考虑故障距离对保护的影响.高淑萍等［18］根据混合双极高压直流输电线路边界元件两侧的信号高低频能量存在的差异，构造了有功率故障分量的暂态能量比值的保护方法，但其未考虑故障距离以及噪声对保护的影响.张颖等［19］利用区内故障时线路两侧均有反向行波幅值大于正向行波幅值的特点，构成纵联行波方向保护，但其耐过渡电阻能力较弱.张大海等［20］利用不同故障位置线模电压衰减特性不一致的特性构造未失真因子，进而根据线路两侧线模电压的未失真因子比值特性识别区内、外故障，提出一种基于未失真因子的纵联保护方案，但其需要加装GPS 同步装置，对通信的要求较高.

本文在分析直流输电系统中行波传播特性的基础上，结合平波电抗器和直流滤波器作为边界，根据区内、外故障时前行波与反行波的高频能量差异，提出基于前行波与反行波高频能量差异的纵联方向保护原理.在PSCAD/EMTDC 中对各种类型故障数据进行采集，然后在MATLAB 中对所采集故障数据进行处理，对保护原理进行仿真验证.大量仿真结果表明，此保护原理不受故障类型以及故障发生距离影响，且具有较强的耐过渡电阻及抗噪声能力.

1 LCC-MMC 混合双极直流输电系统结构分析

图1为一个±500 kV 的LCC-MMC 混合双极直流输电系统结构框图.该系统的正极采用LCC 型换流器，负极采用MMC型换流器.

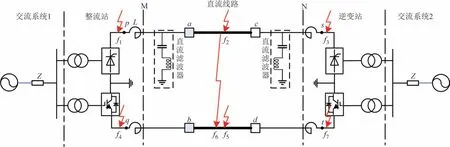
图1 LCC-MMC混合双极直流输电系统结构框图Fig.1 Structure block diagram of LCC-MMC hybrid bipolar DC transmission system

图1 中L代表平波电抗器，平波电抗器作为边界，将直流输电系统分为区内部分（直流输电线路）和区外部分（直流输电线路以外的部分）.a、b、c、d分别为区内线路保护测量安装处.f1～f7分别为不同的故障.其中f1、f3、f4、f7为区外故障，f2、f5为区内单极故障，f6为区内双极故障.输电系统各部分具体参数如表1所示.

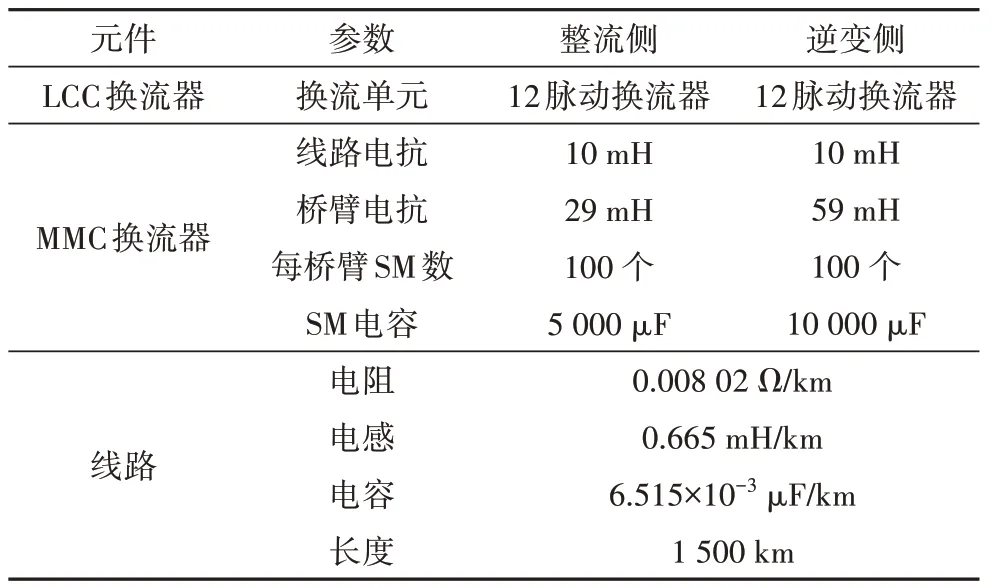
表1 LCC-MMC混合双极直流输电系统各部分参数Tab.1 Parameters of LCC-MMC hybrid bipolar DC transmission system

2 行波传输故障特征及算法

2.1 行波传输过程分析

行波保护原理就是通过故障时故障点产生的行波来检测故障.当故障在线路上发生时，故障点处将产生行波，该行波会以故障点为中心向线路两侧传播，并在阻抗不连续点发生折射与反射［21］.

电压前行波和反行波以及电流前行波和反行波分别为［22］

故障发生后，故障点将产生故障行波，该行波会以故障点为中心，沿着线路向两侧传输，随后在行波到达阻抗不连续点（如故障点或电容电感处）时，发生行波折射和反射现象.

行波传输反射系数和折射系数分别为

λi、βi分别为行波传输的反射系数与折射系数，Z1和Z2分别为两条不同线路的阻抗，易知|λi|＜1，|βi|＞0.

2.2 前、反行波高频能量差分析

图2～图3 分别表示直流输电系统在正方向故障和反方向故障（以整流侧反方向故障为例）下的行波传播过程.M、N分别为整流站、逆变站.L1和L2为平波电抗器，a、c分别为线路首末端的保护测量安装处，设正方向为母线指向线路.

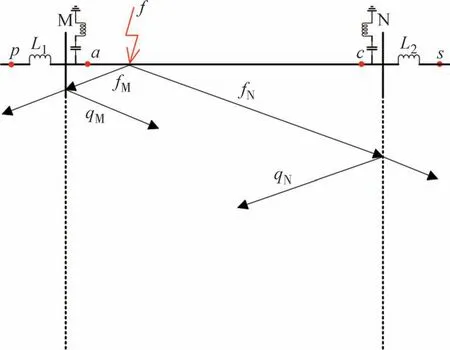
图2 直流输电系统正方向故障时行波传播过程Fig.2 Traveling wave propagation process of DC transmission system with forward fault

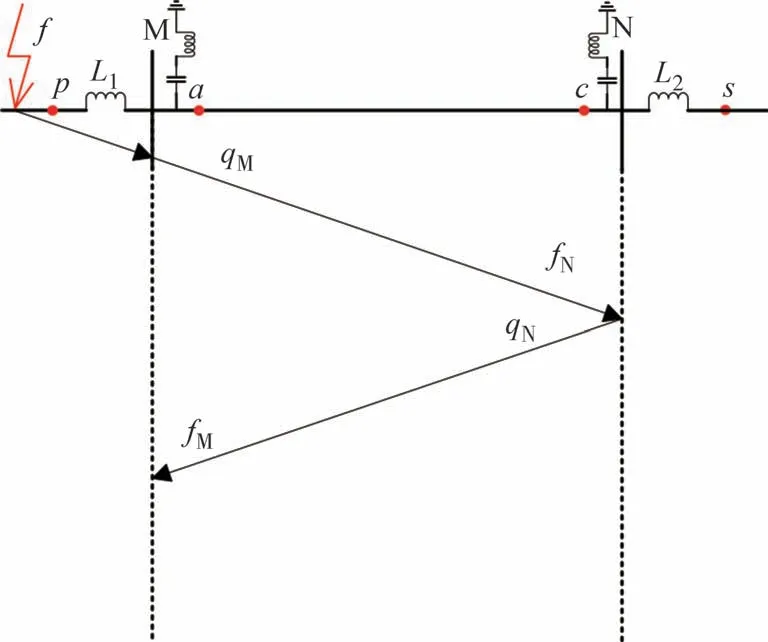
图3 直流输电系统M侧反方向故障时行波传播过程Fig.3 Traveling wave propagation process of M side reverse fault in HVDC transmission system

2.2.1 正方向故障前，前反行波高频能量差分析

由图2 可知，当发生正方向故障时，对于整流侧和逆变侧均为正方向故障.行波由故障点向两侧传输，整流侧和逆变侧保护安装处首先检测到各自的反行波fM和fN.随后该反行波在边界又发生折射和反射，此时两侧保护又检测到各自的前行波qM和qN.此过程中保护安装处检测到反行波fM和fN为初始行波，前行波qM和qN为初始行波经过反射后的反射波.

由式（3）知：反射系数|λi|＜1，且满足前行波q=λif，所以整流侧和逆变侧保护安装处检测到的反行波幅值大于前行波幅值，即|f|＞|q|.

由上述幅值大小关系可推出，在此时间段内，正方向故障后的保护安装处反行波能量大于前行波能量，加上平波电抗器为大电感，其电抗值为ZL=jωL，具有“通低频，阻高频”的特性，大电感L对低频信号显低阻抗，所以低频信号将会通过大电感并传输到区外，而大电感对高频信号显高阻抗，所以大量高频信号会在保护安装处被检测到.同时，在高频反行波能量被检测到之后，部分高频能量会通过直流滤波器被滤除，所以通过边界反射形成前行波之后，保护安装处测量得到的高频反行波能量Ef大于高频前行波能量Eq.

2.2.2 反方向故障前，前反行波高频能量差分析

由图3 可知，以整流侧发生反方向故障为例，行波传输首先到达整流侧，并在平波电抗器处发生折射和反射，此时保护安装处检测到的主要为前行波qM，即初始行波通过边界大电感和直流滤波器后的折射波.此行波继续传输到达逆变侧作为逆变侧反行波fN，并在逆变侧发生折反射，随后逆变侧的反射波作为逆变侧前行波qN继续传播到达整流侧，作为整流侧反行波fM，故在此时间段内整流侧保护安装处检测到的反行波很小，因此整流侧检测到的前行波幅值大于反行波幅值，即|q|＞|f|.

由上述幅值大小关系可推出，在此时间段内，反方向故障的保护安装处前行波能量大于反行波能量，即保护安装处测量得到的高频前行波能量Eq大于高频反行波能量Ef.

此时，对于逆变侧为正方向故障，由2.2.1 节同理分析可得，此时逆变侧高频反行波能量Ef大于高频前行波能量Eq.

综上所述，即当Eq＜Ef时，为正方向故障；当Eq＞Ef时，为反方向故障.

2.3 小波包变换算法

小波变换通过一系列的伸缩变换和平移等运算，能够有效地将信号信息提取出来.但小波分析却也存在一些缺点，其分辨率较高的频段往往在低频段，而在高频段往往分辨率很低，信号无法被有效地提取出来.为克服这一缺点，本文采用小波包变换来获取高频能量信号，小波包变换相对于小波变换来说，其处理非平稳信号的能力要更好，获取的故障特征也更为明显［23］.

定义小波函数为

式中：a为尺度参数，b为位置参数.

小波包分解公式为

式中：j为尺度，m为频带，n为该点的时域位置.

定义某尺度下的变换系数沿时间轴的积分为该尺度下的能量，则第i层第（i，j）个节点能量为：

式中：Ei，j为小波包变换后的第（i，j）个节点的能量值，Wj，k为小波包系数，N为采样点数.

本文采用的仿真模型为LCC-MMC 混合双极直流输电模型，采样频率为10 kHz，采样周期为100 µs.由实际工程经验可知，当采样的频率到达2 kHz 以上时即可有效提取故障信息，所选取的10 kHz 采样频率满足要求.选取分解层数为3，共分解出23=8 个频段.由采样定律可得，采样信号的最高频率为5 kHz，将其分解为8 个频段后各节点频段值分布如表2所示.

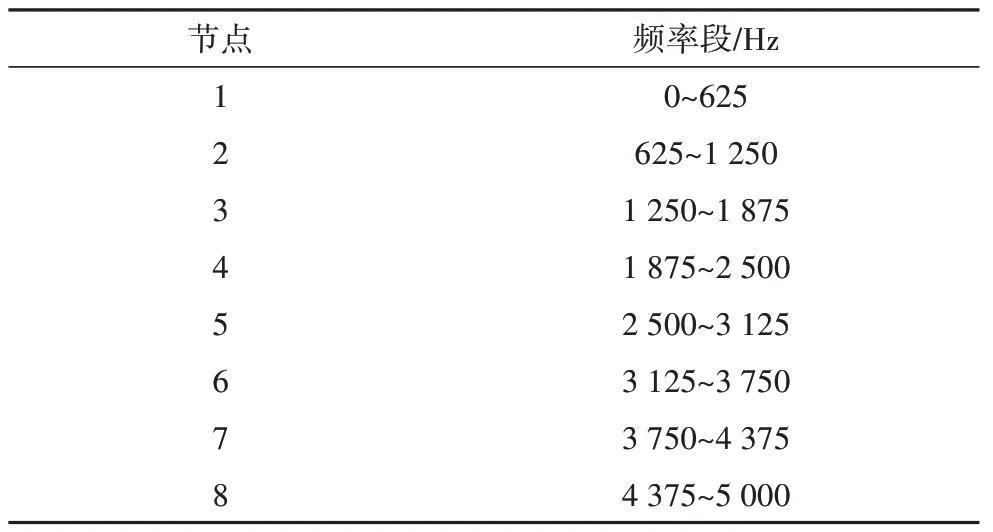
表2 小波包变换第3层分解后各节点频段Tab.2 Frequency band of each node after decomposition of the third layer of wavelet packet transform

3 基于前反行波能量差异的纵联方向保护原理

3.1 保护启动判据

根据故障后差分电流行波的差分和可构造保护启动判据为

其中di（n）和d（in+1）分别表示采样点编号n和n+1的差分电流行波.M为累计次数（经验值为3），Δset为基于保护标准的门槛值.保护启动判据门槛值设定一般需要保证在最不灵敏情况下的故障时保护也可以可靠启动，此处设定为2 A.当式（7）中的条件满足时，保护被激活.

3.2 纵联行波方向保护方案

由2.2 节分析可得，当发生区内故障时，整流侧与逆变侧保护安装处均检测到高频反行波能量大于高频前行波能量.

当发生区外故障时，近故障端检测到的高频前行波能量大于高频反行波能量，远故障端检测到的高频反行波能量大于高频前行波能量.

对于此混合双极输电线路，采用相模变换将耦合的两极输电线路解耦成相互独立的系统.相模变换矩阵为

由式（9）和式（10）可知，经过相模变换后，1模分量为正极和负极的电气量相减得到，保留了两电气量中相反的成分，0模分量为正极和负极的电气量相加得到的，保留了两电气量中相同的成分.由于0 模分量仅能反映出线路的单极故障，不能反应出双极故障，而1 模分量既可以反应出单极故障也可以反应出双极故障，所以本文选取1 模分量来构成保护判据.

则1模电压前行波和1模电流前行波分别为

其中，uPq为正极电压前行波，uNq为负极电压前行波，iPq为正极电流前行波，iNq为负极电流前行波.

1模电压反行波和1模电流反行波分别为

其中，uPf为正极电压反行波，uNf为负极电压反行波，iPf为正极电流反行波，iNf为负极电流反行波.

由此可构成纵联方向保护判据：当整流侧和逆变侧保护安装处均检测为1模高频反行波能量E1f大于1模高频前行波能量E1q时，则判断为区内故障，保护动作；当其中一侧检测到1 模高频反行波能量E1f大于1 模高频前行波能量E1q，而另一侧检测到1 模高频前行波能量E1q大于1 模高频反行波能量E1f时，则判断为区外故障，保护不动作.

3.3 故障极识别算法

当发生区内双极故障时，正极与负极都发生明显波动，其正极高频前行波能量EPq与负极高频前行波能量ENq值相当，正极高频反行波能量EPf与负极高频反行波能量ENf值相当；当发生区内正极故障时，其正极高频前行波能量EPq与正极高频反行波能量EPf均分别大于负极高频前行波能量ENq与负极高频反行波能量ENf值；当发生区内负极故障时，其正极高频前行波能量EPq与正极高频反行波能量EPf均分别小于负极高频前行波能量ENq与负极高频反行波能量ENf值.因此，可得到故障单双极识别为

选极判据的门槛值设定一般需要考虑故障距离以及所设过渡电阻最大情况下的影响，并留有一定的裕度.考虑此因素，本判据k的门槛值取1.8和0.7，则故障极识别算法为

3.4 保护流程图

图4 给出了基于前反行波高频能量差异的纵联方向保护流程框图.

4 仿真验证

通过PSCAD/EMTDC 构建一个±500 kV 的LCCMMC 混合双极直流输电系统，如图1所示.此系统采用频域相关模型，输电线路采用架空线，线路长度为1 500 km，采样频率设置为10 kHz，仿真步长为10 µs，故障时间设置为1 s时故障，采样数据窗设置为3 ms.

4.1 区内、外故障前反行波幅值仿真结果分析

图5 给出了区内故障时整流侧与逆变侧的电流前行波和电流反行波的波形图.

图5 区内故障时电流行波波形图Fig.5 Waveform diagram of current traveling wave when an internal faults occurs

由图5 可知，在3 ms 的数据窗时间内，整流侧与逆变侧电流反行波幅值均大于电流前行波幅值.

图6 给出了整流侧区外故障时整流侧与逆变侧的电流前行波和电流反行波的波形图.

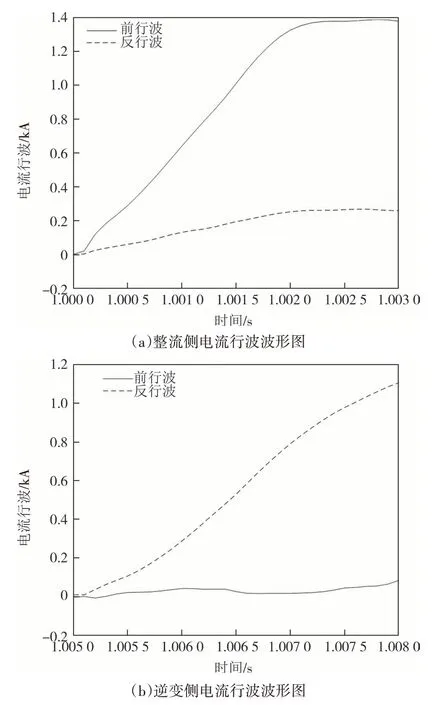
图6 整流侧区外故障时电流行波波形图Fig.6 Waveform diagram of current traveling wave during an external faults occurs on the rectification side

由图6 可知，在3 ms 的数据窗时间内，整流侧（近故障端）检测到的电流前行波幅值大于电流反行波幅值，逆变侧（远故障端）检测到的电流反行波幅值大于电流前行波幅值.

图7 给出了逆变侧区外故障时整流侧与逆变侧的电流前行波和电流反行波的波形图.

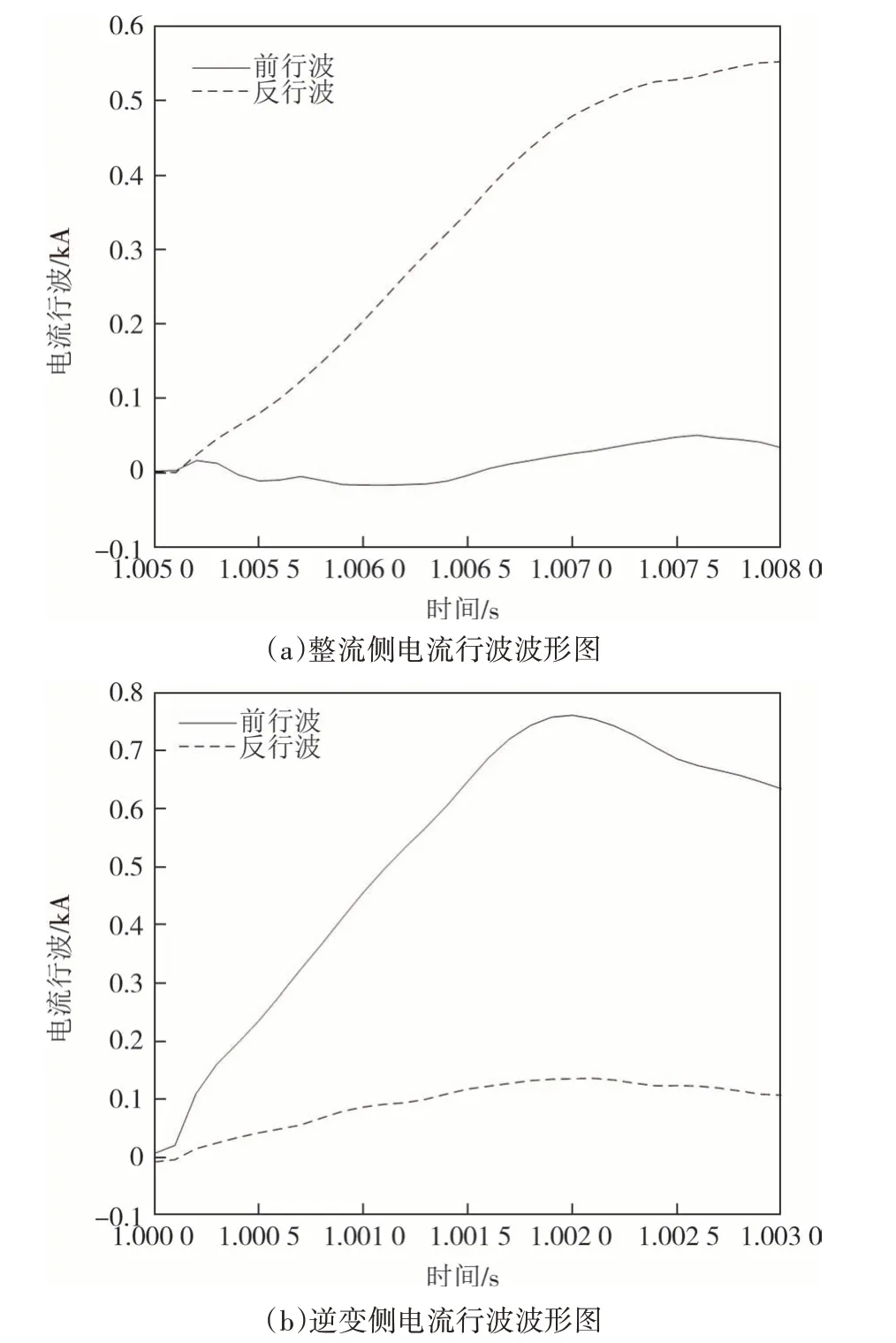
图7 逆变侧区外故障电流行波波形图Fig.7 Waveform diagram of current traveling wave during an external faults occurs on the inverter side

由图7 可知，在3 ms 数据窗时间内，整流侧（远故障端）检测到的电流反行波的幅值大于电流前行波，逆变侧（近故障端）检测到的电流前行波的幅值大于电流反行波.

4.2 区内、外故障高频能量仿真结果分析

对图1所搭建的模型分别设置不同的故障f1～f7，并对每种故障分别设置过渡电阻（0 Ω、100 Ω、200 Ω、300 Ω、400 Ω、500 Ω）进行仿真.通过小波包变换采集整流侧和逆变侧保护安装处的1 模高频前行波能量E1q和1 模高频反行波能量E1f，结合区内、外保护判据进行判别，仿真判别结果如表3 和图8所示.

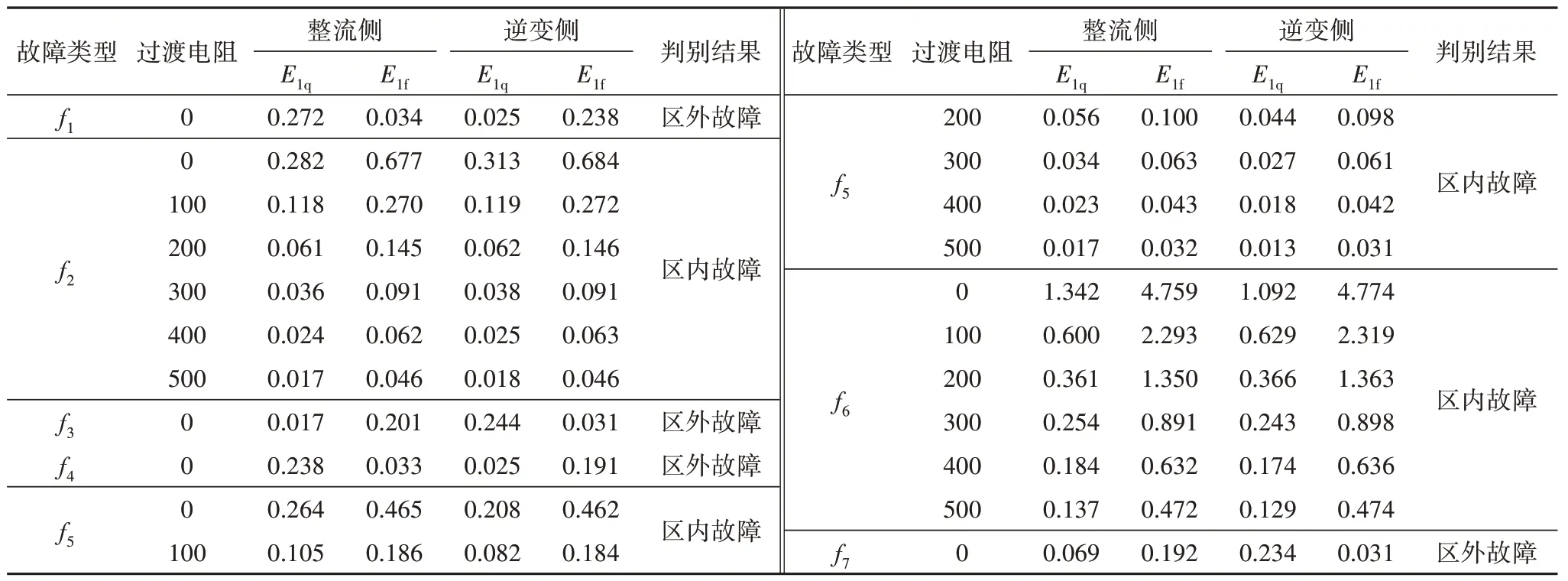
表3 区内、外故障仿真结果分析Tab.3 Analysis of fault simulation results inside and outside the line

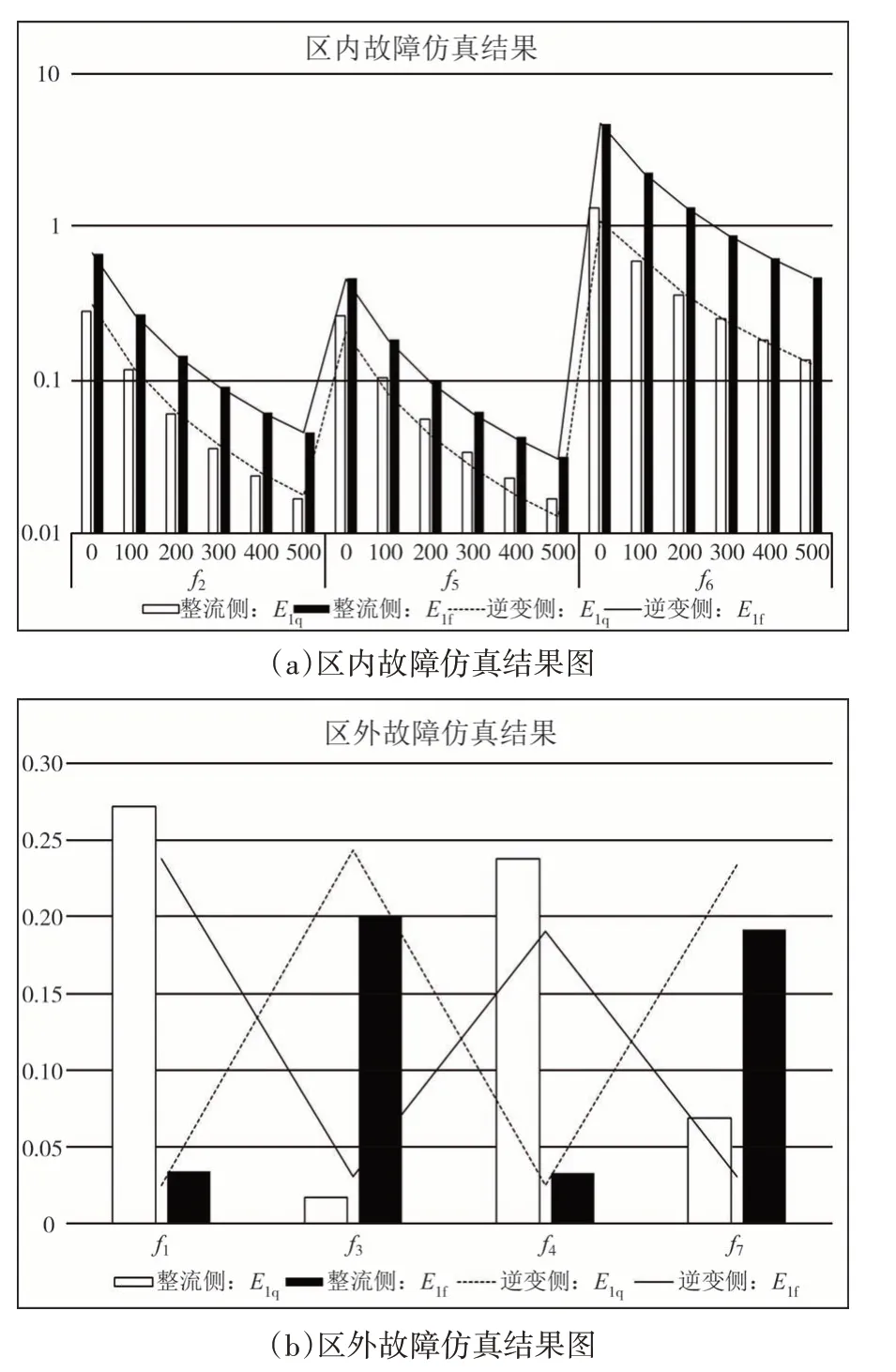
图8 区内、外故障仿真结果图Fig.8 Simulation results of internal faults and external faults

由表3 和图8 可以看出，当故障发生为图1 中f2、f5，f6时，其整流侧和逆变侧均有E1f＞E1q，此时判别为区内故障，保护动作；当故障发生为图1 中f1和f4时，其整流侧有E1f＜E1q，逆变侧有E1f＞E1q，此时判别为整流侧区外故障，保护不动作；当故障发生为图1 中f3和f7时，其整流侧有E1f＞E1q，逆变侧有E1f＜E1q，此时判别为逆变侧区外故障，保护不动作.

综上所述，保护方案区内、外识别结果准确，识别判据可有效识别区内、外故障，并且具有一定的耐过渡电阻能力.

4.3 故障选极仿真结果分析

由4.2节判别出区内故障后，继续对区内线路故障进行选极判别.以故障发生在距离整流侧750 km时的故障为例，对区内故障的f2、f5、f6分别设置过渡电阻（过渡电阻值同上节）进行仿真.通过小波包变换分别采集整流侧正极、负极保护安装处的高频前行波能量和高频反行波能量以及逆变侧正极、负极保护安装处的高频前行波能量和高频反行波能量，并分别计算整流侧和逆变侧k值（计为kM和kN），结合选极判据进行判别，仿真判别结果如表4和图9所示.

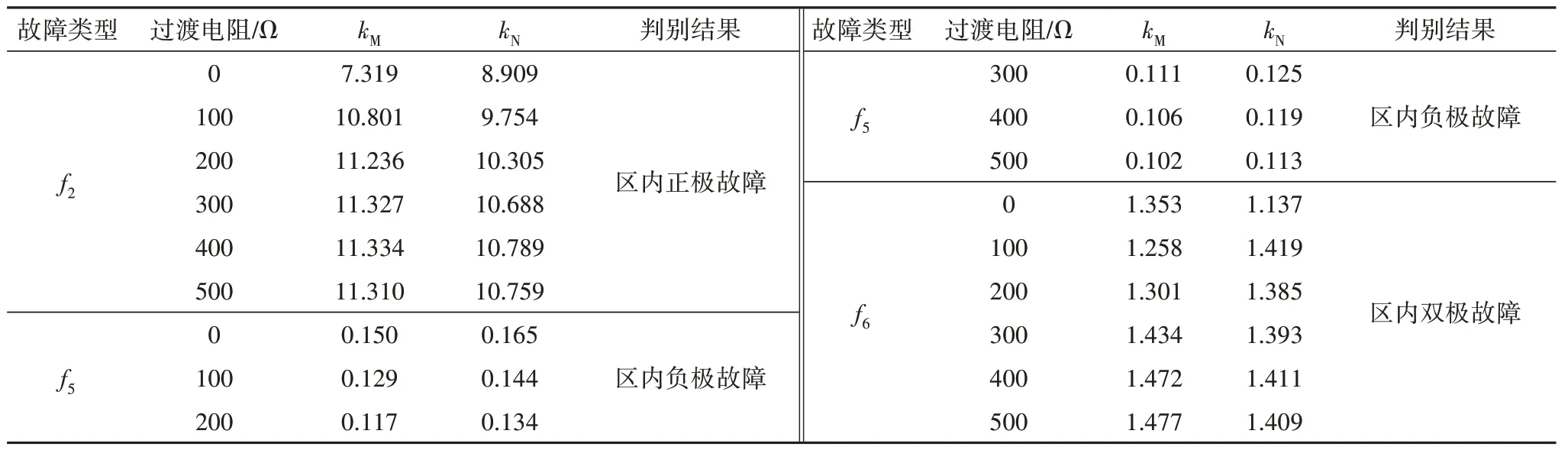
表4 区内故障选极故障仿真结果分析（750 km）Tab.4 Analysis of simulation results of fault pole selection fault in the area（750 km）

图9 故障选极仿真结果图Fig.9 Simulation results of fault pole selection in the area

由表4 和图9 可以看出，当故障发生为图1 中f2时，k值均大于1.8，判定为正极故障；当故障发生为图1中f5时，此时k值均小于0.7，判定为负极故障；当故障发生为图1 中f6时，此时k值均小于1.8 且大于0.7，判定为双极故障.

综上所述，保护方案选极判别结果准确，故障选极识别判据可有效选极，并且具有一定的耐过渡电阻能力.

4.4 不同故障距离影响仿真结果分析

为了研究故障发生的距离位置对所提出的保护的影响，对区内故障的f2、f5、f6分别设置在不同距离位置的故障（距离整流侧10 km、150 km、375 km、1 125 km、1 350 km、1490 km）进行仿真（距离整流侧750 km故障的情况已在4.2节中详细叙述，在此不再赘述），通过小波包变换分别采集整流侧正极、负极保护安装处的高频前行波能量和高频反行波能量以及逆变侧正极、负极保护安装处的高频前行波能量和高频反行波能量，并分别计算整流侧和逆变侧k值（计为kM和kN），结合选极判据进行判别，仿真判别结果如表5和图10所示.

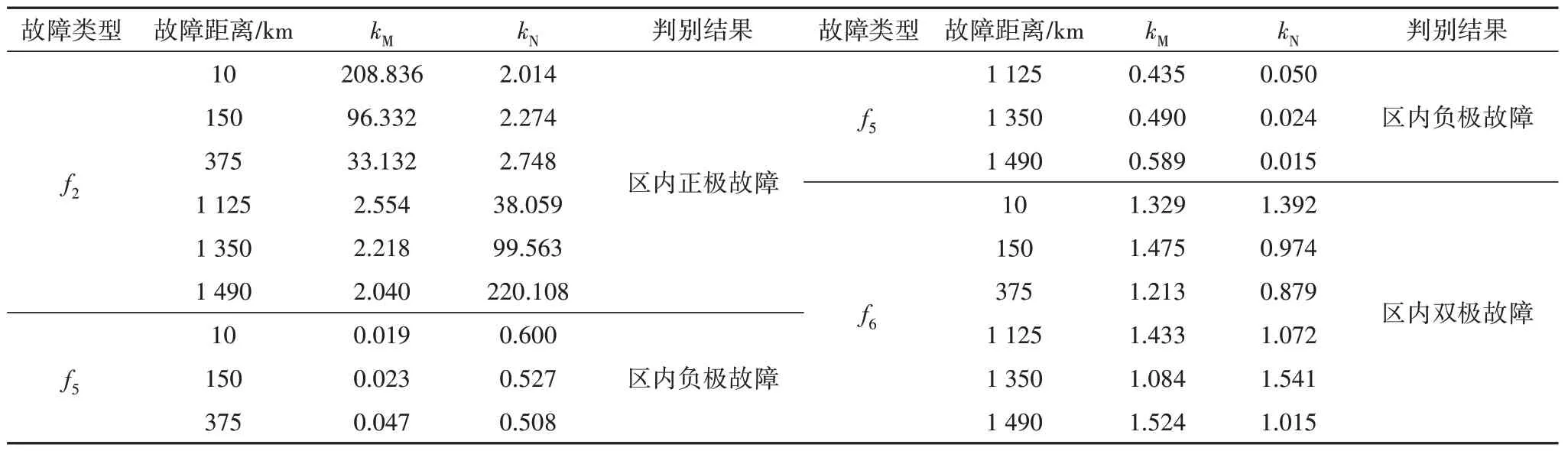
表5 不同故障距离仿真结果分析Tab.5 Analysis of simulation results of different fault distances

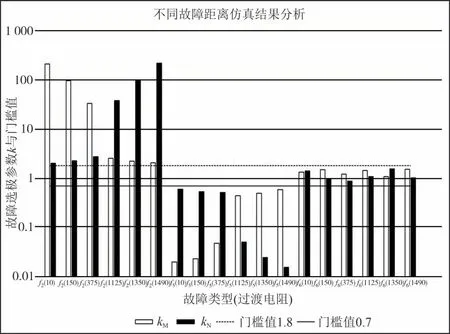
图10 不同故障距离仿真结果图Fig.10 Simulation results of different fault distances

由表5和图10可知，系统在不同故障类型时，以及分别在不同故障距离下的k值均处于设定的选极算法门槛值范围区间中，故所提出的保护对于在不同的故障类型下，处于不同距离的故障同样均具有正确识别故障方向和故障极的能力.

4.5 噪声影响仿真结果分析

在信号处理过程中，一般会出现噪声从而产生干扰，这种干扰一般用信噪比来衡量，信噪比越小，说明其噪声干扰越强.对区内故障的f2、f5、f6分别加入20～40 dB 的高斯白噪声，通过小波包变换分别采集整流侧正极、负极保护安装处的高频前行波能量和高频反行波能量以及逆变侧正极、负极保护安装处的高频前行波能量和高频反行波能量，并分别计算整流侧和逆变侧k值（计为kM和kN），结合选极判据进行判别，仿真判别结果如表6和图11所示.

表6 不同噪声下仿真结果分析Tab.6 Analysis of simulation results under different noises

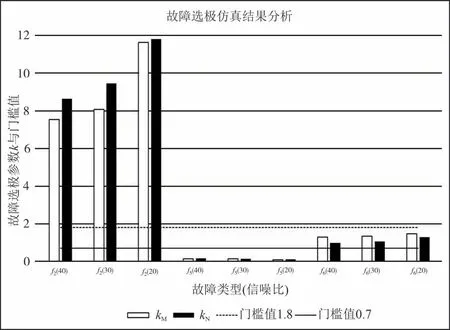
图11 不同噪声仿真结果图Fig.11 Simulation results of different noises

由表6和图11可知，系统在不同故障类型时，以及20～40 dB 下的k值均处于设定的选极算法门槛值范围区间中，故所提出的保护具有20 dB的抗噪声干扰能力.

5 结论

本文通过对前行波和反行波在直流输电系统中的传播特性的分析，结合平波电抗器大电感和直流滤波器对前反行波幅值和高频能量的影响，利用小波包变换来提取行波高频能量，提出了一种基于前反行波高频能量差异的LCC-MMC 混合双极直流输电系统纵联方向保护原理.经理论分析和仿真验证得如下结论：

1）由分析和仿真可知：当整流侧和逆变侧均有反行波高频能量大于前行波高频能量时，可判别为区内故障，保护动作；当一侧前行波高频能量大于反行波高频能量，另一侧反行波高频能量大于前行波高频能量时，可判别为区外故障，保护不动作.满足保护动作选择性要求.

2）PSCAD 和MATLAB 仿真结果表明：该保护方法能够正确可靠地识别区内、外故障，并且可正确对故障极进行选择，可靠性高.且具有一定的耐过渡电阻能力和抗噪声能力，可耐过渡电阻500 Ω 和20 db的噪声干扰，满足保护灵敏性要求.

3）本文所提方法仅需时间窗为3 ms 的数据便可进行故障判别，满足速动性要求，且数据窗存在进一步缩短的可能.

4）本文所提方法为纵联方向保护，与目前传统直流线路纵联差动保护原理的区别在于，纵联差动保护为稳态时动作，而本文所提纵联方向保护是暂态保护.并且本文所提保护仅需传输线路两端前行波和反行波的高频能量差异的判别结果，无需双端数据同步，易于硬件实现，其在故障后动作速度快，时间短，速动性上明显优于传统纵联差动保护.