导线倾角与覆冰过程扭转因素对覆冰形状特性影响研究

周超 ，孟凡泽 ，黄钢 ，姬昆鹏

（1.华北电力大学 电站能量传递转化与系统教育部重点实验室，北京 102206；2.华北电力大学 河北省电力机械装备健康维护与失效预防重点实验室，保定 071003；3.中国电力科学研究院，北京 100192）

输电导线重覆冰导致的输电线路倒塔、断线及舞动等次生危害时有发生，对跨区域输电造成严重威胁［1-3］.由于覆冰环境因素、导线自身运动特性的复杂性，现有实验及预测模型仅限于准静态导线，较少涉及运动导线覆冰形状数值模拟计算［4-5］.因此，亟需建立考虑扭转因素的输电导线覆冰预测模型.

覆冰模型主要分为三类：经验模型、理论模型和数值计算模型［6］.Langmuir 等［7］研究了水滴在无限长圆柱体上的运动轨迹，提出水滴碰撞系数概念.Makkonen 等［8］通过研究覆冰表面热平衡过程建立覆冰时变物理模型，结合导线直径、风速、温度等环境参数确定了导线覆冰质量与时间的函数关系.Myers等［9］提出基于润滑理论的水膜流动模型，研究了冰层内部的传热效应。Fu 等［10］利用边界单元法建立简化二维圆柱导线覆冰仿真计算模型，并计算了导线局部水滴碰撞系数。蒋兴良等［11］提出覆冰预测最优时间步长模型，研究了风速、温度等气象参数对雾凇覆冰质量和冰形的影响.侯硕等［12］基于润滑理论建立了任意二维截面上积冰数值模型，并与Messinger 模型预测结果进行了对比.刘春城等［13］建立雨凇覆冰模型，研究了覆冰质量与水滴中值直径、风速及导线直径等参数随时间的变化规律.梁曦东等［14］利用边界单元法建立了导线时变覆冰预测模型，计算时可以针对覆冰过程中环境参数的变化进行更新.何青等［15］提出考虑碰撞系数、焦耳热和导线表面温度的冻结系数计算方法，并指出考虑碰撞系数和导线表面温度使得冻结系数变大.周超等［16］建立了三维时变导线覆冰预测模型，基于多步积冰算法计算得到的覆冰预测精度较单步积冰算法提高8%.

覆冰过程中，导线受覆冰偏心和风载荷等的影响，容易发生扭转位移.导线扭转后，由于冰形的影响，等效直径增大，可捕获更多水滴，覆冰冰形由单侧覆冰逐渐转变为近似圆形［17］.韩兴波等［18］研究发现，相同冰期内导线中心点扭转角度最大，两端最小且呈对称分布.樊社新等［19］对不同覆冰厚度导线扭转刚度进行实验测量，使用最小二乘法得到了导线扭转刚度随冰厚变化的公式.李嘉祥等［20］提出了一种考虑覆冰偏心的分裂导线扭转刚度计算方法，认为不均匀的覆冰会对导线扭转刚度有显著影响.傅观君等［21］实验研究发现，分裂导线覆冰具有强不均匀性的特点，且随着覆冰厚度的增加，不均匀性更加明显.胡琴等［22］对比了分裂导线和单导线的覆冰扭转特性，发现分裂导线扭转角度仅为单导线的10.2%.

准确预测导线覆冰扭转后的冰形，对预防线路灾害具有重要意义，现有研究较少考虑导线扭转覆冰时冰形的演变过程.因此，本文通过考虑覆冰偏心、风速等对导线的耦合扭转特性以及冰形对导线扭转过程中刚度的影响，建立导线动态扭转覆冰预测模型，并与实验数据对比.基于新建立的预测模型，研究导线不同倾斜角度下冰形的变化及温度、风速等环境参数对导线扭转速度的影响.

1 导线覆冰扭转计算模型

1.1 导线覆冰计算

1）空气流场计算

空气流场计算采用基于RNG（重整化群）方法的k～ε湍流模型，该模型对覆冰导线空气流场计算具有较高的精度［23］.将导线周围的流场看作黏性不可压缩的流体，使用N-S 方程计算空气流场的速度分布［24］，即

2）过冷水滴碰撞轨迹计算

在流场中，过冷水滴在碰撞导线的过程中受到多种力的作用［25］，可表示为

式中：FN为水滴所受拖拽力，FG为水滴自身重力，Ff为水滴所受气流的浮力，FM为其它作用力.使用欧拉法求解气液两相流模型，得到水滴在流场中的速度分布，进而求得导线各位置的局部水滴碰撞系数.局部水滴碰撞系数［26］定义为

式中：dY是流场中相邻两条水滴流径的垂直距离，dL是捕获的相邻水滴在导线表面相隔的长度.实际导线覆冰的环境中，水滴直径大小不唯一，根据文献［10］数值模拟时使用水滴中值直径（MVD）进行计算，水滴分布模型为Monodisperse.

3）导线表面结冰计算

过冷水滴在导线表面经过对流、蒸发、升华和凝固等热量传递后冻结成冰，整个过程中能量守恒.基于导线表面的热交换过程，建立能量守恒方程［27］，表示为

式中：LWC 为液态水含量；hf为水膜高度，cf和cs为水和冰的比热容，Levap和Lfusion为水的蒸发潜热和冰的融化潜热，E∞和Ef为流场温度和水膜温度，为液滴运动速度和壁面局部液滴撞击速度，T∞和Tf为环境温度和覆冰表面温度，Q为防冰热通量.

覆冰密度与环境温度、风速、液态水含量等环境参数有关，根据文献［24］采用Makkonen-Stallabrass密度模型，计算式为

其中RM为计算参数，其表达式为

1.2 覆冰扭转控制方程

覆冰开始后，导线在耦合力矩的作用下发生扭转.对于长度为N的导线，将其等分为2n+1 个节点，中间节点为N0.相邻节点间长度为x，如图1所示.

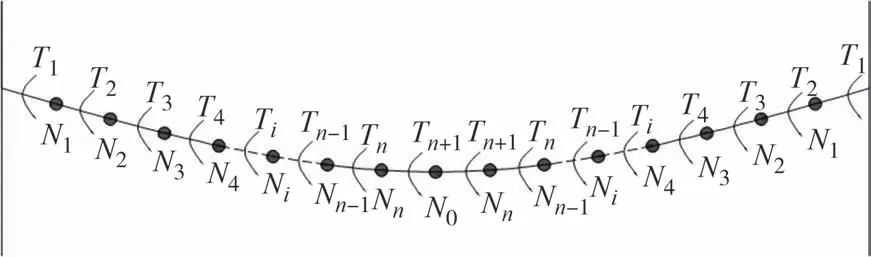
图1 导线扭转示意图Fig.1 Schematic diagram of conductors torsion

在对称的情况下只需计算其中一半节点的扭转角度，控制公式为［28］

式中：k为时间步，i为节点坐标，j为力矩坐，G为导线剪切强度，为导线覆冰后转动惯量，ΔTn为不同时间步作用于导线的扭转力矩增量.各参数计算式为

2 数值计算模型验证

2.1 流场建立

根据文献［10］，覆冰计算时将钢芯铝绞线简化为圆柱体，数值模拟使用Fluent 及Fluent Icing 完成.流体域为大小20D×20D×40D（D为输电导线直径）的三维计算域，导线距速度入口及上下边界的距离均为10D.为提高覆冰计算的准确度，在导线表面使用适于流体计算的膨胀网格，并对速度入口处网格进行了加密.网格划分如图2 所示，计算域边界面参数见表1.

表1 流场边界参数

图2 流体模型网格设置Fig.2 Mesh settings of the fluid model

图3 为导线覆冰扭转计算流程.与静态导线相比，导线扭转后其周围空气流场和水滴碰撞导线的轨迹随之发生变化.

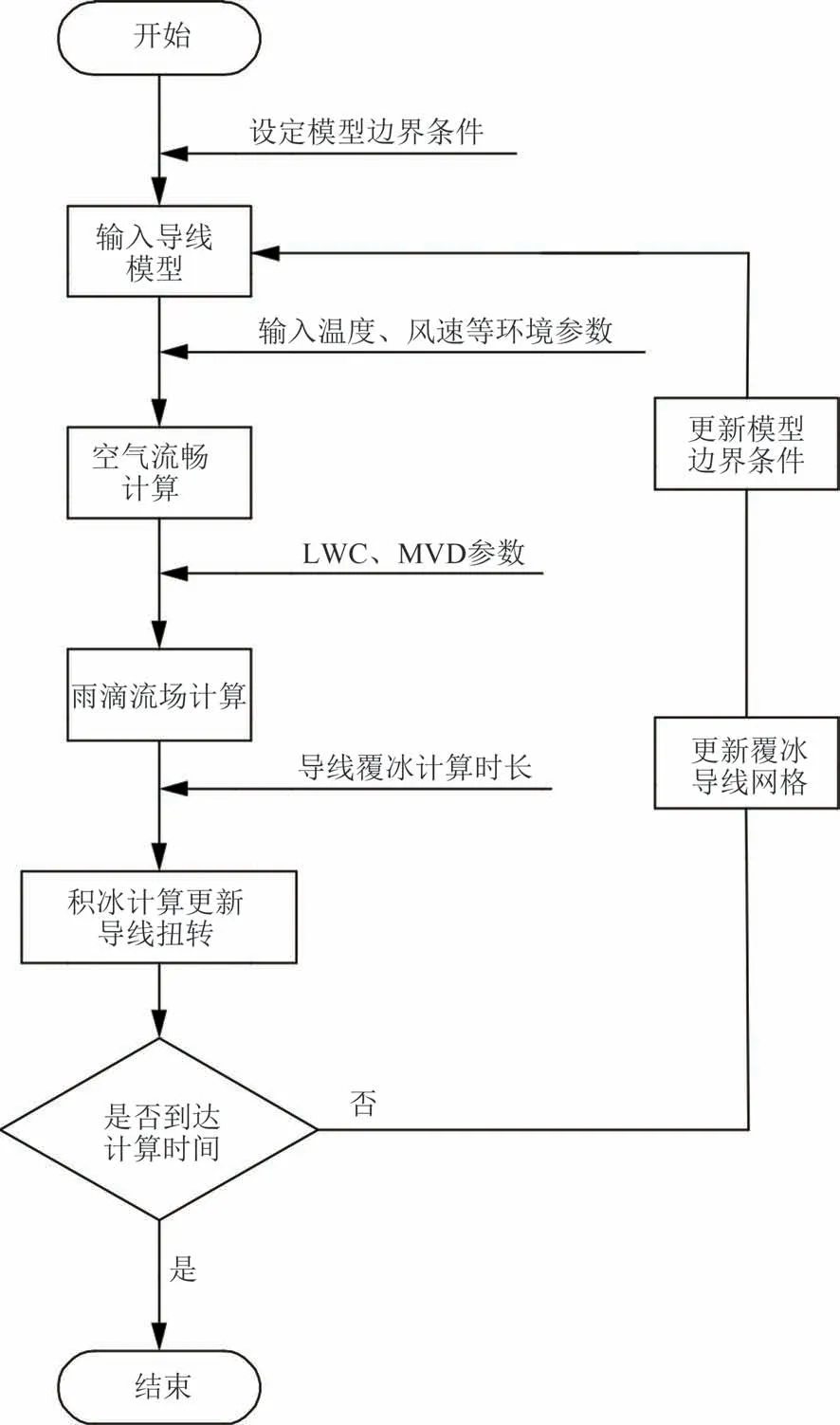
图3 导线覆冰扭转计算流程图Fig.3 Flow chart of conductor icing torsion calculation

时间步长ts的选择影响到覆冰计算的精度和效率，根据文献［11］选定单步步长为360 s，此时覆冰冰形准确度与实验吻合度较好.由图3 可知，计算时，首先对模型的初始边界条件及风速、温度、液态水滴浓度及MVD 等外部环境参数进行设定.由设定的环境参数对导线外部的空气流场和水滴碰撞轨迹进行计算，获得导线壁面的水滴收集效率.根据所得的水滴收集效率，通过式（5）、式（6）求解得到导线各节点的冰形和覆冰质量，从而得到导线不同位置处覆冰质心的坐标.将上述计算所得覆冰质量、冰质心和风速等相关参数代入式（9）、式（10），得到导线覆冰后各节点所受耦合扭转力矩，从而根据式（8）获得导线各节点扭转角度并加以修正.总覆冰时长范围内，每完成1 个时间步的计算后，需对扭转后的覆冰导线重新划分网格，并对模型边界条件及外部环境参数进行更新.重复迭代上述计算过程，直至到达计算所设定的总覆冰时长.

2.2 覆冰仿真模型验证

为验证本文导线覆冰计算方法的有效性，对文献［17］所做导线覆冰扭转风洞实验进行验证.实验记录了导线在不同时刻的扭转角度，并分别在第125 min、245 min、363 min和444 min 4个时间节点提取了导线覆冰后的冰形，导线的扭转角度分别为140°、223°、263°和291°.文献［28］采用时不变参数对实验进行了模拟，实验及文献相关参数见表2.

表2 覆冰扭转实验及文献［28］相关参数

图4 为上述4 个扭转角度下数值模拟导线中间节点（0.22 m 长度处）冰形与文献［17］、文献［28］冰形的对比.对比发现，扭转角度为140°时数值模拟覆冰面积相比文献［17］中导线覆冰面积大16.8%，其余3 种角度下数值模拟结果比文献［17］小13.75%、9.56%、7.54%.同文献［28］相比，4种扭转角度下数值模拟计算得到的覆冰截面积精度分别提高36.60%、42.21%、-7.3%和6.0%.

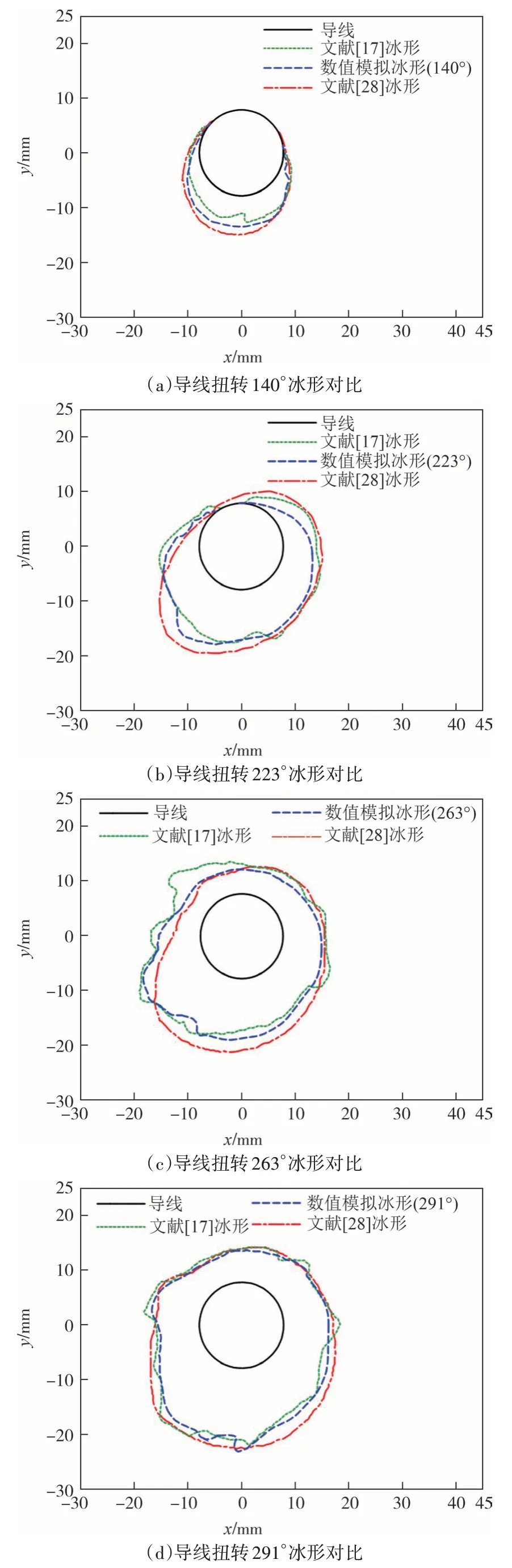
图4 不同扭转角度下覆冰形状对比Fig.4 Comparison of ice cover shapes at different torsion angles

分析图4 可知，导线覆冰扭转角度为140°时，数值模拟所得覆冰在导线表面覆盖面积较文献［17］大6.45%，与文献［28］相比，准确度提高11.35%。数值模拟所得覆冰面积大于文献［17］所得，原因是覆冰早期冰质量较小，风载荷力矩对导线扭转影响较大，模拟中风载荷力矩小于实验中的实际值.随着覆冰质量增加，风载荷力矩对导线扭转的影响减弱，数值模拟所得冰形也更接近实验结果.扭转角度为223°时，数值模拟所得冰形在导线迎风面与实验冰形符合较好，迎风面下侧有突起，背风面的厚度略小于实验冰形.扭转角度为263°时，实验中导线迎风面的覆冰厚度均匀，与数值模拟所得结果相比，在迎风面下侧的覆冰厚度接近，迎风面上侧覆冰厚度较大.扭转角度为291°时，数值模拟所预测的冰形与实验得到的冰形整体拟合程度良好.覆冰过程中，数值模拟所预测的冰形与实验得到的冰形相比更为光滑.原因可解释为：实验中水滴直径及风速等环境参数的变化使得水滴与导线表面碰撞轨迹发生改变，导致实验中冰形表面凹凸程度超过数值模型.

以导线直径为19.6 mm、档距100 m 为例进行覆冰扭转模拟，相关参数如表3 所示.提取8 个不同时间点的导线中间节点（50 m 长度处）冰形进行分析，结果如图5所示.

表3 覆冰模拟参数

图5 导线覆冰扭转冰形变化Fig.5 Conductor ice covering and twisting ice shape change

分析图5 可知，导线受到覆冰偏心的作用逐渐扭转.随着数值模拟时间的增加，覆冰向背风侧移动，冰形由单侧覆冰变为近似圆形.

2.3 倾斜导线覆冰扭转计算

在役运行输电线路中，受弧垂、高差等因素影响，输电导线必然存在一定程度的倾斜.短时间内导线倾角不会对覆冰特性产生明显的影响.然而，随着覆冰时间的增加，倾斜导线下游则可能出现更多的覆冰.以表2 条件为工况参数，设置水平倾角α为30°、45°和60°典型导线倾角工况，研究导线倾角对覆冰扭转的影响，导线倾角定义见图6.导线长度为0.44 m，模拟时长为245 min，提取导线中间节点冰形进行分析.

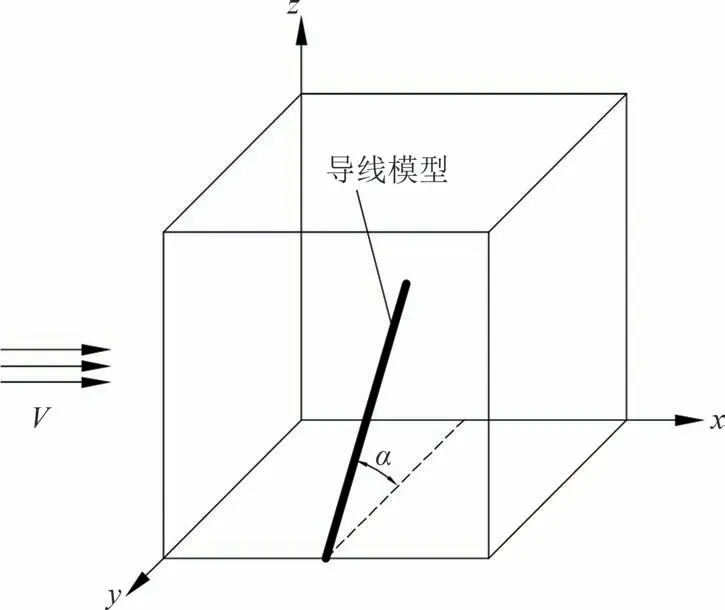
图6 导线倾角定义Fig.6 Inclination angle definition for transmission conductor

2.3.1 计算结果分析

3种工况计算结果如图7～图9所示.

图7 倾斜30°导线与水平导线冰形对比Fig.7 Comparison of tilted 30° conductor and horizontal conductor

倾斜30°导线：覆冰125 min 时覆冰扭转角度为143.6°，覆冰面积较水平导线计算结果大8.4%.覆冰245 min 时覆冰扭转角度为230.2°，覆冰面积较水平导线计算结果大15.16%.覆冰早期，30°倾斜导线与水平导线冰形相比没有明显差异.随着计算时间增加，倾斜导线迎风面的覆冰厚度较水平导线不均匀性增大.原因可解释为：未冻结的水滴在重力和气流的作用下，由导线上游向斜下方流动，更多的水滴在导线迎风面的下侧发生冻结，并累积.

倾斜45°导线：覆冰125 min 时扭转角度为146.2°，覆冰面积较水平导线计算结果大15.31%。覆冰245 min 时扭转角度为234.4°，覆冰面积相较水平导线大20.5%.与导线倾角为30°时相比，导线倾角为45°时，覆冰在迎风面下侧积累更多，覆冰在导线表面的覆盖面积更大，但整体覆冰形貌类似.

倾斜60°导线：覆冰125 min 时扭转角度为150.4°，覆冰面积较水平导线大18.26%.覆冰245 min时扭转角度为239.2°，覆冰面积较水平导线大26.3%.倾斜导线迎风面的冰形呈“沟壑”状，覆冰在迎风面上侧的厚度略小于水平导线，下侧的厚度则出现了明显的增加.

对比图7、图8 和图9 可知，覆冰时间较短时，倾斜导线和水平导线的覆冰计算结果不会出现显著差异.随着时间的增加，覆冰在导线迎风面厚度出现分化，上侧较小，下侧明显增加.导线倾斜角度较小时，冰形表面较为光滑，倾斜角度增大后，覆冰形状逐渐粗糙，并在导线的迎风面出现了“沟壑状”分层.原因可解释为：导线倾斜角度的增加使未冻结水滴受到重力、离心力和气流的影响增大，并随着水膜更快地向导线的斜下方流动，迎风面上侧的水滴减少，下侧增多，覆冰出现了分层，导致“沟壑”的出现.

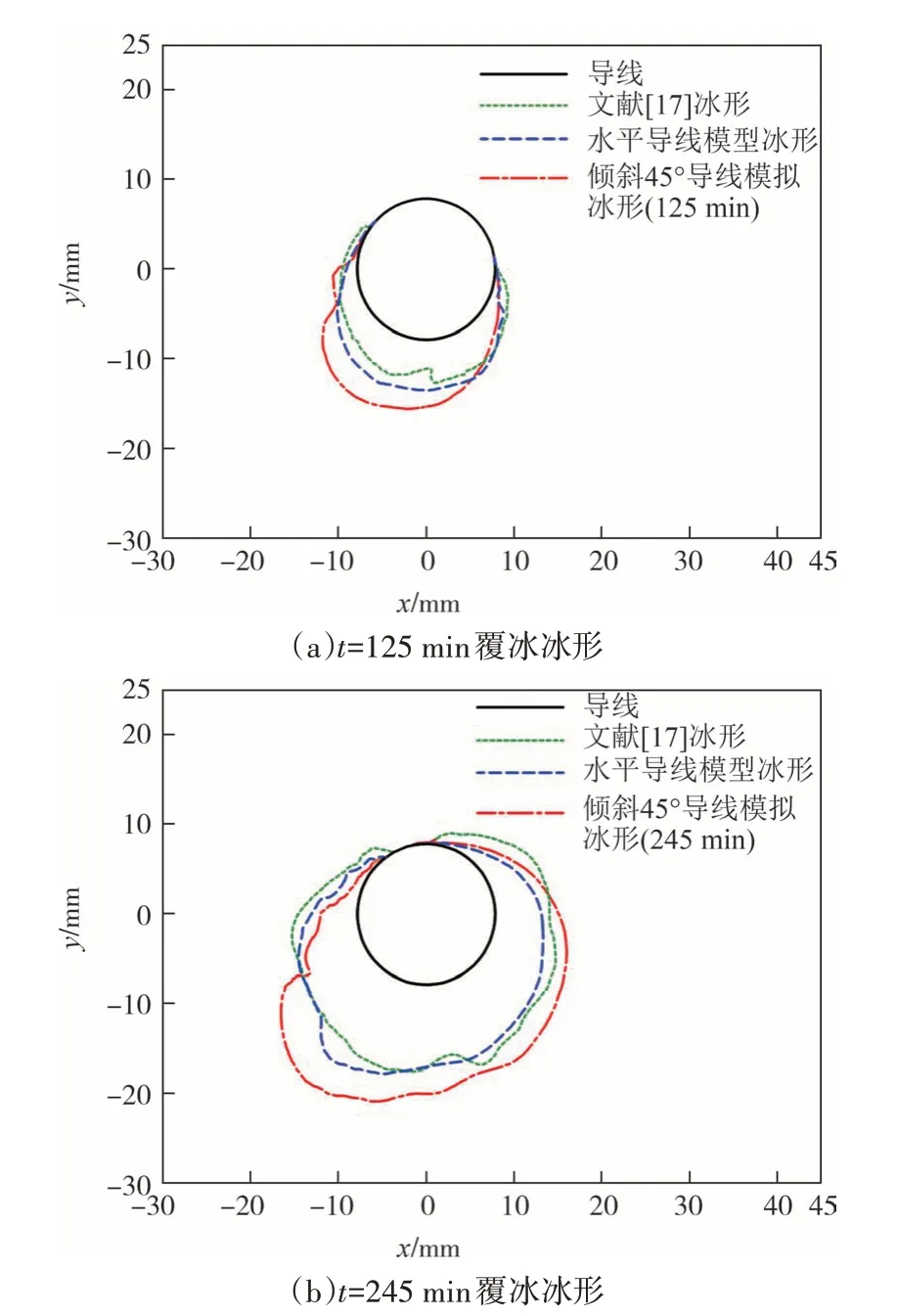
图8 倾斜45°导线与水平导线冰形对比Fig.8 Comparison of tilted 45° conductor and horizontal conductor

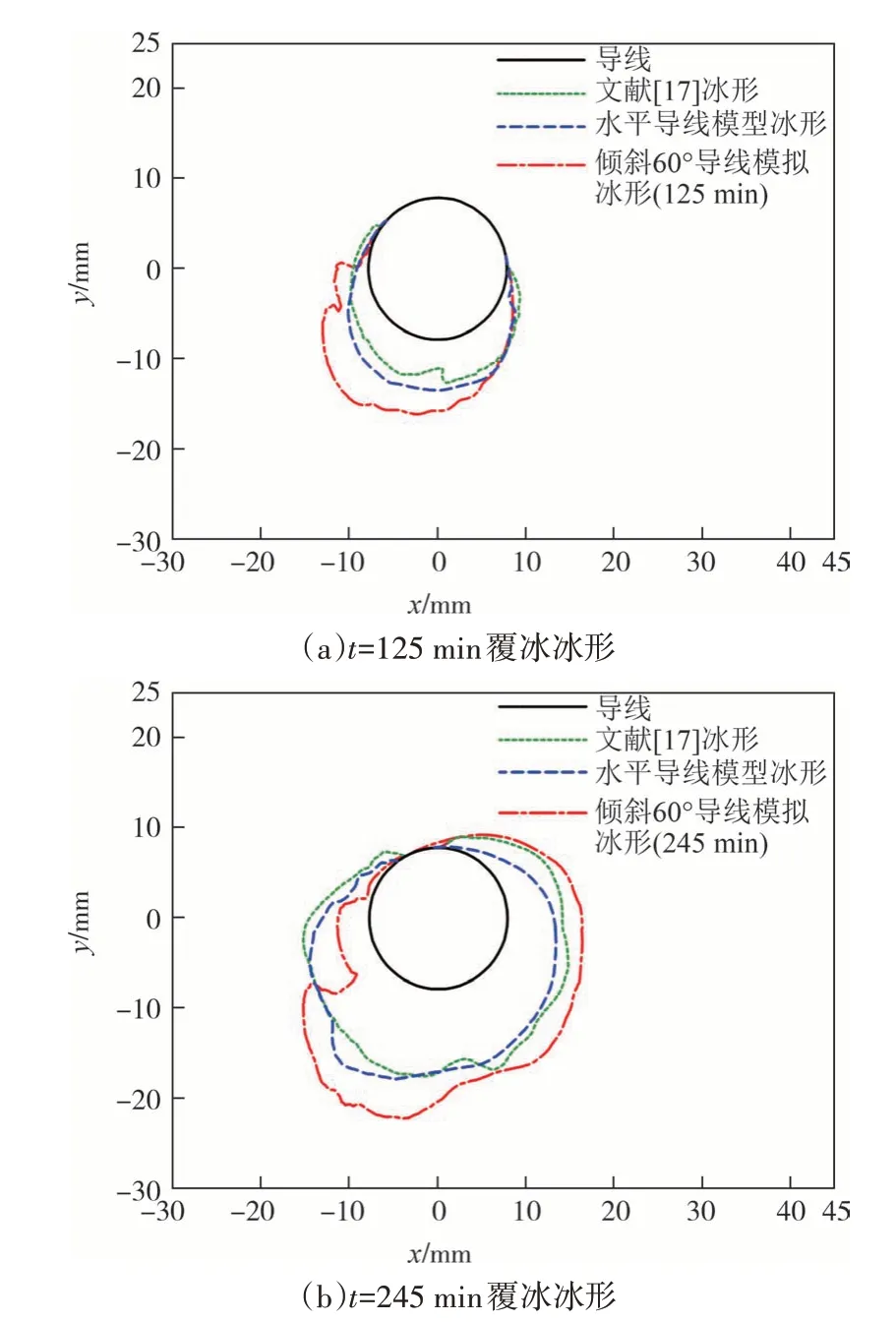
图9 倾斜60°导线与水平导线冰形对比Fig.9 Comparison of tilted 60° conductor and horizontal conductor

由中间节点向两侧各取50 mm 长导线（60°倾角）展示三维扭转覆冰形貌［29］，结果如图10 所示.覆冰125 min 时导线上游覆冰厚度较为均匀，下游迎风面下侧的覆冰厚度大于上侧.覆冰245 min 时导线覆冰厚度的不均匀性加剧，上下游覆冰均出现了分层.原因可解释为：覆冰过程中，多数未冻结水滴随着水膜的流动在导线下游冻结，使导线下游覆冰厚度更早出现分层.剩余部分未冻结水滴在流动过程中冻结，因此随着时间的增加，导线上游覆冰也逐渐呈“沟壑”状.图11 和图12 分别为图10 所示覆冰形貌左右两端冰形剖面图.

图10 倾斜60°导线三维覆冰形貌Fig.10 Three-dimensional ice topography of tilted 60°conductor

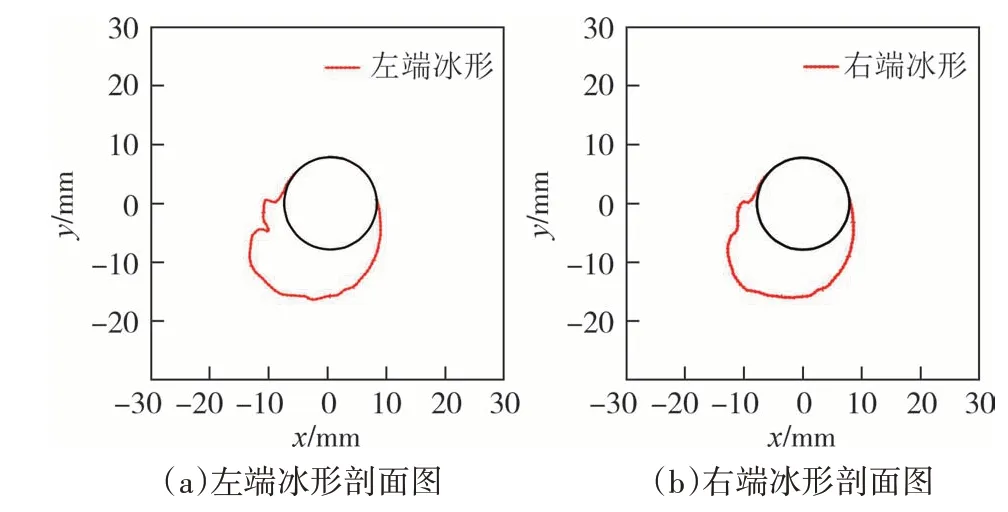
图11 覆冰125 min左右两端冰形剖面图Fig.11 Ice profile at both ends of the ice cover for about 125 min

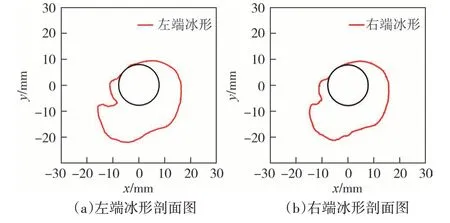
图12 覆冰245 min左右两端冰形剖面图Fig.12 Ice profile at both ends of the ice cover for about 245 min

图13 为导线覆冰扭转角度随时间变化曲线.由图中可以看出，覆冰初期水平导线及各倾斜角度导线的扭转角度差别不大.随着时间的增加，大倾角导线扭转角度相较小倾角导线更大.

图13 α=0°、30°、45°、60°导线扭转角度随时间变化曲线Fig.13 α=0°，30°，45°，60° conductor torsion angle change curve with time

3 导线覆冰扭转数值计算

导线覆冰的结果受到液态水含量（LWC）、液态水滴中值直径（MVD）、温度和风速等因素的影响［30］.环境参数的差异改变了导线的覆冰形状和质量，导致扭转过程中扭转刚度及扭转力矩发生变化，最终影响导线覆冰预测精度.以直径34.9 mm、档距100 m导线中间节点（50 m长度处）为对象，对比分析不同温度、风速、MVD影响下的导线覆冰扭转特性，不同工况下的环境参数如表4所示，结果如图14～图16所示.

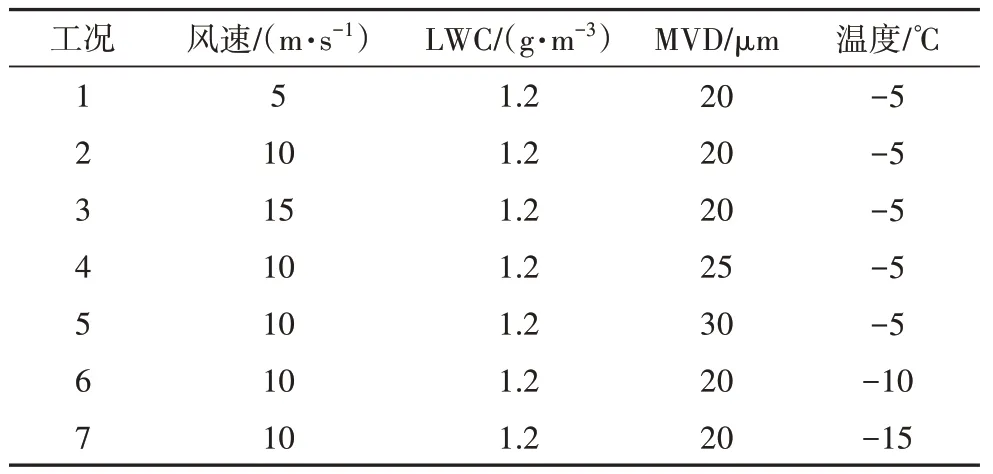
表4 覆冰工况条件参数

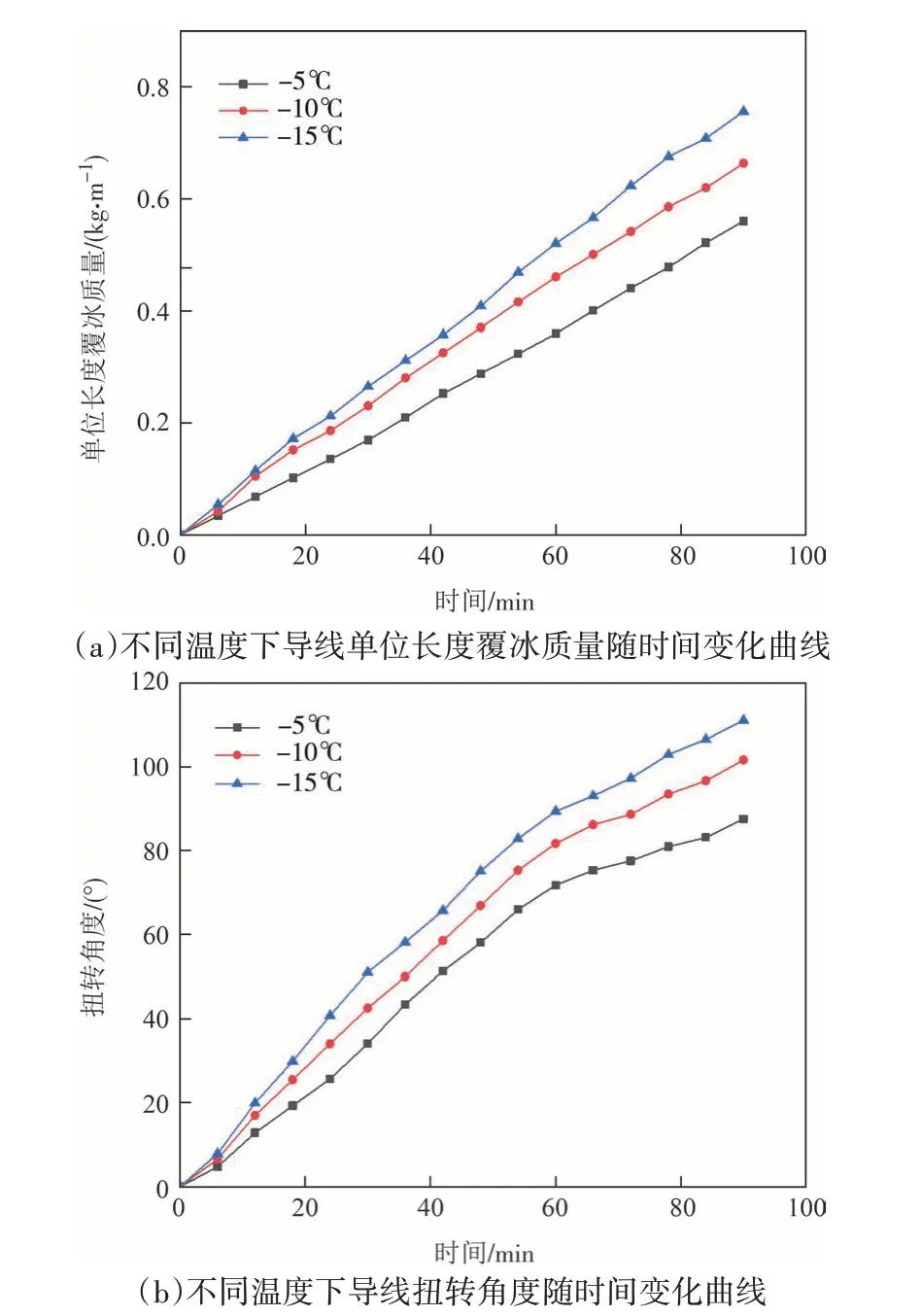
图14 温度对覆冰质量及扭转角度的影响Fig.14 Effect of temperature on ice cover mass and torsion angle

分析图14 可知，导线覆冰质量和扭转角度随着温度降低而增大.原因可解释为：温度降低使得过冷水滴在导线表面的冻结系数增大，单位时间内的覆冰质量增加，冰形外扩，覆冰重心外移.由式（10）可知覆冰质量增加及覆冰重心外移使得冰载荷力矩增加，导线扭转速度加快.但随着温度的降低，温度对冻结系数的影响效果减弱，覆冰质量增速放缓，导线扭转增速随之下降.

分析图15 可知，导线覆冰质量和扭转角度随着风速增大而增大.原因可解释为：风速增大使得相同时间内导线表面捕获的水滴数量增多，覆冰质量随之增加，导线表面覆冰由驻点位置向两侧生长，覆冰厚度增加.根据式（10）可知冰载荷力矩和风载荷力矩的增加使得导线扭转的速度加快。覆冰早期，风载荷力矩作为导线扭转的主要因素，风速增加对导线扭转速度影响更为明显.

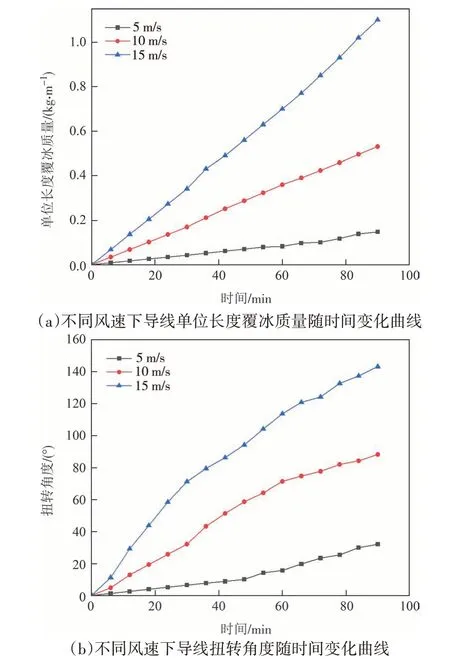
图15 风速对覆冰质量及扭转角度的影响Fig.15 Effect of wind speed on ice cover mass and torsion angle

分析图16 可知，导线覆冰质量和扭转角度随着水滴MVD 增大而增加.原因可解释为：随着水滴MVD 增大，水滴受气流扰动效应减弱，导线表面的水滴碰撞系数增加，覆冰质量和面积增大，导线的扭转速度加快.但随着水滴MVD 的增长，导线驻点位置覆冰厚度增加较少.与温度、风速等环境参数相比，对导线扭转速度的影响较弱.

图16 水滴MVD对覆冰质量及扭转角度的影响Fig.16 Effect of MVD of raindrops on ice cover mass and torsion angle

图17 为导线覆冰扭转后不同时间收集效率对比.分析可知，导线扭转后覆冰形状的变化，使导线及覆冰表面的局部水滴收集效率降低.但扭转后的导线，等效直径增大，获得更大的水滴捕获面积，整体水滴收集效率提高.工况2 条件下，随着导线扭转角度的增加，覆冰60 min 和覆冰90 min 时导线表面水滴收集效率较覆冰30 min 时分别增加6.38%和11.4%.导线扭转使单位时间内覆冰质量增加，结果如图18 所示.覆冰初期，静态覆冰和扭转覆冰的覆冰质量没有明显差异，随着覆冰时间的增加，扭转导线的覆冰质量逐渐大于静态导线的覆冰质量.

图17 不同时间导线表面液滴收集效率Fig.17 Droplet collection efficiency on the surface of the wire at different times

图18 扭转覆冰与未扭转覆冰质量随时间变化曲线Fig.18 Curve of torsional icing and untorsional icing mass with time

4 结论

本文通过考虑覆冰偏心、风速等对导线的耦合扭转特性及覆冰形状对导线扭转刚度的影响，建立了导线动态扭转覆冰模型.与文献［17］实验数据对比，验证了模型的有效性.在此基础上研究了导线倾角和温度、风速等环境参数对冰形和扭转的影响.得到的主要结论如下：

1）扭转角度为140°时，数值模拟得到的覆冰面积较文献［17］大16.8%；扭转角度为291°时，覆冰面积小7.54%。覆冰早期，导线扭转受风载荷力矩影响较大，随着覆冰质量提升，冰载荷力矩成为导线扭转的主要因素.

2）受导线倾斜角度的影响，未冻结水滴在重力、气流和离心力的作用下向导线下游移动.覆冰 245 min 时，倾斜导线覆冰面积较水平导线（α=0°）增大15.16%（倾角30°）、20.50%（倾角45°），26.30%（倾角60°）.随倾斜角度的增加，冰形呈“沟壑状”.

3）温度降低、风速及MVD 增大提高了导线表面水滴收集效率，单位时间内的覆冰质量增加，导线的扭转速度加快.风速增大还进一步提高了风载荷力矩对导线扭转的影响.

4）覆冰扭转后的导线等效直径增大，则水滴捕获面积增大.随着导线的扭转，壁面水滴收集效率相比覆冰30 min 时分别增加6.38%（覆冰60 min）和11.4%（覆冰90 min）.扭转导线单位长度覆冰质量逐渐大于静态导线.