基于频域和时域法的电池包随机振动疲劳计算对比研究

吴光强 ，李超 ，丁丰 ，章蕾

［1.同济大学 汽车学院，上海 201804；2.卡特彼勒技术研发（中国）有限公司，江苏 无锡 214000］

随着我国电动汽车的推广普及，动力电池包的振动疲劳性能已经成为制约电动汽车发展的一个重要因素.现阶段，对试制样品的振动疲劳耐久性试验校核是电池包开发流程的典型环节，但其存在研发成本高、开发周期长的缺点.如果在开发设计阶段利用计算机辅助工程（Computer Aided Engineering，CAE）技术进行产品的振动疲劳性能校核，可大大缩短研发周期、降低研发成本［1-2］.

目前，利用CAE 进行电池包随机振动疲劳寿命预测的方法主要分为时域法和频域法［3-4］.二者都包含三部分内容，即载荷作用下结构应力-应变响应历程、单个载荷循环下的疲劳损伤和疲劳损伤累积模型［5］.不同之处在于时域法是基于结构振动的应力时域信号，利用雨流计数法对结构应力实际循环次数进行统计［6］；而频域法则是基于结构振动的应力功率谱密度（Power Spectral Density，PSD）信号，利用应力幅分布模型对结构应力循环次数进行近似估计，其中Dirlik 模型是与实际情况吻合较好且应用最广泛的模型［7］.时域法由于具有较高的结构累积损伤预测精度和处理非高斯平稳随机过程的能力，被认为是与实际最为接近的一种方法［8］，但存在随机过程模拟计算量大的缺点；而频域法不需要循环计数，计算量小，其应用逐渐受到工程界的重视［9］.

在实际工程设计中，频域法和时域法虽然广泛用于对电池包振动疲劳性能的验证分析，但是有关二者的综合对比研究比较缺乏，这种缺乏会带来以下问题：

1）如果只注重频域法计算简单、快速的优势，而忽视其与时域法预测值的差距，可能会导致频域法预测的疲劳寿命值与实际寿命差距过大.

2）频域法基于振动均方根（Root Mean Square，RMS）加速度值和正态分布“3σ”原则，可能存在对电池包最大振动加速度估计不足的缺点.

为了避免类似情况的发生，本文分别利用频域法和时域法对某款动力电池包进行随机振动疲劳分析，并对二者分析结果进行对比，为频域法和时域法更好应用于工程设计提供一定参考.

1 基本理论

1.1 时域法

电池包结构振动属于线性小阻尼多自由度振动系统，其模态运动方程为：

式中：m为系统的模态质量矩阵；c为模态阻尼矩阵；k为模态刚度矩阵；q为模态坐标；Q为模态力矢量.

在时域载荷激励下，振动系统的位移响应X可由模态振型矩阵Ф和模态坐标q求出，其表达式为：

电池包结构在随机振动载荷作用下会呈现出复杂的应力应变状态，其疲劳裂纹萌生和扩展将在图1所示材料临界平面上发生，并且应力大小和方向会随构件位置和载荷作用时间不断变化［10］.

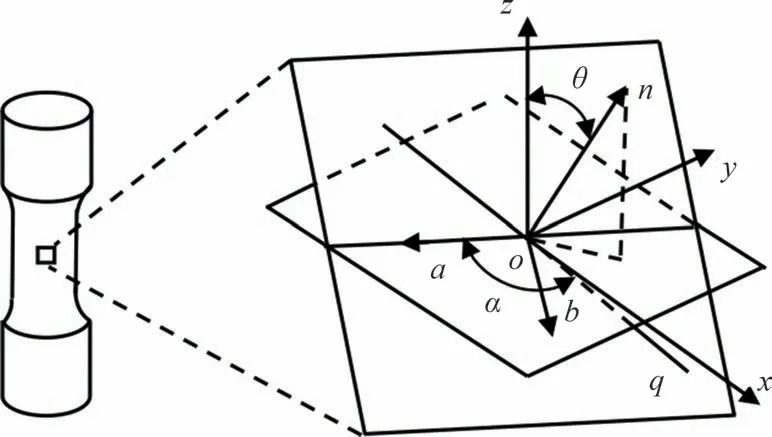
图1 材料临界面及法向nFig.1 Normal（n）of a material plane

为此，基于不同转角θ坐标系平面应力转换公式，时域法通过对不同转角平面应力时间历程进行计算和雨流统计，并结合材料的疲劳特性实现临界面求解和结构最大损伤时的疲劳寿命计算，应力转换公式为：

式中：σxx和σyy为平面正应力；τxy为平面切应力.

通过对空间不同方向应力状态下的结构损伤进行计算，临界面法可以准确预测复杂应力状态下的结构疲劳失效问题，因此得到工程界广泛认可［11-12］.

1.2 频域法

式（1）可转化为频域数学表达式：

式中：Sx（ω）为输入载荷PSD 矩阵；Sp（ω）为随机响应PSD 矩阵；H（ω）为频响函数矩阵；HH（ω）为H（ω）的共轭转置.

频响函数矩阵H（ω）表达式为：

当载荷以PSD 输入时，结构振动位移、加速度和应力响应均可由式（4）和式（5）求出.

在连续加载时间T内，幅值为S的结构应力循环次数N（S）由Dirlik模型式（6）和式（7）求出.

式中：E（P）为峰值概率期望.

1.3 RMS值

虽然随机振动的不确定性状态无法用振幅、频率和相位进行描述，但可用RMS 值对随机振动统计特征进行描述.

RMS 值是与结构振动能量大小有关的物理量.在时域内，振动信号x（t）的RMS计算公式为：

在频域内，振动信号x（t）的RMS 值可经PSD 谱在频率上积分求面积S后开根号求出，即

当结构振动响应服从正态分布时，基于“3σ”原则，可将3XRMS作为结构振动最大幅值的近似估计［13］.

2 电池包模型及模态验证

2.1 有限元模型

基于某型号电池包的实体结构和几何模型，建立如图2 所示的有限元模型.在建模过程中，按照不改变结构力学性能和计算精度的要求，为减小计算资源，对模型进行局部简化和修正，例如去除了较小倒角、螺栓、小圆孔等［14］.约束边界按照实车装配对安装吊耳孔进行全约束.

图2 某型号电池包实物及有限元模型Fig.2 Physical structure and finite element model

2.2 模态测试

为了验证有限元模型精度，采用LMS 模态测试系统进行电池包约束模态的敲击测试.测试系统主要由激振部分、数据采集部分和分析计算部分组成，如图3所示.

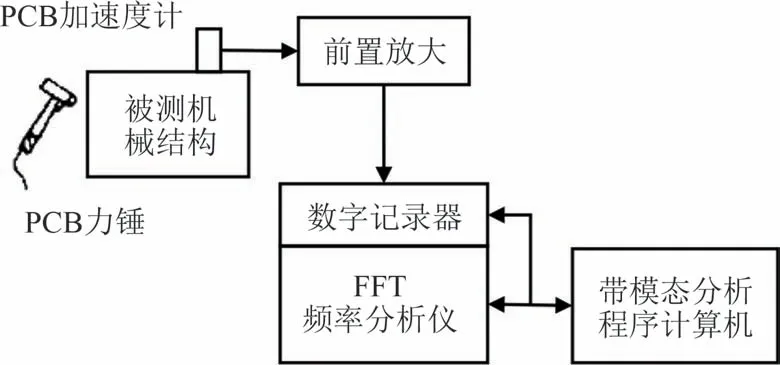
图3 LMS模态试验测试系统组成Fig.3 LMS modal test system

图中PCB 力锤对电池包进行敲击激励，LMS 数据采集仪和PCB 加速度传感器用于振动信号采集，笔记本电脑利用采集信号完成约束模态参数的识别.

此次电池包模态测试共布置了46 个振动数据采集点，采用如图4 所示的5×5 布点形式，力锤敲击点分别位于图5 所示电池包下箱体拐角、上箱盖拐角以及上箱盖中央三个位置.

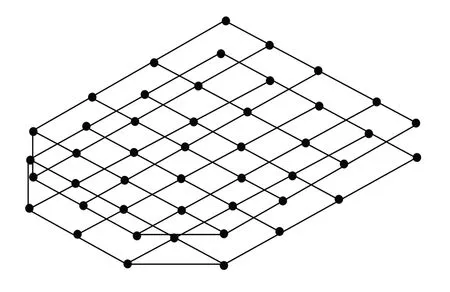
图4 电池包5×5测点布置Fig.4 Battery pack 5×5 measuring point layout

图5 模态试验力锤激励点Fig.5 Force hammer excitation point of modal test

2.3 模态验证

模态是结构的固有属性，与结构自身的材料属性、几何形状以及约束条件等有关.固有频率、模态振型是模态的两个重要特征参数［15-16］，反映了结构的刚度和质量分布，可用于有限元建模精度的验证.

1）固有频率.相似振型模态的固有频率之间的接近程度可用相对误差δ来考察［17］，其计算公式为

式中：fTest为试验模态频率；fFEA为有限元模态频率.

由表1统计的电池包前4阶模态频率值可知，有限元模态与试验模态之间的固有频率相近，相对误差均小于5%.

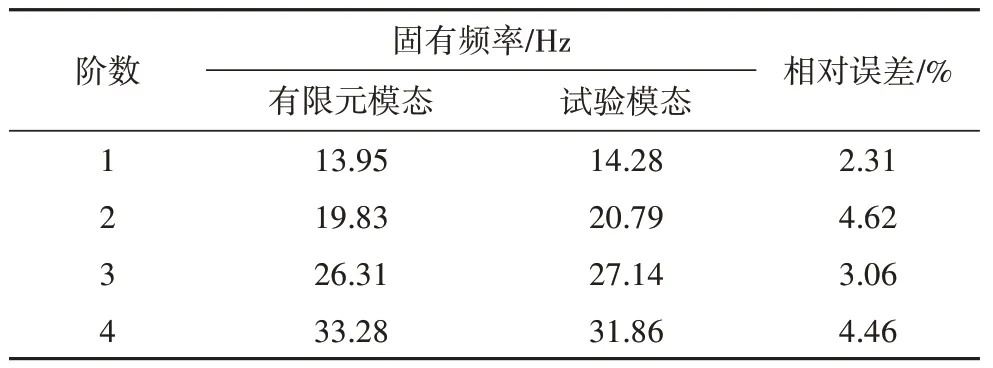
表1 电池包前4阶模态固有频率Tab.1 Natural frequency of the first four modes

2）模态振型.模态置信准则（Modal Assurance Criteria，MAC）可用于验证有限元模态振型和试验模态振型的相似程度［18］，即：MAC 值等于1，表示两个模态振型完全一样；等于0，表示两个振型不相关.其计算式为：

式中：Φej为试验模态第j阶振型向量；Φfk为有限元模态的第k阶振型向量.

图6 和图7 分别为电池包试验模态和有限元模态的前4 阶振型图，二者振型的MAC 值分别为0.93、0.86、0.89和0.87，表明同阶振型之间相似度水平高.

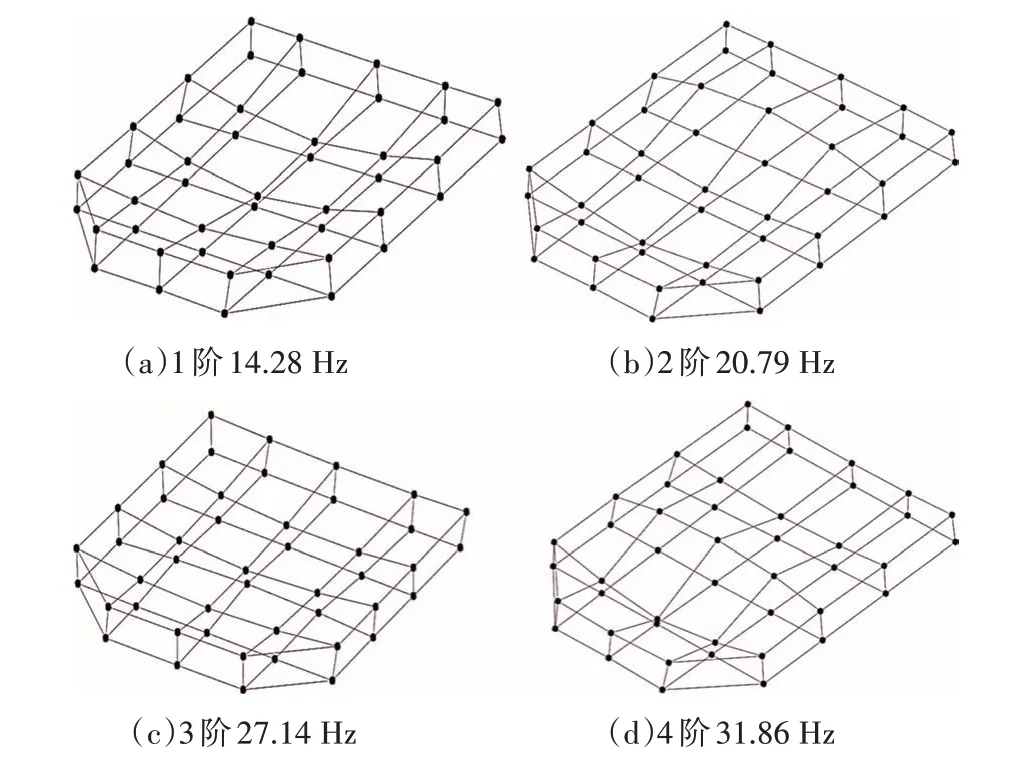
图6 电池包试验模态前4阶振型Fig.6 First 4 test modes of battery pack

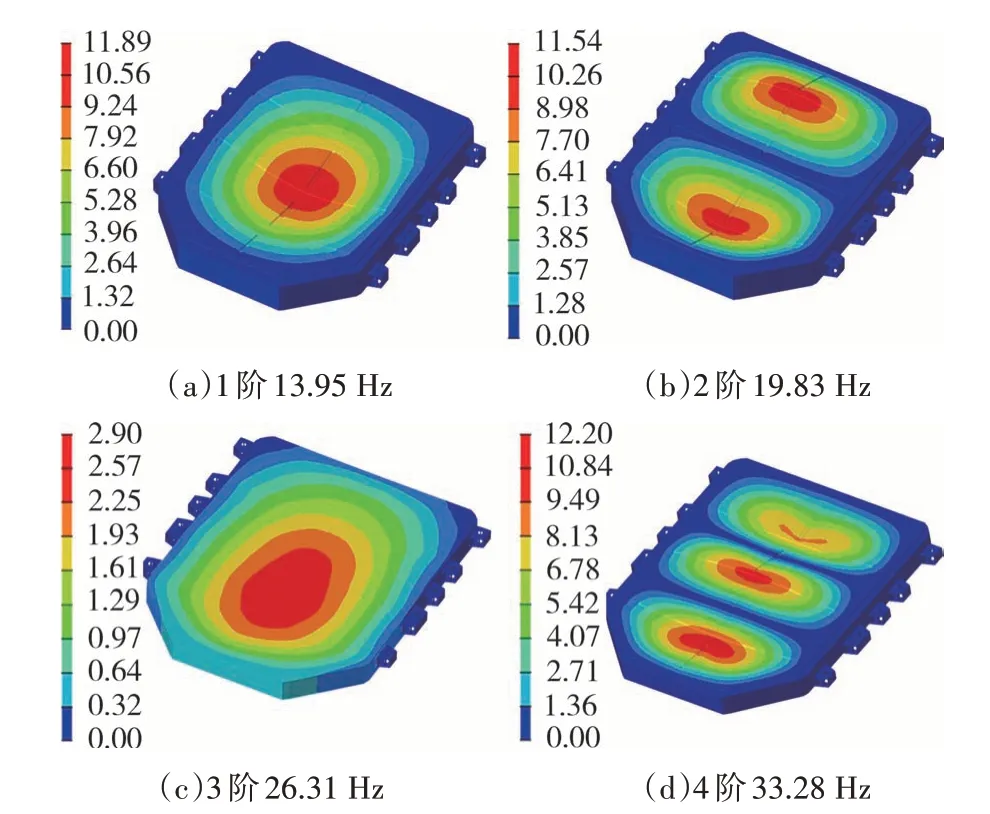
图7 电池包有限元模态前4阶振型Fig.7 First 4 finite element modes of the battery pack

由于有限元模态的固有频率和模态振型计算结果与模态试验结果相近，表明电池包有限元模型的质量分布和刚度分布与实际结构相符合，可用于随机振动疲劳分析.

3 随机振动疲劳分析

3.1 载荷的输入

输入载荷是影响时域法和频域法计算结果的重要因素，二者载荷PSD 谱统计特征相匹配是能够进行计算结果对比的前提.

频域法的输入载荷为国标GB 38031—2020 推荐加速度载荷PSD 谱，如表2 所示.基于表2 的功率谱密度值，利用傅里叶逆变换和Python 编程技术计算得到时域法的加速度输入载荷，如图8所示.

表2 频域法加速度载荷PSD谱Tab.2 Acceleration PSD load of frequency domain method

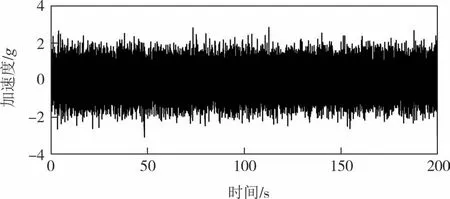
图8 加速度时域载荷Fig.8 Acceleration time domain load

由图9 所示的输入载荷PSD 曲线对比可知，时域法和频域法的输入载荷统计特征相匹配，二者的计算结果可进行对比.

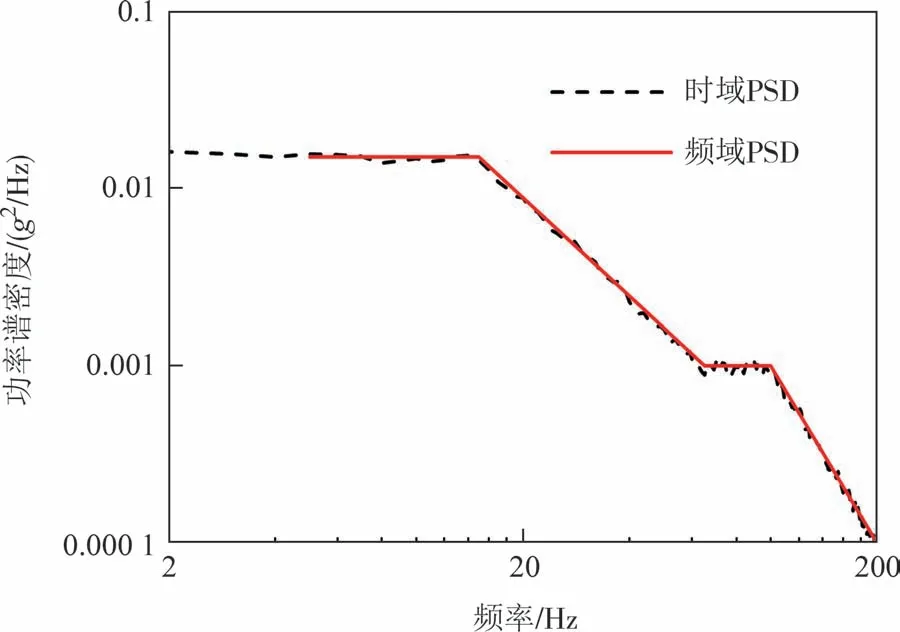
图9 输入载荷PSD的对比Fig.9 Comparison of load PSD

3.2 有限元分析计算

本文基于达索公司的ABAQUS软件，通过时域瞬态响应分析和频域随机振动分析来计算电池包有限元模型单元积分点的应力响应，并利用Python编程完成结构疲劳危险位置的寿命计算，分析流程见图10.

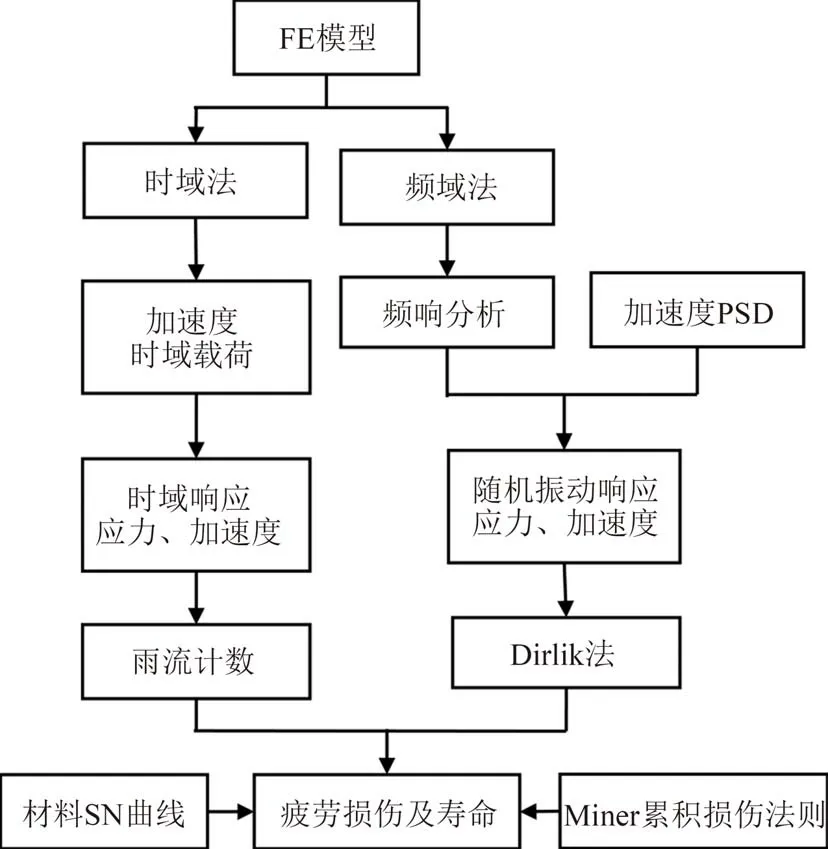
图10 随机振动疲劳CAE分析流程Fig.10 CAE analysis process of random vibration fatigue

4 结果及讨论

4.1 振动加速度

图11为频域法计算的电池包加速度RMS值分布云图.由图11可知，箱盖中央A6位置振动加速度最大.

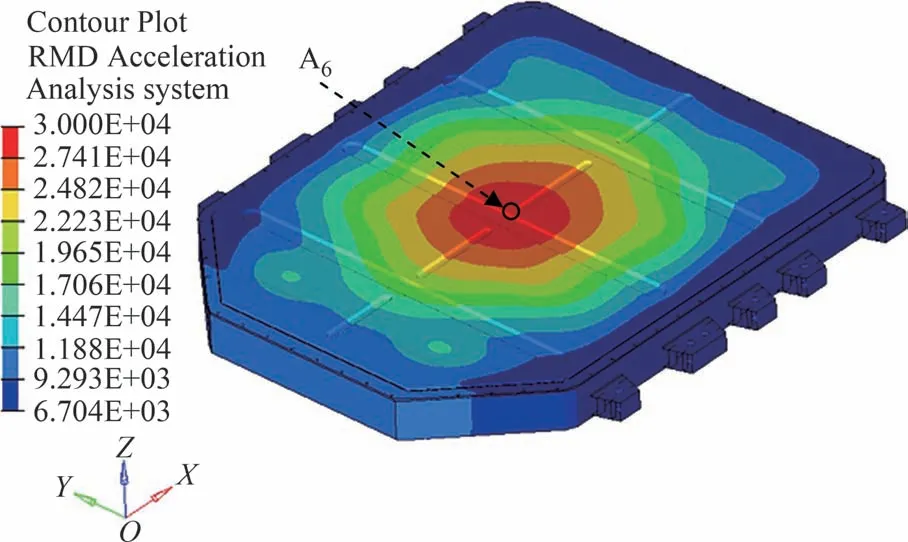
图11 频域法RMS加速度分布云图Fig.11 RMS acceleration contour of frequency domain method

为了与频域法对比，除了取箱盖中央A6测点外，另取图12 安装吊耳和模组承载梁处的A1至A5测点进行时域法分析，加速度响应结果如图13所示.

图12 时域法加速度测点位置Fig.12 Acceleration gage map of time domain method

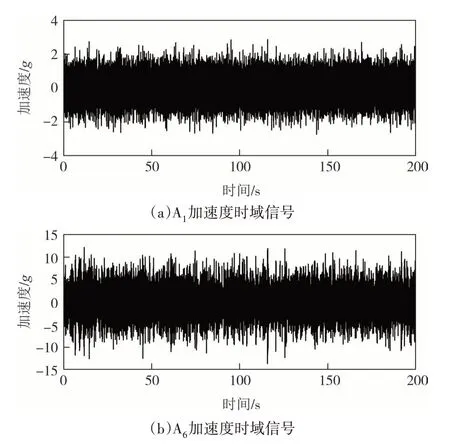
图13 加速度时域响应Fig.13 Acceleration time domain response

由表3的振动加速度统计值可知，频域法与时域法的加速度RMS值接近，最大相对误差为5.8%，表明二者所预测的电池包总振级相近；频域法“3σ”计算最大加速度与时域法最大加速度存在较大差距，相对误差范围为24.8%～30.1%，表明频域法“3σ”计算值对电池包振动最大加速度幅值的估计精度不足.

表3 结构振动加速度对比Tab.3 Comparison of structural vibration acceleration

究其原因如下：

随机振动载荷下的电池包加速度幅值服从正态分布，如表4 所示.由图14 可知，正态分布“3σ”原则的0～99%估计范围和时域法的最大加速度幅值分布范围存在较大差距.

表4 A6加速度分布统计特征值Tab.4 Statistical characteristics of acceleration distribution at A6

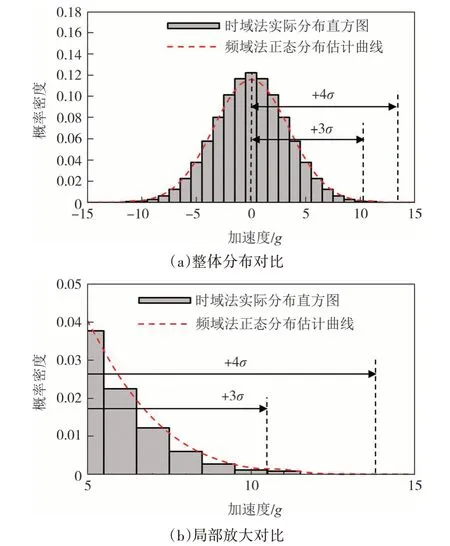
图14 A6振动加速度分布对比Fig.14 Comparison of acceleration distribution at A6

如果频域法采用“4σ”原则，计算加速度的估计范围将扩大到0～99.993 6%，与时域法的加速度最大分布范围接近，相对误差小于6.6%，见表5.

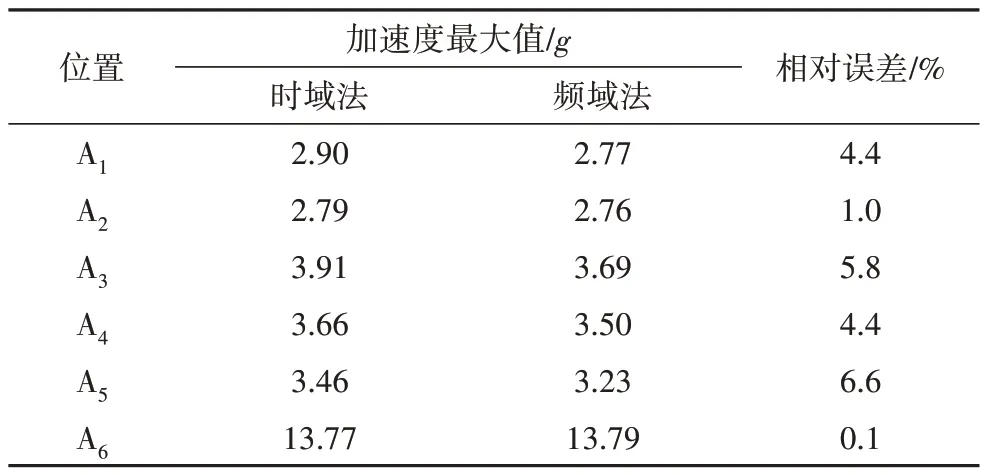
表5 频域法“4σ”计算加速度Tab.5 The“ 4σ” acceleration of frequency domain method

4.2 振动应力

利用频域法计算得到电池包箱体和箱盖的RMS应力值，分别见图15和图16.

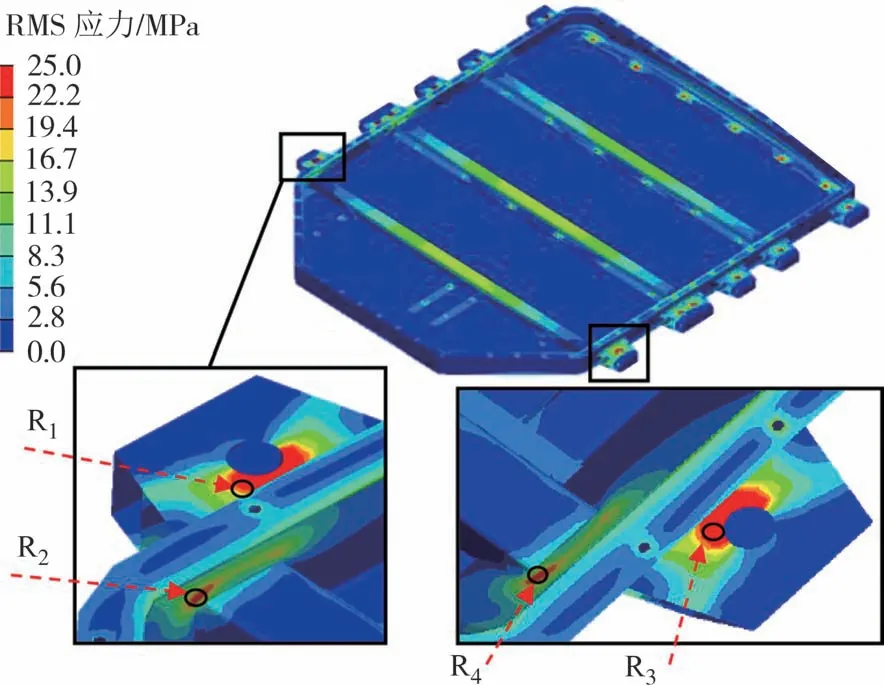
图15 电池包箱体RMS应力分布Fig.15 RMS stress contour of battery pack body

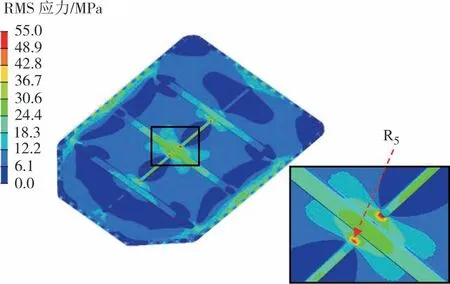
图16 电池包箱盖RMS应力分布Fig.16 RMS stress contour of battery pack cover

由图15 可知，箱体高应力区主要分布在安装吊耳孔附近、模组承载梁与侧围板连接位置；由图16可知，箱盖中央加强筋位置应力最大.

根据RMS 应力分布，利用式（3）和式（12）对图15和图16中5个危险位置的结构最大损伤应力和等效Von Mises 应力进行时域法计算，应力时域响应结果如图17和图18所示.

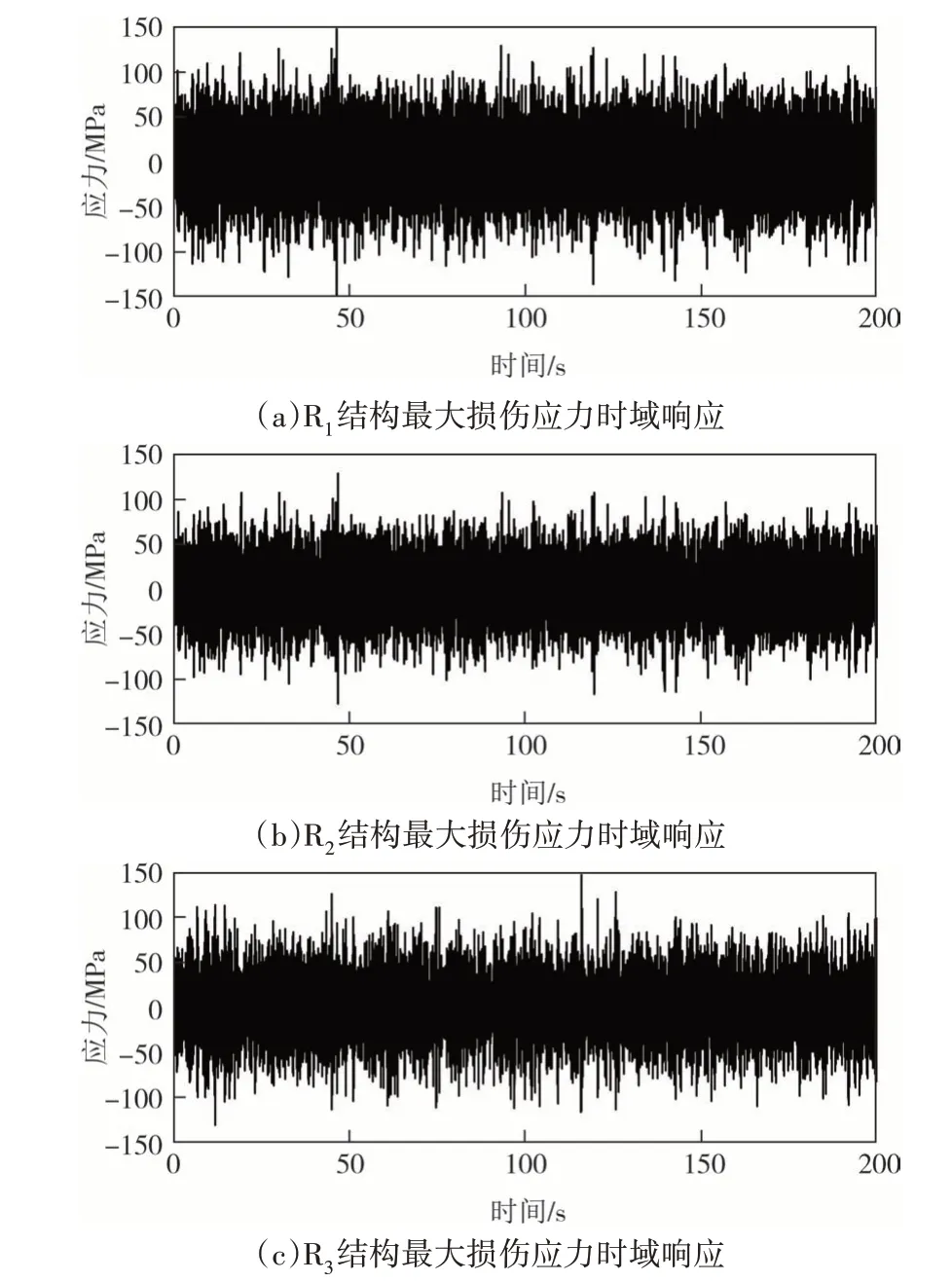
图17 结构最大损伤应力时域响应Fig.17 Time domain response of maximum structural damage stress

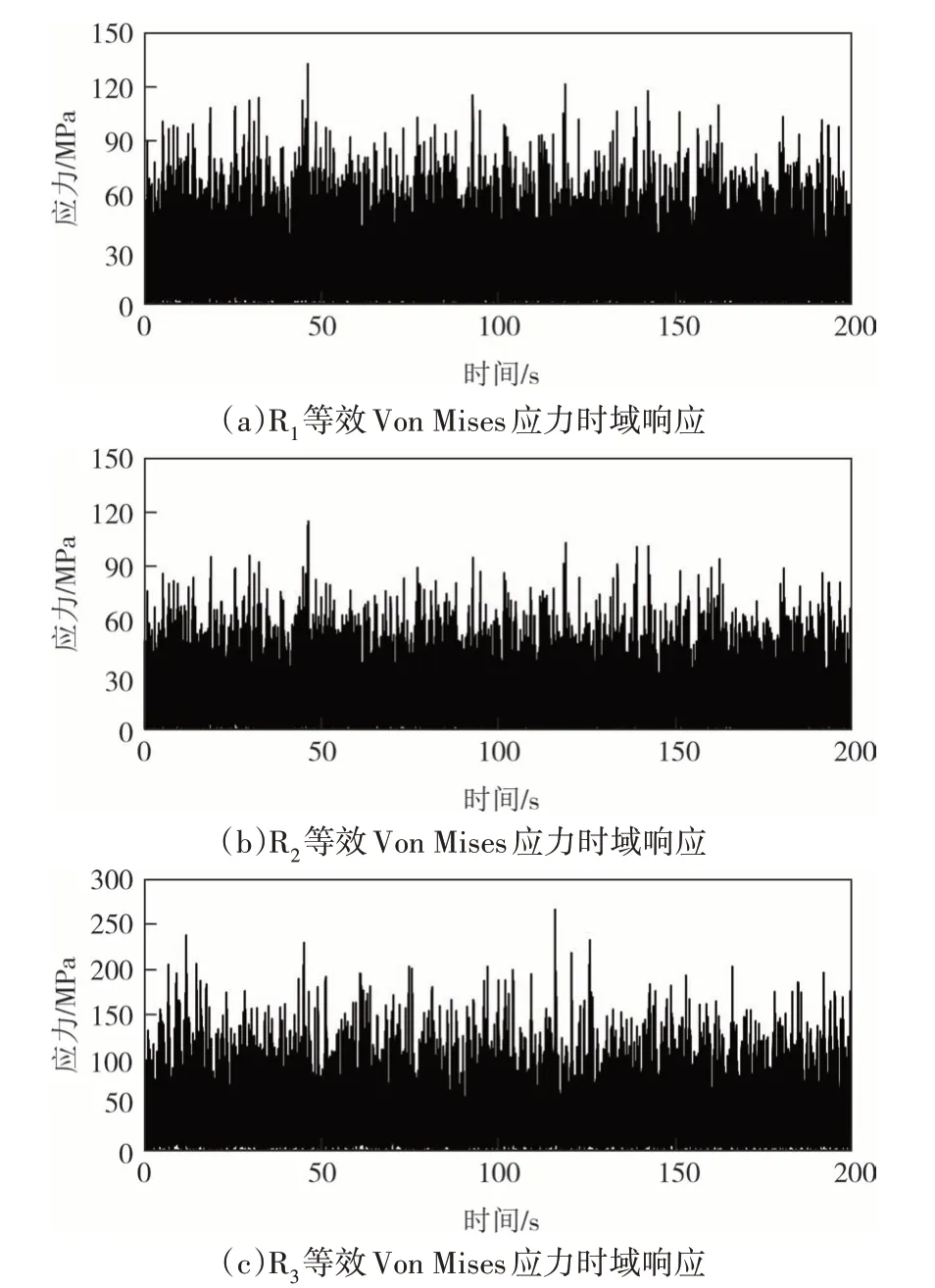
图18 等效Von Mises应力时域响应Fig.18 Time domain response of equivalent Von Mises

式中：σVM为时域等效Von Mises应力.

由表6 电池包的振动应力对比可知，频域法和时域法的RMS 应力值相近，最大相对误差小于15.2%，表明二者所预测的平均动应力相近.

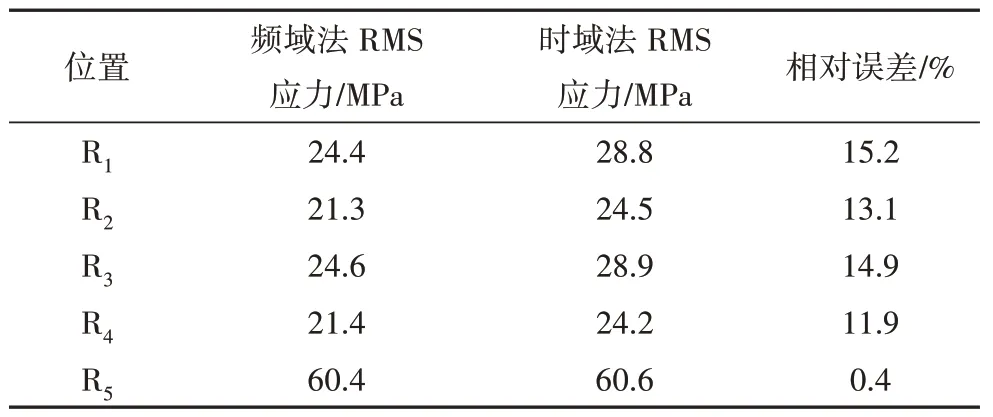
表6 结构振动应力对比Tab.6 Comparison of structural vibration stress

由表7 可知，频域法的“5σ”应力值比“3σ”应力值更接近时域法最大Von Mises 值，最大相对误差小于13.1%.

表7 频域法估算应力峰值与时域法最大Von MisesTab.7 Stress peak of frequency domain method and maximum Von Mises of time domain method

4.3 疲劳寿命

基于应力响应，利用频域法和时域法对图15 和图16 所示危险位置的疲劳寿命进行预测，并用 式（13）计算二者之间的误差因子，结果见表8.

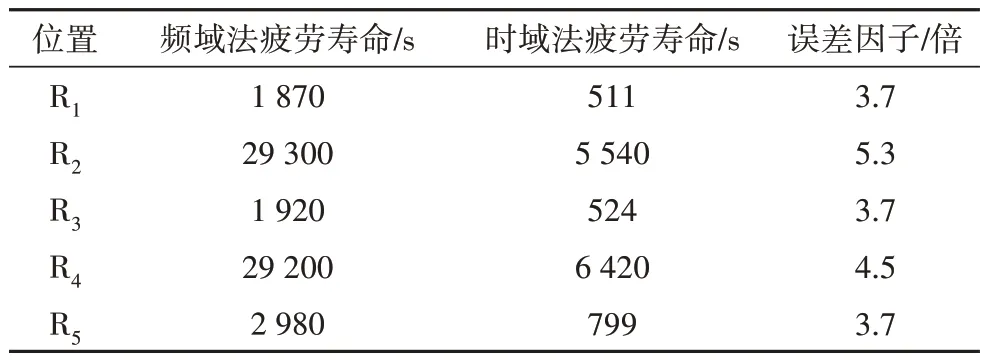
表8 振动疲劳寿命Tab.8 The vibration fatigue life

式中：Nfreq为频域法计算疲劳寿命；Ntest为时域法计算疲劳寿命.

由表8 可知，频域法计算的疲劳寿命为时域法计算值的3.7～5.3 倍，主要原因是Dirlik 模型和应力响应PSD谱差异的影响.

1）Dirlik 模型的影响.由雨流计数和Dirlik 模型得到的R2位置应力幅循环次数曲线的对比可知，时域法和频域法在同一应力幅值处计算的循环次数存在一定差距，如图19 所示.由表9 可知，Dirlik 模型造成的差距在1.2～1.5倍，误差影响率的范围为23%～41%，平均影响率为34%.

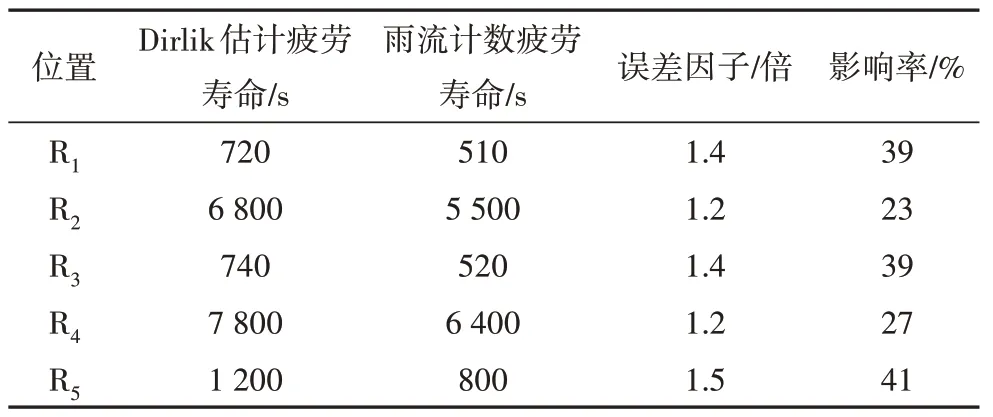
表9 Dirlik模型的影响Tab.9 Influence of Dirlik model approach

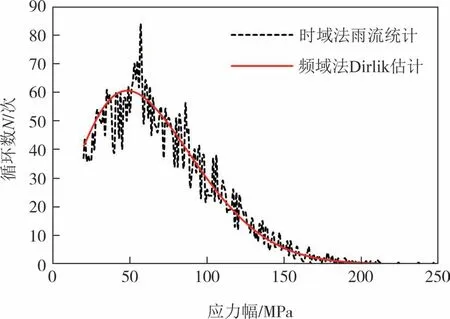
图19 雨流计数与Dirlik模型的应力循环次数对比Fig.19 Comparison of stress cycles between rain-flow counting method and Dirlik model

2）应力响应PSD 谱差异的影响.由式（3）可知，时域法的疲劳寿命计算基于临界面正应力的雨流计数，而频域法疲劳寿命计算基于Von Mises 等效应力PSD谱，其计算表达式为：

式中：Gσσ(fm)为应力响应PSD 矩阵；A为Von Mises的二次计算式.

临界面正应力与Von Mises 等效应力的差异是导致时域法和频域法计算的应力响应PSD 谱出现差异的主要原因，如图20所示.

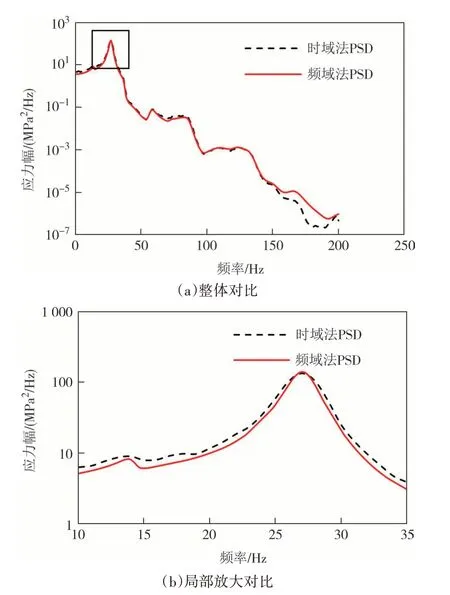
图20 R2应力响应PSD谱对比Fig.20 Comparison of stress response PSD at R2

应力响应PSD 谱的差异通过应力循环次数影响结构疲劳寿命的计算值，如图21所示.由表10可知，应力响应PSD 谱差异导致的误差因子在2.5～4.3倍，误差影响率的范围为59%～77%，平均影响率为66%.

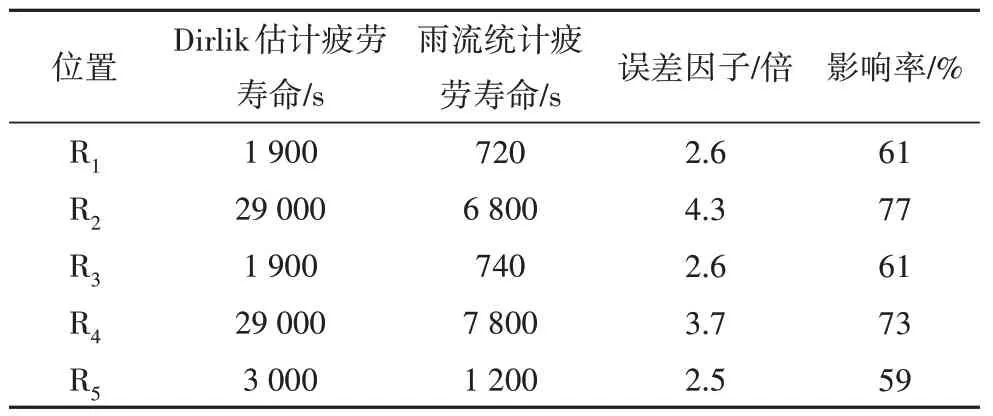
表10 应力PSD谱差异的影响Tab.10 Influence of stress PSD difference

图21 应力PSD谱差异的影响Fig.21 Influence of stress PSD difference

4.4 计算效率和精度

4.4.1 计算效率分析

时域响应信号的采样频率是影响时域法分析精度的重要因素，为了保证时域响应信号在关心频率带宽内无混叠和不失真，根据Shannon 采样定理，采样频率至少为关心信号最高频率的2倍［20］.

由表2 可知，电池包的最高分析频率为200 Hz，因此时域法最低采样频率应为400 Hz，采样时间间隔为0.002 5 s，完成一次总时长为200 s 的分析至少需要80 000 个迭代步，而在同样频率分辨率的情况下，频域法只需要595 个迭代步，计算效率比时域法高了约134倍.

4.4.2 计算精度验证

为了验证时域法和频域法的计算精度，基于表2加速度PSD 谱，利用LDS 振动台对电池包进行12 h随机振动测试，如图22 所示.试验结果显示，R2位置处的最低振动疲劳寿命为12 h目标寿命的16.4%，见图23.

图22 电池包随机振动疲劳测试Fig.22 The random vibration fatigue test of battery pack

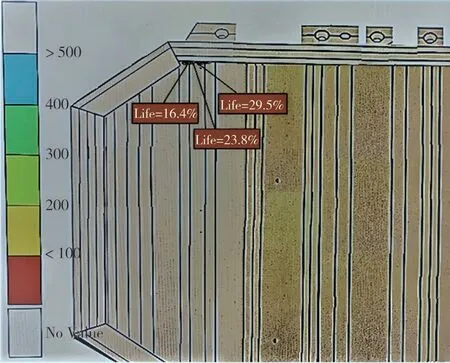
图23 R2疲劳测试寿命Fig.23 The test fatigue life of R2

由表8可知，频域法R2疲劳寿命为29 300 s，占12 h目标寿命的67.8%，而时域法疲劳寿命为5 540 s，占12 h 目标疲劳寿命的12.8%，与试验测试结果更接近，计算精度更高.

5 结论

1）频域法和时域法在电池包振动总级、应力RMS 值以及疲劳寿命预测趋势上相近，但与复杂的时域临界面法相比，频域法计算效率更高，约高134倍.

2）考虑到频域法“3σ”计算值与时域法最大幅值的差距较大，推荐频域法采用“4σ”或“5σ”原则对加速度和应力的最大幅值进行估算.

3）Dirlik 模型和应力响应PSD 谱的差异是造成频域法和时域法的疲劳寿命值产生较大差距的主要原因，其中Dirlik模型造成的差距小于1.5倍，平均影响率约为34%.

4）与频域法相比，时域法计算精度更高，因此为了对电池包结构振动的疲劳性能进行更快和更精确的验证，可先利用频域法对结构振动疲劳危险位置进行快速预测，再利用时域法对危险位置的疲劳寿命进行精确计算.