基于振动速度与噪音的横梁动态特性优化

叶寒 ，高艺 ，刘军 ，张军 ，李莉 ，刘旭波 ，李诗晨 ，董高翔 ，姜乐付 ，郭俊辉 ，刘华

（1.南昌大学 先进制造学院，江西 南昌 330009；2.江西省佳时特数控有限公司，江西 南昌 330052）

近年来，随着全球化与制造业的快速发展，加工零部件对高精密机床的加工精度与静动态特性的要求越来越高［1］.横梁作为高精密机床的关键零部件之一，其结构设计的合理与否，很大程度上影响着机床整机的加工精度［2-4］.

国内外学者对机床关键零部件的静动态特性进行了许多研究，如张伟华等［5］、邱自学等［6］以及刘政等［7］，优化了机床的床身、滑枕以及立柱等关键零部件.Mahendrakumar 等［8］对机床床身进行形状优化.Venugopal 等［9］设计了新型的机床底座.Xiao 等［10］对特定机床进行了轻量化设计.Ahmadi 等［11］将激振实验与仿真结果进行比对.Xu 等［12］通过模态应变能识别了某车床刚度薄弱位置.Yeh 等［13］、Min 等［14］、Diaz等［15］把固有频率当作状态变量来进行相关零件的优化.

本文以某型小五轴高精密数控机床的横梁为研究对象，对其动态特性进行分析与验证，最后根据试验结果与有限元仿真对其进行优化.

1 结构动态特性计算理论

在评估横梁动态性能时，固有频率是一个很关键的因素.根据机械振动相关的理论知识，当结构受到的外部激励与横梁固有频率相同或接近时，横梁会产生比较大的振动，影响加工精度［16］.获得固有频率的方法有计算模态分析和试验模态分析［17］.计算模态可以把任一连续结构近似地看作是无限多个微刚体组成的，每个微刚体有6 个自由度，由此可推得这一结构有无限个自由度.自由度数是决定结构性质矩阵维数的重要因素，因此也是决定固有频率数量的重要因素［18-19］.测量实验模态时的测点选择与布置有着客观条件的限制，如测量条件、测量工况以及有限的频率范围等，测试系统如加速度传感器和数据采集动态频率等，都限制了可测的模态阶数，因此实验模态的测点选择有一定的任意性［20］.计算模态本质上是对所研究的结构进行振动方程的求解，求得的特征值即是所研究结构的固有频率.

不考虑阻尼的情况下，所研究结构的振动方程为：

式中：M为系统的质量矩阵；K为系统的刚度矩阵；t为时间，为系统的加速度列向量；为系统的速度列向量.

对以上方程设一个特解：

式中：X（t）为系统的位移列向量；ϕ为位移幅值矩阵；j为复数；ω为系统模态频率；ejωt代表振动形状.

将特解代入式（1）可得

系统的模态频率ω可从矩阵的行列式中得到.

实验模态则通过测量结构的输入和输出，由输入输出计算结构频率响应函数（Frequency Response Function，FRF），不测量结构的质量和刚度.

频响函数的分母包含系统极点信息，也就是所研究结构的固有频率信息.理论上，从频响函数中，可以得到所研究结构的全部模态信息.频响函数为：

式中：δ1为上残余项；δ1为下残余项；Qr为系统输出响应位置；Ψr为系统输入响应位置；λr为系统极点.

式（4）分子部分的改变依赖于输入与输出，但是所研究结构的极点不变.这说明仅一个测量点就可以测得所研究结构的固有频率.

从理论角度上讲，计算模态采用的方法是对基本特征方程进行特征值求解，获得特征值（也就是模态频率）；而实验模态是通过输入输出点和频响函数得到模态频率.实验模态是对所分析的实际结构进行测量，只要不把测点设置在节点上，分析得到的模态参数是非常精确的；而计算模态会对结构的三维模型进行合理简化.

本文以某型小五轴高精密数控机床横梁为研究对象，以提高横梁动态性能为目标进行优化设计.通过理论分析和实验验证相结合，优化了有限元分析横梁设计的薄弱部位，以改善横梁的静动态性能.

2 横梁的三维模型及计算模态

本文所研究的某型小五轴高精密数控机床，设计的主要目的是加工各种高精度零件，而由于横梁设计不当，过度追求轻量化，导致动态性能不足，机床加工精度不满足要求.机床实物如图1 所示，装配图如图2 所示，机床横梁的铸件模型如图3 所示，横梁的三维数字模型如图4所示.

图1 机床实物图Fig.1 The physical machine tool

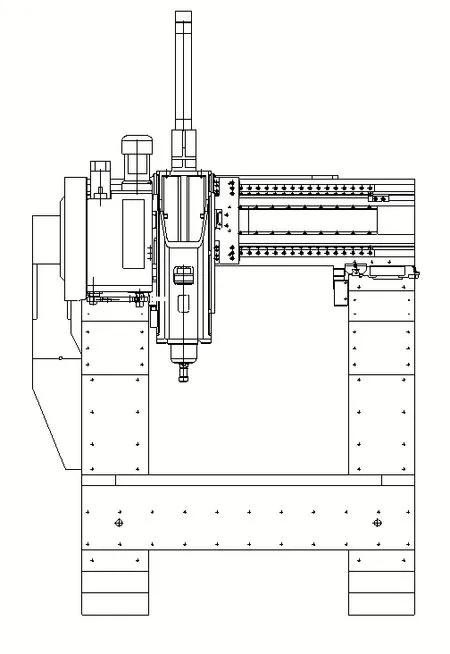
图2 机床装配图Fig.2 Machine tool assembly drawings

图3 横梁铸件模型Fig.3 Beam casting model

图4 横梁三维数字模型Fig.4 3D digital model of the beam

在有限元分析软件中计算所研究横梁的固有频率，设置横梁材料为HT250，弹性模量E=1.175× 105MPa，泊松比μ=0.27，密度ρ=7.8×103kg/m3［21］，进行横梁在装配约束下的计算仿真.

由振动相关理论得，所研究横梁的动态特性主要受前面几阶固有频率的影响［22］.而外界给横梁的激励频率一般不是很高，所以为了避免所研究横梁产生共振或是较大的振动，一般对横梁的前六阶固有频率进行研究.本文所研究横梁的前六阶频率如表1所示.

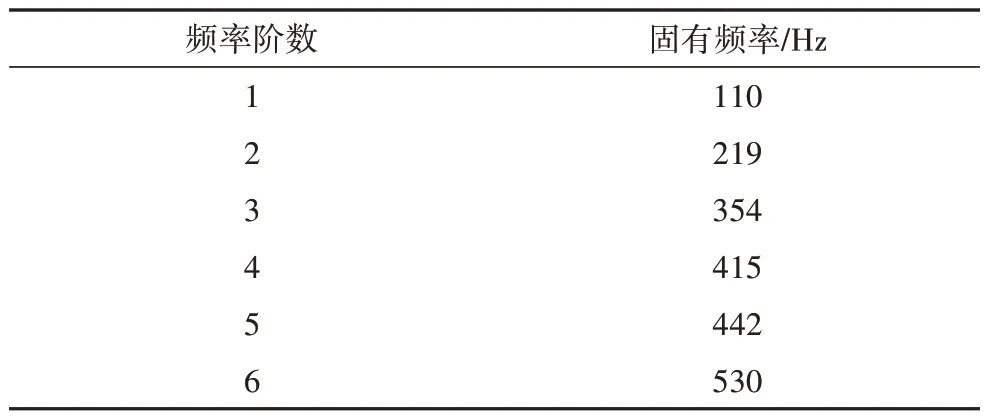
表1 横梁的前六阶固有频率Tab.1 The first six natural frequencies of the beam

3 横梁的实验模态

由于计算模态结果的精度受模型简化程度、网格质量、边界条件加载的准确性以及有限元算法等因素的影响［23］，为了验证计算模态的准确性，对该横梁进行模态实验.

使用印制电路板（Printed Circuit Board，PCB）力锤对装配在机床上的的横梁进行激励.锤头内置的力传感器和安装在横梁上的加速度传感器同步记录下瞬态激励和被测对象的响应［24］.经学习管理系统（Learning Management System，LMS）信号分析仪采集处理数据后传输到计算机，对数据进行模态分析，获取被测对象的模态频率.

整个测试过程包含被测对象横梁、PCB 力锤、LMS 信号分析仪等，试验流程如图5 所示，试验原理如图6所示，试验现场如图7所示.

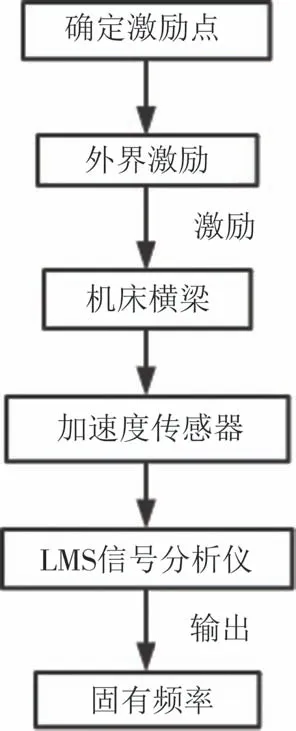
图5 试验流程Fig.5 Trial process

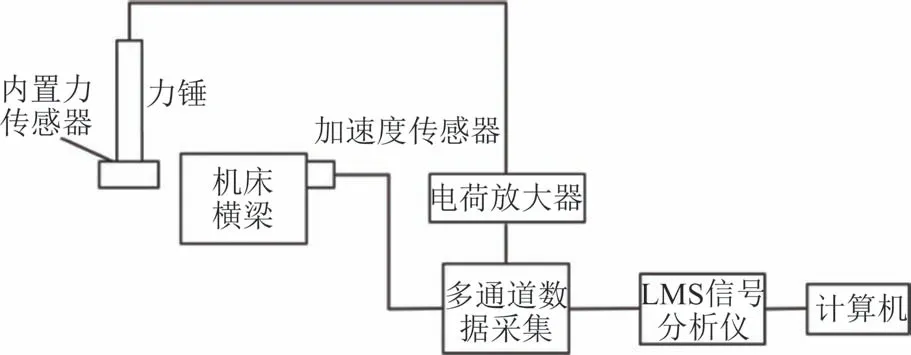
图6 试验原理Fig.6 Test principle

图7 试验现场Fig.7 Test site

进行相应的测试后，得到了5 组实验数据，如表2所示.

表2 横梁的测试频率Tab.2 Test frequency of the beam

横梁固有频率实测与模拟对比如图8 所示.可以看出，试验结果与有限元模拟结果基本拟合.两者之间的最大误差出现在第5阶模态，误差为5.76%.

图8 横梁固有频率实测与模拟对比Fig.8 Measured and simulated comparison of the natural frequency of the beam

4 横梁的外部激励测试

机床主轴是挂在横梁上的，当主轴转动时，作为横梁的激励源之一，会引起横梁振动.如果在某个转速下，主轴出现振动速度和振动噪音突然增大的情况，可能是在此转速下发生了横梁振动.表3 是对主轴进行振动检测的实验数据.在此次实验中，主轴拉力为（6 800±500）N，顶刀量为（0.5±0.1）mm，轴芯窜动为（0.10±0.05）mm，在检测相关参数之前主轴需先跑合，7 000 r/min 跑合30 min，10 000 r/min 跑合15 min，30 000 r/min跑合10 min，主轴变热但不烫手，如主轴很热，需停止运转，跑合结束后再进行测试.

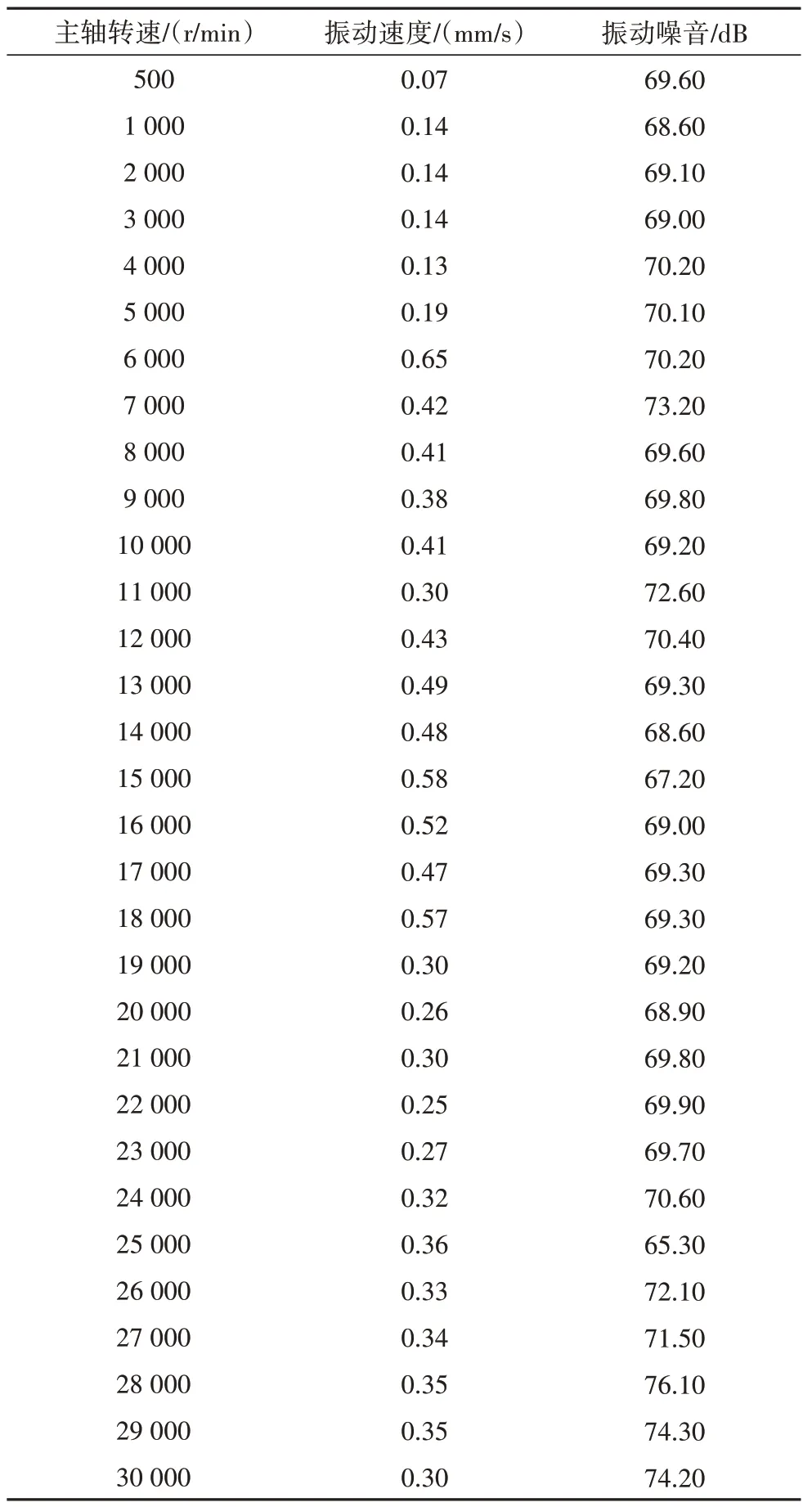
表3 主轴检测数据Tab.3 Spindle inspection data

振动速度和振动噪音之间可能存在相关性，因为它们的相关系数并不为零.根据数据计算出两者的相关系数约为0.43，这表明它们之间存在一定的正相关关系.换句话说，当振动速度增加时，振动噪音也有可能会随之增加.

对表3 数据绘制散点图，分析振动速度与振动噪音与主轴转速的关系，并对所得散点图进行九项式曲线拟合.

拟合方程通用形式如下：

式中：ai为x的i次方的常数项.

拟合后，转速与振动速度和振动噪音的关系如图9、图10所示.

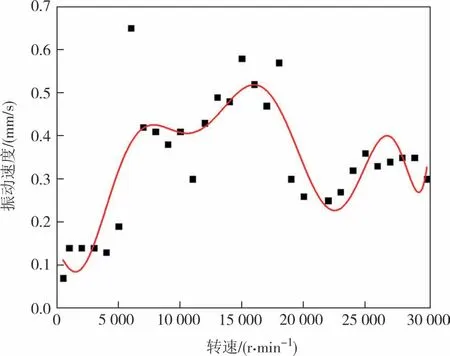
图9 转速与振动速度关系Fig.9 The relationship between rotational speed and vibration velocity

图10 转速与振动噪音关系Fig.10 The relationship between rotational speed and vibration noise

对于转速与振动速度之间的关系，图9 表明随着转速的增加，振动速度也随之增加，但是呈现出一定的非线性趋势，这意味着当转速增加到一定程度后，振动速度增加的速率会减缓，其本身甚至会下降.对于转速与振动噪音之间的关系，图10 表明随着转速的增加，振动噪音的趋势不太清晰.有些点呈现出振动噪音随着转速增加而增大的趋势，但是其他点则表明随着转速的增加，振动噪音反而减小.

这可能是由于所研究机床的主轴在一定转速下的振动会导致横梁产生共振，从而影响主轴的振动速度与噪音.

对两者进行赋权处理，根据振动速度占比为0.5，噪音占比为0.5 的权重分配，建立振动评价指标方程.

式中：xi为第i个转速下的振动速度；yi为第i个转速下的振动噪音；zi为第i个转速下的振动评价指标.

计算得振动评价指标的转置矩阵为：

［0.019 905 074 0.023 049 311 0.023 168 014 0.023 144 274 0.022 946 069 0.025 820 879 0.048 066 841 0.037 667 947 0.036 330 195 0.034 928 401 0.036 235 233 0.031 728 402 0.037 486 303 0.040 123 708 0.039 474 432 0.043 972 982 0.041 501 762 0.039 157 524 0.043 988 442 0.030 921 223 0.028 917 634 0.028 671 948 0.029 590 651 0.032 219 775 0.032 893 892 0.033 058 975 0.033 399 623 0.034 974 781 0.034 547 451 0.032 108 251］

由以上数据可以看出，主轴转速在6 000 r/min 时，振动评价指标最大，因此选取5 000～7 000 r/min的转速作为主轴振动反常范围.在此转速范围下，主轴给横梁的外部频率激励为83～117 Hz.在这个频率范围下，横梁可能产生了较大的振动.而实验测量的横梁一阶固有频率为115 Hz，在83～117 Hz 频率范围内.

因此在后续横梁的优化中，需要提高一阶固有频率，使一阶固有频率远离83～117 Hz的频率范围.

5 横梁的优化

提高所研究横梁的一阶固有频率可以有效改善动态特性，这是提升整机精度的有效措施［25］.如果想要提升一阶固有频率，就需要合理增加横梁质量.该小五轴高精密数控机床在设计横梁时，一味追求轻量化，导致横梁刚性不足，根据工程师建议，需对横梁进行形状优化.在有限元软件中，对横梁仅受自重的情况进行了分析，如图11 所示.为避免计算时间过长，对横梁的数字模型进行简化，忽略了某些非必要特征［26］，如倒角与圆角等.

图11 横梁在自重下变形云图Fig.11 The relationship between rotational speed and vibration noise

由图11 可以看出，横梁仅在自重情况下，最大变形量就有5.504 3 µm，说明横梁抵抗变形的能力不足，刚性不够，设计不合理.经分析可知，横梁的各处壁厚过小，底面顶面以及斜面开槽过大等，需要对这些地方进行形状优化.

原横梁顶面、正面以及前端面壁厚为20 mm，斜面壁厚为15 mm，顶面开槽长度为171 mm，底面开槽长度为380 mm，斜面开槽长度为314 mm、宽度为197 mm 与312 mm.对原横梁进行形状优化后，改进后横梁顶面、正面、前端以及斜面面壁厚为40 mm，顶面开槽长度为140 mm，底面开槽长度为300 mm，斜面开槽长度为240 mm、宽度为149 mm与300 mm.

对改进后横梁仅受自重的情况进行分析，如图12所示.

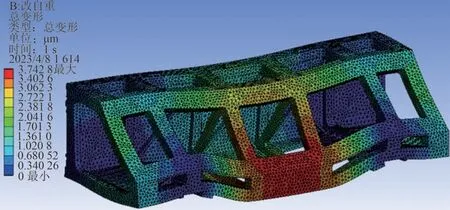
图12 改进后的横梁在自重下变形云图Fig.12 Improved beam deforms cloud under its own gravity

由图12 可以看出，改进后的横梁仅在自重情况下，最大变形量降为3.742 8 µm，下降了约32%，刚性得到一定提升，质量也合理增大.在有限元软件中计算改进后横梁的一阶固有频率为139 Hz，远离了83～117 Hz 的频率范围，相较于原有的固有频率，增加了约20.870%.

6 结论

本文以某型小五轴高精密数控机床横梁为研究对象，以提高横梁动态性能为目标进行优化设计.首先对所研究横梁数字模型进行合理简化，求解横梁的固有频率，然后采用锤击法进行固有频率的实际测量，并把两者进行比对.然后测量主轴在不同转速下振动速度和振动噪音，通过赋权处理，建立振动评价指标方程，得到优化目标，最后对所研究横梁进行形状优化，研究结论如下.

1）实验结果与有限元仿真结果差别不大，曲线基本拟合.两者之间的最大误差出现在第5 阶模态，误差为5.76%.

2）选取5 000～7 000 r/min 的转速范围，作为主轴振动反常范围.在此转速范围下，主轴给横梁的外部频率激励为83～117 Hz.在这个频率范围下，横梁可能产生了较大的振动.而实验测量的横梁一阶固有频率为115 Hz，在83～117 Hz频率范围内.

3）改进后的横梁仅在自重情况下，最大变形量降为3.742 8 µm，下降了约32%，刚性得到一定提升，质量也合理增大.通过有限元模拟得出改进后横梁的一阶固有频率为139 Hz，远离了83～117 Hz的频率范围，相较于原有的固有频率，增加了约20.870%.

本文的研究过程对高精密机床关键零部件的动态特性优化有一定的指导意义.