侧喷射流的仿生鱼表面减阻优化研究
2024-03-25刘国勇宋中鑫朱冬梅
刘国勇 ,宋中鑫,朱冬梅
(北京科技大学 机械工程学院,北京 10083)
覆盖着地球71%面积的海洋蕴藏着丰富的鱼类、矿产、能源等资源[1],对于海洋的开发和争夺成了很多发达国家的战略重点.仿鱼形水下机器人是一种集机械、智能控制于一体的高科技设备,在民用、军事等科学研究领域均体现出了广阔的应用前景和巨大的潜在价值[2].国内外学者越来越重视仿生机器鱼的研究与开发,并取得了很多阶段性成果.
在基础理论方面,Gray[3]认为海豚的肌肉所能提供的功率只相当于与它身体相似的刚体模型以15~20节的时速前进时所需功率的1/7,他从能量守恒的角度提出了一个结论:海豚的游动效率远远超出了100%.人们将这个结论推广到整个鱼类,称为“Gray 悖论”.直到今天,这个悖论还激励着广大科学工作者以精确的科学方式证明其对错.Lighthill[4]将空气动力学的二维机翼理论运用于尾鳍推进的研究,提出了用于分析鲹科鱼类推进模式的“细长体理论”,后进一步又提出了“大摆幅细长体理论”[5].Wu[6]通过研究提出了“二维薄板理论”,将鱼看成一个具有弹性的薄板,进一步又提出了“非定常二维波动板理论”[7],该理论分析了扁平月牙尾鱼的推进及优化方式.在应用研究方面,Triantafyllou 等[8]开发并研制出了名为RoboTuna 的机器鱼,它是世界上第一台真正意义上的仿生机器鱼,能通过摆动尾柄和尾鳍像鱼一样在水中游动,最高游动速度可以达到 2 m/s.Wang等[9]设计开发了各种类型的机器鱼,并将刚体动力学与Lighthill的大幅度细长体理论相结合,提出了由尾鳍驱动的机器人鱼的完整动态模型.国内对仿生鱼的研究起步较晚,中国科学院自动化研究所研发的多连杆仿生海豚,可实现偏航与俯仰的运动,且首次在水下机器人上实现了混合杂技特技[10].张艺博等[11]以鳄鱼为原型设计了一种可实现水陆两栖运动的仿生机器人,弥补了国内外的水下机器人机动性能差、复杂地形适应性弱等缺陷.
在减阻方面,仿生减阻、微气泡减阻、超空泡减阻等各种减阻技术相继被提出并应用于实践中,取得了很好的经济效益,具有很好的科研和应用价值[12].仿生射流减阻技术是一个新兴的研究领域,国内外研究者们对侧向射流和逆向射流技术进行了一系列相关的研究[13-14],发现均有很好的减阻效果.赵刚等[15]基于鱼类鳃裂部位仿生射流表面理论分析,对仿生射流表面回转体进行射流试验,发现仿生射流表面具有较好的减阻效果,最大减阻率达到10.8%.李芳等[16-17]对流体在多孔仿生射流表面上的流动特性进行了数值模拟,发现减阻效果随着流速比的增大而增强,最大减阻率为59.02%,并解释了射流表面减小摩擦阻力的原因及对近壁区边界层的控制行为.
在仿生鱼领域,现有的研究主要针对仿生鱼的控制、驱动、力学特性等方面进行研究,对表面减阻的研究相对比较少.此外,当前关于水下表面减阻的研究,主要是基于平板模型或圆筒模型开展,对于流场环境复杂的曲面模型研究较少.本文依据金枪鱼的外形建立仿生鱼模型,将模型与射流减阻技术相结合,研究射流孔的形状、高度、位置、高宽比对仿生鱼表面减阻的影响,并采用响应面法分析不同因素相互作用时对减阻性能的影响,得出最优减阻方案,对仿生减阻有一定参考意义.
1 模型建立
1.1 模型基本参数
1.1.1 仿生鱼模型基本参数
金枪鱼适合高速游动,可长时间以30~50 km/h(8.3~13.9 m/s)的速度巡游,瞬间速度最高可达150 km/h,在仿生领域备受关注.本文以金枪鱼为仿生对象建立光滑模型,巡游速度范围取8~14 m/s,使用解析式流线型模仿金枪鱼的外形轮廓,忽略金枪鱼的鱼鳍,仿生鱼的几何参数如图1 所示.其中L为鱼体长度,LE为进流段长度,LR为去流段长度,D为最大截面直径,DT为尾端截面直径.本文主要研究射流孔的结构参数对仿生鱼模型的减阻影响,定义仿生鱼模型的尺寸参数为:L=100 mm,LE=30 mm,LR=70 mm,D=30 mm,DT=3 mm.

图1 仿生鱼的几何参数示意图Fig.1 Schematic diagram of the geometric parameters of the bionic fish
1.1.2 射流孔基本参数
设计了前月牙形、后月牙形、前三角形、后三角形4种不同形状的射流孔,如图2所示.其中s为射流孔宽度,h为射流孔高度.射流孔来源于对鲨鱼鳃部的仿生模拟,通过观察鲨鱼腮部大小,其高度介于形体最大直径的1/6 至1/3,本文研究的射流孔高度为6~10 mm,高宽比ks=h/s,范围定为4~10.

图2 4种形状的射流孔Fig.2 Four types of jet holes
将射流孔垂直于来流速度方向布置在模型上,如图3 所示.射流孔到鱼首的距离定义为射流孔位置x,本文研究的射流孔位置为5~25 mm.

图3 射流孔的布置示意图Fig.3 Schematic diagram of the jet hole arrangement
射流表面减阻率η的计算式为:
式中:FS为光滑表面所受黏性阻力;FJ为射流表面所受黏性阻力.定义相对射流流量Vs:高8 mm 的后三角形射流孔,在射流速度为1 m/s 时,单位时间内的射流流量为V*,相同时间内在任意射流速度下的射流流量为V,则V/V*为该工况下的相对射流流量Vs.从而可以进一步定义单位体积射流减阻率ηs:
式中:ηs为射流表面减阻率η与相对射流流量Vs的比值,表示单位体积流量的射流对减阻率的贡献.在射流孔大小、射流孔形状或射流速度不同时,以ηs来比较不同工况下的射流减阻的效率,作为评价射流减阻性能的一个重要指标.
1.2 网格划分
本文研究的是仿生鱼绕流问题,设置大小为Φ400 mm×400 mm 的计算域,为减小工作量,建立 1/2 三维模型.在仿生鱼距离鱼首5 mm 处,添加高度h=8 mm,高宽比ks=4,射流孔角度为0°(射流孔垂直鱼体轴线布置)的前月牙形射流孔.由于模型结构较为复杂,难以对其进行结构网格划分,对模型进行Tetra/Mixed 非结构网格划分,并使用Robus(tOctree)划分策略.这种方法在网格划分过程中首先生成模型体网格,在这之后生成模型面网格,对复杂结构模型的网格划分适应能力更强,比较适合用于本节的仿生鱼射流减阻模型.
数值模拟计算结果的准确性与网格的数量和密度有着很大关系,而在关注流体表面压差阻力和摩擦阻力时,需要根据边界层的实际情况设置合适的边界层网格高度.本文研究的仿生鱼绕流问题为湍流问题,在定义边界层网格高度时应使第一层网格的y+<10,以精确求解边界层流场的物理问题,本文取y+=2,在来流速度为14 m/s 时计算得出近壁面第一层网格的高度设置约为0.003 mm,网格高度增长比率设置为1.001,全局网格尺寸设置为10 mm,仿生鱼模型表面的最大网格尺寸设置为0.2 mm,网格总数为400 万,如图4 所示,下文模型的网格划分在此基础上进行.其中,网格划分使用ICEM 15.0,仿真计算在Fluent 15.0中进行.
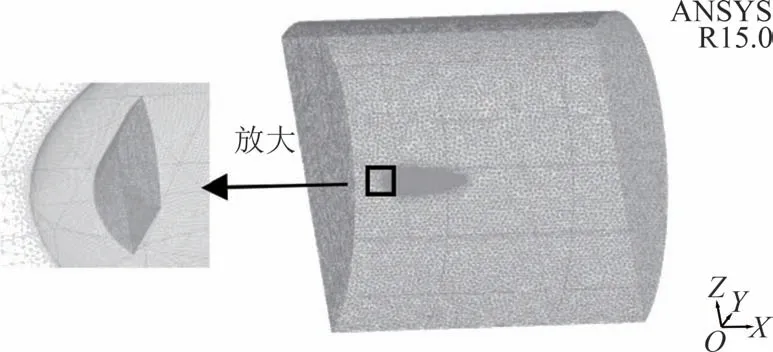
图4 射流模型的网格划分Fig.4 Grid division of jet model
Quality 是CFD 常用的网格质量评估标准之一,对于不同类型的网格其采用不同的衡量方式,对于三角形或四面体网格,其代表着计算高度与每一条边的长度比值.其表示网格的整体质量,数值为0~1,数值为1时最好,通常认为0.3以上时网格质量较好.图5 为三维模型网格质量,从图5 中可以看出,网格的Quality大部分处于0.38以上,网格质量较好,满足计算要求.
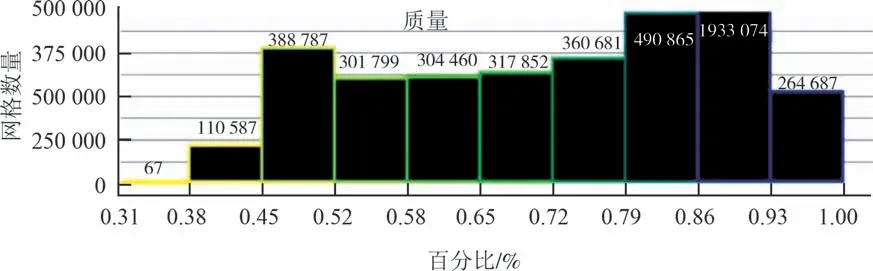
图5 三维模型网格质量Fig.5 3D model mesh quality
1.3 边界条件设置
本文研究主要关注仿生鱼表面阻力,其中摩擦阻力(黏性阻力)与边界层处流体的剪切应力有关,需要精确求解边界层中的黏性底层,因此湍流模型选择SSTκ-ω的模型,使用低雷诺数方程求解.求解器选择基于压力的分离求解器,分离算法选择SLMPLEC 算法,离散格式选择二阶迎风离散格式(Second Order Upwind),收敛精度设置为十万分之一,流场介质设置为液态水、不可压缩流体,密度为998.2 kg/m3,黏度为0.001 003 kg(/m·s),通过计算可得出仿生鱼流场周围雷诺数为8.0e+5~1.4e+6.流场入口为速度入口(Velocity-inlet),出口为压力出口(Pressure-outlet),并将压力出口的表压(Gauge Pressure)设置为默认为0.流场外边界、仿生鱼表面以及旋转壁面设置为无滑移壁面边界条件(Wall).流场入口和出口的湍流黏度比(Turbulent Viscosity Ratio)设置为默认的5%,其余设置保持默认.1/2 模型计算域如图6 所示.下文的模型分析在此基础上进行.
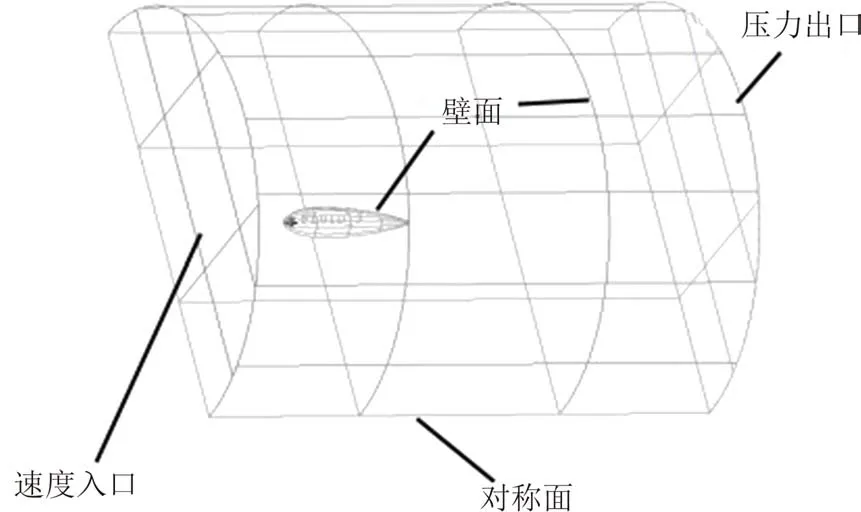
图6 1/2模型计算域Fig.6 Calculation domain of one-half model
1.4 网格无关性验证
仿真计算受到计算机计算能力的限制,因此需要网格独立性检验,来获得合适的网格尺寸和数量,以保证仿真模拟计算的精度和效率.采用3 种方案对仿生鱼模型进行结构网格划分,网格数量分别为200 万、400 万、800 万.保持其他设置相同,分别将网格导入Fluent 中进行计算.3 种方案下计算得出的阻力系数如表1 所示,其中阻力系数变化比为网格数量200 万和400 万时计算得到的结果分别与网格数量为800万时的计算结果相比较得到的.

表1 3种网格数量下的阻力系数计算结果及对比Tab.1 The calculation results and comparison of resistance coefficient under three kinds of grid numbers
由表1 中可以看出,网格数量从400 万增加到800万时,各项阻力变化比在1%以内,表明网格数量为400万的量级能够满足计算精度要求.
2 主流场速度及射流孔结构参数对减阻的影响
2.1 主流场速度对减阻的影响
在仿生鱼距离鱼首5 mm处,添加射流孔高度h=8 mm,形状为前月牙形的射流孔.在主流场速度(来流速度)v=8~14 m/s(间隔1m/s 取值),射流速度VJ=0.2~1.2 m/s(间隔0.2 m/s 取值)的情况下,分析主流场速度v对减阻效果的影响.
图7 为不同主流场速度下总阻力减阻率与速度比VJ/v的关系.从图中可以看出,在射流速度VJ与主流场速度v的比值保持不变的情况下,不同主流场速度下的减阻率比较接近.这说明,合理调整射流速度VJ的大小,在主流场速度较大时也能够获得较高的减阻率.
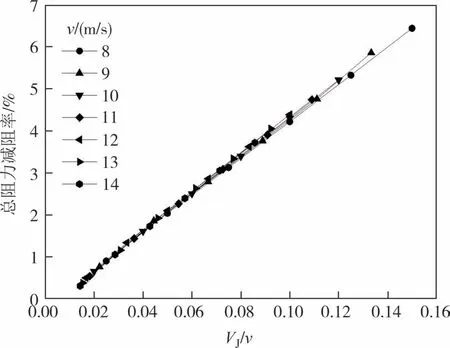
图7 不同主流场速度下减阻率与速度比的关系Fig.7 Relationship between drag reduction rate and velocity ratio under different main flow field velocities
图8 为不同主流场速度下仿生鱼模型的表面单位体积射流减阻率.从图中可以看出,在主流场速度相同时,射流速度VJ越大,仿生鱼模型的表面单位体积射流减阻率越高.在相同射流速度VJ下,主流场速度v越大,单位体积射流减阻率越低.

图8 不同主流场速度下的单位体积射流减阻率Fig.8 Drag reduction rate of unit volume jet under different main flow field velocities
2.2 射流孔结构参数对减阻的影响
在主流场速度v=14 m/s,射流速度VJ=0.2~1.2 m/s(间隔0.2 m/s 取值)的情况下,分别单独改变射流孔形状、射流孔高度、射流孔位置、射流孔高宽比这4个参数,分析其对减阻效果的影响,仿真分析结果如图9所示.
由图9(a)可以看出,随着射流速度VJ的增大,不同形状射流孔的单位体积射流减阻率呈现出先增大后趋于稳定的趋势,在相同射流速度下,后三角形的射流孔减阻效果更好.由图9(b)可以看出,在同一高度下随着射流速度的增大,单位体积射流减阻率逐渐增大,随着射流孔高度h的增加,不同射流速度下的单位体积射流减阻率呈现出先增大后减小的趋势.由于单位体积射流减阻率表示单位体积流量的射流对减阻率的贡献,改变射流孔位置并不会改变单位体积流量,因此选取总阻力减阻率来评价不同射流孔位置的减阻效果,如图9(c)所示.从图中可以看出,在射流孔位置x相同的情况下,减阻率随着射流速度VJ的增加而增大,且射流孔越靠后,总阻力减阻率随射流速度增加而增大的幅度就越小.在射流速度相同的情况下,射流孔越靠前,总阻力减阻率就越大,且射流速度越大,减阻效果越明显.由图9(d)可以看出,当射流孔高宽比ks=4 时,仿生鱼模型的表面单位体积射流减阻率随射流速度的增大而增加,并趋于稳定值;当ks>4 时,仿生鱼模型的表面单位体积射流减阻率随射流速度的增大而减小最终趋于稳定.在射流速度VJ相同的情况下,高宽比ks为6 时单位体积射流减阻率最大.
3 参数优化设计
在传统的设计过程中,往往需要考虑许多参数,而每个参数又需要足够的变量来提供样本数据,这样工作量是随着参数数量的增多指数型增长的,因此往往采用优化设计的技术进行参数优化.本文拟采用响应面法分析射流孔各个结构参数在交互作用时对减阻的影响,并求出最优设计方案.
3.1 实验设计
影响仿生鱼表面减阻的结构参数主要有射流孔形状、射流孔高度、射流孔位置及射流孔高宽比等.根据Box-Behnken 中心组合试验设计原理,本文使用Design-Expert 软件进行三因素三水平试验,射流孔高度、射流孔位置、射流孔高宽比为自变量,仿生鱼模型的总阻力为响应值,其试验水平及仿生鱼的总阻力分别见表2 和表3.确定相关因素不变量为:射流孔形状为后三角形,主流场速度v=14 m/s,射流速度VJ=1.2 m/s.

表2 响应面分析与因素水平表Tab.2 Response surface analysis and factor level table
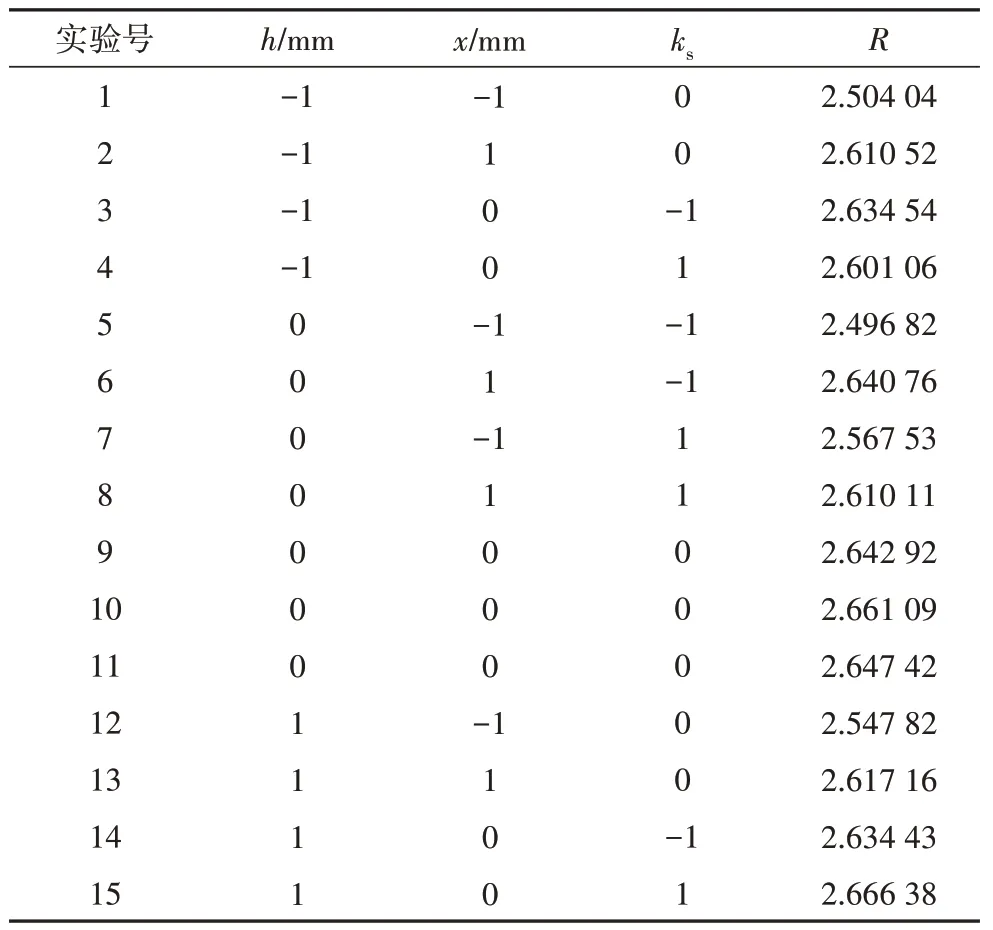
表3 响应面实验设计及结果Tab.3 Response surface experimental design and results
3.2 回归方程建立与分析
将表3 中的数据导入Design Expert 软件中进行多元回归拟合,建立回归方程如下:
式中:R表示模型总阻力的预测值.
对回归方程进行显著性分析,结果如表4所示.
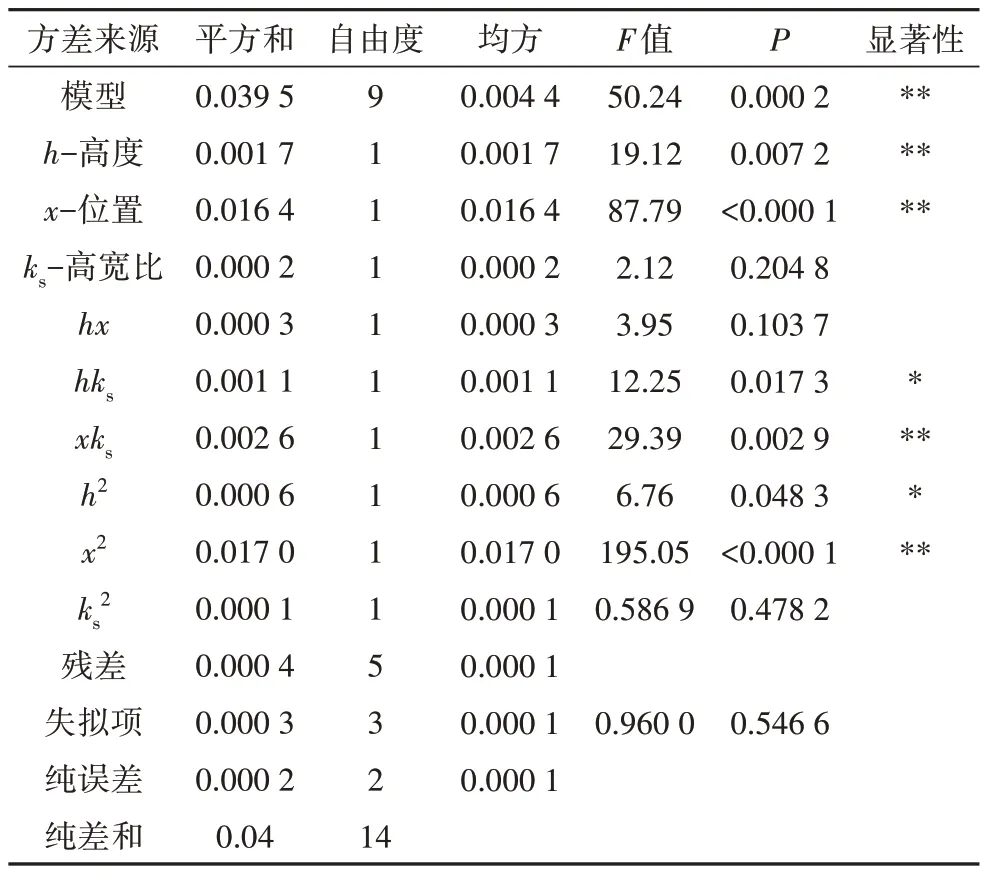
表4 模型总阻力回归方程分析Tab.4 Analysis of the model total resistance regression equation
模型的F值为50.24,P值为0.000 2,表明该模型是显著的,可信度较高.回归方程中的h、x、hks、xks、h2、x2较为显著,其余三项不够显著,但整体来看,该二次回归方程模型比较显著,与实际值能够较好的拟合,可以使用此模型对仿生鱼模型的总阻力大小进行预测.
3.3 响应面分析
分析比较射流孔高度、射流孔位置、射流孔高宽比3个参数对总阻力的影响,使一参数固定不变,比较其余两参数对总阻力的影响,结果如图10~图12所示.

图10 射流孔高度与射流孔位置对仿生鱼总阻力影响Fig.10 Effect of jet hole height and jet hole position on total drag of bionic fish
等高线的形状能够反映交互效应的情况,椭圆形表示交互程度强,圆形表示交互效应弱.
由图10 可以看出,在射流孔的高宽比固定时,高度h和位置x交互作用等高线图呈现椭圆形,表明二者的交互作用显著.由图10(a)可知,仿生鱼的总阻力随着高度h和位置x的增加,呈现出先上升后下降的趋势,且位置x的上升幅度大于高度h,说明射流孔位置对总阻力的影响较大.当射流孔高度为 10 mm,射流孔位置为5 mm时,模型预测的仿生鱼总阻力达到最小值2.547 82 N.当射流孔高度固定时,位置x与高宽比ks对总阻力的影响如图11 所示.由图11(a)可知,随着位置x和高宽比ks的增大,总阻力呈现出先上升后下降的趋势,且位置x的上升幅度大于高宽比ks,说明射流孔位置对总阻力的影响大于射流孔高宽比.由图11(b)可知,射流孔位置x与射流孔高宽比ks的交互作用显著.当射流孔位置为 5 mm,射流孔高宽比为4 时,模型预测的仿生鱼总阻力达到最小值2.496 82 N.如图12 所示,由图12(a)可知,随着高度h和高宽比ks增加,总阻力呈现出先上升后下降的趋势,但这一趋势并不明显,高度h的上升幅度相对而言要大于高宽比ks,说明射流孔高度对总阻力的影响大于射流孔高宽比.当高度为6 mm,高宽比为10 时,模型预测的总阻力达到最小值2.601 06 N.

图11 射流孔位置与射流孔高宽比对仿生鱼总阻力影响Fig.11 Effect of the position of jet hole and the ratio of height and width of jet hole on the total drag of bionic fish
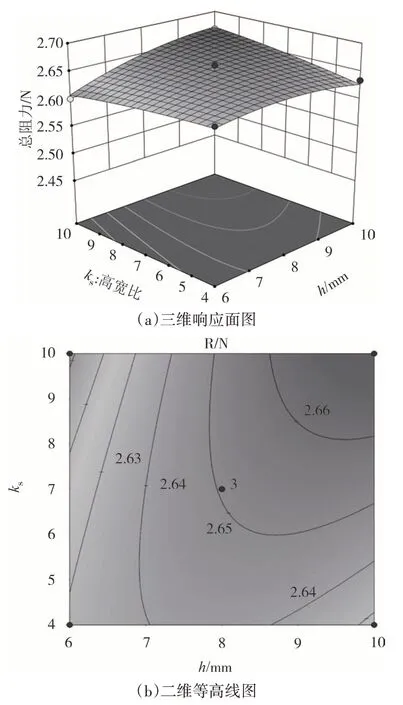
图12 射流孔高度与射流孔高宽比对仿生鱼总阻力影响Fig.12 Effect of jet hole height and jet hole ratio on total drag of bionic fish
利用Design-Expert软件分析优化,通过系统爬坡模拟寻优法,以总阻力最小为目标得到的最优方案为:射流孔高度为6 mm、射流孔位置为5 mm、射流孔高宽比约为4,此时模型预测可达到的仿生鱼总阻力最小值为2.483 46 N.采用优化后的方案,进行仿真验证,重复3 次,取其平均值得到的仿生鱼总阻力为2.510 21 N,对应的减阻率为6.49%.
4 结论
本文以金枪鱼为仿生对象,建立了仿生鱼的光滑形体模型和添加射流孔的模型,采用数值模拟的方法,分析了主流场速度、射流孔结构参数等因素发生改变时对仿生鱼表面阻力产生的影响.使用响应面法分析了不同射流孔结构参数在共同作用时对仿生鱼表面减阻的影响,得出了最优减阻方案.
得出的主要结论如下:
1)当来流速度增加时,需要增大射流速度,使得射流速度与来流速度的比值较大,才能获得较高的减阻率.
2)在相同射流速度下,后三角形的射流孔减阻效果更好;随着射流孔高度h的增加,不同射流速度下的单位体积射流减阻率呈现出先增大后减小的趋势;在所给的范围内,射流孔越靠前,总阻力减阻率就越高,且射流速度越大,减阻效果越明显;当高宽比ks为4时,单位体积射流减阻率随射流速度的增大而增加,当ks>4 时,单位体积射流减阻率随射流速度的增大而减小最终趋于稳定.
3)在射流孔形状选用后三角形、射流孔高度为6 mm、射流孔位置为5 mm、高宽比为4 时,能够达到更好的减阻效果,通过仿真验证得到了6.49%的减阻速率.
