基于等效单自由度的涡轮扫频振动研究
2024-03-23张虹张一帆王新宇董洪祯
张虹,张一帆,王新宇,董洪祯
(北京理工大学 机械与车辆学院,北京 100081)
涡轮在工作过程中,需要承受周期性气动激振力的作用,容易产生振动,导致疲劳破坏,严重制约了涡轮的使用寿命,振动失效问题是涡轮可靠性研究的主要方向之一.扫频试验是研究振动问题的重要手段,试验时激励的频率随时间变化,可以对产品的振动可靠性进行检验,也可根据试验数据获得产品的共振频率和阻尼等信息,该方法已广泛运用于汽车、航空航天等领域[1-3].
涡轮的扫频试验一般采取控制转速逐渐变化的方式,改变所受气动激振力的频率,最终通过测量叶片的振动幅值获得涡轮振动特征参数[4-5].但扫频振动属于非稳态振动,振动特征与稳态特性存在差异,这会导致参数估计误差的存在.国内外学者对于该问题已开展了较多工作,LOLLOCK[6]探究了扫频速率对共振频率和阻尼参数估计的影响,高强等[7]推导了一个扫频参数用于扫频速率的设置和响应数据的修正.但这些研究大多都是基于理论分析,较少针对于涡轮这种复杂对象.因此,寻找一种方法对涡轮的扫频振动特征进行研究具有现实意义.
数值方法是研究涡轮振动特征的重要手段,且已比较成熟.施新等[8]采用数值方法,研究了叶片表面压力波动的形成机理,结果表明压力波动的形成是以冲击波为主导,由叶顶泄露、尾流共同作用所导致的.马朝臣等[9]采用三维非定常周期性计算流体力学模型得到了叶片的各阶谐波激励,发现前两阶谐波是造成涡轮振动的主要激励分量.SCHWITZKE等[10]使用数值方法研究了影响气动响应的关键参数,结果发现,气动响应的幅值与气动激励的幅值、分布函数以及叶片的阻尼有关,气动响应与气动激励的幅值呈正相关,与阻尼呈负相关,分布函数与叶片的振型匹配也会产生较大影响.但是,这些数值分析的对象都是稳态振动,对于扫频激励下的非稳态振动研究较少,原因在于,涡轮的振动频率高、扫频周期长,导致使用数值方法对涡轮在扫频工况下的振动特性进行计算需要巨量的计算步,当前计算资源不足以满足要求.但将其等效为易于计算的单自由度系统是一个可行的方法,该思路已广泛运用于建筑构件的动态响应分析[11-13].
文中以某航空用冷却涡轮为对象,利用非线性谐波法构建的时域结果,根据能量原理,提出了针对该涡轮的等效单自由度计算方法与模型,以研究涡轮在扫频激励下的振动响应特性.
1 等效单自由度方法
根据模态叠加法的原理,涡轮在激振力下的振动响应位移主要由i阶振型组成,而每个振型的形状又是确定的,因而如果能够确定涡轮上某一点振动响应中各阶模态的分量,就可以通过振型转换获得整个涡轮的振动响应,这就是等效单自由度方法.对于涡轮而言,其振动响应位移Q(t)可由广义坐标q(t,n) 和第i阶归一化振型 Φ(n)表示为
式中:t为时间;n为振型阶次.
等效单自由度方法可以通过系统中的一个点建立等效单自由度振动系统,单自由度系统中该点的位移、速度、加速度等参数与实际结构该点的参数在每一瞬间保持一致,通过单自由度系统可以快速求解出实际结构的振动响应参数,计算效率大为提升.简谐激振力作用下的等效单自由度系统由4 个参数组成:等效质量ms、等效阻尼系数cs、等效刚度ks以及等效载荷Fs,如式(2)和图1 所示.
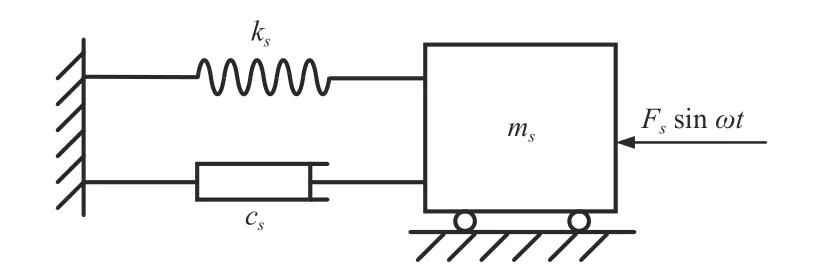
图1 单自由度系统Fig.1 Single-DOF system
等效参数是运用能量原理获得的,单自由度系统4 个参数分别由实际结构的动能Ek、势能Ep、耗散能量Ec以及输入能量EF计算得到.
涡轮结构复杂,等效单自由度系统建立所需参数可通过数值方法获得.首先获得涡轮表面的激励分布和模态信息,确定主要的激励阶次和模态振型;而后进行稳态动力学计算,得到各阶模态的相关参数;对各阶模态分别建立等效单自由度系统并按照模态叠加原理进行叠加;建立Simulink 仿真模型,分析涡轮扫频响应特性.总流程如图2 所示.

图2 等效单自由度系统建模流程Fig.2 Flow chart of SDOF modeling
2 稳态动力学分析
2.1 涡轮表面激励计算
图3 所示为所研究冷却涡轮的三维几何模型,涡轮共有6 组长短叶片,带有17 支沿周向均匀分布的喷嘴环.涡轮喷嘴进口处半径47.5 mm、喷嘴出口半径39.0 mm;涡轮进口半径36.5 mm、出口处轮缘半径27.5 mm、轮毂半径10.3 mm.

图3 涡轮几何模型Fig.3 Turbine geometry model
涡轮内非定常流场分析采用NUMECA FINE/TU RBO 软件,利用非线性谐波法求解涡轮表面的各阶谐波激励;流固耦合基于MPCCI 耦合平台,对流体域网格节点上的气流压力波动作快速傅里叶变换,将变换后的频域气压信号耦合至对应的固体域网格节点;结构分析采用Abaqus 软件,通过MPCCI 耦合平台从流场气动计算结果中提取载荷边界,进行涡轮的谐响应分析,获取涡轮在各阶谐波激励下的动应力.由于无法事先确定诱发涡轮共振对应的涡轮工作转速,因此在计算过程中采用扫频的方法,在特定频率段内对涡轮叶片应力进行计算,确定不同频率下涡轮叶片应力值.
流体域计算网格采用周期性边界,计算域内包含一个喷嘴及一组涡轮通道,绘制结构化网格与边界层网格;固体域网格包括涡轮与喷嘴环网格,如图4 所示.涡轮工作转速为57~ 99 kr/min,计算工况选取最高转速99 kr/min、进口温度58℃、进口压力1 114 kPa、出口压力198 kPa、膨胀比7.05.据此可得到涡轮非定常流场计算结果,如图5 所示.
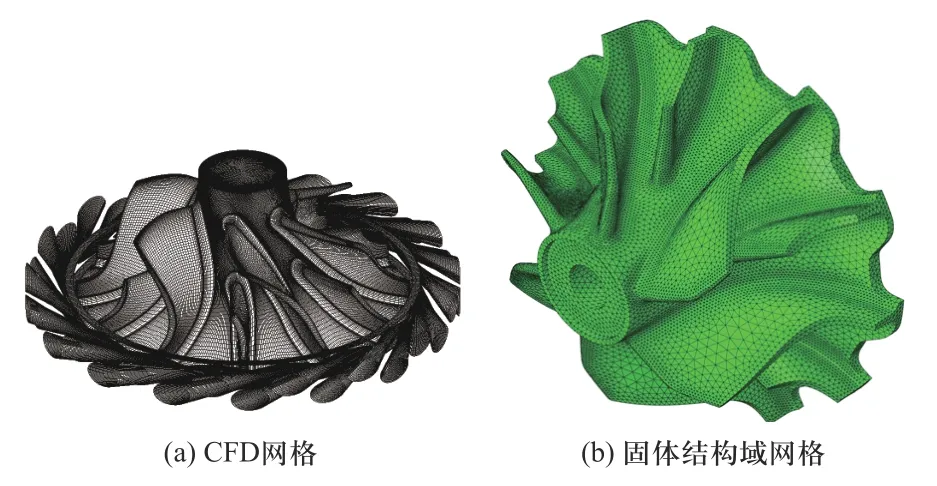
图4 有限元计算网格Fig.4 FEM calculation mesh

图5 涡轮非定常流场计算结果Fig.5 Turbine unsteady flow field
图6 和图7 分别给出了99 kr/min 转速下前两阶谐波对应的压力脉动幅值,1 阶谐波为喷嘴通过频率基频(17 支喷嘴,28.05 kHz),幅值为83 kPa,出现在涡轮进口处;2 阶谐波为2 倍喷嘴通过频率(56.1 kHz),幅值为64.8 kPa,出现在涡轮进口处.可以看出,由于喷嘴的存在,涡轮表面尤其是在涡轮进口位置出现了非常强的高频压力脉动,可能会对涡轮的振动可靠性造成影响.相较而言,一阶谐波的幅值更高且分布区域更为广泛,可认为是主要激励源,在后续研究过程中作为考虑对象.

图6 涡轮表面一阶气动激励云图(99 kr/min)Fig.6 The first order aerodynamic excitation on the turbine surface(99 kr/min)

图7 涡轮表面二阶气动激励云图(99 kr/min)Fig.7 The second order aerodynamic excitation on the turbine surface(99 kr/min)
在扫频过程中,涡轮升速或降速过程将导致其表面气动激励的变化,因此有必要分析转速变速过程对涡轮表面气动激励的影响.计算90 kr/min 稳态工况涡轮表面激励幅值如图8 所示.
对比99 kr/min 结果,90 kr/min 表面激励幅值略小,总体分布基本一致.因此建立等效单自由度模型时,可认为转速在小范围变化过程中,涡轮表面的气动激励变化较小,进而简化气流激励,使用99 kr/min稳态工况激励幅值的变频气动激励作为升速或降速过程的激励.
2.2 模态分析
涡轮材料使用在航空和航天工业中广泛运用的TC4 钛合金,密度为4 440 kg/m3,弹性模量为109 GPa,泊松比为0.33.网格类型选用C3D10M 网格,约束轴孔全部自由度.特征值求解器采用Lanczos,范围为0~60 kHz.根据模态计算结果绘制涡轮振动的Campbell图,如图9 所示.其中阴影区域为工作转速范围,r为气动激励阶次,f为涡轮模态频率,方框区域为后文扫频工况频率与转速范围,斜向激励线与频率相交表示气动激励频率与模态频率相等,初步满足涡轮共振条件.

图9 涡轮Campbell 图Fig.9 Turbine Campbell diagram
可以看出,旋转对称结构的涡轮存在着重频模态,导致满足激励力频率与模态频率的交点数量较多.但涡轮要想被完全激发共振,需要激振力频率等于模态频率且振型节径数满足式(7)要求[14].
式中:r为谐波阶次;NV=17 为喷嘴数;NB=6为叶片组数;d为振型节径数,其中节径数不超过叶片组数的一半,在该涡轮中,由于涡轮最大节径数为3,满足式(7)的涡轮共振条件为r=1且d=1,即一阶谐波激励会发生一节径振动模态,在最高转速内可能的共振频率为24 972 Hz,模态振型为长叶片二阶弯曲加进口处轮毂弯曲,幅值出现在涡轮尾缘叶顶位置,因此该位置应存在较大的由振动弯曲导致的应力.
如图10 所示为涡轮谐响应等效应力幅云图,其中等效应力幅为涡轮在谐波激励下共振时产生的振动应力的变化幅度.等效应力主要分布于叶片尾缘叶顶,幅值为44.099 MPa,该位置的振动应力交变频率较高,易导致叶片失效.将各个方向的位移矢量叠加得到等效位移值,以便更好地评估结构在特定振动模态下的总体振动程度,如图11 所示.从能量输入的角度来看,输入能量与激励压力脉动和结构位移幅值的乘积呈正比.对于该阶模态,发生变形的进口轮缘处和长叶片约50%弦长处与一阶气动激励的高压力脉动区重合,在一阶气动激励作用下产生较大振动响应可能性较高.
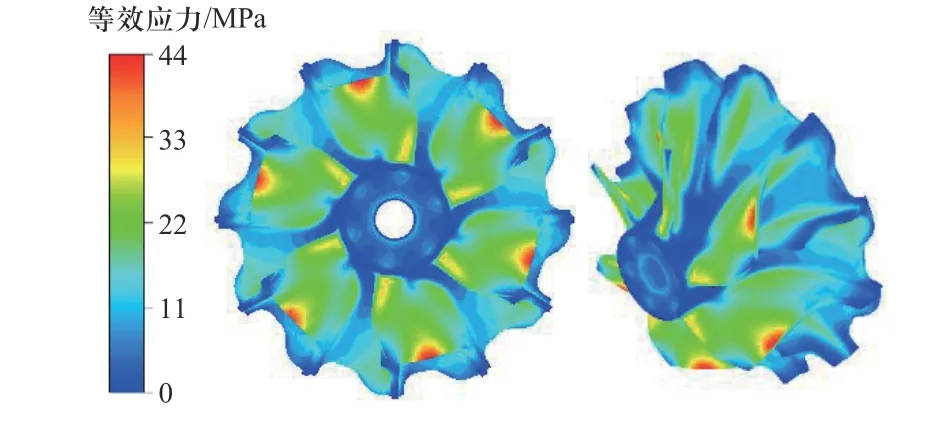
图10 谐响应等效应力幅云图Fig.10 Harmonic response equivalent stress amplitude contour
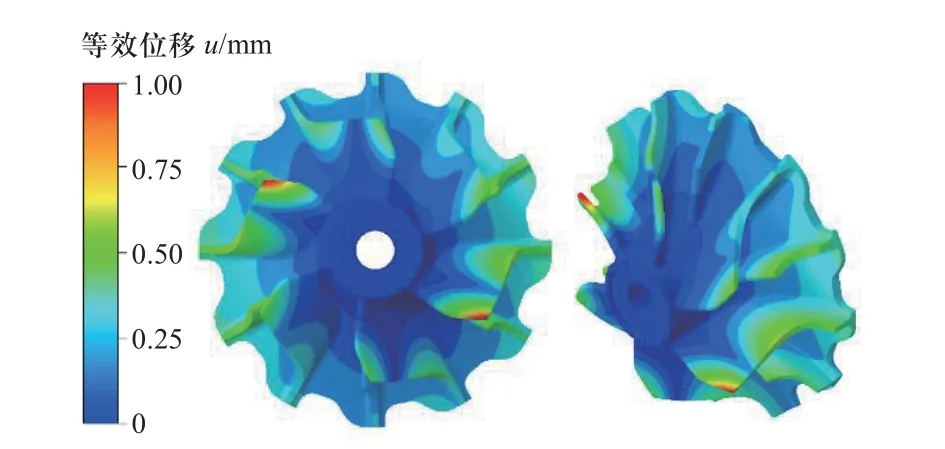
图11 涡轮共振模态等效位移云图Fig.11 Equivalent displacement of modal shapes
2.3 谐响应分析
谐响应计算网格和约束与2.2 节相同,计算方法采用模态叠加法.阻尼采用Rayleigh 阻尼,即
式中:C为阻尼矩阵;M为质量矩阵;K为刚度矩阵;在本式中取 α=0 ; β=2.27×10-7.
将2.1 节计算得到的一阶压力脉动幅值和分布加载至流固耦合面,其中流固耦合面包括涡轮与工质接触全部表面.流体域和固体域之间网格不匹配,数据交换采用形函数插值方法.涡轮的谐响应计算采用模态叠加法,计算范围设置为20~30 kHz.
图12 为一阶谐波激励下涡轮尾缘叶顶位置(图13中a 点)的频率响应曲线,其中f1、f2表示两响应峰对应的频率,分别为f1=24 972.7 Hz、f2=28 435.5 Hz.
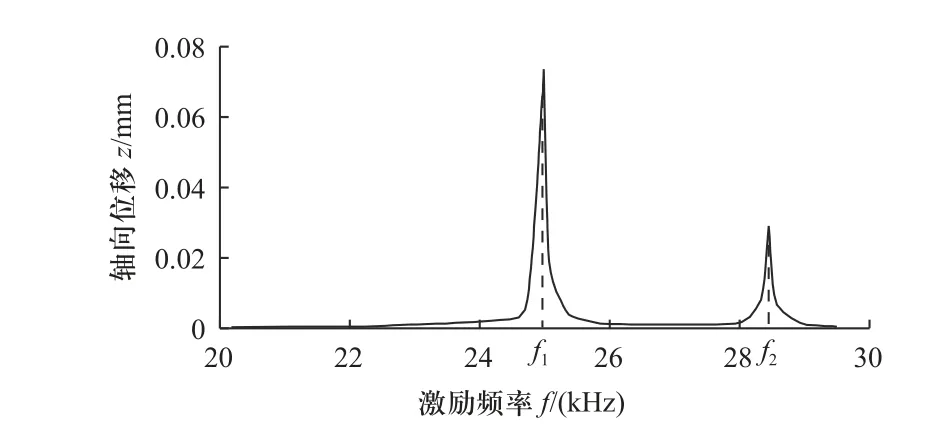
图12 涡轮频率响应曲线Fig.12 Impeller frequency response curve

图13 涡轮轴向位移响应云图Fig.13 Axial displacement response contour
由于最高转速99 kr/min 对应激励频率为28 050 Hz,据图12 可以看出,在最高转速之内,涡轮在24 972.7 Hz激励下出现了一个响应峰值,即为共振频率.共振频率下涡轮的响应振型与2.2 节获得的模态振型基本一致,是模态分析振型的同比缩放,最大轴向位移达到了0.075 mm,出现在叶顶尾缘位置,如图13 所示.
3 等效单自由度系统建模
3.1 等效单自由度参数
涡轮尾缘叶顶位置前5 阶模态在一阶气动激励作用下的稳态振动响应如表1 所示.实际上,当系统达到稳态之后,动能和势能的幅值相等,每循环的耗散能量与输入能量相等.

表1 涡轮稳态振动响应Tab.1 Steady state vibration response of impeller
根据式(3)~(6),计算得到涡轮前5 阶模态的等效单自由度参数,如表2 所示.

表2 等效单自由度参数Tab.2 Single degree of freedom equivalent parameter
各阶模态叠加时还要考虑响应相位的影响.如2.2 节所述,输入能量需要同时考虑压力脉动分布和模态振型,而每阶模态的主要能量输入位置不同,同时涡轮表面各处压力脉动存在相位差,进而造成各阶模态振动响应的相位差.例如,一阶模态的主要能量输入位置位于涡轮约50%弦长处,而二阶模态的主要输入位置位于轮毂进口处,两处压力脉动幅值存在相位差异,导致了两模态的响应相位差.存在相位差的另一原因是等效单自由度考虑位置(图13 中a 点)与主要能量输入位置之间的相位差,如二阶模态的轮缘进口位置与尾缘叶顶位置存在反相.
根据有限元谐响应分析的计算结果,得到等效单自由度模型1~5 阶模态的相位差分别为0°、180°、240°、180°、180°.
单自由度响应计算采用Simulink 可视化仿真工具,仿真算法采用ode45,可变时间步长.由于Simulink 建模时多采用积分形式,因此将式(2)变换为式(9),易于理解.
根据式(9),考虑到轴向振动较其他方向而言会对涡轮的性能产生较大影响,建立涡轮轴向单一模态等效单自由度模型,各参数根据以上数据输入,如图14 所示.如此可得到每个子系统的响应位移q(t,n).依次建立各模态等效模型,依据式(1)将每个子系统的响应位移q(t,n) 与相应的振型 Φ(n)相乘,然后对所有子系统求和,可得到整体涡轮的响应位移Q(t).

图14 单一模态等效单自由度模型Fig.14 Model of single-mode equivalent single degree of freedom
3.2 等效单自由度方法验证
采用等效单自由度模型计算涡轮在气动激励下的定常强迫振动响应,对比有限元模型的谐响应计算结果,验证等效单自由度模型的可行性.考虑提高对比结果的准确性,在20~30 kHz 激励频率范围内,每隔约2 kHz 取一个计算点,外加共振位置24 972.7 Hz和28 435.4 Hz,总计8 个计算点.
从表3 中可以看出,除30 kHz 以外,等效单自由度模型和有限元模型之间的误差较小,都在10%以内,有着较高的准确性.可以认为,等效单自由度模型能够较好匹配有限元模型,可用于振动研究.
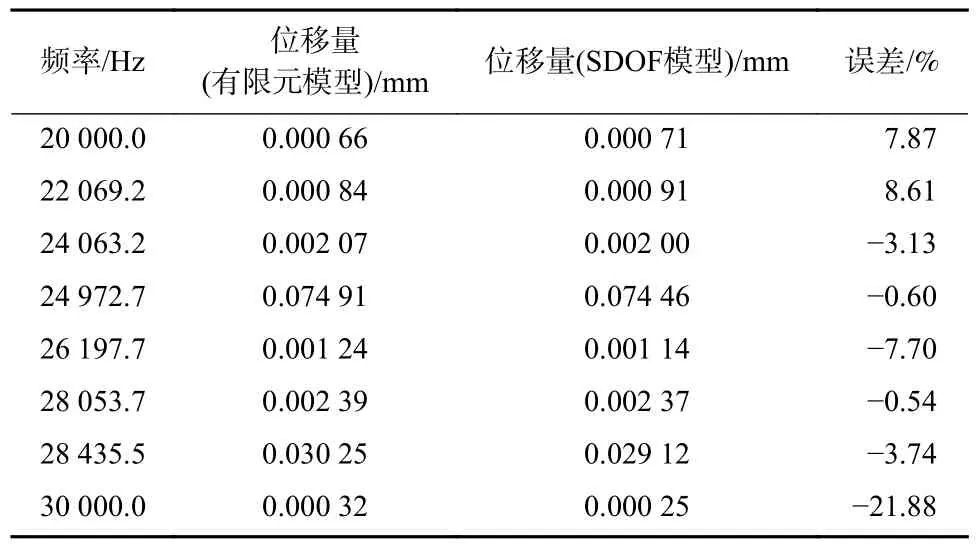
表3 单自由度模型和有限元模型结果对比Tab.3 Comparison between single degree of freedom model and finite element model
等效单自由度模型与有限元模型产生误差的原因主要在于:①等效单自由度模型在建立时,最高只考虑到了30 958.1 Hz 模态,更高阶则没有考虑,而有限元模型在计算时频率最高提取到60 kHz,因此产生了截断误差,这也是激励为30 kHz 时误差较大的原因;②等效单自由度模型在建立时只考虑了可能会发生共振的一节径振动模态,忽略了其他振动模态.在共振频率附近,发生共振的一节径模态的响应值远远大于不会发生共振的其他模态,因此不会对结果产生较大影响,其他位置则有可能变大.
4 扫频振动特征分析
通过建立的涡轮等效单自由度模型,分析研究线性扫频工况下与稳态工况下涡轮的振动响应差异,根据式(7)结果,选定涡轮第一阶模态作为分析对象,扫频范围选择23~27 kHz(81 176 ~95 294 r/min),扫频方式为频率线性增加.该范围内其余模态影响较小,分析时只考虑一阶模态作用即可.单自由度系统在简谐激励作用下的稳态振动响应如式(10)所示.[15]
式中:X为稳态位移幅值;F为激励幅值;m为质量;k为刚度;c为阻尼系数; ω为激励频率.为提高后续分析精度, ω步长选为0.01 Hz,得到稳态位移幅值随激励频率 ω变化对的曲线如图15 中黑色曲线所示,响应峰值出现在24 972.7 Hz 处,响应幅值0.074 90 mm,半功率带宽为24 950.4~24 995.1 Hz.为避免由两种算法带来的误差,使用Simulink 同样计算24 972.7 Hz的稳态响应幅值,结果为0.074 89 mm,误差很小可以忽略.
以1 s 为扫频时长,线性扫频激励下响应幅值与稳态激励下对比如图15 所示,图15 中蓝色曲线为扫频响应,响应峰值位置为25 008.0 Hz,右移(增大)35.3 Hz,响应峰值大小为0.065 66 mm,相较稳态响应减小0.009 24 mm,占比约12.3%,半功率带宽为24 976.2~25 017.7 Hz.可见,对于该涡轮而言,从23 kHz 线性增加到27 kHz,1 s 是一个较长的时间,激励频率扫频得到的响应参数与稳态参数能够较好地吻合.从图15 中可以看出,在扫频响应峰值之后出现了拍振现象,这是由于该频率下同时存在初始条件为响应峰值的有阻尼自由振动和受迫振动,二者叠加导致其响应形状与稳态响应存在差异.
如图16 所示为涡轮响应峰值和半功率带偏移图.可以看出,响应峰值位置随扫频时间的减小而逐渐增大,但受影响程度不大,即使扫频时间为0.062 5 s时,偏差也不超过1%.半功率点随扫频时间的减少也相应偏移,且带宽增加明显.
结合图15,由于拍振现象,响应峰值后振幅衰减明显,导致响应峰值左侧半功率带宽度明显大于右侧,且扫频时间越短越明显.可以认为,使用半功率带宽法测量阻尼时误差受扫频速度影响较大,而共振频率估计则相对不敏感.
使用上述参数对系统进行逆向扫频,结果如图17和图18 所示.可以看出,不同扫频时间下,正向逆向扫频的半功率带和响应峰值的偏移程度基本一致但方向相反.因此,使用扫频方法获得系统的共振频率时,可采用正向、逆向扫频后求平均的方式提高精度.
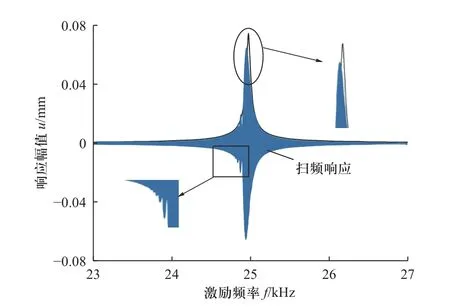
图17 扫频响应与稳态响应对比(逆向)Fig.17 Sweep-frequency response VS steady-state response (Backward)

图18 响应峰值和半功率带偏移(逆向)Fig.18 Formant and half power bandwidth offset (Backward)
如图19 所示,图中圆点为正向扫频响应峰值,方点为逆向扫频相应峰值,实线为稳态响应峰值,虚线为扫频响应拟合曲线.对比两向扫频结果可知,在相同扫频时长下,正向、逆向扫频的响应峰值相同,即响应峰值大小与扫频方向无关.

图19 不同扫频时长下响应峰值对比Fig.19 Comparison of response amplitude at different sweep-frequency time
拟合扫频响应曲线,可得到如下结果:
其中R2为相关系数,接近1 时表示拟合函数与数据点吻合度高.由拟合函数可知,响应峰值大小与扫频时间在计算范围内大致呈对数关系,扫频时间越长,响应峰值越大.此外对比扫频工况与稳态工况的响应峰值可知,随扫频时间增加,扫频工况下响应峰值增大,且其值逐渐靠近稳态响应峰值.
5 结 论
文中使用流固耦合方法计算了涡轮的稳态振动参数,根据计算结果建立了等效单自由度模型,将该模型计算结果与有限元稳态计算结果进行了对比验证,并分析了扫频工况下的瞬态振动,结果表明:
①等效单自由度模型能够较好地复现流固耦合方法的计算结果,与有限元计算得到的响应结果误差小于10%.该方法对于涡轮的振动研究是一种可行的方法;
②与稳态响应相比,正向线性扫频激励下涡轮响应峰值频率增大,半功率带宽变宽,响应峰值后将出现“拍振”现象;
③各项参数中,半功率带宽对扫频速度最为敏感;正向、逆向线性扫频激励下涡轮响应偏移程度相较稳态响应基本一致;在一定范围内,响应峰值大小与扫频时间大致呈对数关系,扫频时间越长,响应峰值越大.
通过文中研究,建立了冷却涡轮单自由度等效模型,经过对比可证明通过扫频方法分析涡轮振动响应是可行且有效的.
