多箱型结构内部爆炸破坏模式分析方法

李璐萌，张舵，姚术健，黄诗麒，黄河

（1.国防科技大学 理学院，湖南，长沙 410073；2.军事科学院 国防工程研究院，北京 100036；3.中南大学 交通运输工程学院，湖南，长沙 410083）

随着侵爆类武器精度的提高，结构内部爆炸成为武器毁伤的主要模式之一.密闭和半密闭的结构内部爆炸引起的破坏效应明显区别于结构外部爆炸，由于结构和爆炸的相互作用，结构破坏、冲击波反射、爆轰产物扩散等效应相互耦合[1]，过程非常复杂.为了研究舰船舱室、建筑物房间和钢箱梁大桥等结构的内部爆炸破坏机理，本文针对简化的多箱型结构内部爆炸问题，系统地研究其破坏机理和破坏特性，为建筑物和舰船等多箱型结构的破坏特征和抗爆加固、侵爆类弹药毁伤效果预测和毁伤效能评估提供基本方法支撑.

爆炸发生后，由于结构内壁面的反射作用，内部爆炸载荷一般包括多个压力脉冲，冲击波的汇聚和叠加效应，造成内部爆炸压力载荷波形较为复杂.冲击波反射多次后逐步稳定，爆轰产物在结构内部均匀分布形成准静态压力[2-3].研究表明，准静态压力峰值取决于装药空间密度，是W/V(W为等效TNT 药量，V为空间体积)的函数[4]，并会随着气体外泄而逐渐降低，作用时间由泄压面积决定[5].冲击波和准静态压力的共同作用会使内部爆炸的破坏效果更强[6]，构件的破坏机理和效应更加多样化.

结构内部爆炸作用下结构的破坏模式也有所不同，MENKES 等[7]根据冲击载荷的不同，将梁的破坏模式分为塑性大变形、支承处拉伸破坏和支承处剪切破坏等3 种模式.随后JONES[8]对MENKES 等的实验进行了深入研究，预测了模式之间的临界条件和速度阈值，并通过理论推导的方法验证了MENKES 和OPAT 的实验结论.YONG 等[9]通过实验和数值仿真发现上述破坏现象和模式在箱型结构内爆中也会出现.YAO 等[10-11]总结内部爆炸作用下箱型结构的破坏模式，并采用量纲分析得到预测经验公式，进一步研究了多箱型结构的破坏.爆炸当舱壁板破坏变形会引起箱室内高压气体扩散到临近箱室，造成进一步破坏，同样，结构对爆炸能量也有约束和导向作用.汪维等[12]通过钢结构内爆试验，对钢结构箱体在内部爆炸荷载作用下的破坏模式和破坏等级进行了分析.李樱等[13]运用数值仿真研究了不同舱段结构在水下爆炸作用下的毁伤特性，定量分析了破口大小与结构毁伤模式.余俊等[14]对舰船结构缩比模型进行了内部爆炸实验研究，发现在小当量内爆作用下多箱型结构呈现十字形的破坏特征.各向异性（不同方向材料或（和）结构尺寸不同）多箱型结构在多样的内爆载荷作用下会引起不同破坏效应，造成不同的整体破坏模式，但是相关机理性基础研究还较少.

通过前期分析，发现爆炸破坏模式和破坏范围并非随着爆炸当量的增加而连续变化，而是呈现出在某些当量下模式和范围发生突变的现象，本文采用有限元模拟仿真分析，研究了结构几何尺寸、强度与爆炸载荷对整体破坏模式的影响，基于模拟仿真结果，推导出具有明确物理意义，能够预测多箱型结构破坏箱室数、破坏壁面数和毁伤模式的无量纲数，绘制出破坏分布模式图和破坏范围表，并根据已有实验结果验证了所提出的预测方法.在研究爆炸载荷作用下的结构响应时，NGO 等[15]指出持续时间更长的横向荷载（准静态）主要影响结构构件的整体响应.杜志鹏[6]认为冲击波峰值高但持续时间短，主要产生初期的局部花瓣破口和板架边界撕裂；准静态压力幅值较低，但持续时间较长，对整个箱型结构强度产生主要影响.目前研究普遍认为冲击波主要引起爆炸当舱破坏，爆轰产物气体和准静态气体压力是造成更大破坏范围的主要原因[16-18].

1 多箱型结构内爆毁伤特性有限元仿真

1.1 仿真模型构建

参考文献[19]中的单箱型结构模型构建方法和材料参数设置， 建立更大范围的多箱型结构.整个多箱型结构由于三维模型计算上的限制，实用性有限，无法用作工程工具.为了更加清晰揭示结构内部爆炸引起的破坏模式，本文简化周期多箱型结构，参照文献[20 - 21]建立准二维有限元计算模型（一个狭窄的计算区域），约束狭窄区域两侧的法向（如图1 中Y轴方向）自由度，从而系统地分析内部爆炸载荷对多箱型结构的破坏效应.运用 LS-DYNA 有限元软件仿真计算，使用ALE 多物质流固耦合算法，通过设置高压气体参数模拟内爆载荷，来研究不同壁厚的多箱型结构在不同当量的中心内爆作用下的整体破坏模式.

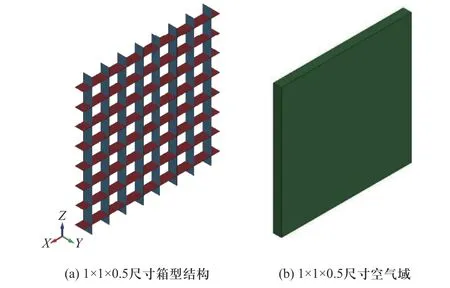
图1 有限元模型Fig.1 Finite element model

1.1.1 有限元模型

考虑8×1×8 个多箱型结构，每个箱室长1 m、高1 m、宽0.5 m，设置为5 mm 和8 mm 两种板厚.参照舰船箱室钢箱结构，箱体模型使用SHELL163 单元，空气和高压气体使用SOLID164 单元，使用流固耦合算法.结构及空气域网格尺寸为4 cm，多箱型结构总共划分563 264 个单元，其中箱体有 43 264 个，空气与高压气体有520 000 个；箱体固定节点Y轴方向移动和X、Z轴方向旋转，空气域在Y轴方向前后边界设置固壁边界条件，如图1 所示.

1.1.2 材料模型与参数

空气域和高压气体填充域均采用空物质材料模型（MAT_NULL）和气体线性多项式状态方程（EOS_LINEAR_POLYNOMIAL）描述[22]：

式中：p为压力；Ei为单位体积内能，单位为J/m3；µ=ρ/ρ0-1 ， ρ0为初始密度， ρ 为t=0 时的密度；C1=C2=C3=C6=0，C4=C5=(γ-1)=0.4 ， γ 为 比 热 容 比.空气域内能Ei为0.25 MPa，设置高压气体压力为6.25～100 MPa，通过设置高压气体参数模拟不同当量中心内爆.对比算例中使用炸药填充，炸药采用高能燃烧模型（C-J 模型）和JWL 状态方程描述，利用关键字*MAT_HIGH_EXPLOSIVE_BURN*定义[22]，材料参数如表1 所示.

表1 TNT 材料模型及状态方程参数[23]Tab.1 Mechanical properties of TNT

箱体材料选用Q235 低碳钢，模型采用双线性弹塑性*MAT_PLASTIC_KINEMATIC*本构模型, 材料的应变率效应由 Cowper-Symonds(C-S) 模型描述为

式 中： σd为 动 态 屈 服 强 度； σ0为 静 态 屈 服 强 度；E为弹性模量；Et为应变硬化模量；为有效塑性应变； ε˙ 为 等效塑性应变率；C、P为应变率相关的常数.材料失效模型采用最大等效塑性应变失效=ln(1+δs) ，其中 δs为延伸率.参数设置如表2 所示，其中ρ为材料密度，ν为泊松比，Fs为失效应变，此时删除单元.

表2 Q235 钢材料模型参数[24]Tab.2 Mechanical properties of Q235B steel plate

1.2 内部爆炸载荷模拟方法

炸药爆炸常采用高能燃烧模型JWL 状态方程描述，利用关键字*MAT_HIGH_EXPLOSIVE_BURN*定义：

式中：p为爆轰压力；为相对体积，v为 比容，v0为初始比容；Ei为单位体积内能.其中方程式右端第一项在高压段起主要作用，第二项在中压段起主要作用，第三项代表低压段.在爆轰产物膨胀后期，方程式前两项的作用可以忽略，为简化计算，采用理想气体状态方程代替JWL 状态方程对爆轰产物进行快速求解[25].基于内能等效原理，设置高压气体填充区域内能，填充至箱体中心模拟不同当量中心内爆

式中：Eh为高压气体内能；Etnt为炸药内能.联立式（1）、（3）和（4）得到高压气体内能Eh和压力p满足

式中：Eh和p分别为高压气体内能和压力；Vx为高压气体填充箱室体积.BAKER 等[26]认为压力荷载可以独立于时间施加，并用简化算法来表示内部爆炸荷载.周杰等[27]将高压气体填充至发生爆炸的箱室，模拟不同的内爆载荷.WEIBULL[4]认为可将较长持续时间的准静态压力载荷视为作用于整体结构的爆炸荷载.PICKERD 等[16]对比研究了初始加载与冲击波反射和准静态加载相比的定性效果，使用相似方法在结构内部填充高压气体模拟结构内部爆炸，对比发现与构件在炸药爆炸作用下的变形程度相近.DRAGOS 等[28]将约束爆炸载荷基于冲量相等的方法简化为准静态载荷，发现对于构件响应时间非常短的爆炸荷载，简化荷载比实际爆炸荷载引起的破坏性挠度小，但对于响应时间较长的构件，简化方法非常准确.该方法重点考虑内爆载荷对整个壁板及箱型结构的破坏效应，简化炸药爆炸和冲击波传播过程中能量衰减的过程，忽略冲击波对壁板不同区域作用强度的差异，突出多箱型结构内部爆炸的主要影响因素，忽略次要因素，节省计算时间与资源.

如图2(a)所示，按照壁板主要承受作用力方向，将多箱室结构中的隔板分为横向受力板和纵向受力板.如图2(b)所示，在炸药当量W=15 kg 和高压气体p=39 MPa 作用下，纵向受力板破坏程度相似，横向受力板的破坏模式不同，破坏壁板数量相同.计算结果中两种填充方法在爆炸当舱和横向受力板的破坏模式不同，在本文研究主要关注的多箱型结构整体破坏模式和破坏范围方面相似.两种填充方法的破坏结果存在区别，是由爆炸当舱破坏与结构整体破坏的主要原因不同导致（冲击波对爆炸当舱的破坏起主要作用，准静态压力对结构整体的破坏起主要作用[6]），高压气体填充时主要考虑了爆轰产物膨胀后期的准静态压力载荷[29].经过大量对比算例验证，认为该方法能够研究多箱型结构在内部爆炸载荷作用下的整体破坏情况及其影响因素.本文以2～40 kg的TNT 在尺寸（长×宽×高）为1 m× 1 m× 0.5 m 的Q235钢制多箱型结构中心发生爆炸为例，研究破坏范围和破坏模式随当量和结构参数的变化规律.参考文献[23]，TNT 炸药密度为1 601 kg/m3，内能为6.0 ×109J/m3，代入式（3）和式（4）得到高压气体压力为5～100 MPa，填充至多箱型结构中心，研究不同当量炸药发生中心内爆后，多箱型结构整体的破坏模式和破坏范围变化规律.

图2 炸药填充与高压气体填充箱型结构毁伤效果Fig.2 Damage effect of explosive-filled and high-pressure gas-filled cabin structure

2 计算结果分析

2.1 不同毁伤模式

在内部爆炸作用下，横向受力板主要承受垂直于板面的作用力（以爆炸载荷压力为主），破坏模式主要有大挠度变形、局部破口、边界拉伸破坏和边界剪切破坏；纵向受力板主要承受平行于板面的作用力（结构传递力），受力后板主要呈现压缩或弯曲，根据纵向受力板在爆炸作用下的破坏情况，将多箱室结构的整体破坏模式分为十字形破坏，类十字破坏以及圆形破坏[30].在当量较小的情况下，纵向受力板呈弹性变形或小挠度变形，不影响其支撑功能，整体结构呈现十字形破坏，如图3(a)所示；随着爆炸能量增加，结构棱角发生花瓣形破坏，整体呈现类十字形破坏，纵向受力板呈严重塑性变形，已基本无法承担支撑作用，如图3(b)所示；当爆炸能量进一步增加，近爆点结构完全屈服，局部呈现近似圆形破坏，纵向受力板被压扁或者炸飞，已完全无法承担支撑作用，并且能量通过泄压口泄出，波及临近房间，如图3(c)所示.

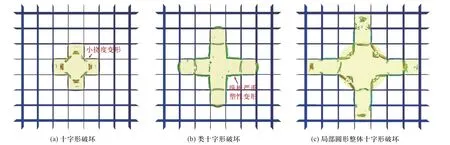
图3 多箱室结构在内部爆炸作用下的破坏模式Fig.3 Damage mode of multi-chamber structure under internal explosion

2.2 爆炸能量对毁伤特性的影响

如图4 所示的是壁厚为5 mm 的Q235 箱型结构在压力分别为20 MPa、50 MPa 和100 MPa 的高压气体作用下的破坏情况.随内爆能量的增加，多箱型结构以爆炸当舱为中心，局部从“十”字形向类“十”字形破坏直至圆形破坏分布转变，整体呈“十”字形破坏分布，破坏范围逐层离散增加.

图4 不同爆炸当量对多箱型结构的破坏程度Fig.4 Damage results of a multi-cabin structure under internal blast loadings

2.3 箱体壁厚对毁伤特性的影响

如图5 所示，压力为100 MPa 的高压气体对不同壁厚多箱型结构的破坏情况.壁厚为5 mm 的Q235箱型结构，局部呈圆形破坏分布，破坏范围为25 个箱室，如图5(a)所示.壁厚为8 mm 的Q235 箱型结构，整体呈类十字形破坏, 破坏范围为17 个箱室，如图5(b)所示.通过增加箱型结构壁厚，相互支撑形成棱角的壁板对爆炸能量具有更好的抵抗和导向作用，能够有效减少多箱型结构的破坏范围和破坏程度.

图5 不同厚度多箱型结构的破坏程度Fig.5 Damage results of the multi-cabin structure with different thicknesses

3 多箱型结构破坏模式图与分析方法

为了得到不同工况下的破坏模式，对不同壁厚的箱型结构在不同内爆能量作用下的工况进行数值模拟计算.多箱型结构在内爆作用下的破坏问题，可以参照破坏箱室数m、破坏壁面数k和多箱型结构整体破坏模式快速分析破坏范围与毁伤效果.

3.1 破坏箱室数分析方法

破坏箱室数m与压力p和结构强度 σ有关，针对各向异性多箱型结构（不同方向壁板材料和（或）结构尺寸不同）提出等效结构强度.为简化分析，从二维多箱型结构入手，如图6 所示，假设纵向板的结构强度σ1、长度a、厚度h1、纵向个数n1；横向板的结构强度σ2、长度b、厚度h2、横向个数n2.

图6 各向异性多箱型结构Fig.6 Anisotropic multi-cabin structure

多箱型结构的等效强度为各类板材料强度与其体积之积的和除以多箱型结构占据的总体积，可以认为是整体结构的等效强度，对于二维多箱型结构，在Y方向尺寸取单位1 的情况下，等效结构强度为

在各向同性箱型结构算例中，横向板与纵向板的材料和尺寸相同，材料强度为σ，板长度为l，厚度为h，横向和纵向数量为n，则整个多箱型结构的等效结构强度 σ 在忽略高阶小量后为

通过理论分析提出能描述结构在内爆作用下的破坏箱室数的无量纲数p/σ˜ (p为压力， σ˜为等效结构强度)，其物理意义是多箱型结构破坏房间数与爆炸载荷和结构整体抗力的相对大小有关，将数值仿真结果绘于图7.

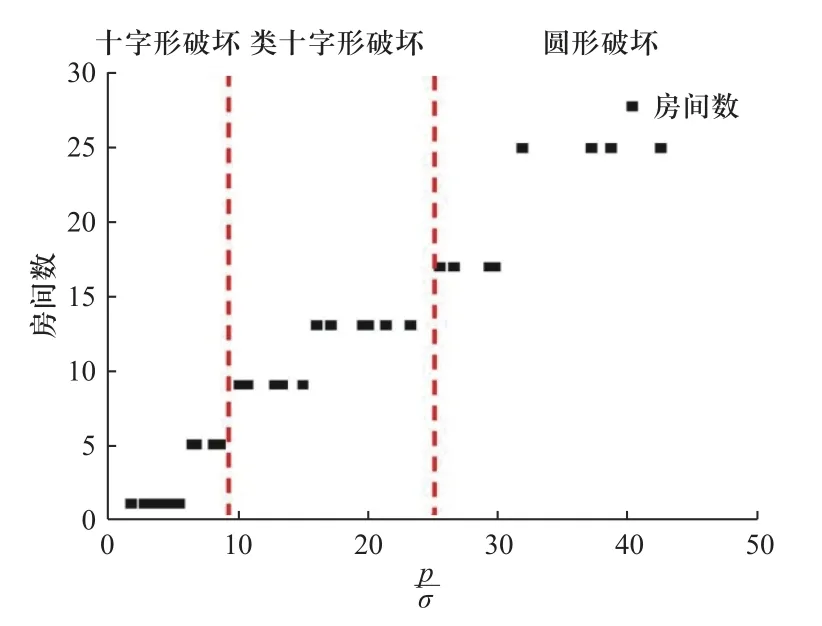
图7 单无量纲数的破坏箱室数分布图Fig.7 Distribution map of the dimensionless number of damaged cabins

对于尺寸（长×宽×高）为1 m×1 m×0.5 m 的二维多箱型结构，在5～100 MPa 高压气体作用下，破坏箱室数m随无量纲数p/σ˜的增大而离散增大.将爆炸工况参数代入，计算出相应的无量纲数，利用以上规律，可快速预测二维多箱型结构破坏箱室数.

3.2 破坏壁面数分析方法

基于对爆炸成形机理的认识，郑哲敏[31]认为爆炸成形系统中能量的传输和分配是问题的关键，并通过细致整理分析大量实验数据，炸药能量与板材总的变形能之比为炸药能量利用率，薄板在爆炸成形时炸药能量利用率相差不多，并提出具有明确物理内涵的能量准则：

式中：Etnt为炸药能量； σ ,δ,l分别为壁板的屈服强度、厚 度 和 长度； ε¯ 为 壁 板平均 应 变；C为 常 数； σε¯δL2为壁板变形能，将能量准则应用于箱型结构内爆问题；ε为破坏应变.

大变形矩形板的应变能Up由弯曲应变能和拉伸应变能组成，利用能量法推导出平板的变形能[32]

式中： ω0为壁板中心挠度； σ 为屈服强度；h,a,b分别为壁板的厚度、长度和宽度.壁板的极限承载力不仅取决于能够承受的最大应力，还与最大应变和极限变形有关，根据材料最大应变进一步推导出中心挠度 ω0的破坏临界值[33]

式中： εmn为材料断裂应变，对于低碳钢， εmn=0.28[24].

根据能量准则，爆炸产生部分能量转化为壁板变形能，且每个壁板的能量利用率相差不多[34].提出能描述破坏壁板数的无量纲数W/UP（W为爆炸成形能量，UP为板材变形能），其物理意义是破坏壁板数为爆炸成形能量与单个板材破坏消耗的变形能的比值，

式中： η为能量利用率，在爆炸成形问题中 η ≈56%[31]；Eh为高压气体内能.

针对1 m×1 m×0.5 m 各向同性多箱型结构算例，每个箱室长度l、宽度0.5l、高度l和体积Vx，壁板厚度h，屈服强度为σ，使用内能为Eh的高压气体填充在多箱型结构中模拟炸药内爆作用，将仿真数据代入式（11）得到破坏壁板数，与能量准则[34]所得结论一致，联立式（5）、（8）和（11）得到壁板破坏壁面数

式中：W为爆炸成形能量； σ,l,0.5l和h分别为壁板的屈服强度、长度、宽度和厚度； ε 为壁板破坏应变.从单个壁板分析，单个壁板所受载荷与有效强度之比能得到相似的无量纲数，在二维各向同性箱型结构中，各壁板结构尺寸和材料相同，压力p与板的有效强度 σ˜ 之比得到的无量纲数p/σ˜ ，其物理意义为板的破坏与作用在上面的爆炸载荷和材料抗力的相对大小有关.

式（13）中压力p与有效强度 σ的比值（无量纲数p/σ˜）和破坏箱室数相关，与式（12）中描述破坏壁板数的无量纲数呈线性关系.基于数值仿真结果计算无量纲数，绘制无量纲数W/Up和p/σ˜与破坏箱室数m、破坏壁板数k和破坏模式的关系图，如图8 和图9所示.

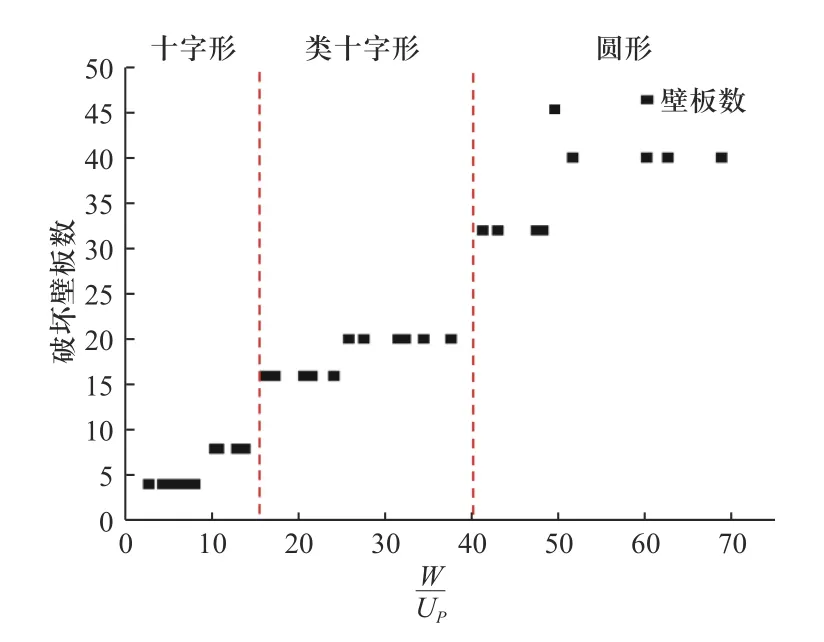
图8 无量纲数的破坏壁面数分布图Fig.8 Distribution map of the dimensionless number of damaged wall plates

图9 无量纲数的破坏壁面数与破坏箱室数分布图Fig.9 Distribution map of the dimensionless number of damaged cabins and wall plates

无量纲数W/Up和p/σ˜能够很好地描述破坏箱室数和破坏壁面数，破坏箱室数m和破坏壁面数k随无量纲数W/Up和p/σ˜的增大而离散增大，且m和k之间存在对应关系，通过式（12）和（13）进行转化.

基于数值模拟，可得出大量不同壁板厚度的多箱室结构在不同内爆载荷作用下的毁伤结果，对应的毁伤范围和破坏壁板数情况如图10 所示.以红色方格为中心，着色方格为受损箱室，红色加粗墙体为破坏壁面，当壁面呈大挠度变形或炸飞时计入破坏壁面数，当箱室两个或以上壁面被破坏时计入破坏箱室数，根据箱室纵向受力板破坏程度（弹性变形或小挠度变形、大挠度变形和压扁或炸飞）区分十字形、类十字和圆形破坏.

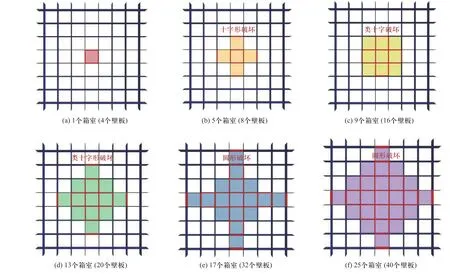
图10 不同破坏箱室数的壁面受损情况Fig.10 The number of damaged walls of multi-cabin structure

如图11 所示为多箱室结构内部爆炸破坏模式图，以红色方格为中心，颜色方格为对应累积附加的破坏范围，颜色实线为壁面破坏情况，随着内部爆炸能量的增加，以爆炸当舱为中心，破坏模式逐层从十字形向类十字形再向圆形破坏转化，破坏范围逐层向外扩展.在不同当量内部爆炸作用下，多箱室结构的破坏范围、破坏模式和计算得到的无量纲数W/UP和p/σ如表3 所示.

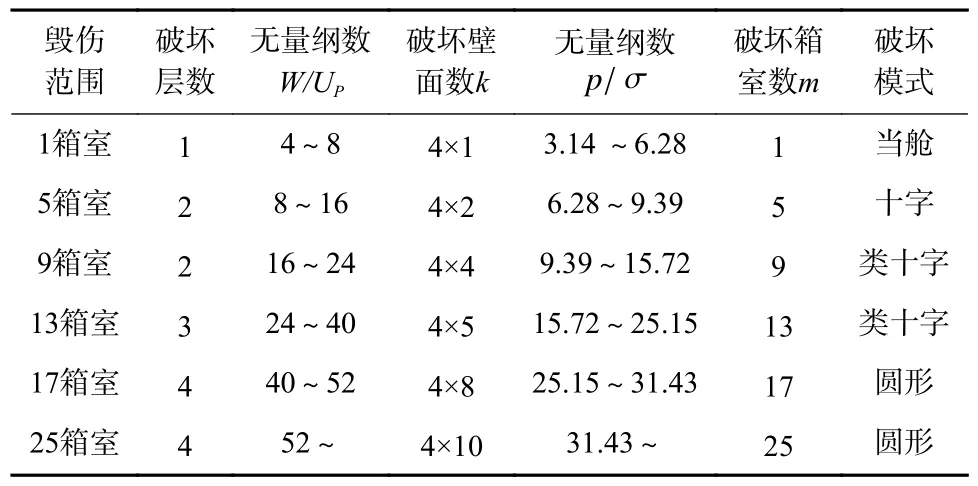
表3 二维各向同性箱型结构破坏范围表Tab.3 Two-dimensional isotropic box structure damage range table

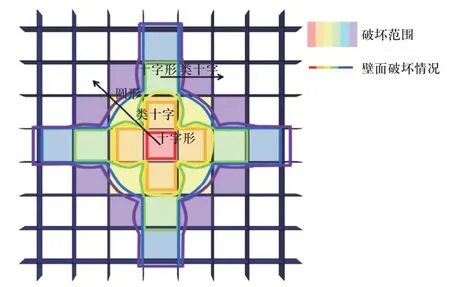
图11 多箱型结构在内部爆炸作用下破坏模式图（箭头表示破坏扩张方向）Fig.11 Damage mode diagram of multi-box structure subjected to internal explosion (The arrow indicates the direction of expansion of destruction)

无量纲数W/UP是爆炸载荷能量与壁板变形能的比值，是随着爆炸当量的增加而连续变化的，但破坏壁面数是量子化离散的，即无量纲数W/UP需超过破坏壁面数每阶段阈值，才能使本阶段破坏壁面数k发生突变.如表3 所示为二维各向同性箱型结构破坏范围表，每个箱体有4 个面，推广到三维各向同性箱型结构，整个多箱型结构X、Y和Z三个方向，每个箱体6 个面，以爆炸当舱为中心，随着爆炸能量的增加，逐层从十字形破坏向类十字形直至圆形破坏转变，结合式（11）和（13），可得到三维箱型结构破坏范围表，如表4 所示.同理，无量纲数p/σ˜是随爆炸当量的增加而连续变化的，但是只有爆炸能量超过每层箱室的抗力阈值，才能破坏下一层箱室，破坏箱室数发生突变，增加箱室数与破坏层数相关.

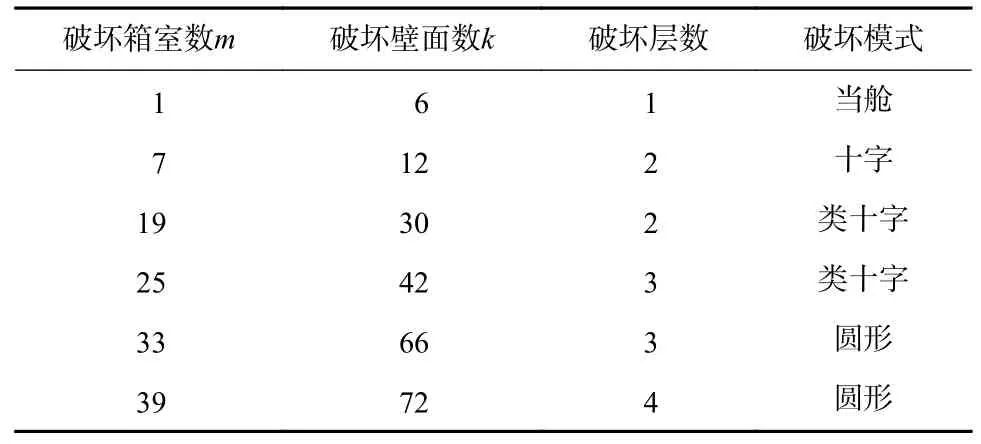
表4 三维各向同性箱型结构破坏范围表Tab.4 Three-dimensional isotropic box structure damage range table

3.3 破坏模式分析方法

多箱型结构整体破坏模式与纵向受力板的破坏情况有关，根据板壳理论[35]，矩形板在两端面受压后将面临弯曲或缩短，由于薄板的法向刚度最低，容易发生法向的挠曲失稳，如图12 所示.

图12 受单向轴力的矩形板[35]Fig.12 Rectangular plate subject to unidirectional axial force[35]

对于单向受压矩形板其屈曲临界应力为

式中：D为弯曲强度，；E为材料弹性模量；h为板的厚度； µ为泊松比；b为板的宽度，当a≫b或a≈b时 , 取k=4 , 当a≪b时, 取k=1.

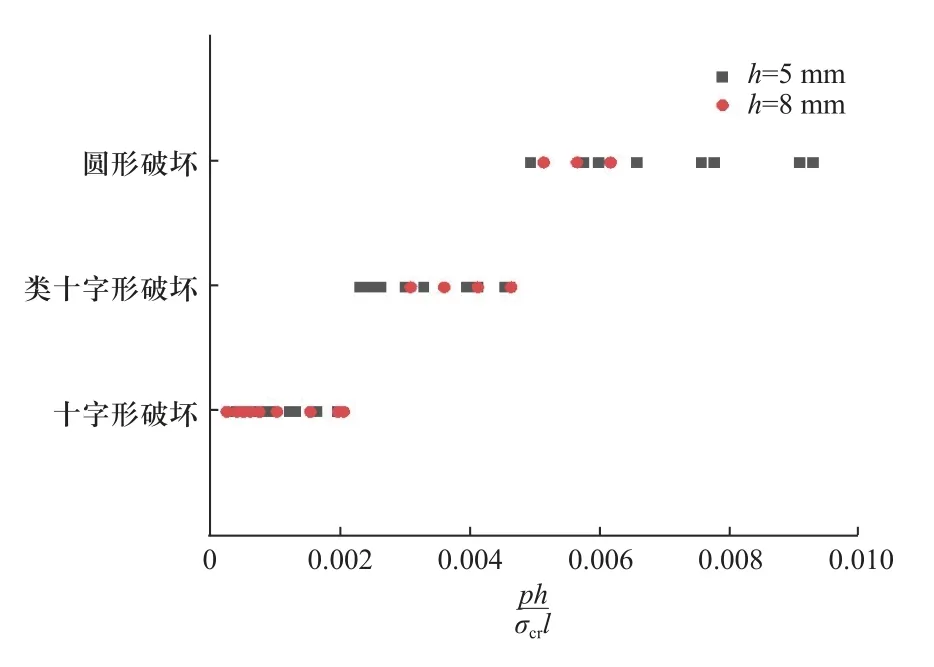
图13 无量纲数的破坏模式分布图Fig.13 Distribution map of dimensionless failure modes

多箱型结构在压力载荷作用下，破坏模式随无量纲数ph/σcrl的增大而离散改变.纵向受力板受到平行于中面的作用力时，主要出现压缩或弯曲变形，测量爆炸临舱层纵向受力板的长度，得到纵向受力板变形量δ，将不同厚度纵向受力板的变形量无量纲化得到δ/l（δ为纵向受力板变形量，l为壁板长度）与无量纲数的关系绘于图14.当载荷较小(ph/σcrl≤0.002 1)时，多箱型结构呈十字形破坏分布，纵向受力板变形量随无量纲数ph/σcrl的增加而增加，且与壁板厚度无明显关系，此阶段纵向受力板在压力载荷作用下主要表现为压缩变形；当载荷较大(0.002 1 ＜ph/σcrl≤0.004 7)时，多箱型结构呈类十字形破坏分布，纵向受力板变形量随无量纲数ph/σcrl的增加而增加，随壁板厚度的增加而减少，此阶段纵向受力板在压力载荷作用下主要表现为弯曲变形；当载荷进一步增大(ph/σcrl＞ 0.004 7 )时，多箱型结构呈圆形破坏分布，纵向受力板被炸飞或压扁，没有具体测量其变形量.

图14 无量纲数的纵向受力板破坏程度分布图Fig.14 Damage degree of dimensionless longitudinal plates

3.4 分析方法实验验证

使用上述方法对文献中的3 组实验进行分析.实验1：文献[14]进行了舰船缩比模型内爆实验，每个箱室尺寸(长×宽×高）为0.15 m×0.125 m×0.1 m，壁板厚度为3 mm，材料屈服强度为464 MPa，断裂应变为0.3，将0.05 kg 的TNT 炸药置于箱室内引爆，多箱型结构失效特征如图15 所示.

图15 多箱型结构内部爆炸失效特征[14]Fig.15 Failure characteristics of multi-box structure subjected to internal explosion[14]

实验2：文献[14]中进行了多层舰船结构舱内爆炸试验，5 kg TNT 药包置于中间舱室中心起爆，舰船结构层高0.6 m，每个箱室长0.35 m，宽度方向为0.4 m，壁板厚度为3 mm，材料屈服强度为552 MPa，断裂应变为0.3，最底层隔板经过特殊加强处理.船舱内部破坏情况及横截面方向破坏示意图如图16 所示.

图16 多箱室结构模型内部爆炸实验[14]Fig.16 Experiment of ship model subjected to internal explosion[14]

实验3：文献[36]中进行了大尺度多箱型结构模型内部爆炸实验，实验模型为三层多箱室结构，顶部带有附属结构，层高0.6 m，沿Y-Z方向可分3 个箱段，包含三道主纵隔板以及若干次纵隔板，每个箱段长2.3 m，宽度方向为2.9 m.结构模型中不同结构单元所用钢材不同，01 水平板为4 mm 厚的Q420 钢板，其余水平板和纵隔板为2 mm 厚的Q235 钢板，各钢材力学性能参数如表5 所示.将2 kg 的TNT 炸药放置在01 和02 水平板中间位置，炸药密度1 500 kg/m3.内部爆炸发生后，模型整体破坏情况如图17(a)所示，其横截面方向模型内部破坏示意图如图17(b)所示.

表5 各钢材力学性能参数Tab.5 Mechanical properties of each steel parameters

图17 多箱室结构模型内部爆炸实验[36]Fig.17 Experiment of multi-chamber structure model subjected to internal explosion[36]

计算炸药总内能，针对各向异性箱型结构，根据受载有效面积占比分配能量.在破坏范围分析中，利用式（11）计算各壁面破坏临界值，代入式（10）计算壁板断裂能，计算无量纲数W/UP，根据离散突变破坏规律，得到破坏壁面数.在破坏分布模式分析中，分别用式（4）、（5）计算压力P和式（14）计算纵向受力板屈服强度，代入参数计算无量纲数 (ph)/(σcrl)，参照图13 分析破坏分布模式，对照实验1 和2 的计算结果与实验结果如表6 所示.

表6 对照实验的计算与实验结果Tab.6 Calculations and experimental results of the control experiment

在对照实验1 破坏范围分析中，由于未考虑箱型结构棱边焊接方式和炸药放置位置，在X-Y横向受力板破坏数分析中存在些许误差.破坏分布模式分析中，黄色、红色壁面大挠度变形，绿色壁面无明显变形，Z-Y方向整体呈十字形破坏相符.在对照实验2 中，X-Y方向横向受力板破坏数稍有偏差，因为舰船最底层隔板经过特殊加强，模型X-Y方向横向受力全部破损，与计算评估基本一致.破坏分布模式分析中，X-Y和X-Z纵向受力板均被炸飞，与计算结果相符，整体呈现圆形破坏模式.在对照实验3 中，02 和03 水平板均发生严重塑性变形或被炸飞，X-Z方向横向受力板破坏数为3，与计算结果相符.在破坏分布模式分析中，X-Y纵向受力板未存在明显变形，X-Z纵向受力板几乎均被压弯或炸飞，与计算评估基本一致.使用以上分析方法能够较好地预测多箱型结构在内部爆炸作用下的破坏范围和毁伤模式.

4 结 论

针对多箱型结构内部爆炸的破坏威胁研究其破坏模式和破坏分布，开展了基于内部爆炸载荷和结构响应的毁伤效果与分析方法研究.主要结论如下.

（1）研究了结构几何尺寸、强度与爆炸载荷对整体破坏模式的影响，发现随着爆炸能量的增加，以爆炸当舱为中心，破坏模式逐层从十字形向类十字形再向圆形破坏转化，破坏范围逐层向外扩展.通过增加箱型结构的壁厚，能够有效减小破坏范围和降低破坏程度.

（2）针对各向异性多箱型结构提出等效结构强度 σ，结合等效结构强度和爆炸成形能量准则，提出多箱型结构发生内部爆炸后破坏箱室数和破坏壁面数的分析方法和相应的无量纲数.研究发现，虽然无量纲数P/σ和W/UP是连续的，但是破坏箱室数和壁面数是阶跃的，只有大于该阶段破坏阈值，才能到达下一层箱室或者壁板.

（3）根据纵向受力板破坏程度区分多箱型结构整体破坏模式，提出能描述整体破坏模式的分析方法和无量纲数，并详细分析了纵向受力板变形量与无量纲数Ph/ σcrl和破坏模式之间的变化规律.使用破坏模式图，将爆炸工况参数代入，能够快速预测二维多箱型结构大致破坏情况，并提出进一步推导至三维方法.最后通过已有实验验证了所提出的预测方法，结果一致性良好.该方法能够有效提高舰船等多箱型结构内部爆炸毁伤效能预测的能力和效率，为其破坏预测和防护设计提供参考.